粉土与粉质黏土互层中静压桩桩土界面径向土压力研究

王永洪，马加骁，张明义，桑松魁，白晓宇，杨苏春

（1.青岛理工大学土木工程学院，山东青岛，266033；2.山东省高等学校蓝色经济区工程建设与安全协同创新中心，山东青岛，266033）

目前，静压桩桩土界面处土体抗剪强度的研究已成为诸多学者关注的焦点[1-4]。同时，学者们也对静压桩贯入过程中桩周土体塑性区和弹性区中引起的总径向土压力和孔隙水压力变化规律进行了研究，但桩土界面处土体相比桩周塑性区和弹性区土体产生更大的径向位移，土体强度处于极限破坏状态，受力状态与塑性区和弹性区不同，所以，桩土界面总径向土压力有待深入研究。目前，主要通过试验和理论2种手段对总径向土压力进行研究。

试验研究主要通过现场试验和室内模型试验2种方式进行分析。人们在桩周不同深度处和距离桩不同间距处埋设土压力传感器，分析桩端贯入不同测量面处土压力的变化规律[5-7]。唐世栋等[8]在桩周埋设土压力传感器，探讨了单桩贯入过程中对周围土体中产生侧压力增量的变化规律和分布情况。张忠苗等[9]将土压力传感器安装于桩端，通过现场静压开口管桩，分析了贯入过程中桩周土体中土压力的分布情况，发现桩周土体中的总径向土压力随贯入深度呈先增大后减小的趋势。DOHERTY等[10]通过在黏性土中静压开口管桩和闭口管桩的现场试验，分析了贯入过程中不同桩端形式对桩侧总径向土压力和孔隙水压力的分布特征的影响。陆烨等[11]通过室内模型试验研究了砂土中静压桩的沉桩过程，基于DIC 技术对桩周土体位移与相应的土压力变化规律进行分析。张宇超等[12]将土压力盒埋设于桩身周围，开展了室内模型试验，探讨了沉桩过程引起的径向土压力的变化规律，并且发现锤击沉桩和静压沉桩引起的变化规律相似。以上研究均是对桩周土体在径向方向桩侧土压力进行探讨，但未考虑随桩身贯入不同深度处桩土界面总径向土压力的变化规律。李雨浓等[13]采用离心原理，开展了不同离心场下的模型试验，用模型桩嵌入式安装土压力传感器测量径向压力，认为桩端的相对高度对径向压力的发展有较大影响，桩侧总径向土压力存在退化现象，试验仅对均质黏土中桩侧总径向土压力进行探讨，而未对层状土中桩侧总径向土压力随贯入深度的变化规律进行分析。

理论研究主要依据球（圆）孔扩张理论，将沉桩过程模拟成一系列球孔的连续扩张，分析静压桩贯入过程中桩周土体中径向土压力和孔隙水压力增量的变化规律[15-17]。李镜培等[18]开展了饱和黏性土中静压沉桩离心模型试验，并结合球孔扩张理论，通过模型试验和理论对比分析，获得了静压桩贯入过程中总径向土压力的变化规律。李林等[19]基于柱孔扩张理论，考虑K0固结特性和应力历史因素推导出了K0固结饱和黏性土中柱孔扩张弹塑性解，但只考虑了孔周应力随径向的变化规律，而未解答随深度分布的规律。张亚国等[20]通过开展离心模型试验以及对已有的圆孔扩张理论进行修正，提出了相应的沉桩挤土模型，试验表明桩周土体总应力和超孔压变化主要由距桩的水平距离和埋深控制。LI等[21]基于修正的剑桥模型，考虑到圆孔扩张周围土体的三维力学特性，采用变化应力张量法推导出了基于SMP 准则的圆孔不排水扩张的近似解析解，但仅能分析孔周应力随径向的变化规律。张鹏远等[22]通过球孔塑性区土体的受力特征，得到了饱和黏性土中球孔扩张问题的屈服准则，利用该准则得出了饱和土体球孔扩桩问题的总应力场，并结合有效应力原理推导出了有效应力场。可见，人们通过理论研究探讨了桩周土体中不同区域内总径向土压力的分布规律，但未考虑沉桩过程中桩土界面剪切引起的总径向土压力退化问题，同时，沉桩过程中不同深度处桩土界面总径向土压力随贯入深度的变化规律也有待进一步探究。

综上所述，目前对黏性土中静压桩沉桩过程桩周土体总径向土压力的研究中，主要通过理论以及易于控制变量的室内模型试验对桩土相互作用进行研究；已有现场试验大多将传感器埋置于桩周土体中，而桩土界面处的土压力和桩周的土压力存在较大差异。现有研究主要分析了桩周土体塑性区和弹性区内径向土压力的变化规律，探讨了桩侧总径向土压力沿径向方向上的分布规律，而对桩土界面处桩侧总径向土压力沿深度上的变化规律探讨较少。

为此，本文作者在PHC 管桩桩身安装硅压阻式土压力传感器，进行静压桩沉桩过程现场试验，探讨贯入过程中桩土界面处桩侧总径向土压力的变化规律，对沉桩过程中桩土界面处桩侧总径向土压力沿深度方向上的变化规律进行分析，揭示层状土中静压桩贯入过程中桩土界面受力特性。同时，采用土的极限平衡理论与现场试验相结合的手段对静压桩贯入过程中桩土界面总径向土压力进行探讨，从理论上分析桩土界面受力特性。研究结果可为工程中静压桩贯入特性以及承载能力的分析和预估提供参考。

1 试验方案

1.1 工程概况

试验场地位于山东东营市河口区湖滨路以西、河兴路以北。地貌单元属于黄河三角洲冲积平原地貌，表层覆盖厚度为0.9～5.3 m 的回填土，场地内主要分布粉质黏土层和粉土层。地下水位埋深为0.30～3.00 m。根据现场勘探揭露，场地土层分布情况如表1所示。

表1 土层性质参数表Table 1 Soil property parameter table

1.2 试验设置

试验采用PHC-A400（95）型预应力混凝土管桩作为试验桩，桩长为12 m。采用硅压阻式土压力传感器监测沉桩过程中桩土界面处总径向土压力，其主要性能指标如表2所示。试验桩上设置6个测量断面，从桩端分别按照1D，2D，4D，8D和12D（D为桩身直径，D=40 cm）的间距分布，传感器布置示意图见图1。桩端处传感器的中心距桩端的距离为0.5D，从而避免了桩端端头板对传感器的影响。

表2 硅压阻式传感器性能指标Table 2 Performance indicators of silicon piezoresistive sensor

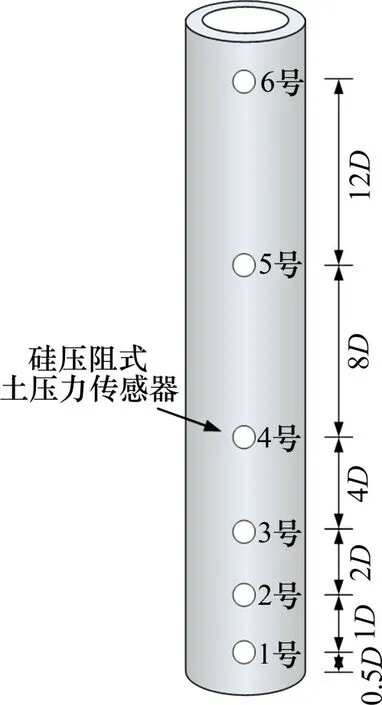
图1 传感器安装示意图Fig.1 Sensor installation diagram

传感器安装之前，首先在桩身定位，然后用开孔器在桩身上开传感器安装孔，在开孔时首先用12 mm 的开孔器将桩壁钻透，再用直径为20 mm的开孔器进行扩孔，深度为20 mm，在孔内形成台状。开孔完毕之后，按照孔洞位置布置传感器，其后在传感器四周和孔壁四周涂抹环氧树脂胶将其固定在桩身表面，同时控制传感器的高度与桩表面齐平。为提高环氧树脂胶的黏结强度，需等待环氧树脂胶固化24 h，不得过早沉桩。此外，试验之前，所采用传感器均经过精确标定。

压桩机械采用680 t 液压静力压桩机，最大行程为1.8 m，沉桩速度为1.8～3.0 m/min。在每个行程开始前均用水平尺测量桩身的垂直度，确保压桩过程中桩身垂直贯入土体，从而提高测量数据的精确度。本次试验贯入速度较慢且在每个行程中均以恒定速度贯入，与锤击打入桩相比，此次贯入属于稳态贯入，所以，沉桩过程中不考虑压桩力对桩身的冲击作用。在沉桩过程中，以桩长作为终压控制标准。

选用CF3820 高速静态信号测试分析仪读取测量数据，可实现6通道同时动态采集，采集频率为100 Hz。

2 试验结果与分析

2.1 桩土界面总径向土压力

通过对试验桩PJ1桩身安装的硅压阻式土压力传感器监测数据以及贯入过程中传感器的入土深度，绘制出沉桩过程中桩土界面处桩侧总径向土压力随传感器入土深度的变化曲线，如图2所示。

图2 桩侧总径向土压力随传感器入土深度变化曲线Fig.2 Variation curves of total radial earth pressure on pile side with depth of sensor

由图2可以看出：随贯入深度逐渐增加，1～6号传感器的桩侧总径向土压力逐渐增大，增大幅度随土层的变化而变化；在粉质黏土夹层与粉质黏土层交界处，1 号与2 号传感器所测总径向土压力出现突增的现象，且1号传感器测得的总径向土压力突增最明显，在10.7 m 时其增幅为43.37%，而2～6号传感器土压力突增现象逐渐减弱，总径向土压力逐渐减小。这是因为：1）粉土密实性较好，桩在粉土层贯入时，桩身与土体紧密接触，使传感器刚贯入粉土层时出现压力突增现象。2）1号传感器靠近桩端，所测总径向土压力为桩端刚刚破土时产生的总径向土压力，而2～6号传感器所测的总径向土压力为经过了不同剪切距离之后的压力，剪切距离越大，桩身与土体之间的接触越不密实，产生的应力释放越多，从而压力突增现象逐渐减弱。当各传感器由粉土层贯入粉质黏土层时，各传感器的总径向土压力出现减小的趋势，以1号传感器为例，当贯入深度为3.9 m时，总径向土压力由145.7 kN减小到135.9 kN，并且在粉质黏土层中贯入时总径向土压力增幅较小。这是因为与粉土相比，粉质黏土的密实性较差，桩身与粉质黏土之间接触远比桩身与粉土之间的紧密程度小，从而使总径向土压力减小。

从以上分析可以看出：总径向土压力的变化与土层性质有关，当桩身由软土层（粉质黏土）贯入硬土层（粉土）时，桩侧总径向土压力出现突增现象；当桩身由硬土层（粉土）贯入软土层（粉质黏土）时，桩侧总径向土压力出现减小趋势，这与李雨浓等[14]的研究结果相符。由此可知，桩侧总径向土压力与土的软硬程度密切相关。

2.2 不同土层桩土界面总径向土压力退化效应

由图2可知：随桩身贯入，在同一深度处的桩侧总径向土压力逐渐减小，距桩端越远的传感器在同一贯入深度处测得的桩侧总径向土压力减小，这与LEHANE等[23-24]的研究结果一致。侧摩阻力的形成机理也进一步验证了桩侧摩阻力的退化现象。可以看出，在预估或计算沉桩过程中桩侧摩阻力时，为避免估算值过大，应考虑桩的长度效应。

根据试验所得的总径向土压力，可以得到不同土层中相邻两传感器之间桩侧总径向土压力的平均退化幅度，如图3所示。

图3 各土层相邻传感器总径向压力平均退化幅度Fig.3 Average radial deformation degradation of adjacent sensors in each soil layer

由图3可以看出：1～2 号传感器之间总径向土压力的平均退化幅度最大，最大退化幅度约为32.01%。而其他传感器之间的退化幅度较小，退化幅度为0～8%。这表明沉桩过程中桩端破土之后，初始剪切破坏对总径向土压力的应力释放和总径向土压力的退化影响最大，此时，总径向土压力的退化现象最明显。之后，随桩身贯入，桩土界面土体为重塑土，强度大幅降低，在桩土界面不断发生剪切情况下，总径向土压力不断减小，但桩土界面重塑土的强度逐渐减低，退化幅度也逐渐减小。由此可知，同一深度处，在沉桩初期，桩侧总径向土压力退化较明显，而随桩身的不断贯入，退化幅度减小。这与李雨浓等[13]所得结果一致。

经过进一步分析，硬土层（粉土层）的总径向土压力退化幅度明显比软土层（粉质黏土）的大，退化幅度最大相差14.22%。这说明在桩土界面不断发生剪切作用下，硬土层比软土层更容易使总径向土压力退化，这是因为软土层土质较软，在上覆土重的作用下，桩土界面不断发生剪切作用，软土与桩身接触较紧密，而在硬土层中，土体的自立性较软土层强。在桩体贯入过程中，桩身对桩周硬土层不断施加剪切作用，同一深度处硬土层与桩身之间的接触程度逐渐降低，所以，硬土层中总径向土压力退化幅度明显比软土层中的幅度大。其中粉质黏土（夹）的总径向土压力变化规律与其他土层的变化规律不同，主要是本层为夹层土性的不确定因素较多，使本层的总径向土压力变化规律不明显。

3 桩土界面径向土压力理论分析

球（圆）孔扩桩理论适用于分析桩侧径向土压力随水平距离的变化规律，而无法反映随沉桩的进行桩侧径向土压力沿深度方向的变化，即不能展现深度变化对桩侧径向土压力的影响。在桩身贯入过程中，靠近桩身的土体发生塑性（破坏）变形和较大位移，鉴于此，桩土界面处的径向土压力可根据极限平衡理论进行分析。将土体视为服从Mohr-Coulomb 屈服准则的理想弹塑性土体。在沉桩之前，土体单元的最大主应力为上覆土体自重应力σz=∑γh，最小主应力为侧压力στ=K0∑γh。沉桩结束后，由于桩身的挤土作用桩身附近土体发生较大的水平位移，土体强度达到极限，此时，土体单元的最大主应力为侧向压力，最小主应力为竖向应力。根据土体的极限平衡理论以及应力圆可得出沉桩前后土体应力的变化[25]，如图4所示，图4中，σ1为最大主应力，σ3为最小主应力。

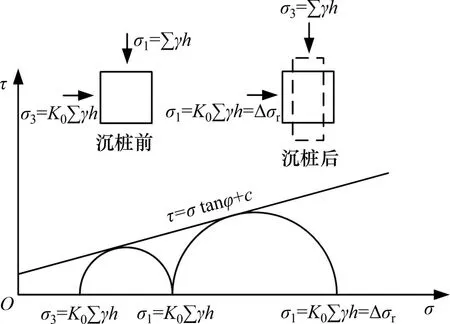
图4 土体单元应力圆应力变化Fig.4 Stress variation of soil unit stress circle

由极限平衡理论的桩侧土压力随深度的变化规律，可知总径向土压力σr和上覆土体自重应力σz分别为

式中：γ为土体重度；h为土层厚度；φ为土的内摩擦角；c为土的黏聚力。

3.1 桩土界面总径向土压力试验结果与理论计算值比较

通过极限平衡理论以及根据式（1）和现场工程勘察报告提供的各土层物理参数，计算得到桩土界面总径向土压力随贯入深度的变化。1号传感器位于桩端，所测的径向土压力为桩端刚破土时的桩侧总径向土压力。所以，采用桩端1号传感器测得的总径向土压力与极限平衡理论计算值进行对比，结果如图5所示。

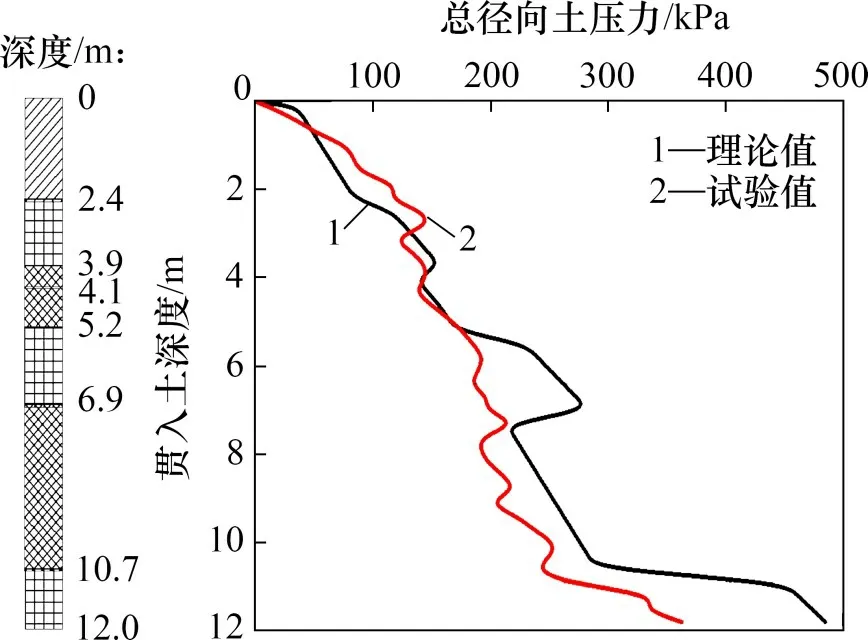
图5 总径向土压力与理论值对比Fig.5 Total radial earth pressure value versus theoretical value

由图5可以看出：在贯入初期，试验值随贯入深度的增幅比理论计算值的增幅大，这主要是现场试验中由于压桩机的自身重力较大，在地表产生较大的附加荷载，从而使贯入初期试验值略大，压装机械的自身重力对桩侧总径向土压力的影响深度为2～3 m。在同层土中，总径向土压力的理论计算值随深度增加近似呈线性增长，而现场实测曲线即使在同层土中总径向土压力随深度增加出现细小增长。这是因为在进行理论计算时，同层土中的各参数取值相同；而现场土压力的实测曲线受现场土层局部不均匀等因素的影响，相同土层中总径向土压力存在一定的波动，但这并不影响整体规律的分析和研究。

在粉质黏土层，桩侧总径向压力试验值与理论计算值变化规律吻合较好，而在粉土层理论计算值与试验值存在一定的偏差。当贯入深度为6.4 m 时，总径向土压力理论计算值为284.08 kN，总径向土压力试验值为183.51 kN，理论计算值约为试验值的1.55 倍；在10.9 m 时，总径向土压力理论计算值为450.07 kN，总径向土压力试验值为262.70 kN，理论计算值约为试验值的1.71 倍。这是因为粉土的渗透性较大，当桩端在粉土层破土贯入时极易形成孔隙水消散通道，这与张忠苗等[9]研究的结果一致。而采用极限平衡理论计算总径向压力时未考虑孔隙水的消散，致使在粉土层时理论计算值与试验值存在偏差。粉质黏土中由于土的渗透性较小，孔隙水较难消散，所以，在粉质黏土层理论计算值与试验值吻合较好。

从整体的曲线变化趋势可以看出，极限平衡理论计算值与现场实测值变化规律基本一致，可以采用极限平衡理论分析桩侧总径向土压力沿深度方向的变化规律[25]。

3.2 考虑孔隙水消散的桩土界面总径向土压力理论计算方法

由3.1 中分析可知，由于粉土的渗透性较大，易使孔隙水消散，致使现场实测的总径向土压力增幅比理论值的增幅小。现将1号传感器贯入⑤和⑦粉土层时的实测值与极限平衡理论计算值进行对比，见表3。因为②粉土层受压装机自重等多种因素的影响，故本次只对⑤和⑦粉土层进行分析。

表3 粉土层中实测值与理论计算值的比较Table 3 Comparisons of measured values and theoretical calculations in silty soil

由表3可知：当桩身贯入⑤和⑦粉土层时，桩土界面处总径向土压力实测值分别是理论计算值的69.07%～80.76%和66.28%～82.33%。从图5可知粉土的透水性大，孔隙水易消散。由于⑤和⑦土层的孔隙比相近，在⑤和⑦粉土层中超孔压消散的幅度基本相同。

将桩土界面总径向土压力实测值与极限平衡理论计算值之比称为超孔压消散系数。粉土中孔隙水的消散对总径向土压力的影响较大，根据以上分析，可以将式（1）修正为

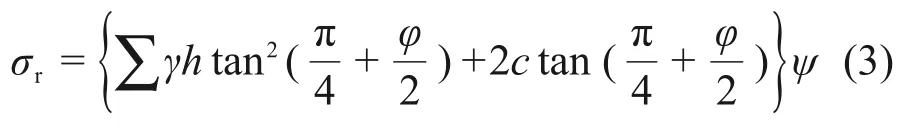
式中：ψ为超孔压消散系数（土层位于水位线以上时取1），取值范围为0.7～0.8。

黏土中总径向土压力为

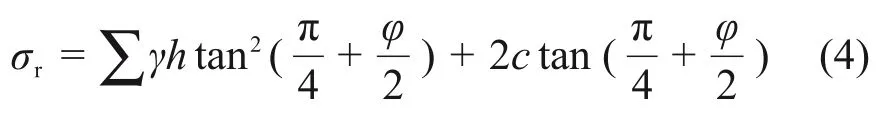
经超孔压消散系数修正之后的极限平衡理论计算值与现场实测值对比，如图6所示。

图6 总径向土压力实测值与理论修正值对比Fig.6 Comparison of measured values and theoretical corrections of total radial earth pressure

从图6可以看出：考虑了孔隙水消散的极限平衡理论修正后公式得到的沉桩过程中桩土界面总径向土压力随贯入深度的变化规律与现场实测值变化规律极其相似。在粉质黏土层，总径向土压力现场实测值比理论计算值略小，理论值约为实测值的1.1倍，说明在黏土层也存在孔隙水小幅度消散，但实测值与理论计算值相差较小，并不影响整体规律的研究。以上分析表明，采用考虑了孔隙水消散修正后的极限平衡理论公式适合用于分析或估算粉土与粉质黏土互层中桩端刚刚破土时桩土界面总径向土压力。

3.3 同时考虑孔隙水消散和剪切破坏桩土界面总径向土压力退化的理论计算方法

在静压桩贯入过程中，桩土之间不断发生剪切作用，桩土界面不断产生应力释放。由图2可知，不同位置传感器贯入同一深度时，径向土压力出现了明显的退化现象。目前，当采用球（圆）孔理论或极限平衡理论公式计算或估算沉桩过程中桩土界面总径向土压力时，均未考虑贯入过程中径向土压力的退化现象即桩长效应，这必然会使桩土界面总径向土压力偏大。

沉桩过程中桩土界面不断发生剪切破坏，由于土性不同土的物理参数不同，桩土界面也展现出不同的总径向土压力退化型式。本文计算了桩身不同位置即不同H/D（H为测量面距桩端的距离；D为桩身直径）处传感器分别在粉土和黏土层中贯入过程中的实测值ps与极限平衡理论计算值pu比值的均值η。η表征不同位置传感器分别贯入粉土层和粉质黏土层时总径向土压力的退化程度，称为剪切退化程度参数。将粉土和黏性土中的剪切退化程度参数η通过拟合分别建立了与H/D的关系式，如图7所示。

由图7可见：黏土和粉土中桩土界面处总径向压力的剪切退化程度参数随桩土界面的不同剪切距离（剪切程度不同），均呈幂函数关系[26]。土性不同退化系数也不同，在黏土中剪切退化系数为0.12，在粉土中剪切退化系数为0.19。这表明在粉土中随桩身的贯入桩土界面处总径向土压力的退化幅度比黏性土中的退化幅度大，这与现场试验中各传感器之间得到的总径向土压力退化规律一致。

图7 η随H/D的变化Fig.7 Variations of η with H/D

依据黏土中和粉土中退化程度参数关系式对总径向土压力的极限平衡理论计算公式进行二次修正。计算公式考虑到桩土界面循环剪切作用引起的桩侧总径向土压力的退化效应，得到在不同剪切程度下总径向土压力的极限平衡理论计算公式，将式（3）和式（4）进行二次修正。

粉土中桩侧总径向土压力在不同剪切程度下的计算公式为

式中：η=0.77（H/D）-0.12。

黏土中桩侧总径向土压力在不同剪切程度下的计算公式为

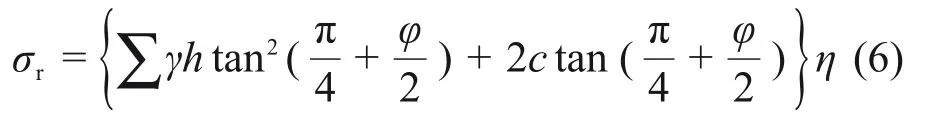
式中：η=0.75（H/D）-0.19。

根据式（5）和式（6），可得到与现场试验相应传感器贯入过程中桩土界面总径向土压力。图8所示为桩侧总径向土压力分别与极限平衡理论公式二次修正前后对比曲线。

由图8可以看出：未考虑剪切破坏对总径向土压力退化的影响时，桩土界面总径向土压力实测值与理论计算值相差较大，在沉桩结束时，2～5号传感器桩土界面总径向土压力实测值与相应深度处理论计算值的比值分别为74.94%，67.11%，61.87%和53.81%。这说明桩身贯入时桩土界面剪切破坏对总径向土压力的影响较大，在估算贯入过程中不同深度处桩侧总径向土压力时，桩土界面剪切破坏不容忽视。同时，考虑了孔隙水消散和剪切破坏引起总径向土压力退化的理论修正值与现场实测值吻合度较高，两者的变化规律和数值基本相同。这说明采用极限平衡理论对贯入过程中不同位置处的桩侧总径向土压力进行估算时，若不考虑贯入过程中径向土压力的退化现象，即桩长效应，必然会使桩侧总径向土压力偏大。采用修正后的公式提高了对沉桩过程中桩土界面总径向土压力估算的准确性，从而也对静压桩沉桩过程中桩侧摩阻力的预估更加准确，这提高了对静压桩压桩力和沉桩结束后承载力估算的准确性。

图8 桩侧总径向土压力实测值与理论值对比图Fig.8 Comparisons of measured and theoretical values of total radial earth pressure on pile side

4 结论

1）沉桩过程中引起的总径向土压力随贯入深度增加逐渐增大。当桩身由软土层贯入硬土层时，桩侧总径向土压力出现突增现象；当桩身由硬土层贯入软土层时，桩侧总径向土压力呈减小趋势，这说明桩侧总径向土压力与土层性质密切相关。

2）在沉桩过程中同一贯入深度，随桩身的贯入，桩侧总径向土压力存在明显的退化现象。在沉桩初期，同一深度下桩侧总径向土压力退化最明显，而随着桩身的不断贯入，退化现象变得越来越不明显。桩侧总径向土压力在硬土层的退化幅度比在软土层的退化幅度大。

3）极限平衡理论适合分析桩端处总径向土压力沿深度方向上的变化规律。在粉土中计算桩土界面总径向土压力时，需考虑孔隙水消散的影响，进行超孔压消散系数的修正，超孔压消散系数为0.7～0.8。

4）当采用极限平衡理论分析沿桩长方向不同深度的总径向土压力时，在粉土中需同时考虑孔隙水消散和不同剪切程度（H/D）对径向土压力退化的影响，剪切退化系数为0.19；在粉质黏土中考虑不同剪切程度（H/D）对径向土压力退化的影响，剪切退化系数为0.12。极限平衡理论公式经过二次修正后桩侧总径向土压力计算值与试验值相吻合。所以，在采用极限平衡理论计算桩侧总径向土压力时，应考虑桩长效应，以免对桩侧总径向土压力估算过大。