足尺装配式混凝土异形柱框架结构抗震性能试验研究

倪韦斌，王少杰，乔德浩，吕绪亮，周满，赵立滨

（1.山东农业大学水利土木工程学院，山东泰安，271018；2.山东明睿达新技术研究院有限公司，山东济南，250101；3.中南大学土木工程学院，湖南长沙，410083）

异形柱结构柱楞在室内不突出、美观适用，能获得较好的建筑功能并减轻结构自身重力[1]；装配式建筑是我国建筑业发展的重要方向之一[2-3]，以混凝土结构为例，可通过工厂预制大幅减少现场湿作业，具有节能环保、现场装配、建造高效等特点，已得到广泛应用。新民居建设利于提升农村居民居住和生活质量，是实施乡村振兴国家战略的重要组成部分，采用装配式混凝土异形柱框架结构建设新民居易被接收和推广[4]。然而，由于JGJ 149—2017“混凝土异形柱结构技术规程”[5]尚没有关于装配式混凝土异形柱框架结构抗震设计的有关规定，加之异形柱截面的特殊性，因此，以新民居的研发与示范建设为背景开展装配式混凝土异形柱框架结构的抗震性能研究十分必要。

关于T型、L型及十字型等异形柱构件与节点的静力与抗震性能已取得诸多成果[6-12]，如王欣等[13]对采用灌浆套筒和直螺纹套筒2种连接方式的装配式异形柱节点抗震性能开展了拟静力试验；韩明杰等[14-15]针对浆锚连接预制装配式异形柱框架梁柱节点的抗震性能开展了试验与数值研究。在异形柱框架结构体系的抗震性能研究领域，大多以现浇钢筋混凝土结构[16-17]、型钢混凝土异形柱框架结构[18-20]等为主，而针对装配式混凝土异形柱框架结构的抗震性能研究成果较少。

为此，本文作者以真实工程为背景，设计并制作二层二跨装配式混凝土异形柱框架结构足尺模型，对其进行低周往复荷载试验并开展静力弹塑性分析简化方法研究，旨在为装配式混凝土异形柱框架结构的推广尤其是在新民居体系中的应用提供参考依据和方法支持。

1 试验概况

1.1 模型设计与拆分

以装配式新民居的研发与示范工程建设为背景，选取进深方向二层二跨足尺单榀框架开展低周往复荷载试验，研究装配式混凝土异形柱框架结构的抗震性能。模型设计与拆分方案如图1所示。进深方向上部结构长7.1 m（左右两跨净跨分别为3.7 m和2.0 m），两端和中间分别为T型和I型截面柱。在加载方向，其截面高度分别为500 mm和400 mm，肢厚为200 mm，端部T 型柱翼缘宽为600 mm；一、二层层高分别为3.26 m 和3.00 m，框架梁高均为400 mm。模型采用“浆锚连接+节点后浇”方案，分层拆分包括T 型截面柱4 根（C-ST1，C-NT1，C-ST2 和C-NT2）、I 型截面柱2根（C-MI1和C-MI2）及梁2根，共8个预制构件。梁柱截面配筋如图2所示，纵筋均采用HRB400、箍筋为HPB300，预制构件混凝土强度等级为C30，节点采用C35强度等级的细石混凝土。下侧垫梁长为9.0 m，截面长×宽为800 mm×450 mm，预留出筋长度为700 mm（预留钢筋直径的35倍）。

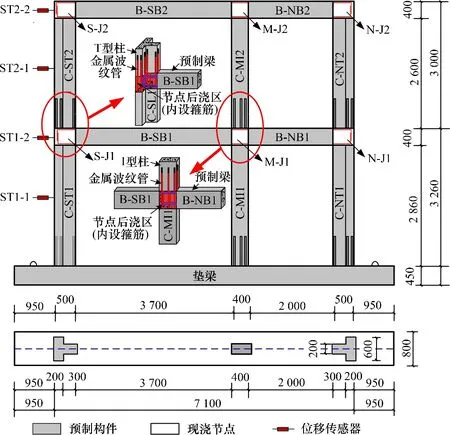
图1 模型设计与拆分Fig.1 Design and separation of specimen

1.2 构件预制与模型装配

框架梁、框架柱均在天齐明达装配式建筑产业园预制，预制柱钢筋笼下端绑扎700 mm长金属波纹管作为浆锚连接搭接孔道，浇筑混凝土前在各预制构件内按图2所示方案预埋应变测点；构件采用室内洒水自然养护28 d 后，吊装转运至结构试验大厅与同期预制的垫梁装配成整体。图3所示为二层二跨装配式混凝土异形柱框架结构的装配流程，首先将一层预制T型和I型截面柱装配至垫梁上，并采用斜撑调直固定后对柱根部区域封边，待封边24 h 即封边料满足强度要求时，采用压力注浆注入水泥基灌浆料，待各预留注浆孔都均匀流出注浆料并完成封堵，待一层注浆24 h 时吊装一层框架梁，节点区采用C35细石混凝土浇筑；之后，按照与一层装配相同的方法装配二层预制柱、预制梁。装配完成后的模型如图3（c）所示，待节点区后浇混凝土回弹与同条件留样强度均达到C35后进行加载。

图3 模型装配Fig.3 Assembly of model

1.3 试验加载与数据采集

在一、二层框架梁对应高度处分别采用MTS加载系统控制作动器按倒三角形施加低周往复荷载[21]，开裂前采用力控制、开裂后采用位移控制，加载制度如图4所示。具体而言，开裂前以二层作动器为基准，水平出力以10 kN为第1加载步和级差加载至试件开裂；然后，将开裂位移取整（10 mm）并按其整数倍进行位移控制加载，每级循环3次，至试件承载力下降至峰值荷载的85%时结束加载。加载前，通过水平拉杆和刚性夹板将模型与MTS 作动器紧固；垫梁竖向通过刚性压梁、长螺杆与反力墙台座紧固，水平向通过在垫梁两端设置螺旋千斤顶止推限位，以保证加载全过程模型不翘起、不滑移。

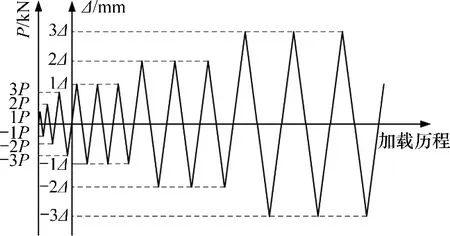
图4 加载制度Fig.4 Loading system

加载期间主要采集抗侧承载力、侧向变形、钢筋与混凝土的应变、裂缝演化等，其中MTS 作动器可全程自行采集出力与变形信息。如图1所示，通过沿框架高度方向布置的位移传感器采集框架侧向变形；在梁柱节点区、浆锚连接区对应纵筋、箍筋及混凝土构件的表面布置大量应变测点，部分应变测点布置位置如图2所示。应变与位移传感器的数据通过UT8516动静态应变采集分析系统同步采集。安排多人分区全程观察并记录试验现象，主要包括裂缝出现、发展情况及混凝土压碎、节点区出铰信息等，缝宽通过ZBL-F103裂缝宽度观测仪测试。

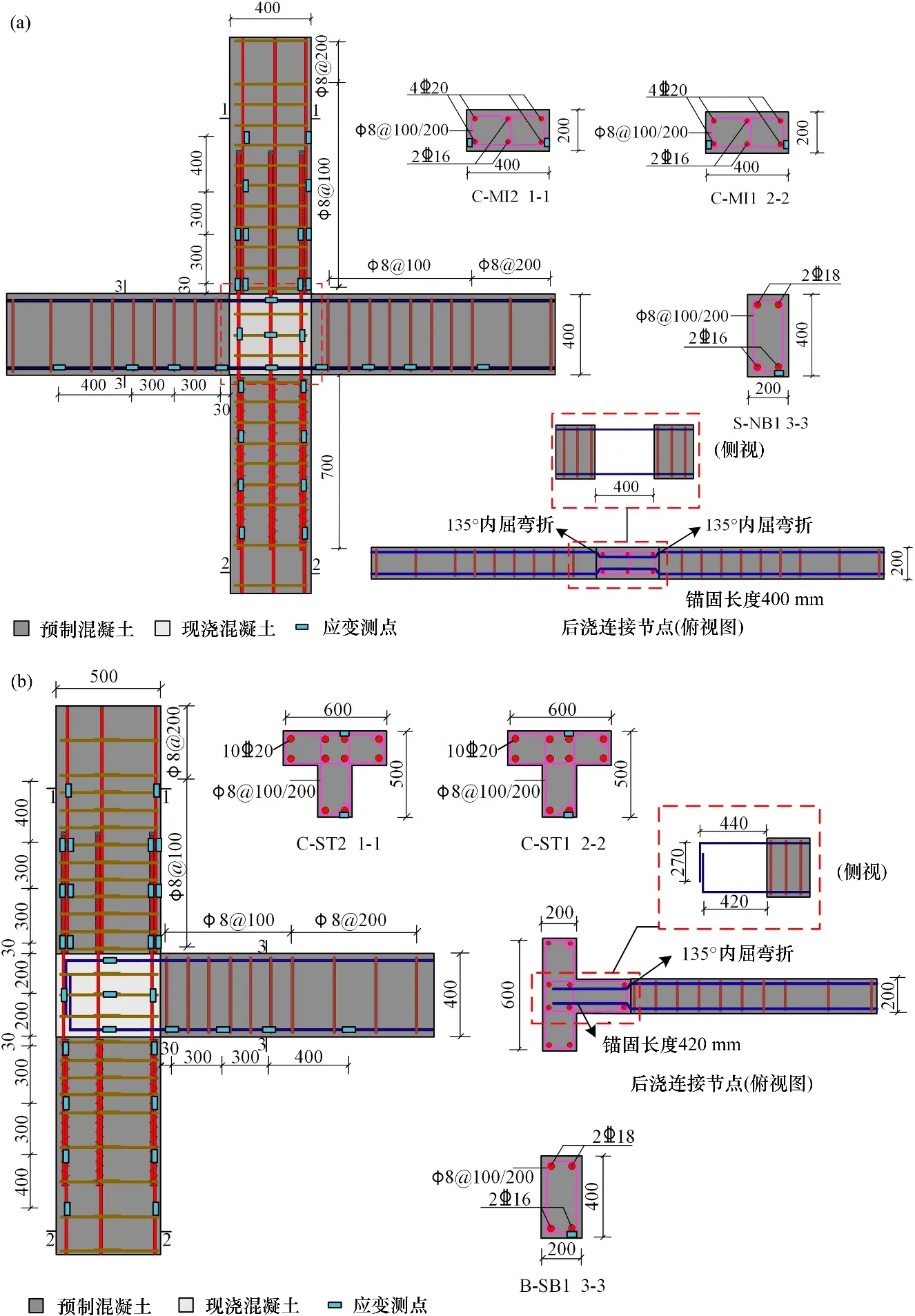
图2 配筋与测点预埋Fig.2 Reinforcement and embedding of measuring points

2 试验现象与失效状态

2.1 试验现象

由于加载试件为二层二跨足尺模型，为清晰描述试验现象，定义各层层间位移角θi，即

式中：i为楼层号，i=1或2；Δi为第i层层间位移；Hi为第i层层高。H1对应一层加载点中心至垫梁顶的高度，H2取两作动器对应加载点形心之间的距离，分别为3.06 m 和3.00 m。试验现象如图5所示。

图5 试验现象Fig.5 Experimental phenomenon

在试验伊始力加载阶段，当θ2=1/696时，在节点M-J2 下侧，即二层柱C-MI2 顶部结合面处出现首条水平接缝裂缝；随后，在节点S-J1与梁B-SB1端部结合面处出现竖向接缝裂缝，裂缝由梁底向梁顶发展。当θ1=1/424 时，在一层柱C-NT1 的柱脚浆锚灌浆口处出现首条构件裂缝，呈水平走向，缝宽0.16 mm，此后，由力加载阶段转为位移加载阶段。

位移加载阶段，当θ2=1/300 时，节点M-J2 下侧水平接缝裂缝贯通；当θ1=1/151时，二层梁两端出现竖向拼接裂缝，一层各柱在距离垫梁顶部1.2 m 高度范围内，各柱出现数条水平贯通裂缝。当θ1=1/101时，梁体各端部区域数条竖向裂缝显现（见图5），裂缝最宽处为0.3 mm；同时，节点M-J1和M-J2 内部裂缝持续发育，节点区呈现为“X”型交叉裂缝；当θ1=1/86 时，一层各柱根部区域对应裂缝持续延伸，水平裂缝贯通整个柱身，伴随侧向位移不断增加，裂缝数量没有明显增多，但裂缝变长、变宽；当θ2=1/50 时，中部十字节点M-J1 与下部柱C-MI1 顶部水平结合面处出现混凝土压碎现象，之后，依次在节点M-J2 下部柱CMI2顶部及一、二层梁的两端部区域开始出现混凝土剥落现象；当θ1=1/38时，节点M-J1内部混凝土已呈较为严重的剥落，内侧箍筋外露；一、二层梁端部混凝土压碎现象继续发展，一层柱脚区域混凝土亦开始被压碎；当θ1=1/27时，节点M-J1破坏至呈通透状态，清晰可见节点区内部的纵筋外露、箍筋屈服；一层、二层梁端部塑性铰形成，一层T型柱根部混凝土压碎现象内侧重于外侧，中间I型柱破坏相对较轻，至终止加载时其柱脚区两侧混凝土方被压碎，试验结束。

2.2 失效破坏状态

图6所示为试验模型对应塑性铰出铰顺序与位置，整体破坏以梁铰破坏机制为主，符合“强柱弱梁”抗震设计理念，呈延性破坏。图7所示为各节点区的失效破坏状态与“拉-压综合塑性铰”物理长度[22]。

图6 塑性铰出铰顺序与位置Fig.6 Sequence and position of plastic hinges

从图7可知：中间节点M-J1 和M-J2 为推拉复合受力区，呈“X”型剪切裂缝破坏特征，对应梁端塑性铰平均长度分别为63 mm 和49 mm；一、二层梁体外围端部节点对应梁端弯曲破坏，对应塑性铰长度分别为200 mm 和220 mm，分别包括节点S-J1，N-J1，S-J2和N-J2；一层柱根部区域表现为柱脚混凝土压碎破坏，其中外围T型柱（C-NT和C-ST）压碎比中部I 型柱（C-MI）压碎的早，平均塑性铰长度为154 mm。

图7 节点失效状态与塑性铰长度Fig.7 Failure states of joints and length of plastic hinges

3 试验结果与分析

3.1 滞回曲线

采用双作动器按倒三角形规则对模型进行低周往复试验加载，不仅可以直接得到图8（a）和（b）所示各层对应的滞回曲线，而且可以依据合力矩定理得到两加载点对应的合力大小与作用位置，并依据线性内插法求得合力点处的侧向变形，从而可得到图8（c）所示整体模型的荷载-变形滞回曲线。

从图8（a）可知：一层滞回曲线整体呈“Z”形且存在滑移段，对称性相对较差，同种侧向变形对应的抗侧承载力正向外推显著大于负向内收，负向无明显下降段；与一层不同，图8（b）所示为二层滞回曲线整体呈“弓”形且对称性较好，中间捏拢与M-J2 等节点剪切变形试验现象相符，正负向均存在显著下降段，但同种侧向变形对应的正向抗侧承载力小于负向抗侧承载力，与一层呈互补之势，这也是双作动器同步加载的优势，能使模型在低周往复加载过程中的内力重分布得到体现。从图8（c）可知：整体模型的滞回曲线对称性较好，呈反“S”型，相同侧移对应的正向外推抗侧力大于负向内收抗侧力，以峰值荷载为例，正向较负向大15.2%；伴随侧移增加，刚度退化均匀且缓慢，曲线双向均具有明显下降段，且屈服后同级侧移重复加载刚度和承载力下降不明显；存在轻微滑移现象，与装配式结构梁端与后浇区存在连接界面有关。

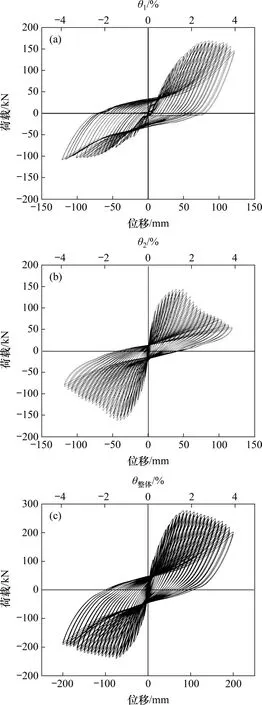
图8 滞回曲线Fig.8 Hysteresis curves

3.2 骨架曲线

图9（a）和（b）所示分别为试验模型各层及整体对应的骨架曲线，其中，P为试件加载端出力，Pcr为试件开裂荷载，Py为试件屈服荷载，Pp为试件峰值荷载，Pu为极限荷载。从图9（a）可知：二层初始刚度比一层的大，二层先达到峰值荷载，对应层间位移角平均值为1/64，之后承载力下降，刚度降低；与此同时，一层承载力随侧移增加而增大，外推至层间位移角为1/36 时达到峰值荷载，内收阶段至试验结束未出现下降段。由图9（b）可知：整体模型对应的骨架曲线对称性较好，可被开裂荷载、峰值荷载分为3个受力阶段，开裂前近似呈直线，结构处于弹性阶段；之后，伴随侧移增加承载力持续增大，但曲线斜率变小，抗侧刚度降低，达到峰值荷载后伴随侧移增加，承载力下降较为缓慢，峰后具有较强变形能力。待塑性铰充分发展、承载力下降至峰值荷载平均值85%以下时，终止试验。

图9 骨架曲线Fig.9 Skeleton curves

3.3 延性与变形

开裂点依据试验现象确定，峰值点依据图9所示骨架曲线确定，失效破坏点取下降至峰值荷载85%对应的位置，屈服点则依据几何作图法[23]确定，可得到表1所示各特征点对应的承载力、变形及层间位移角。从表1可知：一、二层层间开裂位移角θcr分别为1/424 和1/691，一层满足JGJ 149—2017“混凝土异形柱结构技术规程”[5]规定的异形柱框架结构弹性层间位移角限值1/550，二层则小于规范限值，表明二层过早开裂。究其原因是装配式异形柱框架结构在构件拼接处过早开裂及一榀平面框架试验时未考虑楼板、内外墙板对侧向刚度的贡献作用。就极限位移角θu而言，一、二层对应实测值分别为1/25 和1/48，均大于JGJ 149—2017[5]中限值1/50，验证了该二层二跨装配式异形柱框架结构满足“大震不倒”抗震设防要求。

结构的延性通过延性系数μ即极限变形Δu与屈服变形Δy之比表征。由表1和图9（b）可知：试验模型一层、二层及整体结构对应的延性系数分别为2.23，4.57 和4.83，除一层外，其余楼层延性系数均较大，满足延性框架要求；一层延性系数虽较小，但极限变形能力显著比二层的强，至终止试验时内收方向仍未进入峰后下降段，延性系数小，这是屈服变形过大所致。总体而言，该模型各层及整体均具有较强的承载变形能力。

表1 特征值提取Table 1 Extraction of characteristic values

3.4 承载力退化

依据JGJ/T 101—2015“建筑抗震试验规程”[21]提供的方法通过式（2）计算承载力退化系数λi，其值越大，说明结构抗震承载稳定性越好。

式中：λi为第i次循环对应的承载力退化系数；Fji和Fji-1分别为第j次加载时，第i次和第i-1次循环峰值点对应的荷载。

图10所示为试件各层及整体在各加载步对应的承载力退化系数。从图10可知：当一层正向外推加载时，伴随侧移增加，承载力退化系数整体呈减小趋势，负向未见明显退化，与图8（a）所示滞回曲线特征相吻合；对于二层及整体模型对应的承载力退化系数，正负向对称性较好且退化不显著，最小值为0.937，该二层二跨装配式异形柱框架结构具有较强的承载稳定性。

图10 承载力退化系数Fig.10 Degradation coefficients of bearing capacity

3.5 刚度退化

采用同一级幅值加载下的环比刚度表示试件刚度退化规律，计算公式为

式中：Ki为试件第j级幅值加载下的环比刚度；Fji为试件第j级加载时，第i次循环峰值点的荷载；δj为试件第j级加载下对应的位移幅值；n为同一级位移值加载的循环次数，力和位移加载阶段n分别等于1和3。

图11所示为试件各层及整体结构对应的退化曲线。从图11可知：随着加载幅值增加，试件不断损伤，刚度逐渐下降，以试件开裂为界呈先快后慢退化规律；同级加载先外推后内收，故正向刚度均大于负向刚度；至加载后期，试件各层及整体刚度退化缓慢且趋于稳定，一层有效剩余刚度比二层的大，该装配式框架延性较好。

图11 刚度退化曲线Fig.11 Curves of stiffness degradation

3.6 耗能能力

耗能能力是评价结构抗震性能的重要指标之一，依据各循环加载阶段荷载-位移滞回曲线所包围的面积，通过能量耗散系数E和等效黏滞阻尼系数ξeq

[21]定量评价试验模型各层及整体结构的耗能，如图12所示，耗能越大，说明抗震耗能性能越好。从图12可知：E和ξeq变化趋势相同，均伴随侧移增加而增加；以屈服为界呈两阶段特征，屈服前E和ξeq在低位微幅波动，之后大致呈线性增大；极限荷载以后，试件一层、二层和整体结构对应的ξeq分别为0.146，0.120 和0.137，均满足普通混凝土框架结构黏滞阻尼系数大于0.100的要求，表现出结构具有较强的抗震耗能能力。

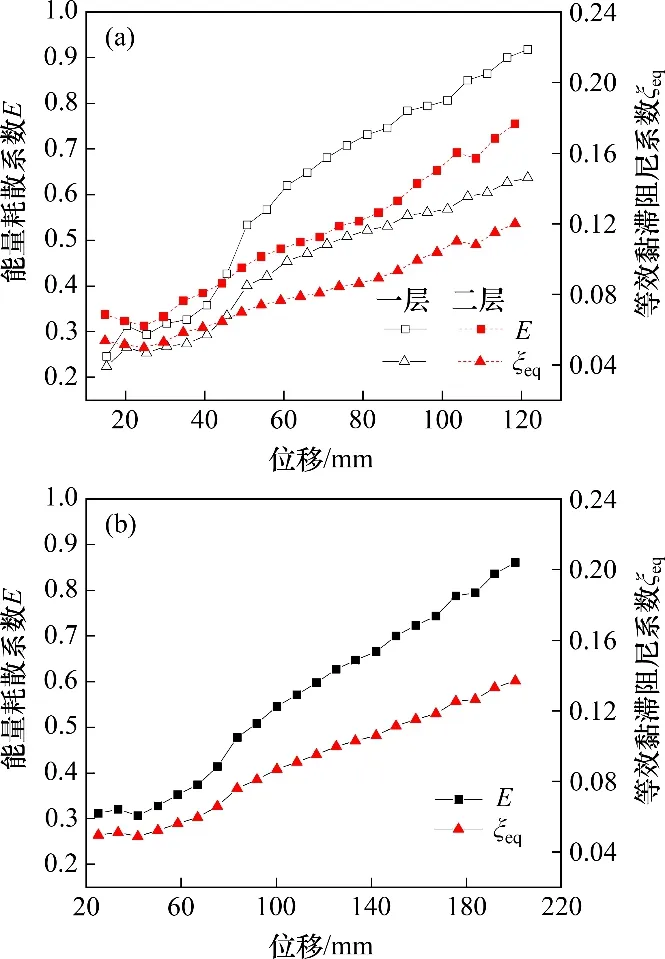
图12 E和ξeq变化趋势Fig.12 Variance tendency of E and ξeq

3.7 浆锚连接区受力分析

由图1可知，试验模型竖向构件采用浆锚连接，这里选取代表性测点开展受力分析。图13（a）所示为T型柱浆锚连接区预制柱内部纵筋与搭接波纹管内部纵筋在同一高度处（中部）的荷载-应变关系曲线。从图13（a）可看出二者在加载全过程受力协调、变形一致。图13（b）和（c）所示分别为一、二层I型预制柱内与搭接波纹管内的纵筋在同一高度处（上部注/出浆口）的荷载-应变关系曲线，其中注浆饱满的图13（c）中二者纵筋应变近似相等、变化趋势相同，而由图13（b）中可知因注浆封堵时浆料回流，顶部注浆口高度处灌浆不密实对应的波纹管内部纵筋应变近似为0。综上可知，浆锚连接区在灌浆质量得到保证的情况下，预制柱内纵筋与搭接波纹管内纵筋对应的受力一致，可全程有效传递荷载；同时，要注意封堵注浆口时浆液短时回流所导致的有效搭接长度缩短问题，宜通过及时补浆等手段保证浆锚搭接区的有效长度。

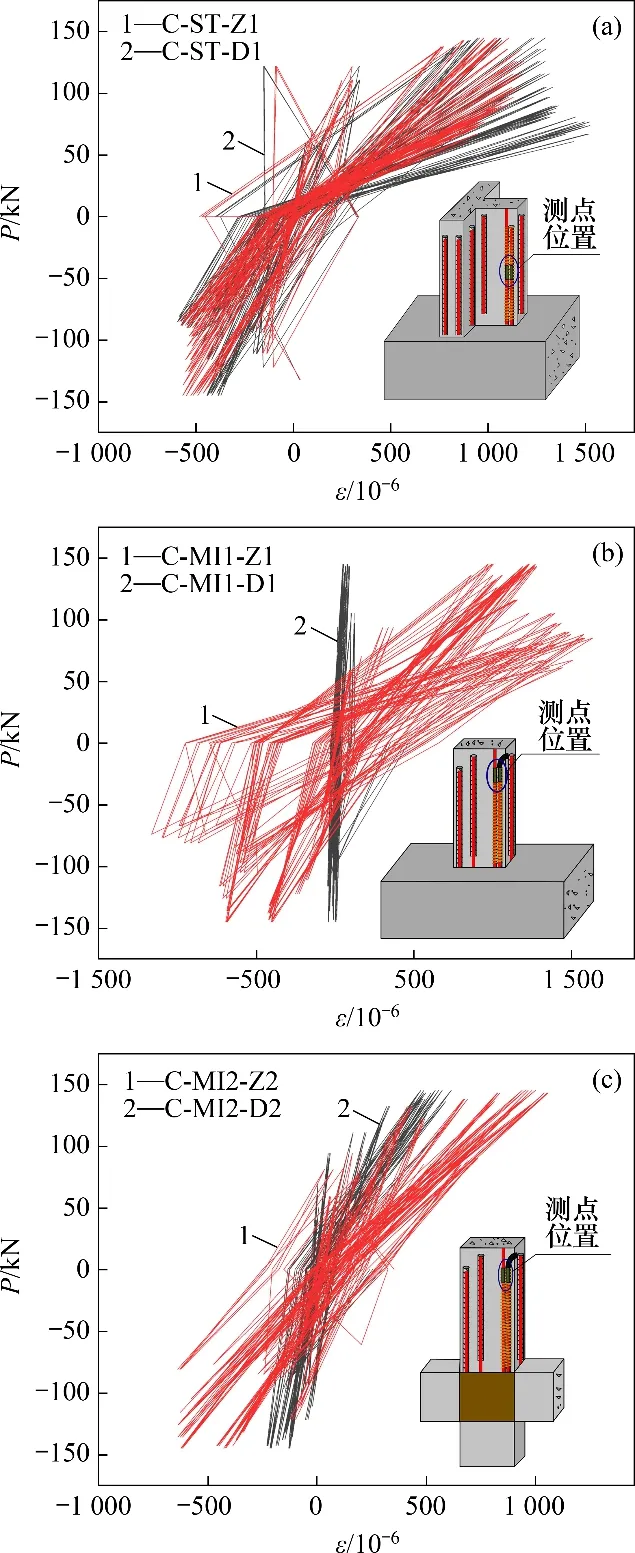
图13 浆锚连接区受力分析（代表测点）Fig.13 Force analysis of slurry anchor connection area（representative of measurement points）

4 基于等效代换的静力弹塑性分析

4.1 异形柱等效代换

由于异形柱框架结构配筋较为复杂，在进行静力弹塑性分析时，截面配筋等信息难以直接输入至当前普遍应用的设计分析软件中。本文基于截面和双向弯曲惯性矩等效原则，将混凝土异形柱原位等效代换为矩形柱[24]，并利用SAP2000程序提供的截面特性修正功能进一步修正等效后矩形截面的横截（轴向）面积、2 个方向的抗剪面积以及扭转常数等，进行混凝土异形柱框架结构的等效代换与静力弹塑性分析。

4.1.1 等效代换公式

假设任意截面异形柱的截面积A是由m个有限的规则单元面积Ai组成，X和Y两坐标轴正交点位于异形柱截面的形心处。设Ix和Iy分别为异形柱绕X和Y轴的弯曲惯性矩，bcx和bcy分别为规则矩形单元在X和Y轴上的截面边长，对应的弯曲惯性矩分别为Ix,i和Iy,i，且形心与X和Y轴的间距分别为dx,i和dy,i。

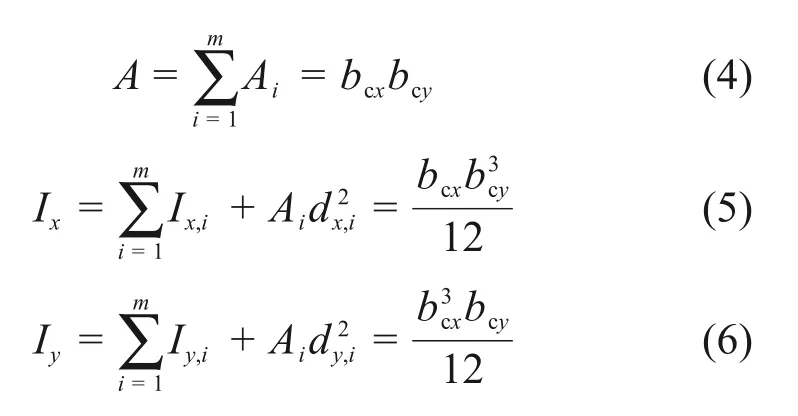
联立式（4）～（6），可求解出任意截面异形柱的等效代换矩形截面边长的解析计算表达式，即

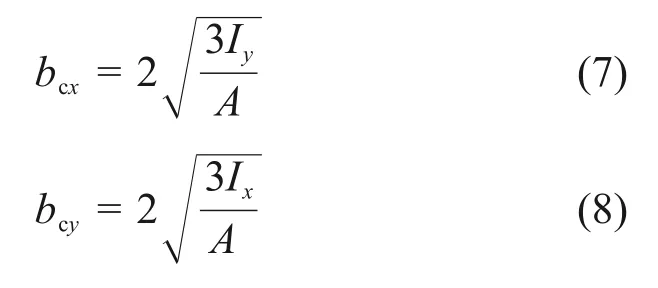
将本文试验模型T型截面异形柱的截面参数代入式（7）和式（8），可分别求得代换矩形截面的边长分别为：bcx=503 mm，bcy=472 mm。为保证等效矩形截面柱对应的拉压区配筋率相等，可根据异形柱截面各受拉区的实配纵筋代换矩形截面相应部位的计算配筋。

4.1.2 截面特性修正系数

为获得高质量的等效代换模型，采用截面特性修正系数（异形柱截面特性与修正后的矩形柱截面特性之比）进行修正，修正系数根据SAP2000 分析原理手册计算。由上述等效代换原则可知，围绕X和Y轴的惯性矩修正系数为1；异形柱与矩形柱的质量、自身重力不变，因此，质量与自身重力修正系数亦为1；横截（轴向）面积和扭转常数修正系数分别为0.758和0.315；加载与垂直于加载方向对应抗剪面积修正系数均为0.505。

4.2 分析模型建立

通过将T 型柱等效代换为矩形截面柱，在SAP2000 分析平台建立模型开展静力弹塑性分析。除等效代换外，材料性能、截面配筋等其他建模参数与试验模型相同；在进行推覆分析时，考虑结构自重影响，对柱底节点施加固结约束。塑性铰通过自定义铰属性设置，对于框架梁单元，考虑由弯矩屈服产生的塑性铰，即采用弯矩铰（M铰）；对于框架柱，考虑轴力与双向弯矩相互作用产生的塑性铰即轴力弯矩铰（P-M-M铰）。塑性铰长度依据图7所示试验结果实测确定，并取混凝土受拉开裂区和受压破碎区的平均长度，然后，根据SAP2000 规定的铰属性定义方法在建模时设置。模型确认无误后，通过Pushover 对异形柱框架开展静力弹塑性分析。

4.3 模型验证与分析

本文开展静力弹塑性分析的目的是：基于等效代换思想为等同现浇装配式混凝土异形柱框架结构的静力弹塑性分析提供可靠的简便分析模型；因物理试验为足尺试验，二层新民居试验原型对应的轴压比较小（南、北两侧T型柱及中间I型柱对应轴压比分别为0.14，0.12 和0.31），加之受加载条件限制，在试验时未考虑轴压比影响，故通过验证后的数值模型分析轴压比的影响。

4.3.1 抗力曲线

图14所示为基于模拟得到的模型顶点侧移-基底剪力抗力曲线。从图14可知：因模拟采用的加载制度与试验不同；屈服前，推覆分析所得抗侧刚度明显大于试验值，这与低周往复加载所致损伤累积有关；屈服后，模拟所得抗力曲线呈现平缓的下降段，最终模拟所得极限荷载、破坏荷载与实测结果相比误差分别为33.37 kN 和28.36 kN。考虑柱顶轴压荷载时，极限荷载提高17.49%，极限变形能力下降，抗力曲线整体外包无轴压工况。

图14 模拟所得抗力曲线Fig.14 Simulated resistance curves

4.3.2 层间位移角

基于图14所示抗力曲线，根据弹性阶段结束点对应变形确定开裂位移模拟值为8.13 mm（实测值为7.22 mm），根据结构破坏荷载对应变形确定模型各层极限位移。经分析可知，在与试验工况等同的无轴压工况下，其一、二层极限位移分别为107.79 mm 和111.28 mm，对应层间极限位移角分别为1/28.4 和1/27.0；考虑轴压后，对应模型的开裂位移提前至5.68 mm，各层极限位移角分别降至1/32.7 和1/30.0。综上可知，因未考虑三板体系，加之结构为装配式，故模型与试验试件均存在过早开裂现象；而极限位移角均可满足规范限值，模拟结果与表1所示试验结果整体吻合较好。

4.3.3 塑性铰

图15所示为基于等效代换的静力弹塑性分析所得塑性铰发展情况。由图15（a）可知：在推覆过程中，2种模拟工况的塑性铰均率先产生于一层加载点梁端，呈梁铰失效特征；之后，一层梁铰继续开展，二层梁铰出现，中间十字节点的柱铰与梁铰先后产生，最后底层柱脚纵筋屈服并产生塑性铰，整体呈“梁柱铰混合屈服机制”破坏模式，如图15（b）和（c）所示。因推覆分析无法考虑往复加载所致损伤累积，故在十字节点复合受力区塑性铰开展顺序与图6所示结果有一定差异，但最终失效破坏状态与试验结果吻合较好。

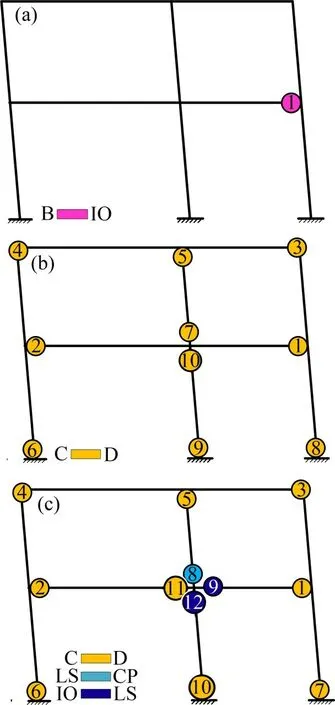
图15 塑性铰发展（静力弹塑性分析）Fig.15 Development of plastic hinges（static elastoplastic analysis）

综上可知，基于等效代换的静力弹塑性分析方法所得到的抗力曲线、层间位移角、塑性铰等与试验结果吻合较好，特别是在抗震设计控制性指标方面吻合度更高，其作为一种简化分析方法用于等同现浇装配式混凝土异形柱框架结构的抗震性能分析是可行的。

5 结论

1）“浆锚连接+节点后浇”方案用于装配式混凝土异形柱框架结构安全可靠；试验模型呈“梁铰”失效破坏特征，梁端裂缝发展范围约为跨度的1/3，符合“强柱弱梁”破坏特征；中间十字节点呈“X”型剪切裂缝，局部损坏较为严重，宜通过增设斜筋、采用高延性混凝土等措施改善。

2）试验模型具有较强的承载变形与耗能能力，满足延性框架要求；具有较强的承载稳定性，刚度退化呈先快后慢且趋稳之势；因构件装配存在拼接缝且未考虑楼板及内外墙板对侧向刚度的贡献，二层层间开裂位移角为1/691，较现浇混凝土异形柱框架结构的规范限值1/550略小；就极限位移角而言，各层均大于规范限值1/50，满足“大震不倒”抗震设防要求。

3）通过将混凝土异形柱原位等效为矩形柱，在SAP2000 平台实现了基于等同现浇设计理念的装配式混凝土异形柱框架结构的静力弹塑性分析，所得模拟结果与试验结果吻合较好，为开展同类结构的推覆分析提供了便捷、可靠手段。考虑轴压影响后，极限荷载略有提高，极限变形能力降低，但极限位移角仍满足规范限值。