螺旋桩竖向抗拔极限承载力理论计算分析

刘志鹏，孔纲强，文磊，郝冬雪，韦芳芳

（1.河海大学岩土力学与堤坝工程教育部重点实验室，江苏南京，210098；2.东北电力大学建筑工程学院，吉林吉林，132012）

螺旋桩的上拔破坏模式主要受其埋深比影响，浅埋时桩周土体会产生延伸至地表的破坏面，而深埋时则表现为锚盘上部土体的局部破坏。针对浅埋工况下的螺旋桩上拔破坏模型，ILAMPARUTHI 等[1]对以往文献进行了全面的总结，认为可归总为延伸至地表的倒圆台型、竖直型和对数螺旋面型破坏面；针对深埋工况下的螺旋桩上拔破坏模型，SELIG等[2]假定上拔破坏面为倒圆台形式，但只会延伸至锚盘以上2D到3D（D为锚盘直径）；SAEEDY[3]假定上拔破坏面为对数螺旋面，破坏面根据土体密实程度向上延伸一定距离，但不会延伸至地表；董天文等[4]假定锚盘附近土体发生塑性滑移，产生梨形破坏面，破坏面由对数螺旋线旋转而成；MOHAJERANI 等[5]对圆柱面剪切法和单叶片叠加法等经典算法进行了系统总结；王钊等[6-10]开展了螺旋桩承载特性相关的系列模型试验和现场试验研究，为螺旋桩承载力的理论计算提供了试验依据。然而，已有研究中螺旋桩承载力计算理论对于破坏形式的假定及计算方法过于简化，比如，国内行业规范[11-12]中沿用倒圆台模型的土重法未将破坏面上的剪应力考虑在内，基于倒圆台法、圆柱面剪切法和单叶片叠加法所得理论计算结果与实测值之间存在较大的误差[4]。

本文作者从浅埋和深埋2种工况出发，在浅埋工况下，通过对待定参数N进行求导对破坏面形式进行最优化处理；在深埋工况下，根据实际破坏面形式提出相对更接近实际破坏形式的破坏面假定及相应的抗拔承载力计算方法。同时，开展砂土地基中螺旋桩上拔承载特性模型试验，为本文理论模型计算提供试验数据支撑。通过与本文模型试验、已有文献试验结果及已有文献中理论计算方法之间的对比分析，验证本文所建立的理论计算模型的准确性与可靠性。

1 理论计算模型的建立

1.1 深埋、浅埋类型的判定

采用ECP（earth contact products）[13]建议的临界埋深比作为螺旋桩深埋或浅埋的判定依据：当H/D＜6（H为首层叶片埋深）时为浅埋，破坏面延伸至地表；当H/D＞6 时为深埋，破坏面在锚盘以上局部发展。深埋与浅埋螺旋桩在抗拔时仅在首层锚盘以上土体的破坏面形式上有所区别[4]，故本文基于单锚盘螺旋桩对理论计算公式进行推导；对于多锚盘螺旋桩的计算方法，根据锚盘间距与锚盘直径之比确定。即当锚盘间距与锚盘直径的比值大于3时，分别按照单锚盘螺旋桩算出每个锚盘的承载力并进行求和计算；当锚盘间距与锚盘直径的比值小于3 时，锚盘间按圆柱面剪切模型计算。

1.2 浅埋螺旋桩破坏模型及公式推导

1.2.1 破坏面模型

研究表明，竖向上拔达到极限状态时，螺旋桩首叶上部的土体由于拖拽作用会被带出，土体破坏形式表现为剪切破坏[14]。假设在极限状态下，螺旋桩锚盘上部产生复合滑裂面，滑裂面上半部为一曲面，该曲面在靠近地表一端与地表夹角为45°-φ/2（φ为内摩擦角），另一端与水平面夹角为90°，曲面总高H1。滑裂面下半部为一圆柱面，圆柱面直径为D。浅埋工况下螺旋桩上拔破坏面形式示意图如图1所示。

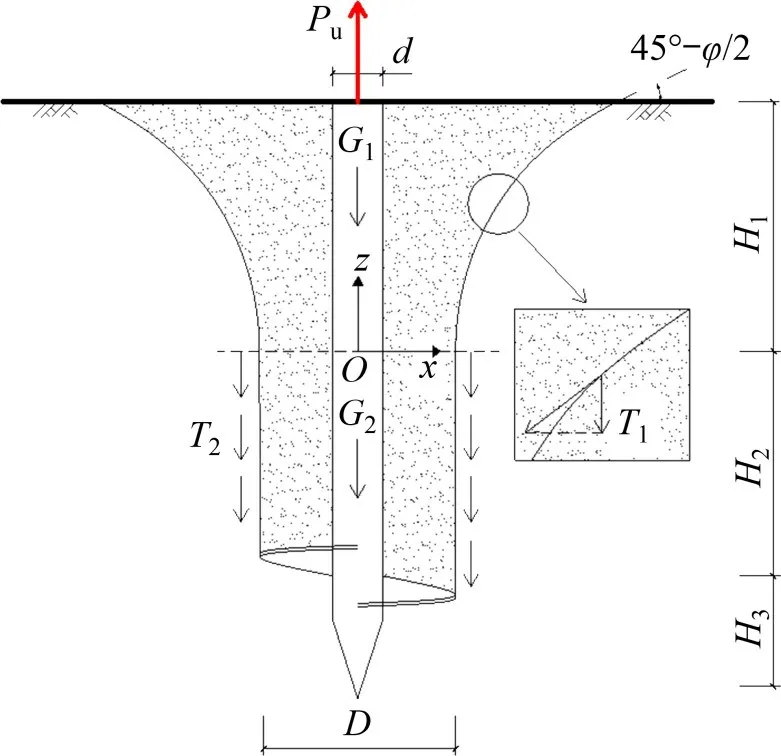
图1 浅埋螺旋桩上拔破坏面模式Fig.1 Failure mode of shallow-buried helical pile under uplift load

1.2.2 控制方程和公式推导

在深度z处，以厚度为dz的单元体作为受力微元，不考虑桩身自重，对各个单元进行受力分析，继而沿深度方向进行积分，便可求出浅埋螺旋桩极限抗拔极限承载力Pu：

式中：T1为对数曲面上的切向力的竖向分力；T2为圆柱面段竖向切向力；G1为对数曲面内土体自重；G2为圆柱面内土体自重。

当0＜z＜H1时，破坏曲面控制方程参照文献[15]给出：

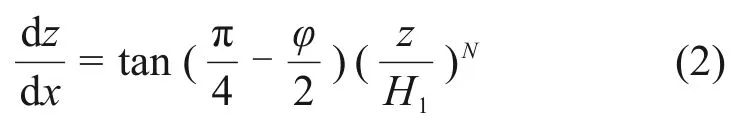
式中：φ为土体内摩擦角；N为待定参数；H1为曲面高度，根据规范DL/T 5219—2014[12]，取H1=2.5D。

对式（2）进行积分可得

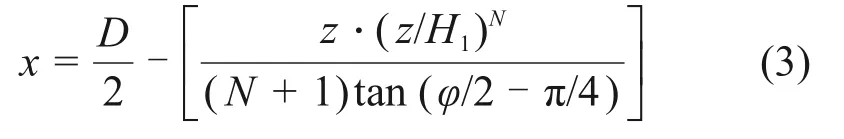
在坐标轴z处，记破坏面的切平面与竖向的夹角为α，则该切平面上的切应力的竖向分量为：

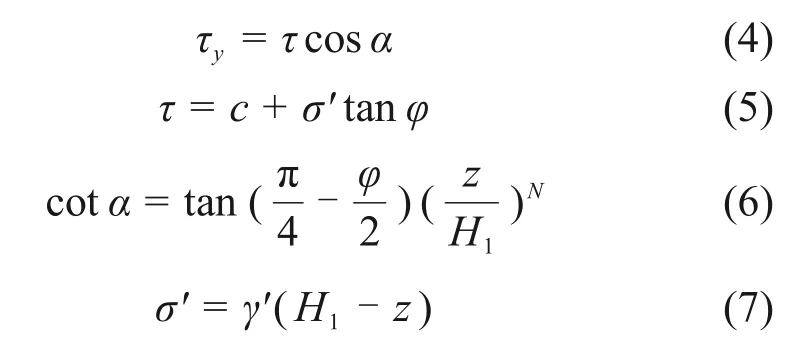
式中：c为土体的黏聚力；σ′为土体的有效应力。

沿深度方向对土体重力和剪应力积分可得：

将式（8）～（11）计算结果代入式（1），可求得浅埋螺旋桩抗拔极限承载力。基于最大值最小值原理，在任意桩型与地层情况下，始终存在一个最危险的破坏滑动面，基于该滑动面求出的极限抗拔承载力最小。因此，对公式中的参数N进行求导，编程求解，可以获得极值情况下的未知参数，从而可以确定螺旋桩的抗拔极限承载力。

1.3 深埋螺旋桩破坏模型及公式推导

1.3.1 破坏面模型

相关研究[16]表明，螺旋桩和平板锚在上拔承载特性上没有明显区别，故此处将螺旋桩简化为平板锚进行公式推导。针对深埋螺旋桩，部分学者根据试验观测结果提出了简化的破坏模型如对数螺旋面形和倒圆台形[2-3]。然而，这些破坏面形式及相应的抗拔极限承载力计算结果与实测值尚存在较大的差异[4]。文献[1]中的试验观测结果显示，上拔荷载下深埋螺旋桩的破坏面呈气球状。基于此，本文假定简化后的破坏面为一椭圆绕轴线旋转而得的闭合曲面（图2），曲面经过锚盘边缘各点且长轴与短轴端点连线与水平方向所夹锐角α为45°-φ/2，破坏面总宽度为λD，λ为待定参数（与埋深比相关）。抗拔极限承载力由破坏面内土体自重、破坏面上切向力的竖向分力、破坏面上方土体自重应力之和以及破坏面上方的桩-土间摩擦力4 个部分组成。

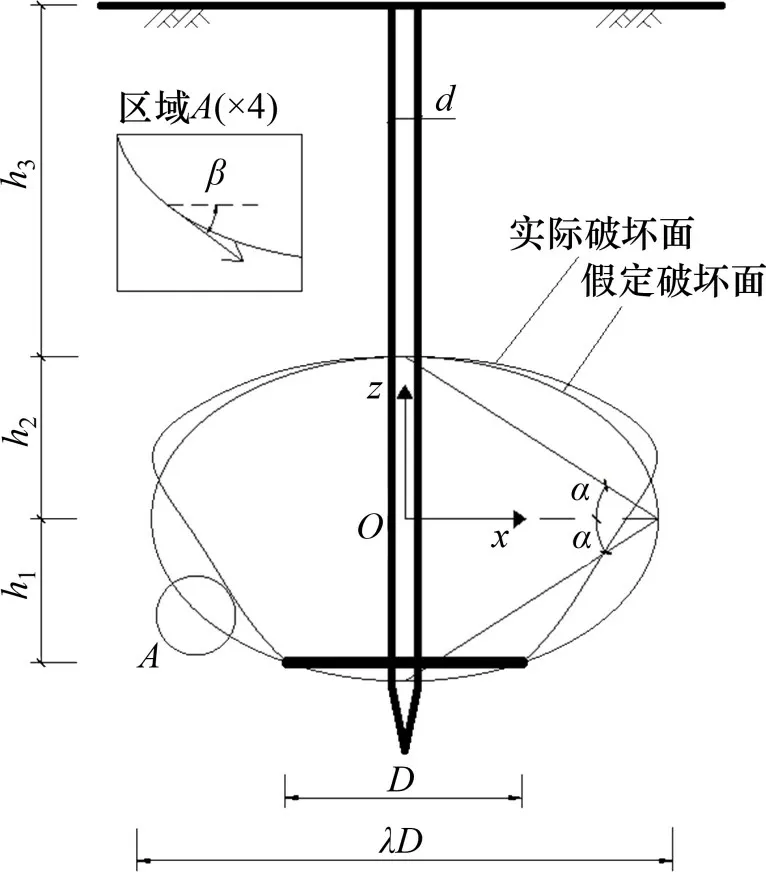
图2 深埋螺旋桩单桩上拔破坏模式Fig.2 Failure mode of deep-buried helical pile under uplift load

1.3.2 控制方程和公式推导

深埋螺旋桩抗拔极限承载力为

式中：G为破坏面内土体自重；T1为破坏面上的切向力竖向分力；T2为破坏面以上桩-土间摩擦力；F为破坏面上方土体自重应力之和。

以椭圆长轴为x轴、短轴为z轴，建立坐标系如图2所示，椭圆长轴长度为

式中：λ为待定参数（由埋深比确定），通过算例总结得出，当H/D=6 时，取λ=1.4；当H/D＞8 时，取λ=1.6；当6≤H/D≤8时，λ通过线性插值求得。

破坏模型中假定椭圆长轴与短轴端点连线与水平方向所夹锐角为α，故可求得椭圆短轴长度：

因此，可得图2中椭圆方程：

取x=D/2，可得锚盘所在处z1：

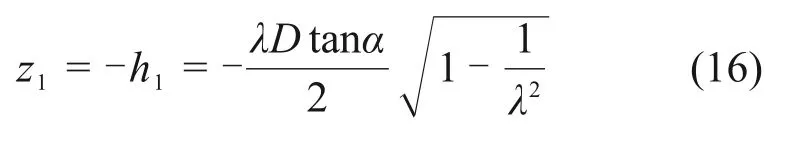
破坏面内土体自重通过积分求解，将破坏面沿深度方向分解为若干单元体，每一单元体可视为厚度dz，直径Di的圆盘，对单元体自重进行求解并沿深度方向积分即可得破坏面内土体总自重。

纵坐标zi处单元体直径为

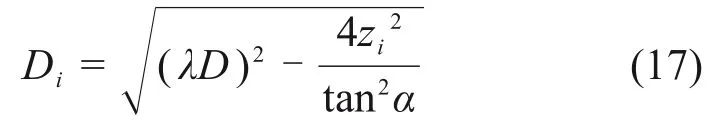
故破坏面内土体自重G为

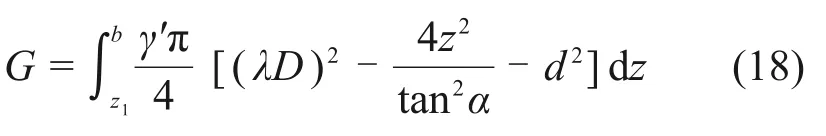
式中：γ’为土体有效重度。

坐标z处对应土体深度为h2+h3-z，无地下水情况下其有效重度σ′为

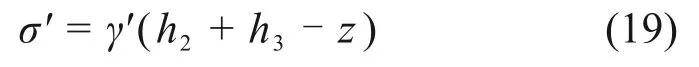
该处土体抗剪强度τ为

由式（15）可进一步求得坐标z处破坏面与水平面所夹锐角β满足如下条件：

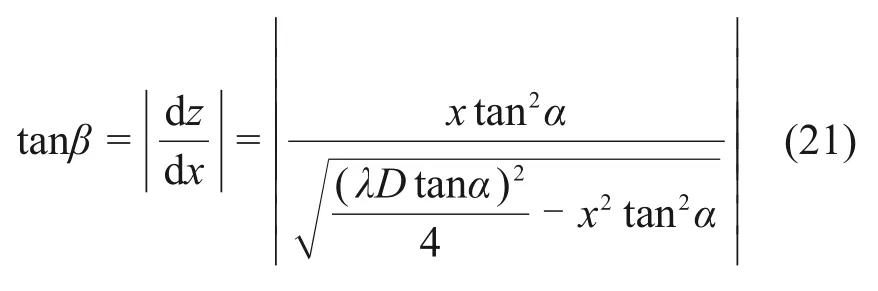
因此，可得破坏面上切应力的竖向分力为

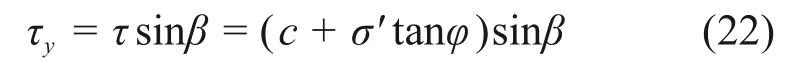
沿深度方向积分可求得破坏面上切向力竖向分力为

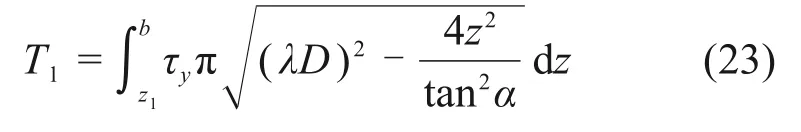
破坏面以上桩土间摩擦力为

式中：K0为静止侧压力系数，取K0=1-sinφ。

椭圆绕z轴旋转而得的空间曲面方程为

故

通过曲面积分计算可得破坏面上方土体自重应力之和：

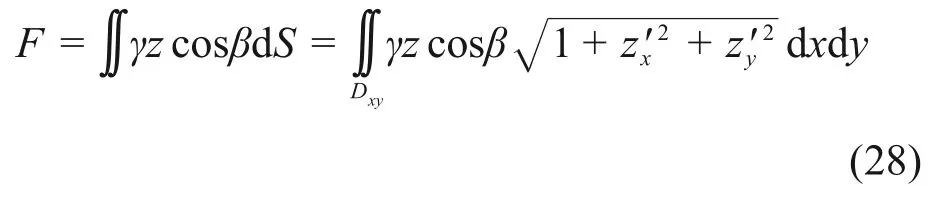
将式（18），（23），（24）和（28）所求结果代入式（12），可求得深埋螺旋桩单桩抗拔极限承载力。

2 螺旋桩竖向上拔模型试验

2.1 模型试验概况

2.1.1 试验模型槽

模型试验系统，包括模型槽、加载系统、数据采集系统等（图3）。试验模型槽长×宽×高为2.0 m×2.0 m×2.5 m。

图3 模型试验系统Fig.3 Model test system

2.1.2 试验土样

试验土样选用砂土，采用人工分层碾实填筑方法进行填筑土料；试验土样的基本物理、力学性质见表1，颗分试验结果见图4。所用砂土的土粒不均匀系数Cu为1.25，曲率系数Cc为0.97，为级配不良砂。

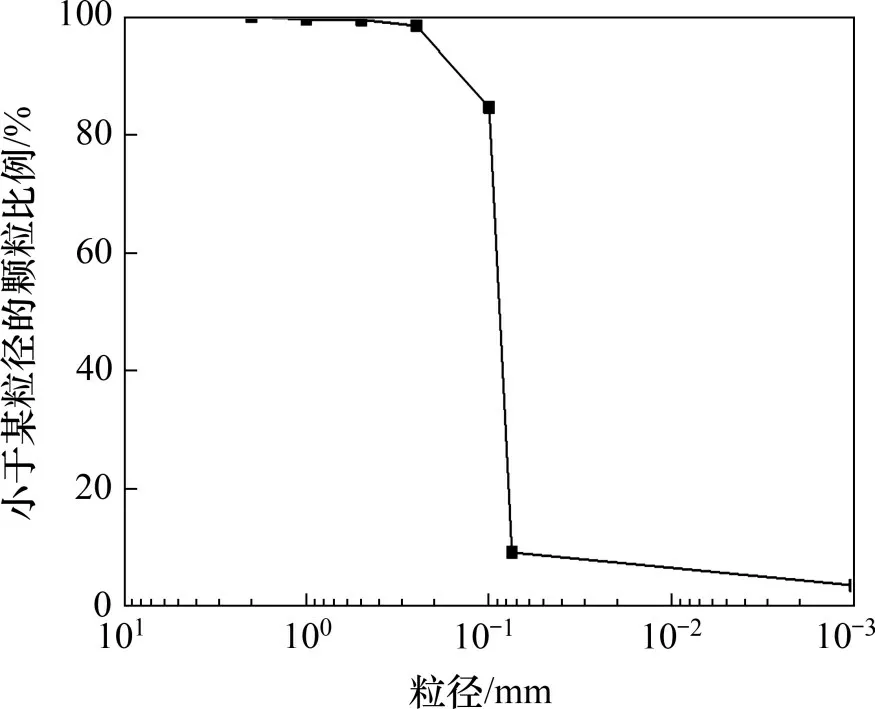
图4 砂土颗粒分析试验曲线Fig.4 Curve of sand particle analysis

表1 试验土样基本物理力学性质指标Table 1 Physical and mechanical properties of soil in model test

2.2 螺旋桩尺寸及试验布置

试验采用国内太阳能光伏电板下常用的螺旋桩在模型槽中开展足尺试验，螺旋桩型式如图5所示，规格尺寸如表2所示。试验布置横截面和纵截面示意图分别见6（a）和6（b）。土压力盒布置于每个锚盘上方，土压力盒与锚盘间有厚度为5 mm的砂土垫层。试验采用维持荷载法分级加载，试验各级加荷量均为试验设计荷载的10%，各级荷载沉降稳定标准以及终止加载条件都参照GB 50007—2011“建筑地基基础设计规范”[17]中关于静载荷试验的内容确定。每级加载结束后，在维持荷载不变以及桩体沉降稳定的前提下，记录桩顶位移以及土压力盒读数，接着加载下一级。

表2 螺旋桩尺寸Table 2 Size of single helical piles

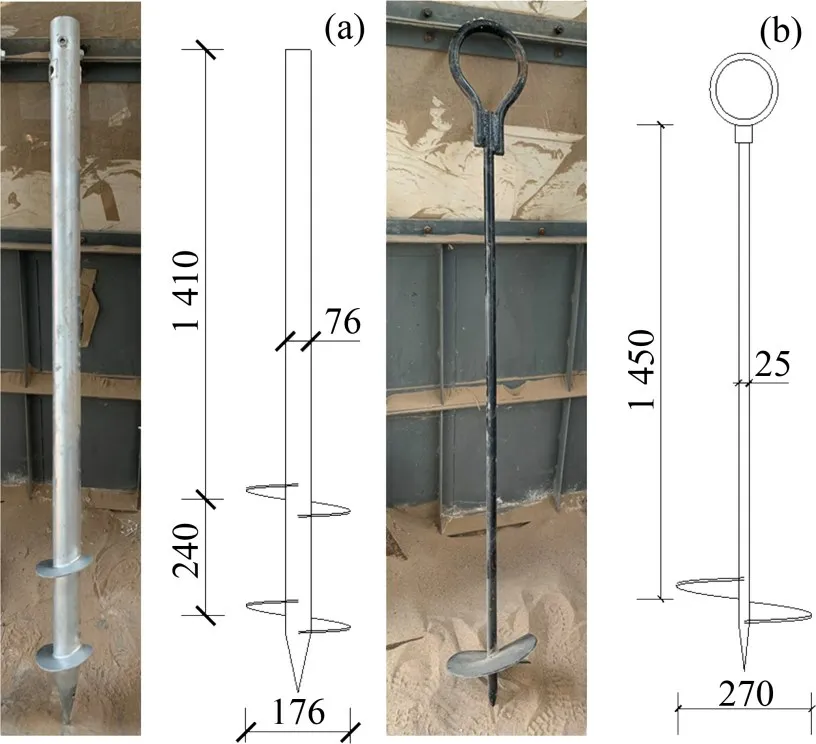
图5 螺旋桩型式Fig.5 Form of single helical piles

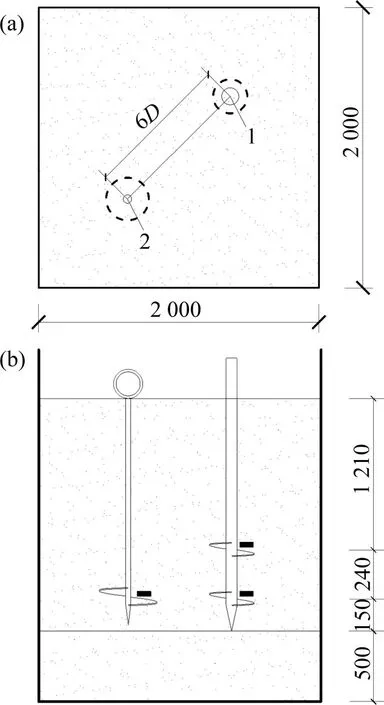
图6 螺旋桩布置示意图Fig.6 Arrangement of helical piles

2.3 模型试验结果与分析

螺旋桩荷载-位移关系曲线如图7所示。由图7可知：2根螺旋桩在上拔过程中整体均表现为缓变型破坏。根据JGJ 106—2014“建筑桩基检测技术规范”[18]规定，本级荷载作用下位移是上一级荷载作用下位移的2倍，且在不稳定的情况下来确定极限承载力，1 号螺旋桩和2 号螺旋桩的抗拔极限承载力分别为3.6 kN和5.2 kN。已有相关研究结果表明[16]，螺旋桩和平板锚在上拔承载特性上没有明显区别，故本文在分析荷载分担过程中，将螺旋锚盘上方土压力盒读数换算而得的土压力减去初始土压力，再乘以该螺旋桩所对应平板锚的锚板实际面积，从而可得到螺旋锚盘承担的荷载。为提高所测土压力的准确性，试验选用振弦式土压力盒，直径约为11.7 mm，紧贴桩身埋设后约土压力盒面积的一半不在叶片正上方，故按本文换算方法所得的叶片荷载分配比理论上小于实际值。

图7 螺旋桩荷载-位移曲线Fig.7 Curves of load versus displacement of helical piles

以1号螺旋桩为例，锚盘上方土压力随荷载变化曲线如图8所示。由图8可知：加载初期，两层锚盘上方土压力较接近；随着荷载增大，首层锚盘上方土压力从22 kPa 逐渐增大至破坏时的54 kPa，荷载分配比则由0 逐渐增大至破坏时的17.7%；第二层锚盘上方土压力随着荷载增大而逐渐减小，土体达到塑性阶段时该位置土压力趋于平稳。这是由于1号螺旋桩锚盘间距与锚盘直径的比值s/D仅为1.36，两层锚盘之间形成圆柱形剪切面破坏。当荷载加至约2.5 kN 时，圆柱形剪切面形成，第二层锚盘上方土压力盒随剪切圆柱体共同向上移动，土压力盒读数基本稳定，不再发生明显变化。

图8 螺旋桩锚盘上方土压力随荷载变化曲线（1号）Fig.8 Curves of soil pressure above plates of helical pile versus uplift load（No.1）

3 理论模型的验证与分析

3.1 本文理论计算结果与试验实测值的对比分析

采用ILAMPARUTHI 等[1,19]模型试验结果，对本文所推导发理论计算公式进行验证，试验土体性质和模型桩尺寸分别如表3和表4所示。将上述已有文献模型试验参数和本文试验结果代入所推导的理论计算公式，求出理论计算结果，并与试验实测值进行对比，所得结果如表5和图9所示。12个算例中，有6个算例为浅埋螺旋桩、6个算例为深埋螺旋桩。由表5和图9可知：6 组浅埋桩算例中有2组计算结果相对误差在10%以内，其余4组相对误差也均小于40%，本文浅埋计算方法计算结果整体偏小，在工程设计中相对偏安全；6组深埋桩算例中，有4组计算结果相对误差在10%以内，其余2组相对误差为15%左右。由此可见，通过本文提出的理论计算公式所得结果与实测结果吻合良好，初步验证了所提出的理论公式的适用性和准确性。

图9 抗拔极限承载力计算值与实测值的比较Fig.9 Comparison between calculated and measured values of ultimate uplift bearing capacity of helical piles

表3 试样土样基本物理力学性质指标Table 3 Physical and mechanical properties of soil in model test

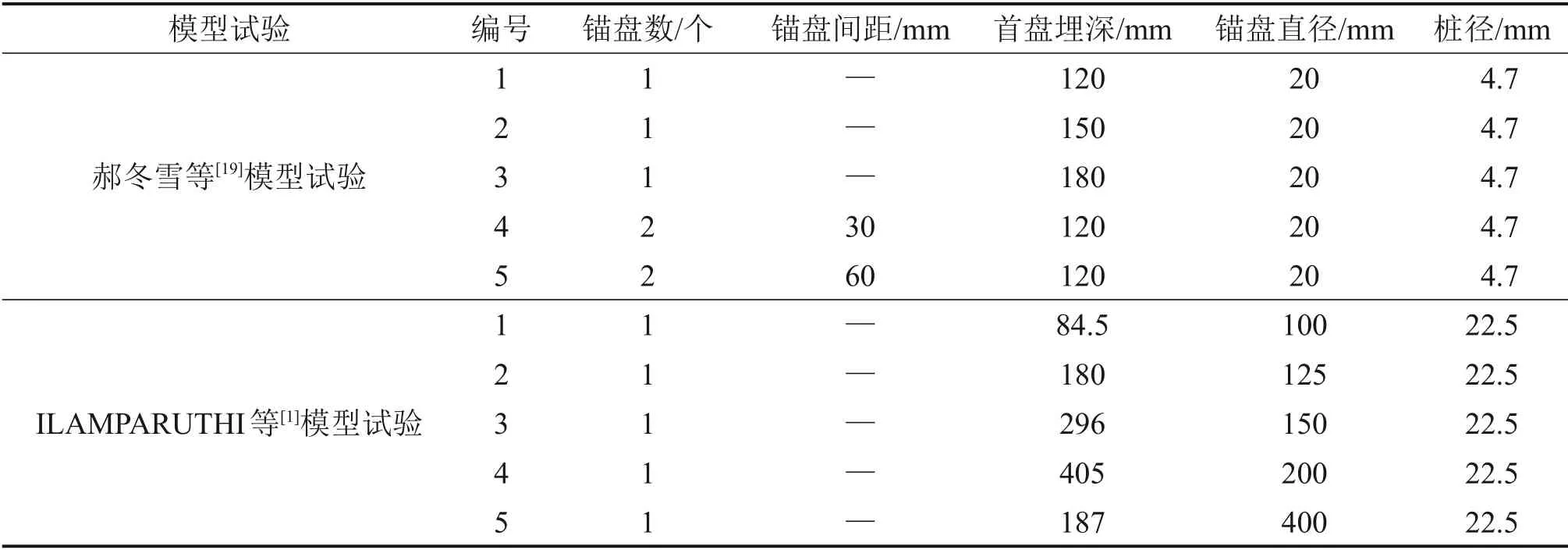
表4 螺旋桩尺寸及抗拔承载力Table 4 Size and uplift bearing capacity of helical piles

表5 模型试验理论计算结果与实测值的对比Table 5 Comparison between theoretical calculation results of model test and measured values

3.2 本文理论计算方法与既有计算方法的对比分析

选用5 种计算理论，包括本文计算方法、Q/GDW 10584—2018 中计算方法[11]、GHALY 等[20]计算方法、CHANCE 单叶片叠加法[5]以及MITSIC和CLEMENCE 圆柱面剪切法[5]，对上述模型试验抗拔承载力理论值进行计算，所得结果如图10所示。由图10可知：由Q/GDW 10584—2018[11]中计算方法所得结果整体偏小，在计算本文算例和ILAMPARUTHI模型[1]试验算例时相对误差在20%～50%之间，但在计算郝冬雪等[19]模型试验算例时，规范计算方法计算相对误差均超过了60%，最大相对误差达到92.2%；GHALY 等[20]计算方法最为简便，计算郝冬雪等[19]模型试验算例和ILAMPARUTHI 等[1]模型试验算例时所得结果整体偏大40%左右，在用该方法计算本文模型试验的抗拔承载力理论值时，理论值与实测值比值高达6，这是因为该方法未将螺旋桩的桩径考虑在内，本文模型试验用桩桩径为76 mm，其桩侧摩阻力以及桩径对锚盘作用的削减不可忽视。此外，GHALY等[20]的计算方法未将多锚盘情况考虑在内，这也限制了该计算方法的适用性。圆柱面剪切法计算所得理论值与实际值相差约60%，误差较大；而单叶片叠加法仅在计算郝冬雪等模型[19]试验理论值时相对误差小于20%，计算其他模型试验理论值时，相对误差均极大（理论值与实测值之比均在5.8～40 之间）。采用本文计算方法计算3 种算例时计算结果与理想线均较吻合，相对误差在可接受范围内，体现了相对较好的适用性。

图10 5种理论计算结果对比Fig.10 Comparison between results of five computing methods

4 结论

1）在本文试验条件下，双锚盘螺旋桩（s/D=1.36）锚盘上方土压力在加载初期较为接近；随着荷载的增大，首层锚盘上方土压力从22 kPa 逐渐增大至破坏时的54 kPa，荷载分配比则由0逐渐增大至破坏时的17.7%；第二层锚盘上方土压力随着荷载增大而逐渐减小，当土体达到塑性阶段时，该位置土压力趋于平稳。

2）利用理论公式估算12 根螺旋桩的上拔承载力，通过与实测值进行对比，在一定程度上验证了本文理论计算公式的适用性及准确性。但是，由于试验数据仅限于模型试验且试验结果案例数量有限，因此，对于本文所提出的理论计算方法的适用性需经过现场试验进一步验证。

3）Q/GDW 10584—2018 中土重法计算值整体相对偏小；GHALY等的计算方法计算值则相对偏大。由于未考虑桩径影响，在计算本文模型试验算例时出现较大误差；圆柱面剪切法计算误差均相对较大；单叶片叠加法适用性较差；本文所提出的理论计算方法具有更好的适用性和准确性。