基于监测数据的在役大跨度桥梁竖向挠度可靠性评估
2021-11-25曾国良邓扬马斌刘涛磊
曾国良,邓扬,马斌,刘涛磊
(1.长沙理工大学土木工程学院,湖南长沙,410004;2.湖南联智科技股份有限公司,湖南长沙,410019;3.北京建筑大学土木与交通工程学院,北京,100044)
服役荷载下的结构变形是大跨度桥梁运营过程中需要重点关注的问题之一。大跨度桥梁的竖向挠度变形直接反映了结构刚度的真实状态,过大挠度会对某些构件的服役性能产生不利影响,例如加剧铺装层裂化、导致混凝土桥面板开裂。美国AASHTO桥梁设计规范[1]和我国的桥梁设计规范[2-3]都对挠度提出了要求,如我国公路悬索桥设计规范规定[2],悬索桥加劲梁由车道荷载频值引起的最大竖向挠度不宜大于跨径的1/250。在设计新建桥梁时,通常将设计荷载施加于结构计算模型,得到挠度或者变形,进而与规范的限值进行比较[4-5],然而,对于运营状态下的大跨度桥梁,由于计算模型误差以及荷载随机性,难以通过理论计算获得桥梁结构的真实挠度响应。
随着结构健康监测技术的发展,近年来出现多种先进的挠度/变形监测技术,如李勇等[6]提出了利用倾角仪测试桥梁变形的方法,并应用于1座下承式钢管混凝土拱桥的主梁挠度监测中;LIU 等[7]设计了基于连通管的大跨度桥梁挠度监测系统,采用成桥荷载试验和运营车载试验验证了该监测系统的精度;FENG 等[8]提出了基于机器视觉的桥梁变形监测方法及系统,并基于监测数据建立了结构动力特性与损伤识别方法;熊春宝等[9]联合运用全球定位系统实时动态监测技术(GPS-RTK)和加速度提出了一种桥梁动态变形监测方法,并应用于1座自锚式悬索桥的运营挠度监测。上述技术方法为大跨度桥梁的运营期挠度/变形监测提供了个性化选择,并逐步在实际工程中得到应用。
然而,如何有效地利用挠度监测数据合理评估大跨度桥梁运营期服役性能,是结构健康监测领域必须深入研究的问题之一。目前,已有学者开始运用极值分析和可靠度理论分析桥梁结构的检测/监测数据[10-14],如MESSERVEY等[10]利用区间极值法处理桥梁监测数据,提出了桥梁活载效应极值建模与可靠度评估方法,并将其应用于美国的1座高速公路桥梁;鲁乃唯等[14]利用桥址车载监测数据与有限元数值,模拟计算了某斜拉桥主梁弯矩响应时程曲线,在此基础上基于Rice 公式给出了斜拉桥主梁弯矩效应的极值外推方法。目前国内外学者大多是从安全性即承载能力极限状态的角度开展研究,且较少直接利用挠度监测数据开展在役大跨度桥梁适用性即正常使用极限状态评价。鉴于此,本文作者提出基于竖向挠度监测数据的大跨度桥梁可靠度评估方法,根据极值分析理论和可靠度理论建立可靠度评估方法的理论框架,并以某悬索桥为研究背景,给出不同服役期内加劲梁竖向挠度的可靠度评估结果。
1 可靠度评估方法框架
1.1 车辆荷载挠度识别
对于大跨度桥梁,特别是缆索承重桥梁,恒载效应在竖向挠度中占主导地位,由活荷载引起的挠度幅值相对较小,但影响大跨度桥梁结构运营期性能。
识别车辆荷载引起的挠度步骤主要包括:1)消除挠度原始监测数据中的温度影响分量;2)提取车辆荷载产生的挠度局部极值序列。根据文献[7],大跨度桥梁竖向挠度主要包括3 个分量:环境温度变化产生的挠度、车辆荷载引起的挠度和测试噪声产生的伪挠度。LIU 等[7]研究表明环境温度变化引起的挠度主要是低频的昼夜起伏变化,而车辆荷载引起的挠度则是相对高频的瞬时颤动变化,而测试噪声产生的挠度则显著比前两者的小,基于上述认识,可以采用小波包分解的方法有效消除挠度中的温度分量。
消除环境温度对竖向挠度数据的影响之后,采用局部极值搜寻算法去除挠度中的“无意义”数据。图1所示为车辆荷载竖向挠度识别流程。以图1为例,点3、点4和点5是由同一辆车引起的挠度测试点,显然,点4所测挠度是该段挠度监测数据中的局部极值,点3和点5所测挠度则是在测试过程中产生的“无意义”数据,有可能将其与点4所测挠度同时纳入超越(exceedances)数据序列。采用三点比较算法搜寻提取挠度数据局部极值,该算法的具体思路是:
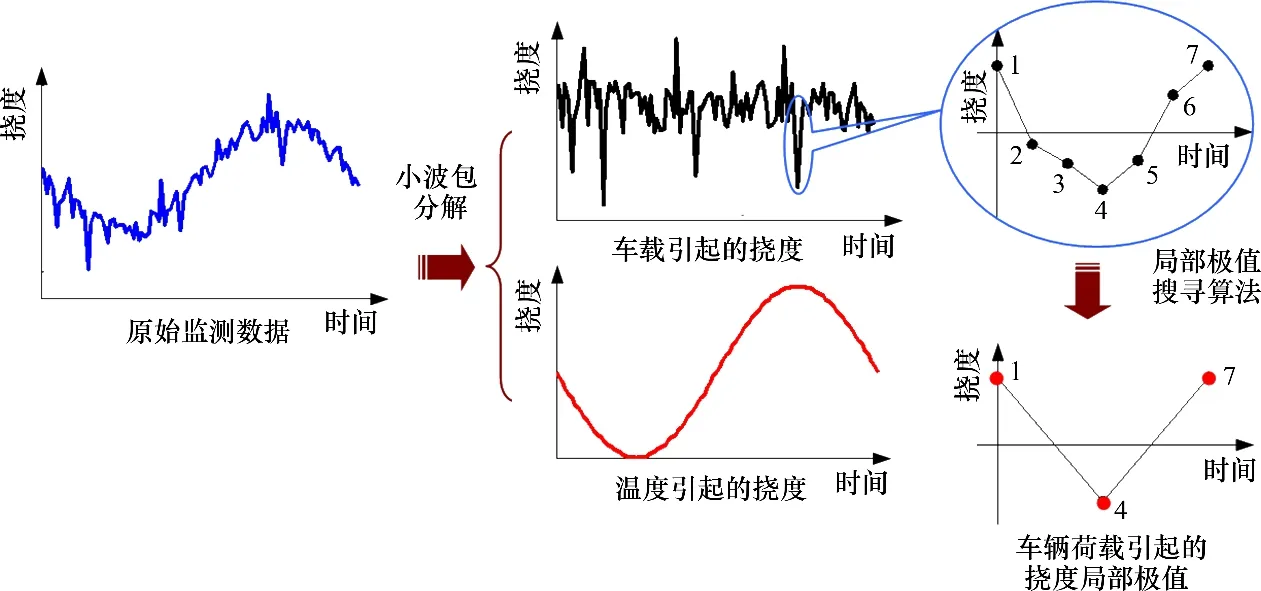
图1 车辆荷载竖向挠度识别流程Fig.1 Flow chart of vehicle-induced deflection identification
1)比较临近的点2、点3和点4的挠度,由于点2、点3和点4的挠度依次降低,因此,删除点3。
2)比较点2、点4 和点5 的挠度,由于点2 挠度大于点4 挠度,且点5 挠度大于点4 挠度,点4为局部极小点,提取点4作为其中1个极值点。
3)持续比较临近三点的挠度,直至提取出所有的局部极大点和极小点为止。
1.2 基于超越阈值法的概率模型
目前已提出多种车辆荷载效应尾部样本的概率分布模型[7,10,12],常用的主要建模方法有区间极值法和超越阈值法(peak over threshold,POT)。区间极值法仅考虑某个时间区间内的荷载效应的最大值和最小值,因此,部分有效信息会丢失。采用POT 方法建立大跨度桥梁竖向挠度尾部样本的GPD (generalized pareto distribution)分布模型,具体建模过程如下:
设X1,X2,…,Xn为一组独立同分布的随机变量,定义阈值为某一特定数值u。当Xi>u时,Xi称之为超越样本。因此,可得到超越样本的分布函数Fu(x):
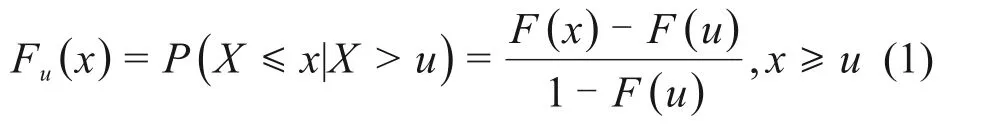
超越样本的分布函数Fu(x)可根据某个确定的母体分布函数F(x)推导得到。当F(x)未知时,GPD分布是超越样本的渐进分布,文献[15-16]指出,当阈值u足够大时,超越样本近似服从GPD分布。GPD分布的概率分布函数Fu(x,u,σ,ξ)为
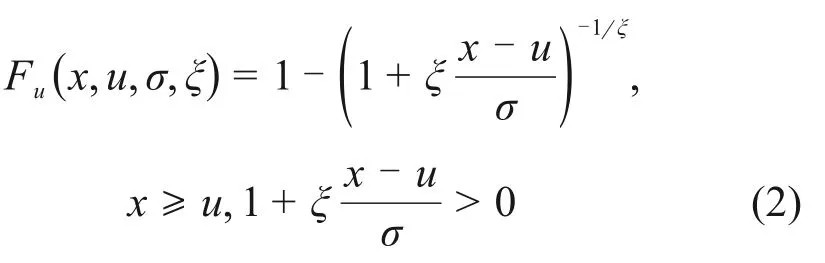
式中:u为阈值;ξ和σ分别为形状参数和尺度参数。
在GPD建模中,选择合适的阈值u至关关键,应综合考虑模型的偏差与方差:太高的阈值会减少超越样本的数量,从而导致较大的方差;反之,超越样本虽然会增多,方差减小,但模型的偏差则会增大[17]。本文提出一种综合作图法和拟合优度检验法的阈值u确定方法,最常用的作图法是剩余寿命图法(mean residual life plot,MRLP)[18],在MRLP中,定义平均超出函数e(u)为
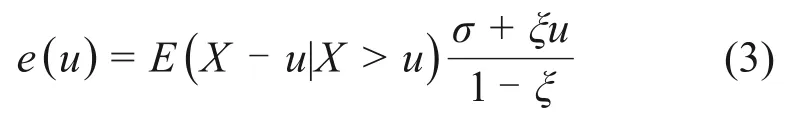
根据式(3),确定阈值u的方法为
1)阈值u为自变量,平均超出函数e(u)为因变量,做出函数的图形;
2)可使函数e(u)曲线近似线性变化的阈值即为合理阈值。
然而,MRLP方法需要主观判断,实施起来有一定困难。CHOULAKIAN等[19]提出采用拟合优度检验的方法来确定合理的阈值,即在给定的显著性水平下,当零假设H0不被拒绝时,此时的阈值可视为合理阈值,本文采用A2Anderson–Darling检验,其统计量为

式中:X1,X2,…,Xn为升序排列的统计样本,X1≤X2≤…≤Xn;F为待检验分布的理论概率分布函数。
在实际计算过程中,除需主观判断外,MRLP方法还可能存在以下问题:通过e(u)函数曲线的线性变化确定最小阈值,该阈值并不能保证此时的GPD 分布模型通过拟合优度检验。而选择合理阈值u的最主要目的是获得超越样本的最优拟合,因此,本文确定阈值的方法是:当平均超出函数e(u)随着阈值u线性变化时,使GPD 分布模型取得最优拟合的阈值即为合理阈值。
1.3 挠度极值模型
滤过泊松过程通常被用作描述车辆荷载的概率模型[20],考虑到车辆荷载引起的桥梁挠度与车辆荷载本身的相似性,亦可采用滤过泊松过程来建立桥梁车载挠度的概率模型。图2所示为滤过泊松过程。车辆荷载效应可视作一系列随机脉冲的组合,图2中每个随机脉冲Si的发生时间和持续时间分别为Ti和τi,通常,车载效应随机脉冲的持续时间要远小于桥梁服役时间。当荷载效应Si(i=1,2,…,k)为一组独立同分布的随机变量时,在时间区间(0,T)内,荷载效应发生次数N(T)的概率为[12]
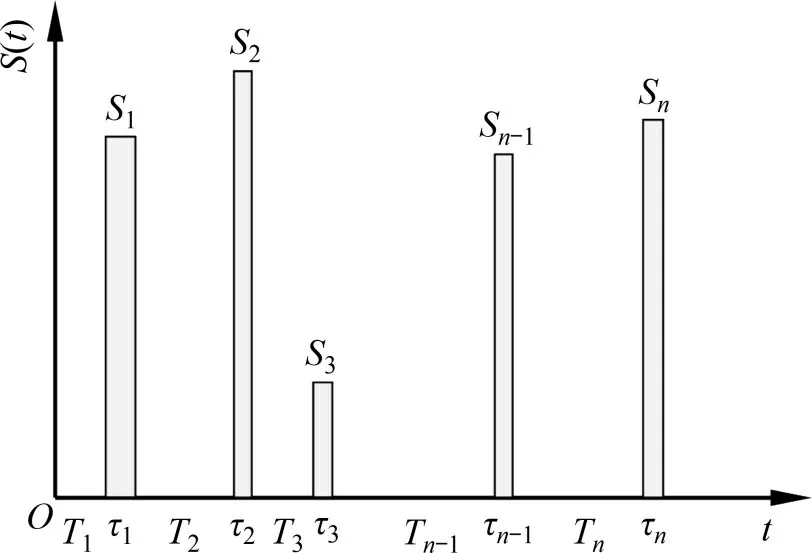
图2 滤过泊松过程Fig.2 Filtered Poisson process

式中:λ为荷载效应的发生率。
因此,可得到车载竖向挠度的极值概率分布FSmax(s)为
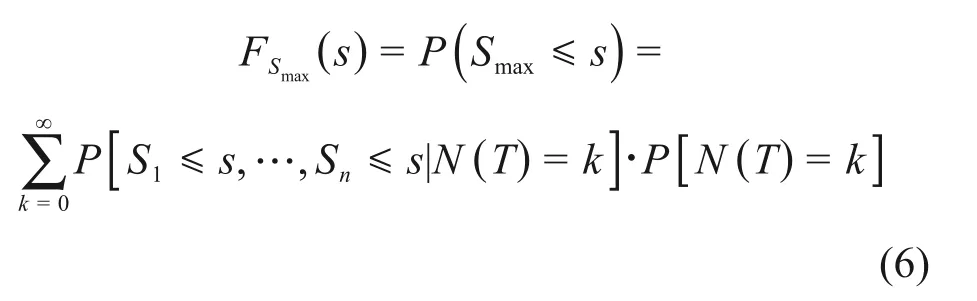
由于Si(i=1,2,…,k)是独立分布的,式(6)可改写为
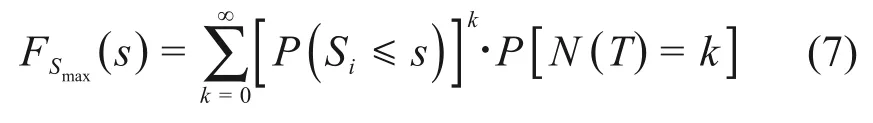
当车载竖向挠度的概率分布函数为F(s),将式(5)代入式(7),可得

从式(8)可知,影响车载竖向挠度极值概率分布的因素主要有荷载效应发生率λ、服役时间T和车载竖向挠度的概率分布F(s)。
前面建立了超越样本的GPD 分布函数,通常极值分布模型FSmax(s)主要受底分布F(s)右侧尾部形状的影响,可采用超越样本的GPD 分布函数得到极值概率分布FSmax(s)。令Fu(s)为概率分布F(s)的超越分布模型,其中u为阈值,则由式(1)可知

车载竖向挠度的超越样本亦可以采用滤过泊松过程来描述,根据式(8),超越样本的概率极值分布Fu,Smax(s)为
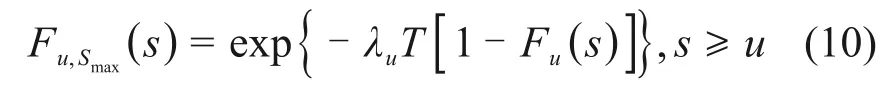
式中:λu为超越样本的发生率。将式(9)代入式(10)可得

在相同的时间区间(0,T)内,超越样本的发生率λu可以近似由荷载效应的发生率λ得到
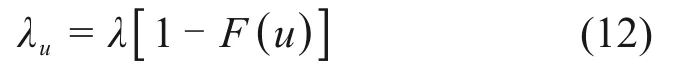
将式(12)代入式(11),可得到超越样本极值分布的表达式为

从式(13)可以看出:超越样本极值分布Fu,Smax(s)与车载竖向挠度的极值分布FSmax(s)具有相同的表达式,可以采用Fu(s)而不是F(s)来得到FSmax(s)。在式(2)中,采用GPD 分布得到超越样本的概率分布,将式(2)中的x换为s,然后将式(2)代入式(10),从而得到车载竖向挠度得极值分布函数FSmax(s):
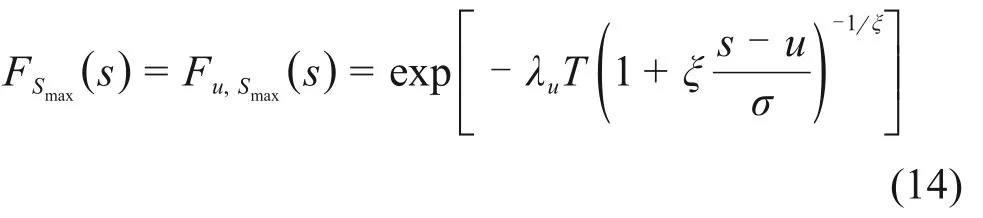
式中:T为桥梁服役期。令
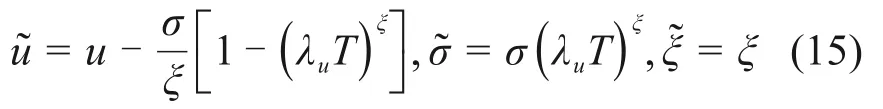
式(14)可以改写为[21]

从式(16)可知:当采用GPD分布为荷载效应超越样本的概率分布函数时,荷载效应的极值分布为广义极值分布GEVD(generalized extreme value distribution)。
1.4 可靠度计算方法
在上述方法的基础上,采用可靠度理论评估大跨度桥梁车辆荷载引起的竖向挠度。针对设置多个监测截面的大跨度桥梁,提出基于多监测截面的体系可靠度评估方法。假定大跨度桥梁主梁有m个截面安装了挠度传感器,则可得到每个传感器安装截面竖向挠度的极限状态方程,进而可以计算每个截面的可靠度指标,
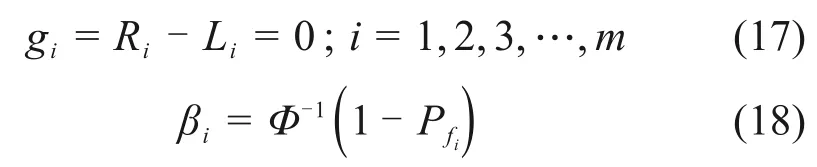
式中:gi为截面i的极限状态方程;βi为可靠度指标;m为桥梁上安装挠度传感器的截面数量;Φ-1(·)为标准正态分布的逆概率分布函数;Ri为挠度限值,反映桥梁结构适用性要求,Ri可以采用桥梁设计规范的允许挠度,或者采用设计荷载作用下的竖向挠度计算值。需要说明的是,在式(17)中,Ri为常量,而Li为随机变量,代表截面i车载竖向挠度的极值。
采用串联模型描述大跨度桥梁车载竖向挠度的多截面失效模式,即一旦某个安装传感器的截面竖向挠度超过了挠度限值,就意味着体系失效。需要说明的是,本文所述体系失效并不意味着结构的安全性失效(如截面抗弯、抗剪失效等),而是从结构适用性的角度描述挠度超限这一失效模式。可将每个安装传感器的主梁截面模拟为串联体系中某个单元,借用结构串联体系的概念描述各监测截面可靠度的关系,从而给出基于监测数据的大跨度桥梁运营期适用性的综合评估结果。采用窄界可靠度方法计算上述准串联体系模型的可靠度[22],体系失效概率的上下界可以定义为

式中:Pf为体系的失效概率;Pfi为第i个模式(传感器安装截面)的失效概率;Pfij为模式i和j的联合失效概率,可以采用数值积分的方法计算得到。将所有失效模式按照失效概率从高到低的顺序排列,Pf1表示体系中失效概率最大值。联合失效概率Pfij可以通过对二元正态分布函数进行数值积分得到[22]:
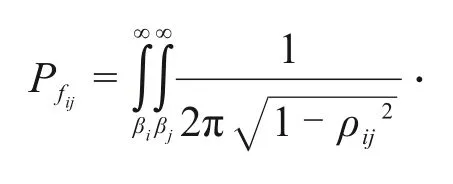
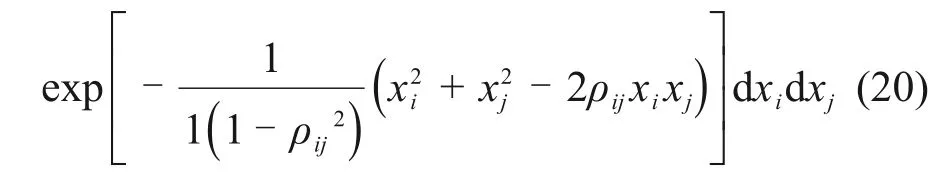
式中:βi和βj分别为模式i和j的可靠度指标;ρij为两者之间的相关系数。
由式(17)可知,ρij仅与随机变量Li和Lj有关。

式(21)中ρLiLj可根据挠度监测数据计算。得到失效概率的上下界后,可得到可靠度指标的上下界为

基于上述推导过程可知,采用本文所提方法可对安装挠度监测系统的大跨度桥梁进行分析。在竖向挠度可靠度计算方法中,将某个截面的竖向挠度超限定义为一种结构适用性的失效模式,在此基础上,借用体系可靠度理论中的串联模型描述大跨度桥梁主梁各截面竖向挠度失效模式之间的关系,从运营期结构适用性的角度提出了竖向挠度可靠性的评估方法。
2 实例分析
2.1 挠度监测数据分析
以某悬索桥为研究背景,该桥主跨跨度为820 m。图3所示为悬索桥挠度测点布置。由图3可见:桥梁安装基于连通管的竖向挠度监测系统,可实时获取运营状态下悬索桥的竖向挠度;主跨等间距布置7个挠度测试截面,每个截面的上下游各安装1个压力传感器,同时在宜宾侧的索塔内安装1个基准压力传感器。目前国内外针对连通管挠度监测技术开展了大量研究[7,23]。以传感器S5(图3中截面3 下游压力传感器)2014-02-14 采集的数据(图4(a))为例,采用Daubechies25 小波函数对原始监测数据进行小波包分解,分解层次为12,图4(b)所示为从挠度原始监测数据中提取出的环境温度分量,图4(c)所示为消除温度影响后的竖向挠度。
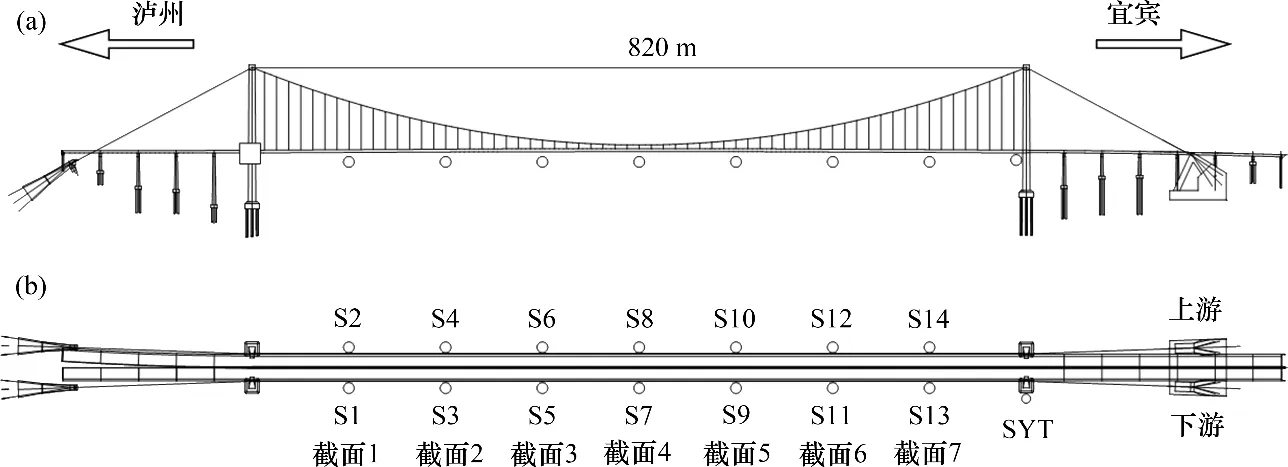
图3 悬索桥挠度测点布置Fig.3 Deflection sensor arrangement of suspension bridge
对每个截面上下游的挠度进行对比分析,选择上下游某个传感器采集的挠度代表该截面的竖向挠度。对2014年2月中25 d 的挠度进行分析,得到类似图4(c)中消除温度影响后的竖向挠度,将每个传感器去除温度影响后采集的挠度定义为Di(i=1,2,…,14)。在此基础上针对每个监测截面,分析上下游监测数据的相对大小关系。以截面3为例,图5所示为上下游挠度监测数据的线性回归方程,图5中回归直线近似通过坐标原点,直线斜率直接反映了每个截面上下游挠度监测数据的关系,直线斜率为0.95,从统计意义上来说,D5比D6大30%,因此,采用下游传感器S5 采集的挠度代表截面3的竖向挠度,其他截面的上下游挠度的对比分析与截面3的类似。分析表明,可分别采用传感器S2,S4,S5,S8,S9,S11和S13采集的挠度代表截面1至截面7的竖向挠度。
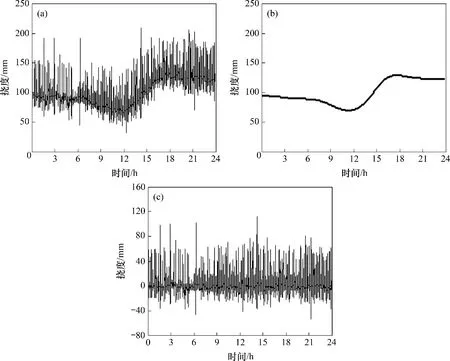
图4 2014-02-14挠度监测数据Fig.4 Deflection data measured on Feb.14,2014

图5 截面3上下游挠度监测数据的线性回归方程Fig.5 Linear regression equation of upstream and downstream deflection of Section 3
式(21)表明可采用各截面挠度极值分布的相关系数ρLiLj代替各截面失效模式的相关系数ρij。然而,由于难以直接得到ρLiLj,故近似采用ρDiDj代替ρLiLj。图6所示为各截面竖向挠度之间的相关系数矩阵。图6中,ρL1L2等于ρD2D4,这是因为采用传感器S2 和S4 采集的挠度来代表截面1 和截面2 的竖向挠度。

图6 各截面竖向挠度之间的相关系数矩阵Fig.6 Correlation matrix of vertical deflection of mounted sections
2.2 极值分布模型
以截面3 的传感器S5 采集的挠度监测数据为例说明阈值u的选择及极值建模过程。首先,采用局部极值搜寻算法从图4(c)所示的消除温度影响的挠度中提取局部极值,进而将局部极值取绝对值,结果如图7所示。在此基础上,采用最大似然法进行GPD分布参数估计[24]。图8所示为截面3的GPD拟合结果随阈值的变化情况,图8(b)中H0表示不拒绝零假设,H1表示拒绝零假设,假设检验的显著性水平设定为0.05,图8(b)中给出了3 个关键点,其中第1 个关键点表示阈值u为58 mm,当阈值大于58 mm 时,不拒绝GPD 分布;第2 个关键点表示阈值u为63 mm,当阈值大于63 mm时,图8(a)中的MEF函数e(u)开始随着阈值线性减小;第3 个关键点表示阈值u为71 mm,此时可得到p的最大值,表示此时拟合效果最佳。
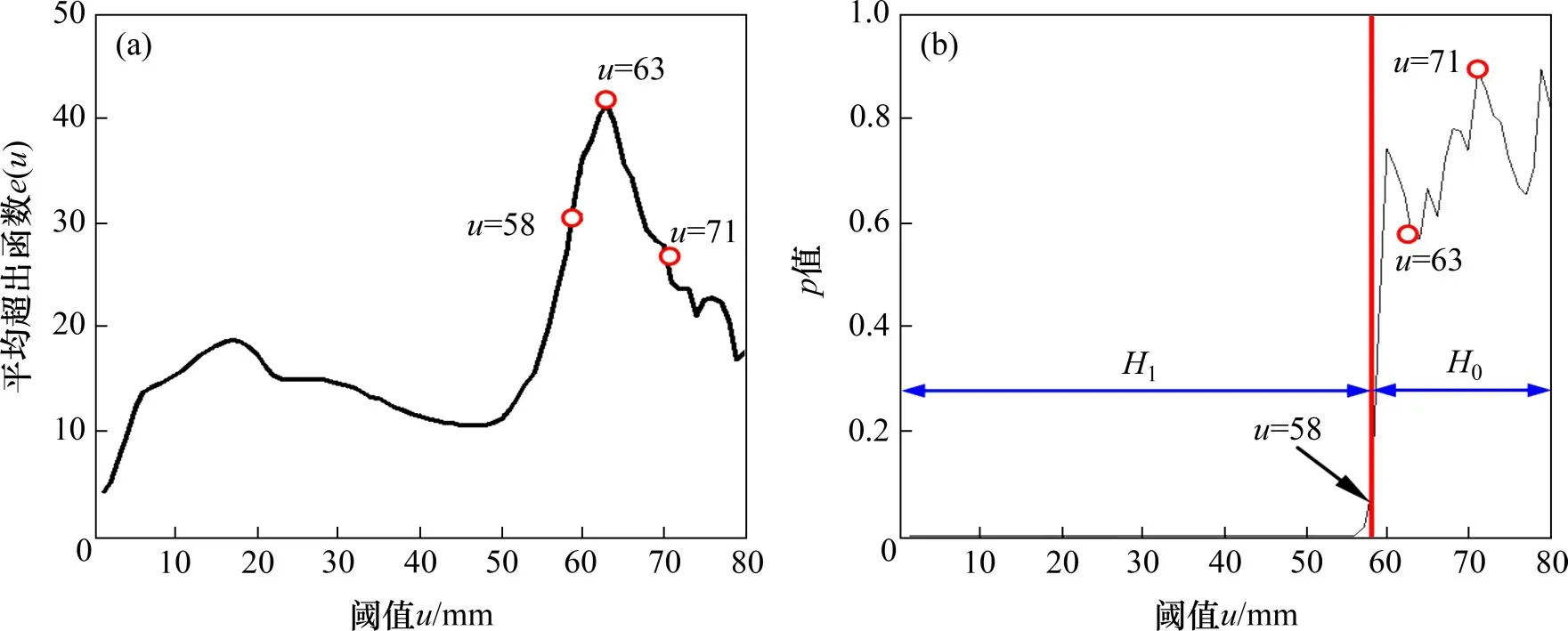
图8 截面3的GPD拟合结果随阈值的变化情况Fig.8 Change of fitting results of GPD of Section 3 with thresholds
图9所示为3种不同阈值的GPD分布Q-Q图,当阈值为58,63 和71 mm 时,分别有1 144,608和241 个超越样本点(见图7)。从图7可以看出:当阈值为58 mm 或63 mm 时,有大量的样本点偏离Q-Q图中的直线,而当阈值为71 mm 时,几乎所有的样本点都分布在Q-Q图的直线附近,表明当阈值为71 mm时,可得到最佳拟合的GPD分布,因此,对于截面3 的挠度,合理阈值设定为71 mm。采用最大似然法估计GPD 分布的形状系数ξ和尺度系数σ,同样以截面3的数据为例,25 d的超越样本点数为241,因此,超越样本的年发生率λu为3 518.6(365×241/25)。在此基础上,依据式(15)计算GEVD极值分布的参数。假定桥梁的服役期T为100 a,则GEVD 分布的参数u˜,σ˜和ξ˜分别为458.2,58.2和0.116。类似地,可以计算其余截面监测数据的概率分布,结果见表1。
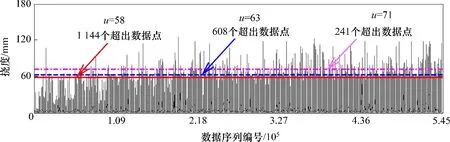
图7 传感器S5(截面3)的挠度局部极值数据Fig.7 Deflection local extremes of sensor S5(Section 3)
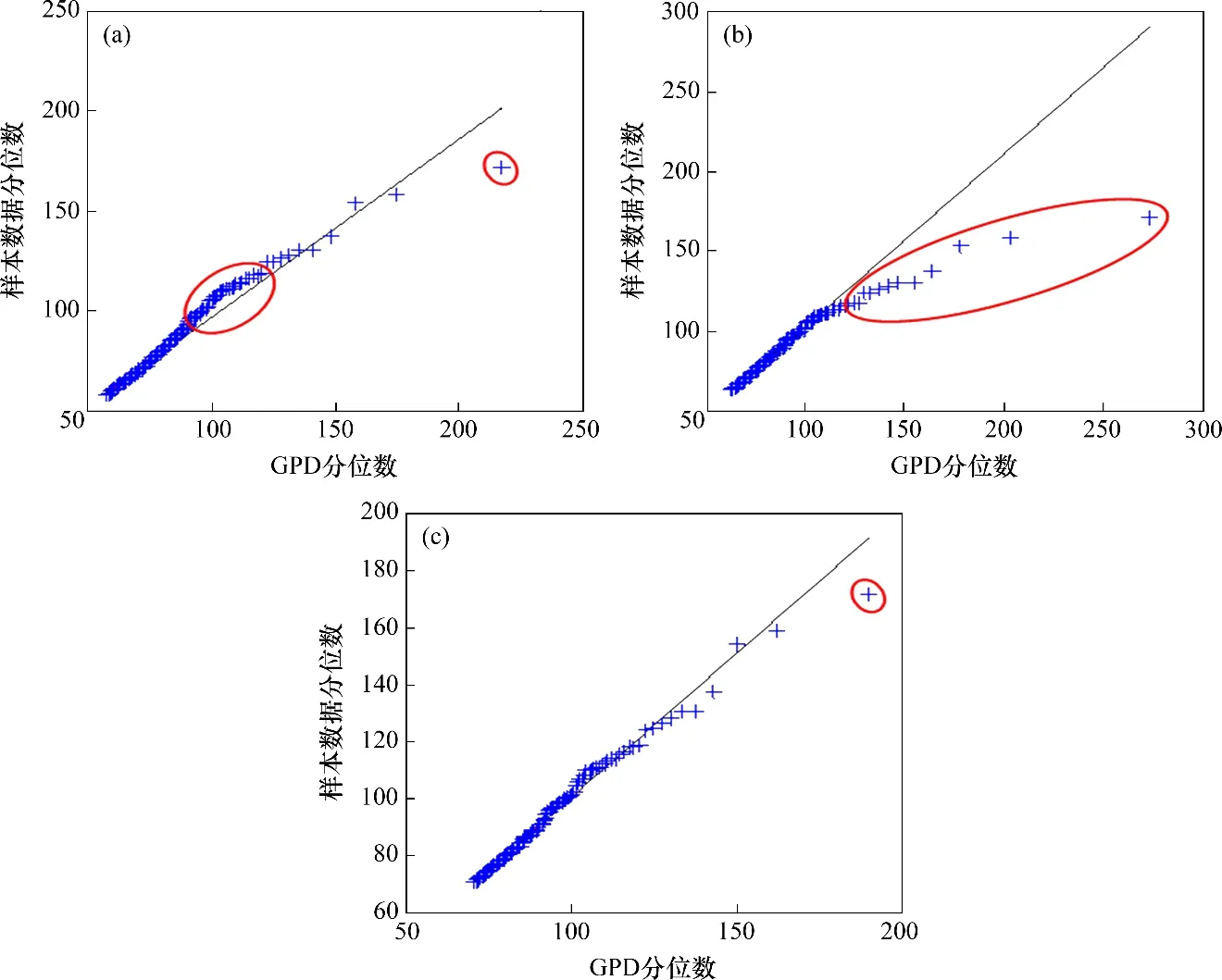
图9 不同阈值时截面3挠度GPD分布的Q-Q图Fig.9 GPD Q-Q plots of section 3’s deflection with different thresholds
2.3 可靠度评估
式(17)给出了各安装传感器截面的竖向挠度极限状态方程,式中Ri为截面i的挠度限值,本文取悬索桥设计规范[2]的挠度限值为挠度限值,每个截面都取相同的挠度限值,为3 280 mm(主跨跨度的1/250)。
表1所示为各截面竖向挠度极值分布Li的分布参数,可以根据式(17)和(18)计算7 个安装传感器截面的竖向挠度可靠度指标。图10所示为当服役时间T为100 a 时,悬索桥安装挠度传感器的各截面的可靠度指标。从图10可见:虽然悬索桥结构具有几何对称性,但是对称截面的可靠度指标存在一定差异。其原因是各截面的极值分布并不相同。最大可靠度指标出现在截面4(跨中位置),为6.3,而截面2(1/4主跨位置)和截面6(3/4主跨位置)的可靠度指标最小,2个截面的可靠度指标差别较小,分别为3.9和4.0。
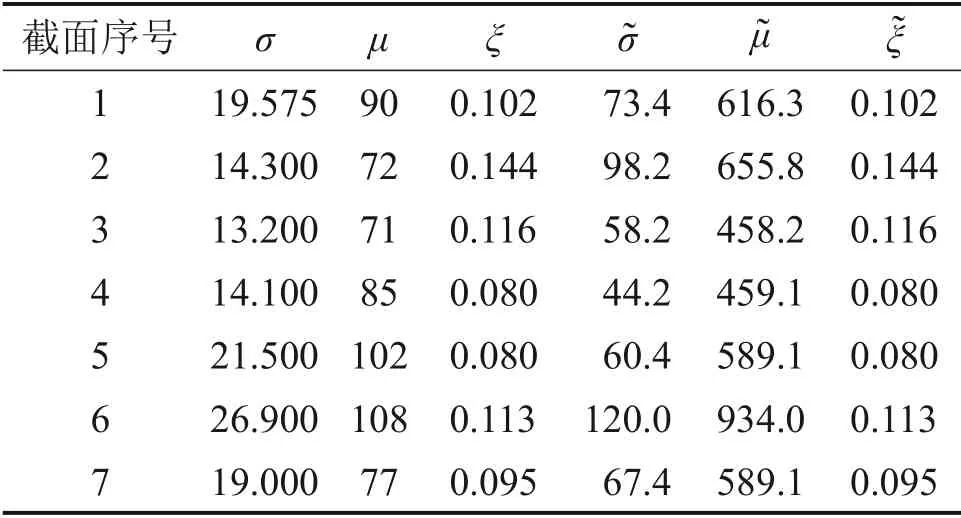
表1 GPD分布和GEVD(T=100 a)分布模型参数Table 1 Model parameters of GPD and GEVD(T=100 a)
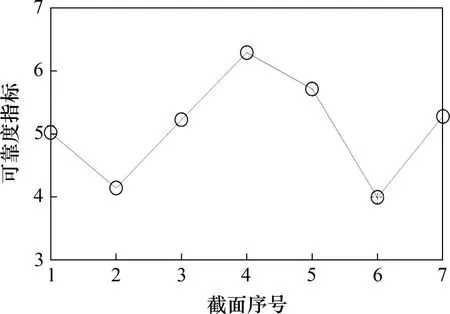
图10 悬索桥安装挠度传感器截面的可靠度指标Fig.10 Reliability indices of suspension bridge sections mounted with deflection sensors
图11所示为服役时间T从20~150 a 时的各截面可靠度指标变化情况。以图11中的计算结果为基础,计算主梁竖向挠度的体系可靠度。图6给出了式(20)计算联合失效概率所需的相关系数,采用式(19)计算体系失效概率的上下界,进而根据式(22)得到主梁竖向挠度的体系可靠度指标的上下界。图12所示为悬索桥体系可靠度指标的上下界随服役时间的变化情况,从图12可见:可靠度指标上下界十分接近,当服役时间T为100 a 时,体系可靠度指标的上下界可近似表示为βupper≈βlower=4.0,与截面2和截面6的可靠度指标十分接近,说明主梁的竖向挠度可靠性主要受上述2个截面的影响;当服役时间T为150 a时,βupper≈βlower=3.8,根据文献[25],选择目标可靠度指标为1.5,在150 a 的服役期内,该悬索桥主梁竖向挠度的可靠度均高于目标可靠度指标。
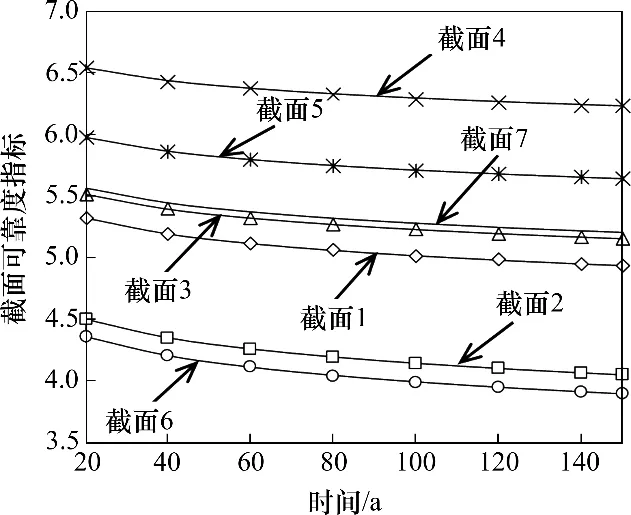
图11 安装挠度传感器截面的可靠度指标随服役时间的变化情况Fig.11 Change of reliability indices of sections mounted with deflection sensors vs service time
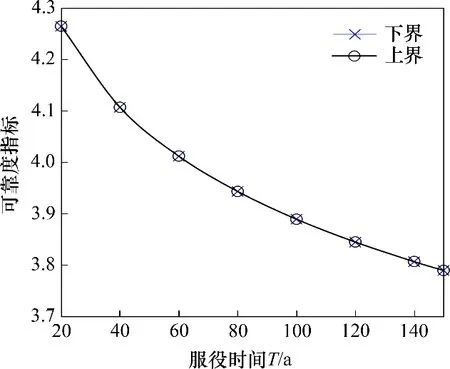
图12 悬索桥体系可靠度的上下界随服役时间的变化情况Fig.12 Change of upper and lower bounds of suspension bridges system reliability with service time
3 结论
1)建立了大跨度桥梁挠度极值分布的建模方法,采用三点比较算法提取挠度监测数据的局部极值,在此基础上基于超越阈值的极值分析方法,挠度局部极值服从GPD 分布,采用滤过泊松过程进行推导,挠度极值分布为GEVD广义极值分布。
2)提出了一种GPD分布阈值参数的确定方法。该方法综合了作图法和拟合优度检验法的优势,减小了作图法判断阈值参数的主观性。由本文方法确定的阈值参数可得到最优拟合的GPD 分布模型。
3)采用串联体系计算大跨度桥梁多个挠度监测截面的可靠度,综合考虑了多截面监测数据的随机性,避免了采用单截面挠度监测数据进行可靠度评估的盲目性。
4)针对某悬索桥开展评估方法实例研究,采用7个截面的挠度监测结果进行了可靠度评估。计算表明,体系可靠度指标的上下界较接近,当服役时间为100 a和150 a时,可靠度指标分别近似为4.0和3.8,均大于目标可靠度指标。
