基于频域对称法的磁共振数据残余噪声消除方法

2021-11-25林婷婷李玥刘大震万玲

中南大学学报（自然科学版） 2021年10期

林婷婷，李玥，刘大震，万玲

（1.吉林大学仪器科学与电气工程学院，吉林长春，130026；2.地球信息探测仪器教育部重点实验室，吉林长春，130026）

磁共振测深法（magnetic resonance sounding，MRS）自20世纪80年代末期开始逐渐发展，成为最具竞争力的地球物理勘探方法之一，它具有非侵入式直接追踪含水体分布信息的优势，被广泛应用于地下水资源探测和灾害水源勘查等领域[1-3]。然而，MRS 信号非常微弱（nV 级），探测过程易受环境噪声干扰，导致反演获取的地下水信息失真。目前的数据采集技术无法完全屏蔽环境噪声，限制了MRS 方法在复杂环境中的探测潜力[4-6]。因此，如何最大限度地消除环境噪声对MRS 信号的干扰是一个亟待解决的难题。

常见的MRS 环境噪声主要分为3 类：尖峰噪声、工频谐波噪声和随机噪声[7-9]。

1）尖峰噪声通常由物体忽然放电产生，例如太阳磁暴或静电放电。其特点是持续时间短，干扰幅度大。在数据处理过程中，大幅度尖峰噪声所在的数据段会被丢弃；对于不易识别的小幅度尖峰噪声，万玲等[10]提出了基于能量运算的尖峰噪声抑制方法进行消除。LARSEN[11]以2 个级联二阶滤波器的脉冲响应建模，专用于消除来自电网的尖峰噪声。

2）工频谐波噪声较恒定，其频率固定在电力线基频的整数倍处，通常来源于电力线、变压器等工业及生活用电。WALSH[12]开发了多通道MRS地下水探测系统，基于通道间数据相关性提出了频域自适应消噪算法。这种方法可以自动调节滤波器系数跟踪工频谐波噪声峰值位置，但其作用频率范围有限，且对参考源信号成分的单一性要求较高。之后，MÜLLER-PETKE 等[13]研究发现，设置最佳滤波器宽度并延长数据记录时间能够显著提高参考消噪方法的有效性。LARSEN等[14]提出了建模法与维纳滤波法结合来消除工频噪声。HEIN等[15]提出频域对称法，实现了MRS信号中工频噪声的进一步消除。

3）随机噪声由外界环境和仪器自身的不可预知因素产生，在统计特征上具有随机性。在实际应用中常采用叠加法来抑制随机噪声，降低了探测效率[5,16]。为此，LIN等[17-19]提出了时频峰值滤波法，可以有效抑制单次测量的随机噪声。BEHROOZMAND 等[1]总结了传统MRS 消噪流程，其中包含4个步骤：1）去尖峰噪声；2）消除工频谐波噪声；3）压制随机噪声；4）包络探测提取信号[20-22]。

采用传统MRS 消噪流程处理数据可以在一定程度上削弱各类噪声，提高信噪比。但受消噪方法原理限制，处理后的信号中仍然残余小幅度工频谐波噪声和高斯随机噪声，影响信号特征参数提取准确度。针对这一问题，本文作者在频域对称法消除工频噪声的基础上，分析该方法对残余小幅度工频谐波噪声和高斯随机噪声的抑制效果，在数据处理过程中将该方法用于压制随机噪声（第3 步），以MRS 包络信号在频域存在对称性为理论基础，对含噪MRS信号进行频域解调与时频变换，区分含噪信号的实虚分量；然后，利用工频谐波噪声的虚部分量估计实部分量，剔除后实现信噪分离。

1 基于频域对称法的MRS 探测信号消噪方法

1.1 磁共振探测地下水原理

地下水中氢质子以地磁场强度B0决定的拉莫尔频率fL绕背景场进动。磁共振方法在发射线圈中通以频率为fL的交变电流，产生与地磁场方向垂直的交变磁场。当停止激发电流后，氢质子的磁化强度不仅要围绕激发电流产生的交变磁场进动，还要逐渐回落到地磁场B0的方向上，并产生MRS信号，通过地面铺设的接收线圈获取。MRS 信号经过反演后，即可确定地下水体含水量、含水层结构、含水层深度等信息[2,23]。MRS探测方法原理图如图1所示，感应信号E的表达式为

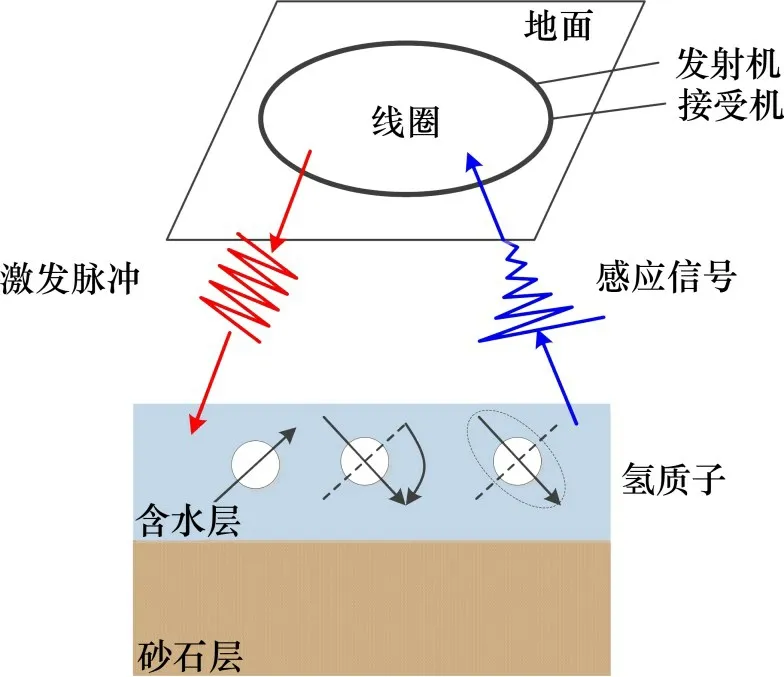
图1 MRS探测方法原理图Fig.1 Schematic diagram of MRS detection method

其中：E0为初始振幅，E0反演后可得到含水量；T2*为氢原子的弛豫时间，表征含水层介质孔隙度；φ0为初始相位，由地下电导率产生。噪声会影响信号特征参数提取准确度，导致对地下水物理信息的错误判断[24-26]。

1.2 MRS信号与工频谐波噪声频域分析

在处理MRS 数据时，通常可忽略初始相位的影响（即φ0=0）[1,26]，则磁共振信号E由式（2）和（3）所示的指数函数和余弦函数的乘积构成。

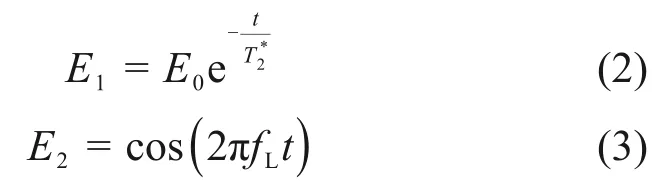
根据傅里叶变换的性质，式（1）中的傅里叶变换式等价于式（2）和（3）中的傅里叶变换形式（4）和（5）的卷积[27]。

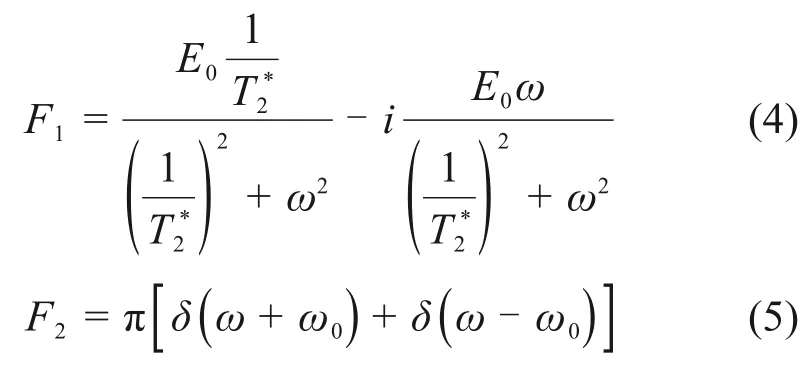
式（4）所示为MRS包络信号频谱，在复平面上实部为偶函数，虚部为奇函数，经傅里叶逆变换到时域后为纯实数信号。式（5）中ω0=2πfL，是在f=±fL处高度为的冲激函数。式（4）和（5）卷积是对式（2）的频谱调制，相当于将式（2）的频谱进行尺度变换后由f=0搬移到f=±fL处。提取信号特征参数需要对式（1）进行频谱解调（频谱调制的逆过程）获取MRS包络信号。由于包络信号频谱随|ω|增加不断趋近于0，因此，可选择有限带宽内的频谱近似解调。

首先，选择以拉莫尔频率为中心的有限带宽截取频谱；然后，将所截频谱沿频率轴左移fL个单位；最后，将频谱幅值放大2 倍，即可得到MRS包络信号频谱。设置MRS 信号的初始振幅E0=50 nV，弛豫时间T*2=100 ms，拉莫尔频率fL=200 Hz。时域信号如图2（a）中蓝色曲线所示，解调前MRS信号频谱峰值位于频率f=±200 Hz处，如图2（b）中虚线所示。解调后频谱如图2（b）中实线所示，可以看出该频谱具有式（4）所述对称性，经傅里叶逆变换得到时域MRS 包络信号为纯实数，如图2（a）中黑色实线所示，包含初始振幅E0和弛豫时间T2*的信息。

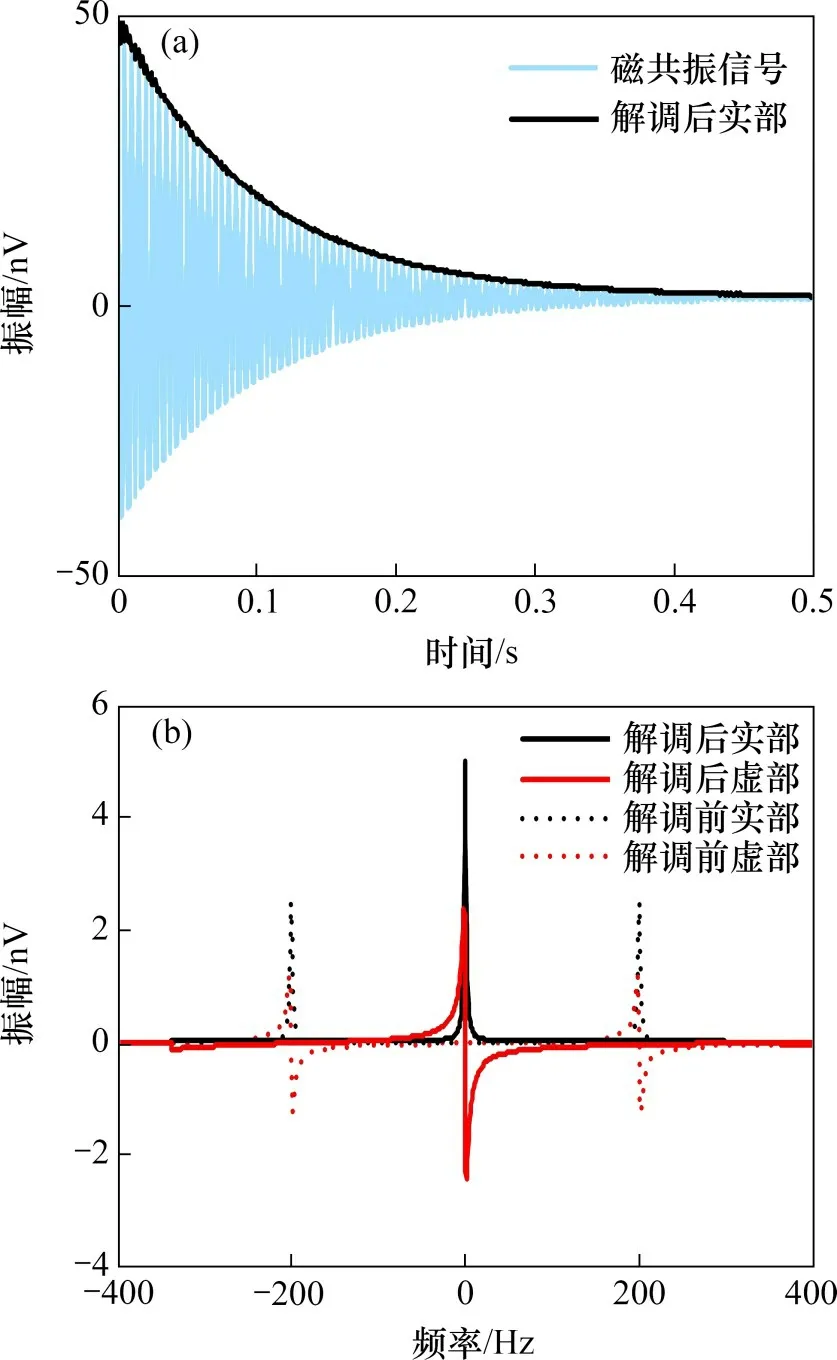
图2 仿真MRS信号和解调后MRS信号的时域图和频域图Fig.2 Time-domain and frequency-domain plots of a simulated MRS signal before and after demodulation

工频谐波噪声会破坏MRS 包络信号的频域对称性，此时，傅里叶逆变换得到的时域数据为复数，实部由MRS 包络信号和工频谐波噪声解调后的实时域分量共同构成，而虚部完全由工频谐波噪声产生。在MRS 信号中加入1 个工频噪声成分（见图3），幅度EN=10 nV，频率fN=250 Hz。图3（a）中蓝色曲线为加入工频谐波噪声的MRS信号；黑色实线为解调后实部分量，具有衰减趋势，是含噪信号的包络曲线；红色实线为工频谐波噪声解调后虚部分量。

对于频谱中f=±|fL+x|处高度为λ+μi 的工频谐波噪声，解调之后噪声峰值位于f=x处，f=-x处噪声为0，如图3（b）所示。由数学定理可知：任意函数都可以表示为1个奇函数和1个偶函数的和，且表达形式唯一[27]。则解调后的噪声可以分解为Cre，Cro，Cie和Cio共4 部分，其表达式分别为：

图3 含1个谐波成分的MRS信号解调前后的时域图和频域图Fig.3 Time-domain and frequency-domain plots of an MRS signal with a harmonic component before and after demodulation

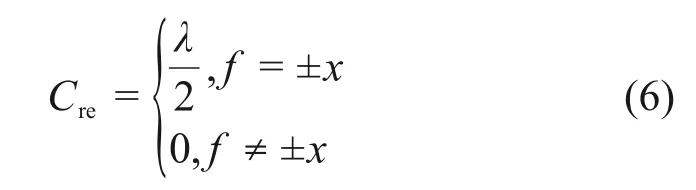
Cre和Cro以及Cie和Cio之间的区别是在f=-x处的峰值符号相反，当上述4 个分量相加时，f=-x处的噪声峰值会相互抵消，f=x处的峰值叠加产生工频谐波噪声λ+μi。Cre和Cio经傅里叶逆变换到时域后是一个纯实数序列，这就是与MRS 信号混叠在一起的工频谐噪声实时域分量，如图4（a）中黑色曲线所示。Cro和Cie经傅里叶逆变换到时域后得到纯虚数序列，也就是工频谐波噪声解调后的虚时域分量，如图4（a）中红色曲线所示。

图4 谐波噪声解调后时域图及其频谱Fig.4 Time-domain and frequency-domain plots of a harmonic component after demodulation

1.3 频域对称法消噪原理

频域对称消噪理论是基于MRS 信号的频域对称性展开研究的。首先对含噪声的MRS 数据进行傅里叶变换、频域解调、傅里叶逆变换，得到时域复数数据。该复数虚部由工频谐波噪声产生，傅里叶变换后可得到已知分量Cro和Cie。复数实部中无法直接提取工频谐波噪声实部信息，因此，对噪声虚部分量Cro和Cie在f=-x处的峰值乘-1，估计出未知的噪声实部分量Cre和Cio。然后，在频谱中f=±x处减去估计噪声峰值并进行频谱校正，再通过频谱调制和傅里叶逆变换得到消噪后的MRS信号。

频域对称法处理MRS 数据时得到的虚时域分量中包含部分高斯随机噪声，这是由于频域解调是在频谱上有限连续带宽内进行，且高斯随机噪声的无规律性决定其在变换之后产生的时域数据也是复数。虚时域分量在估算噪声实部分量之后被丢弃时，其中包含的高斯随机噪声也同时被消减。因此，频域对称法不仅可以消除工频谐波噪声的干扰，而且可以消除部分高斯噪声。在实际应用中，将频域对称法作为现有消噪流程的补充步骤，用在叠加法消除随机噪声之后，以期消除MRS 信号中仍残余的工频谐波噪声和高斯随机噪声，进一步提高信噪比。频域对称法消噪流程图如图5所示。

图5 频域对称法消噪流程图Fig.5 Flowchart of frequency-domain symmetry method

2 仿真结果及分析

为了验证频域对称法消除残余噪声的效果，在仿真MRS 信号中加入不同幅度工频谐波噪声和高斯随机噪声，仿真信号参数E0=300 nV，T*2=150 ms，fL=2 330 Hz。采用Larsen 建模法和叠加法分别消除工频谐波噪声和随机噪声，然后用频域对称法消除残余噪声，通过对比频域对称法消噪前后信噪比、初始振幅提取误差和弛豫时间提取误差对算法进行量化评估。各项评价指标的定义如下。

信噪比σSNR定义为

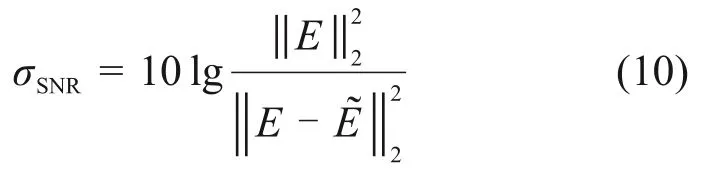
式中：E和分别为仿真信号和信号估值。

初始振幅提取相对误差σIAEE定义为

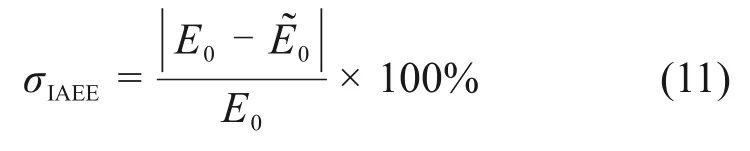
式中：为初始振幅的提取值。

弛豫时间提取相对误差σRTEE定义为

式中：为弛豫时间的提取值。

2.1 不同幅度工频谐波噪声数据处理结果

为了验证频域对称法对残余工频谐波噪声的消除效果，在MRS 仿真信号中加入10 组30～300 nV 内的工频谐波噪声AN，信噪比由23.38 dB下降到3.38 dB，每组噪声对应信噪比σSNR如表1所示。采用频域对称法处理各组数据后提取信号特征参数，所得结果均为=299.87 nV，=150.1ms，参数提取相对误差σIAEE=0.04%，σRTEE=0.07%，信噪比提高到32.49 dB。实验结果表明，即使工频谐波噪声残余很小，频域对称法也能准确消除噪声，并且在不同噪声水平下信号提取结果相同，误差很小，说明采用频域对称法消噪效果十分稳定。

表1 不同幅度工频谐波噪声下的信噪比Table 1 SNR after adding powerline harmonics with different amplitudes

图6所示为300 nV 工频谐波噪声消噪过程图。在工频谐波噪声影响下，MRS 信号上重复出现高度约为300 nV 的峰值，信号衰减趋势减弱。对含噪结果进行拟合，提取信号特征参数=247.38 nV，=259.0 ms，信噪比σSNR=3.38 dB，信号准确度严重受损。采用频域对称法处理数据。

首先，进行傅里叶变换、解调和逆傅里叶变换，由于MRS 包络信号为纯实数，因此，图6（b）中实部曲线具有明显的衰减趋势，而图6（b）中虚部曲线在水平直线附近上下震荡。2条曲线中出现的重复性峰值说明时域数据的实部和虚部均含有工频谐波噪声。然后，对实时域序列和虚时域序列进行傅里叶变换，估算工频谐波噪声实时域分量，消减后获取MRS 包络信号频谱如图6（d）黑色曲线所示。将该频谱逆傅里叶变换到时域后，包络信号指数衰减特征明显，原有重复性特征全部消除。最后，对消噪后的包络信号频谱调制，得到频域特征如图6（f）中黑色曲线所示，然后经傅里叶逆变换到时域，图6（e）中黑色曲线为消噪后MRS 全波信号。对处理后数据作非线性拟合，信号特征参数提取结果为：=299.87 nV，=150.1ms，准确度分别提高了438.5倍和1 038.1倍，信噪比提升至32.49 dB。可见，使用频域对称法消除残余工频谐波噪声可以提高提取信号准确度，其中对弛豫时间准确度的影响最显著。

图6 300 nV工频谐波噪声消噪过程图Fig.6 Process of eliminating powerline harmonic noise with an amplitude of 300 nV

2.2 不同幅度随机噪声数据处理结果

为了验证频域对称法对残余随机噪声的消除效果，在MRS 仿真信号中加入13 组0～60 nV 内的高斯随机噪声，对比消噪前后的特征参数提取结果和相对误差，判定频域对称法消除残余高斯随机噪声的有效性，如图7所示。从图7可以看出：采用频域对称法消噪之后，特征参数提取结果更加接近仿真值，信号提取误差变小。当残余高斯随机噪声很小（5 nV）时，采用频域对称法消噪后，初始振幅E0由298.41 nV 提高到299.37 nV，初始振幅提取相对误差由0.53%降低到0.21%，弛豫时间T*2由152.4 ms降低到151.1 ms，弛豫时间提取相对误差由1.61%降低到0.71%，信噪比由21.34 dB提高到24.77 dB。说明在高斯随机噪声残余较小的情况下，频域对称法也能将其消除，改善MRS 信号的提取质量。

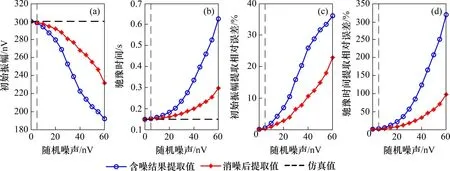
图7 不同幅度高斯随机噪声水平下提取信号结果Fig.7 Signal fitting results after adding random noise with different amplitudes

2.3 仿真数据处理结果

为了验证频域对称法作为现有消噪流程补充步骤的必要性，仿真9 组16 次采集的MRS 数据，假设数据中尖峰噪声已经被消除，工频谐波噪声和随机噪声分别在3 000 nV 和100 nV 以内渐增式随机产生。采用建模法、叠加法和频域对称法依次消除工频谐波噪声、随机噪声和残余噪声，其中1 组消噪结果如图8所示。图8中蓝色曲线是采用建模法对单次数据直接消除工频谐波噪声后的处理结果，绿色曲线是建模法和叠加法共同消除噪声之后的结果，红色曲线是进一步采用频域对称法消除残余噪声后的结果。频域对称法消除残余噪声后，全波信号衰减趋势更强，包络信号拟合结果更接近仿真信号包络曲线，信噪比由15.29 dB提升至19.33 dB，初始振幅提取相对误差由2.03%减小为0.86%，弛豫时间提取相对误差由5.53%减小为2.27%。因此，在传统消噪流程之后增加频域对称法可以消除残余噪声，进一步提高信噪比和特征参数提取准确度，改善提取MRS信号的质量。图9所示为MRS 信号的三维时频分布图，经建模法、叠加法和频域对称法处理后的数据，噪声极大程度被消除，MRS信号成分有效保留。

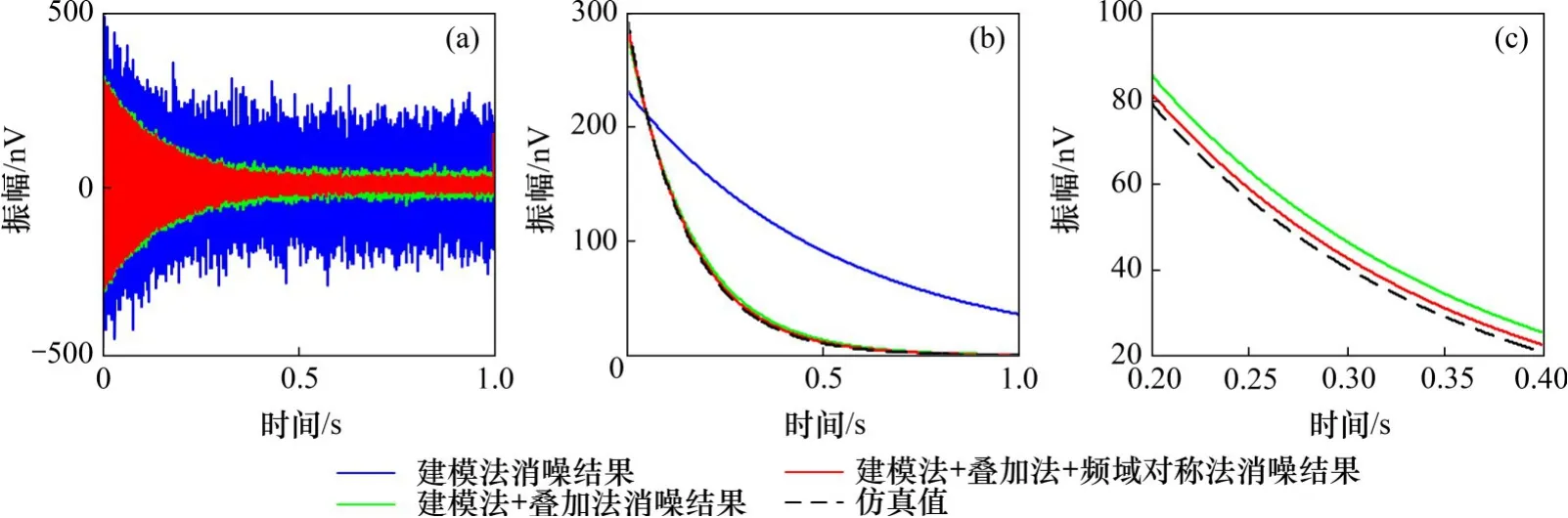
图8 仿真数据处理结果时域图Fig.8 Time-domain plot of simulated processing results

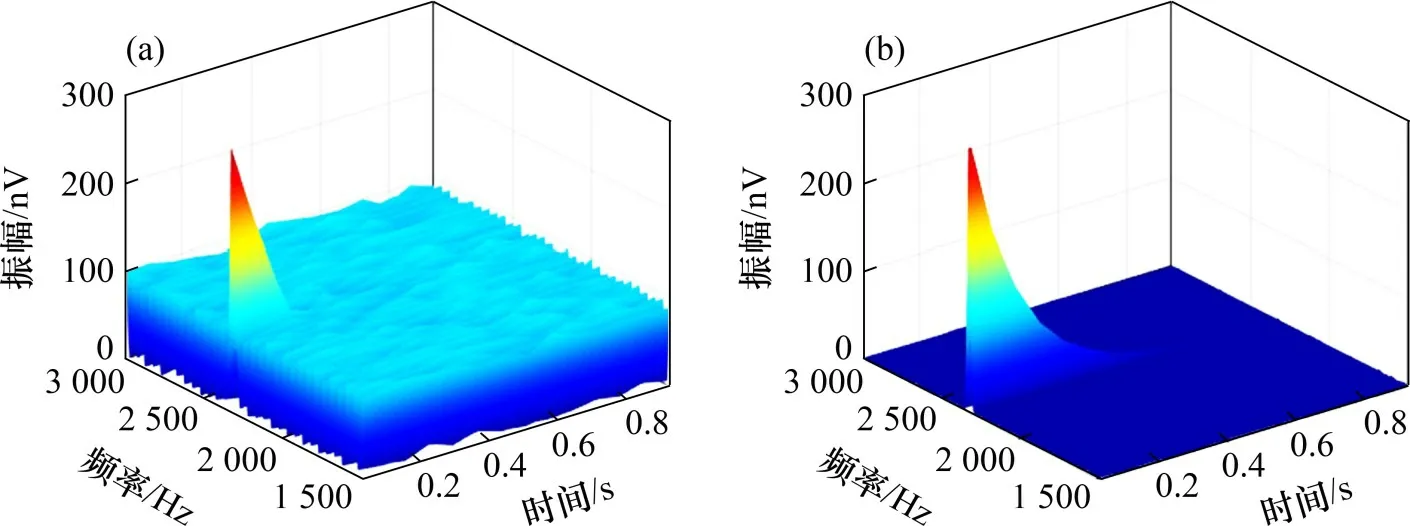
图9 仿真数据处理结果三维时频图Fig.9 Time-frequency domain of simulated processing results

表2所示为使用不同方法处理仿真数据后的特征参数提取情况和信噪比。从表2可以看出：频域对称法参数提取结果优于建模法参数提取结果，信噪比平均提高4.23 dB，但在建模法中加入叠加法消除随机噪声之后，提取信号准确度高于单独使用频域对称法消噪时的信号准确度，信噪比平均提高7.81 dB，若在叠加法之后加入频域对称法，信号质量会得到进一步改善，信噪比平均提高3.78 dB。因此，本文提出的频域对称法不宜单独使用，而应当作为传统消噪流程的补充步骤，消除MRS 信号中残余的工频谐波噪声和随机噪声，进一步提高信噪比。

表2 使用不同方法处理仿真数据后的特征参数提取情况和信噪比Table 2 Parameter fitting and signal-to-noise ratio after processing simulated data using different methods

3 实测数据处理

为了验证本文提出算法的实用性，采用自主研制的MRS 地下水探测仪[1]在长春市烧锅镇采集数据。当地拉莫尔频率fL=2 337 Hz。3 组发射脉冲矩Q在0.99～1.84 A·s 之间均匀分布。采样频率fs=25kHz，采集时间256 ms，每组脉冲矩叠加16次。

对实测数据进行尖峰噪声处理后，得到3个脉冲矩信号的处理结果如图10中灰色曲线所示，信号完全淹没在工频谐波噪声和随机噪声中。采用建模法和叠加法分别消除工频噪声和随机噪声，数据处理结果如图10中红色曲线所示，可以看出实测数据中大部分噪声被压制，信号初见衰减趋势，但数据中仍有部分噪声残留，Q为0.99，1.46 和1.84 A·s 时脉冲矩信号的信噪比σSNR分别为-3.95，-4.14和-4.31 dB。信号特征参数E0分别为382.13，383.30 和397.62 nV，T*2分别为259.9，380.0 和348.4 ms。进一步采用频域对称法消除残余噪声，结果如图10中黑色曲线所示。时域信号衰减趋势更明显，频域中红色残余噪声被消除，信号峰谱更突出，计算Q为0.99，1.46 和1.84 A·s时脉冲矩信号的信噪比σSNR分别为-1.36，-0.61和-0.83 dB。信号特征参数E0分别为252.63，330.12和286.49 nV，T*2分别为169.9，168.5 和174.9 ms。相比于频域对称法消噪之前，3个脉冲矩信号的信噪比增量分别为2.59，3.53 和3.48 dB，初始振幅和弛豫时间提取准确度均有所提高。