基于时延估计的绳驱动飞行机械臂模糊非奇异终端滑模飞行控制

孟思华，王尧尧,2，陈柏，吴洪涛

（1.南京航空航天大学机电学院，江苏南京，210016；2.浙江大学流体动力与机电系统国家重点实验室，浙江杭州，310027）

随着多旋翼飞行器的研究和应用的拓展，飞行机械臂系统逐渐得到研究者的广泛关注[1-2]。在早期的飞行机械臂研究中，研究者在飞行器底部安装简单的机械手爪来完成抓取或搬运任务，这种机械手抓结构简单，质量较小，对飞行器控制影响较小[3-5]。然而，这些飞行机械臂缺少灵活的机械臂系统，难以完成更复杂精细的任务。其后，研究者在飞行器上安装机械臂（例如，瑞士苏黎世联邦理工大学与美国内华达大学合作研制的旋翼飞行并联机械臂[6]、奥克兰大学研制的树冠层采样飞行机械臂[7]）以获得灵活操作的能力。国内的飞行机械臂（例如，东南大学研制的重心调节飞行机械臂等[8]）研究起步较晚，但也取得了一定的成果。

在保证机械臂作业能力的条件下降低运动部分的质量是飞行机械臂设计面临的一大难题。传统的机械臂将驱动电机和减速器安装于机械臂关节处，增大了机械臂运动部分的惯性，而飞行机械臂是无根系统，机械臂的运动将对系统造成很大扰动。一种有效的解决方法是采用绳驱动技术。引入绳驱动技术的机械臂，其驱动单元安装在机械臂底座，通过绳索传递力和运动，大大降低了机械臂运动部分的质量[9-11]。目前，绳驱动技术主要应用于陆上的机器人系统以及部分水下机器人系统，很少应用于飞行机械臂系统。考虑到绳驱动技术的优异特性以及飞行机械臂控制性能与飞行器-机械臂质量比之间的矛盾，绳驱动技术在飞行机械臂领域具有极高的应用和研究价值。因此，本文拟设计一种新型绳驱动飞行机械臂系统。

针对飞行机械臂系统，研究者主要提出了2种控制策略：线性控制策略[12-13]以及非线性控制策略。线性控制策略在平衡点附近具有良好的控制性能，但机械臂运动导致系统偏离平衡点时很难稳定，为此，众多学者更加关注非线性控制策略[14-16]。滑模变结构控制（SMC）因其鲁棒性好、对系统参数不敏感等特点得到广泛应用[17-20]。终端滑模控制器具有在平衡点附近收敛较快的特点，更适用于飞行机械臂场景。

飞行机械臂本身为一个复杂的高耦合系统，其精确建模是一个难题。绳驱动飞行机械臂同时具有绳驱动机械臂的非线性特性和机械臂与飞行器的高耦合特性，其精确建模难度极大。目前常用的建模方法主要有整体建模法和独立建模法[21-22]。但这2 种方法都无法有效地解决动力学参数时变以及系统的复杂非线性问题以获得良好的控制性能。

时延估计控制（TDC）是一种不基于模型的控制策略，其关键技术为时延估计技术（TDE）[23]。利用时延信号估计系统动力学，可极大地缓解建模难、建模不精确带来的控制难题。时延估计控制已广泛应用于各领域，例如语音增强、状态与参数估计以及非线性控制等[24-26]。考虑到绳驱动飞行机械臂系统建模的困难，时延估计技术将在此场景下拥有广阔的应用前景。

综合现有成果，本文作者通过引入绳驱动技术，提出一种新型绳驱动飞行机械臂系统。针对所提飞行机械臂系统，设计基于TDE 的模糊非奇异终端滑模控制器，并进行稳定性与收敛性分析。最后，为验证所提出的控制器的有效性，进行仿真对比实验。

1 飞行机械臂系统结构

本文设计的飞行机械臂系统主要由四旋翼飞行器和机械手2部分组成。采用绳驱动技术的机械臂，将驱动单元安装在机械臂的底部，通过绳索将运动和力传递到关节处，大大降低机械臂移动部分的质量，极大地削弱机械臂运动对飞行平台的影响，降低飞行机械臂系统控制难度。

图1所示为基于绳驱动机械臂的新型飞行机械臂系统。所设计的飞行机械臂总质量为3 kg。所选飞行平台为四旋翼飞行器，轴距为530 mm。绳驱动机械臂具有3 个自由度，长度为421 mm，总质量为875 g。绳驱动机械臂的驱动电机被安装在底座上，通过细钢缆传递动力，机械臂移动部分不再含有驱动电机以及减去器等机构，质量为375 g，不足机械臂部分总质量的一半。而其承载能力并未降低，有效缓解了飞行器-机械臂质量比与作业能力以及控制品质之间的矛盾。

图1 飞行机械臂系统结构Fig.1 Structure of aerial manipulator

2 动力学建模

飞行机械臂系统的坐标系如图2所示。飞行机械臂的坐标系系统可以分成4个部分：固连于地面的惯性坐标系{Oi}、固连于飞行器对称中心的机体坐标系{Ob}、机械臂关节坐标系{Oj}以及末端执行器坐标系{Oe}。飞行机械臂姿态可以表示为Φ=[ϕ,θ,ψ]T，其中ϕ,θ和ψ分别为翻滚角、俯仰角和偏航角。旋转矩阵表示的姿态为

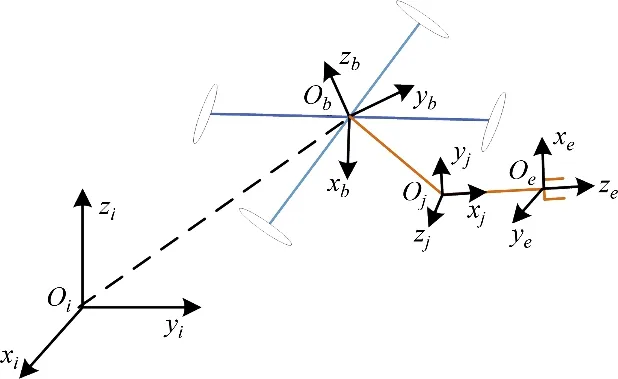
图2 飞行机械臂坐标系Fig.2 Reference frames for an aerial manipulator

式中：c表示cos；s表示sin。

采用独立建模方法利用牛顿欧拉法建立飞行机械臂的动力学模型，如下式所示[27]：

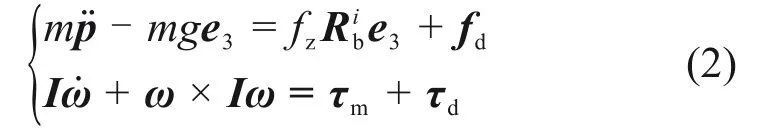
式中：m为飞行机械臂质量；I为飞行机械臂惯性张量；p为位置向量，p=[x,y,z]T；ω为机体角速度；e3为惯性系中的单位向量，e3=[0,0,1]T；fz为旋翼在机体坐标系下产生的总拉力；fd为机械臂与飞行器的耦合力以及复杂外部扰动；τm为旋翼在机体坐标系下的力矩，τm=[τx,τy,τz]T；τd为机械臂与飞行器的耦合力矩以及复杂外部扰动。τ和fz如下式所示：

式中：cT为旋翼升力系数；cM为旋翼扭矩系数；ωi为第i个旋翼的转速；d为旋翼到飞行器中轴线距离。

模型中没有考虑到飞行机械臂的动力学时变，但其作用不可忽视，动力学参数变化为

式中：m0和I0为静态动力学参数；Δm和ΔI为由外部扰动以及机械臂作业引起的动力学参数变化。为补偿动力学参数时变，引入TDE 技术，飞行机械臂动力学方程可写为：

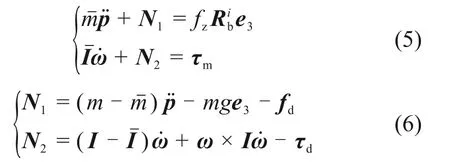
式中：和为常量。

可知N1和N2形式非常复杂，难以计算，但可使用时延估计技术获得足够精确的估计值。

3 控制器设计及稳定性分析

对于飞行机械臂系统，通常将飞行平台作为运动的主体，而机械臂主要用来调整末端执行器的姿态。本文主要对飞行平台的控制进行研究，所设计控制器结构如图3所示。

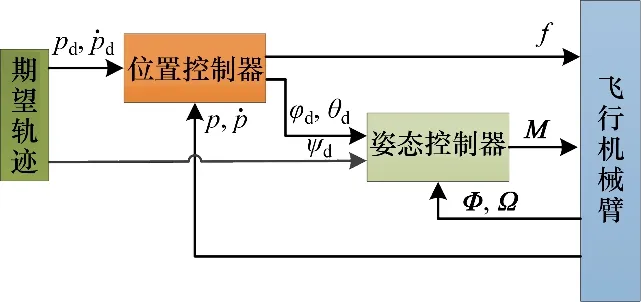
图3 飞行机械臂控制系统结构Fig.3 Control structure for aerial manipulator

3.1 姿态控制器设计及稳定性分析

3.1.1 姿态控制器设计

非奇异终端滑模控制器（NTSM）[28]如下式所示：

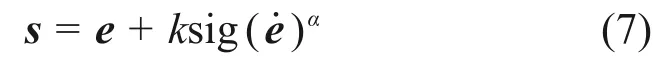
式中：k＞0；sig（）α=||αsign（）。飞行器姿态误差定义为

式中：Φd为姿态期望；Φ为当前姿态。所设计控制器滑模面为

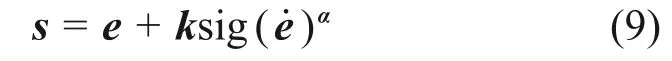
式中：s∈R3；k=diag（k1,k2,k3）；1＜α1＜2，1＜α2＜2，1＜α3＜2。所选趋近律为

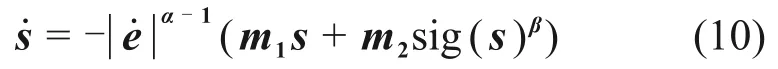
式中：m1=diag（m11,m12,m13）,m1i＞0；m2=diag（m21,m22,m23）,m2i＞0；0＜βi＜1。

由式（9）及式（10）可得误差加速度为

由式（5）、式（8）以及式（11）得姿态环控制器为

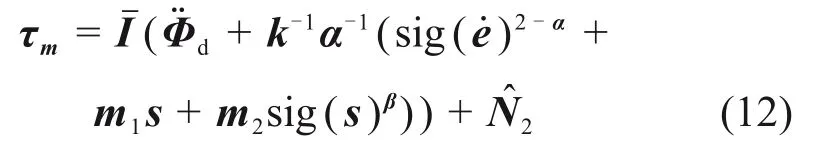
3.1.2 稳定性及收敛性分析

引理1由李雅普诺夫稳定性判据，若V（x）≥0且满足：

则V（x）将在如下有限时间内从V（x0）收敛到V（0）：

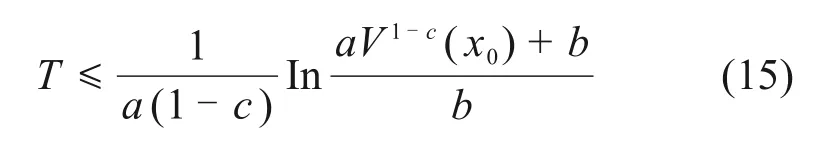
式中：a＞0;b＞0;0＜c＜1。

证明1控制器中引入了TDE 技术，考虑TDE误差的实际控制器输出可表示为

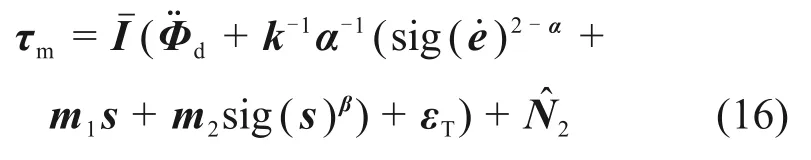
为方便起见并不失一般性，此处仅考虑一个姿态角的稳定性分析。取V（si）=si2/2，由式（10）可得

将式（17）右边第一项和第三项结合，有

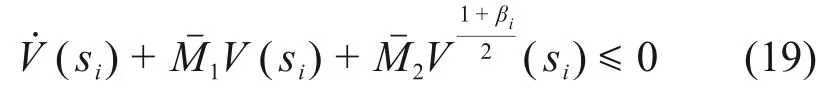
由式（19）及引理1，V（si）将持续趋向V（0）直到≤0 或≤0。即若≠0，si将收敛到如下区域：

同理，将式（17）右边第二项和第三项结合可得

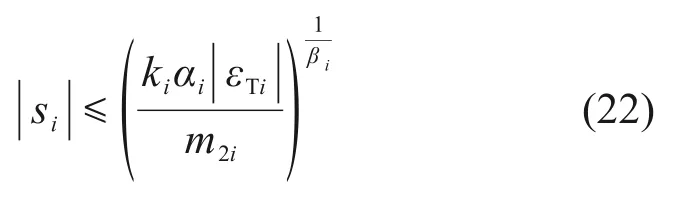
即≠0时，si将收敛到如下区域：

若|si|＞B，则由式（24）及式（25）可知≠0，即si将继续收敛。综上所述，si将收敛到|si|≤B。滑模面方程可以写为

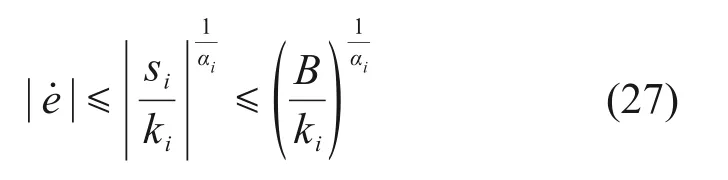
最后，将式（23）及式（27）代入滑模面方程，可得误差绝对值上界：

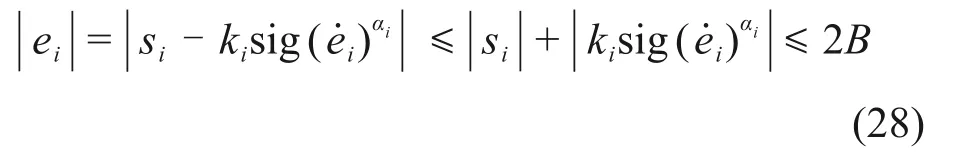
3.1.3 模糊控制器

由式（12）可知，选择较小的k，系统将会更快收敛，然而，这将导致系统抖动。为了获得更快的收敛速度以及保证系统的控制品质，引入模糊控制器（FLS）实时调节参数。引入FLS的控制器为

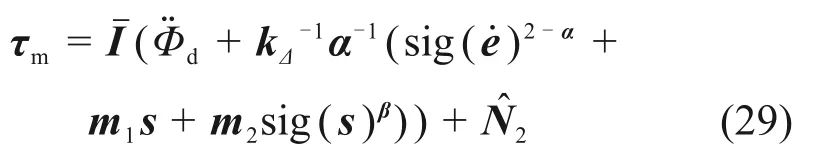
式中：kΔ=k（1+Δ）；Δ为FLS 输出。当姿态由于未知扰动而偏离期望值或误差接近于0时，FLS实时调整参数以获得最佳效果。

所设计FLS 有2 个输入和1 个输出，根据其值映射到7个三角形模糊区域的隶属度函数上。去模糊方法为重心法。输入的模糊语言值选择为NL，NM，NS，ZO，PS，PM 和PL。FLS 的输出为负值，其模糊值选择N1，N2，N3，N4，N5，N6和N7。

图4所示为FLS 决策平面。从图4可见：当误差绝对值较大时，FLS输出越小；当误差与误差导数同号且较大时，FLS输出最小；当误差与误差导数都接近0时，FLS输出最大。

图4 姿态环Fuzzy决策面Fig.4 Surface of Fuzzy of attitude controller

3.2 位置控制器设计

位置控制器滑模面、趋近律与姿态控制器相同，同理可得到位置环控制器输出为

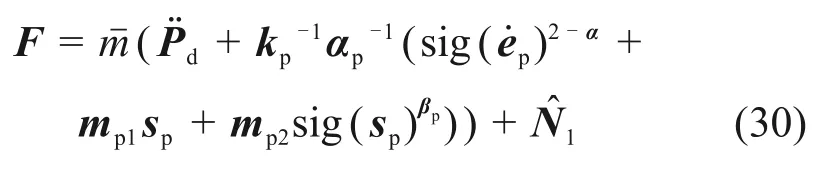
式中：为常量；Pd为位置期望；为TDE输出；下标p表示其为位置环控制参数。对位置环控制器稳定性和收敛性的分析与对姿态环的分析相同。引入FLS的位置环控制为

位置环控制器的FLS决策平面如图5所示。

图5 位置环Fuzzy决策面Fig.5 Surface of Fuzzy of position controller

飞行器位置控制通过姿态控制实现，由式（5）、式（30）及式（31）可得

式中：F为位置环控制器输出，F=[f1,f2,f3]T。给定航向角期望ψd并限制各姿态角范围如下：

可解得姿态角期望如下式所示：

4 仿真分析

为了提高仿真速度，对模型进行合理简化，简化后的模型如图6所示。飞行机械臂及旋翼参数为mb=1.89 kg，Ibx=Iby=0.074 3 kg·m2，Ibz=0.147 kg·m2，cT=1.486×10-7N/（r·min-1），cM=2.925×10-9N·m/（r·min-1）。机械臂有2 个自由度，连杆的参数为ml=120 g，Ilx=11154 kg·mm2，Ilx=11154 kg·mm2，Ilx=11154 kg·mm2，l=0.1m。使用simulink的simmechanics工具箱导入solidworks模型即得仿真所需动力学模型。

图6 飞行机械臂简化模型Fig.6 Simplified model of aerial manipulator

本文进行5组仿真。其中，仿真1为机械臂运动与否2 种工况下SMC+TDE 控制器效果的对比，说明提出一种新的鲁棒控制策略的必要性；仿真2及仿真3 分别对比SMC+TDE，NTSM+TDE 以及NTSM+TDE 与所提控制器的控制效果；仿真4 在仿真3的基础上增加对升力的扰动，扰动为第10 s时的脉冲信号，对比3 个控制器对扰动的鲁棒性；仿真5在阶跃轨迹下对比SMC+TDE，NTSM+TDE以及所提控制器的响应速度，验证所提控制器的快速性。仿真1～4所选轨迹分别为pdx=-0.5，pdz=0.2t，ψd=rad，仿真5 所用阶跃轨迹为pdx=1，pdy=1，pdz=1，ψd=0。

为有效对比控制器效果，3个控制器所选用控制参数相同，其位置控制器参数为：kp=[2,2,2]T，αp=[1.2,1.2,1.2]T，βp=[0.6,0.6,0.6]T，mp1=[1,1,4]T，mp2=[4,4,7]T，mˉp=[0.03,0.03,0.2]T。姿态控制器参数为：k=[0.8,0.8,0.8]T，α=[1.6,1.6,1.6]T，β=[0.6,0.6,0.6]T，m1=[12,12,12]T，m2=[12,12,12]T，Iˉ=[0.1,0.1,0.02]T。仿真采样时间为1 ms，时延估计延时时间均为1 ms。线性滑模的参数β为[1,1,1]T。绳驱动机械臂关节的轨迹均为π sin（πt）/3。

仿真1图7所示为仿真1 误差对比，图8所示为仿真1 轨迹曲线。由图7和图8可见：采用线性滑模控制器的飞行机械臂，机械臂运动将导致跟踪误差增加；机械臂不运动时，y轴位置误差的绝对值最大值小于4.3 cm，均方误差为1.379 8 cm；机械臂运动时，位置误差的绝对值最大值大于6 cm，并且波动程度很大，均方误差为2.071 1 cm。而x轴和z轴在2 种情况下具有相似的控制精度，这是由于机械臂在YOZ平面内运动，其影响主要在y轴和z轴上。而从z轴误差放大图可看出机械臂运动的影响。从y轴误差及波动情况可以了解到线性滑模控制器在简单的四旋翼控制方案中具有可接受的控制性能，但在飞行机械臂场景中，机械臂运动引起的扰动无法得到很好的补偿，因此，需要设计一个能够补偿机械臂扰动的控制器。

图7 仿真1误差对比Fig.7 Error comparision of simulation 1

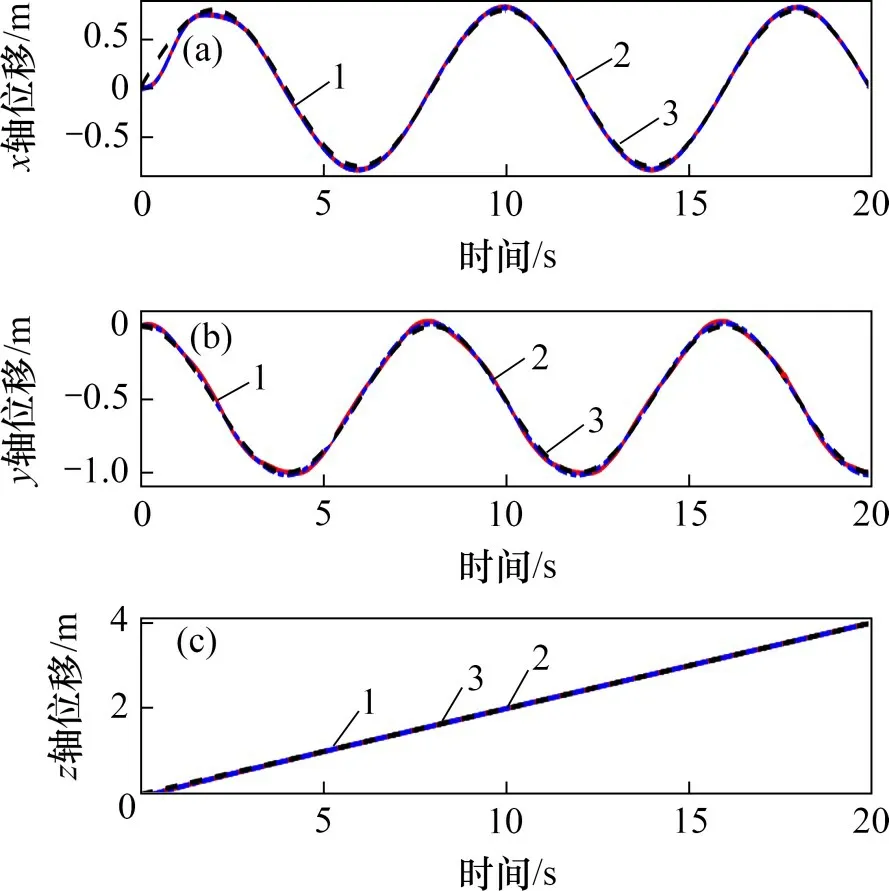
图8 仿真1轨迹对比Fig.8 Trajectory comparision of simulation 1

仿真2图9所示为仿真2误差对比，图10所示为仿真2轨迹曲线。线性滑模控制器在y方向上位置误差绝对值最大为4 cm，均方差为2.023 5 cm，而非奇异终端控制器的误差绝对值最大为3 cm，均方差为1.599 1 cm。另外，非奇异终端控制器的收敛速度和跟踪误差比线性滑模控制器的小。然而，注意到在x方向和z方向上，在开始的几秒钟，非奇异终端控制器的误差比线性滑模控制器的误差大。非奇异终端控制器在误差较小的情况下具有快速收敛的特性，而在误差较大的情况下没有特别的设计。针对这一问题，设计具有模糊推理系统的终端滑模控制器。

图9 仿真2误差对比Fig.9 Error comparision of simulation 2

图10 仿真2轨迹对比Fig.10 Trajectory comparision of simulation 2

仿真3图11所示为仿真3 误差对比，图12所示为仿真3 轨迹对比。从图11和图12可以看出：所提控制器在初始阶段的收敛速度相比非奇异终端控制器得到很大提高，而且其跟踪误差较小，所提控制器在x，y和z轴上的误差均方差分别为4.502 5，1.642 8 和1.694 1 cm，而非奇异终端控制器的误差均方差分别为6.300 1，1.599 1和2.306 cm，并且在开始几秒的误差收敛较快。从以上仿真结果可以看出，所提控制器的综合性能比非奇异终端滑模和线性滑模控制器的综合性能优。

图11 仿真3误差对比Fig.11 Error comparision of simulation 3

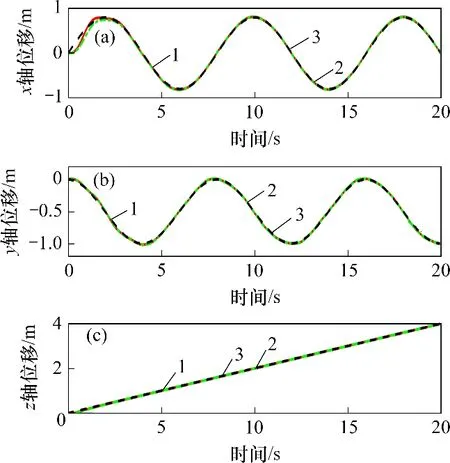
图12 仿真3轨迹对比Fig.12 Trajectory comparision of simulation 3

仿真4图13所示为仿真4 误差对比。图14所示为仿真4 轨迹曲线。仿真4 的工况与仿真3 的工况相同，仅在第10 s时在飞行平台的2个旋翼上增加脉冲力扰动，模拟阵风对飞行机械臂的扰动，脉冲力持续时间为0.2 s，幅值为5 N。从图13可以看到：在第10 s时，飞行器位置误差随脉冲扰动而增大，但最大误差由小到大的顺序以及误差收敛速度由大到小对应的控制器均为所提出的控制器、NTSM+TDE 和SMC+TDE，说明了所提控制器对扰动的鲁棒性。

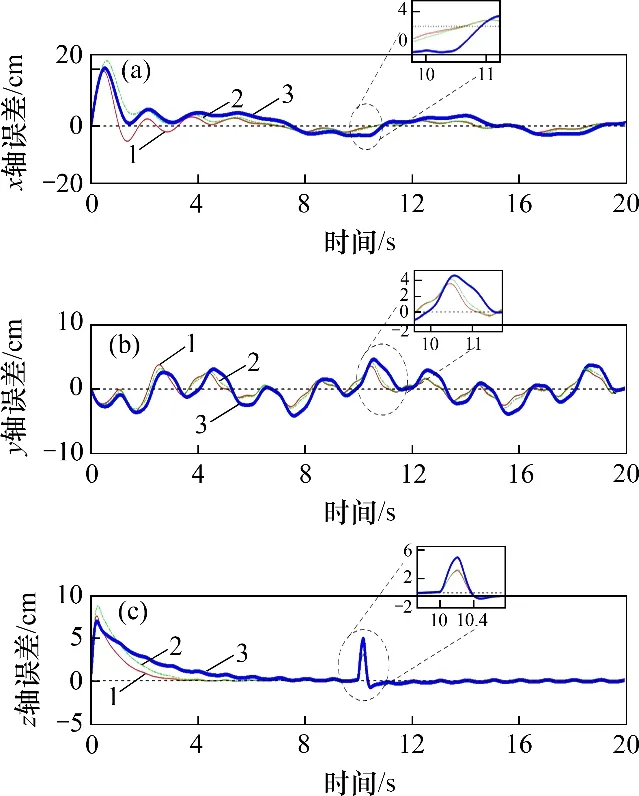
图13 仿真4误差对比Fig.13 Error comparision of simulation 4

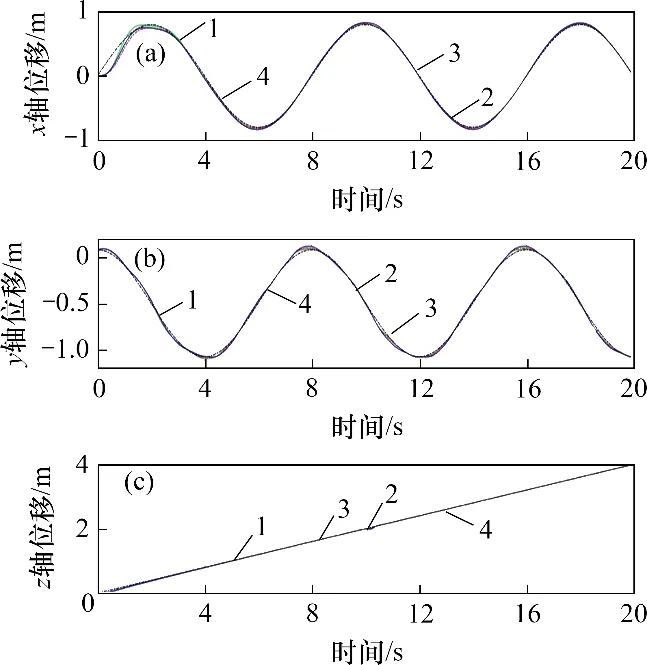
图14 仿真4轨迹对比Fig.14 Trajectory comparision of simulation 4

仿真5图15所示为仿真5误差对比。根据收敛速度由快到慢，控制器的顺序依次为所提出的控制器、非奇异终端控制器和线性滑模控制器。另外，所提控制器的跟踪误差最小。非奇异终端控制器与线性滑模控制器在仿真的初始阶段的收敛速度没有显著差异，而由于模糊推理系统的引入，所提控制器在仿真初始阶段的收敛速度提高。

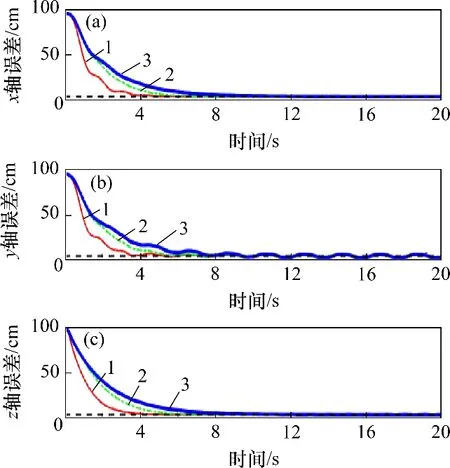
图15 仿真4误差对比Fig.15 Error comparision of simulation 4

5 结论

1）提出了一种基于绳驱动技术的飞行机械臂。采用绳驱动技术的机械臂，其驱动电机安装在机械臂的底座，减少了机械臂运动部分的质量，从而降低了对机械臂运动对机体的干扰，进而保证了更强的作业能力。

2）设计了基于时延估计技术（TDE）的模糊非奇异终端滑模控制器（NTSM）。该控制器分为3部分：TDE，NTSM 和FLS。通过TDE 技术避免建模难、建模不精确的问题，通过NTSM 控制器，保证了系统在干扰和TDE 误差下的良好性能，保证了飞行机械臂场景下误差的收敛速度。最后，利用FLS对NTSM 控制器的参数进行调整，提高了控制品质。仿真结果表明，该控制器在飞行机械臂场景下具有优异的鲁棒性。