基于COMSOL的线聚焦EMAT声场特性仿真分析*
2021-11-24潘奕宏吴运新吴雨唐
潘奕宏, 吴运新, 吴雨唐, 蔡 壮
(1.中南大学 轻合金研究院,湖南 长沙 410083; 2.中南大学 高性能复杂制造国家重点实验室,湖南 长沙 410083)
0 引 言
电磁超声换能器(electromagnetic acoustic transducer,EMAT)无需耦合剂,能够克服高温、被测物表面粗糙等极端工况,实现快速在线检测,被广泛应用于材料测厚和缺陷检测等领域[1~5]。为了提高EMAT的换能效率和信噪比,国内外研究人员从提离敏感性、改善磁通路、电路匹配、线圈的优化设计等不同方面进行了研究[6~9]。为了进一步增强EMAT的检测效果,提高微小裂纹或点状缺陷的检测精度,研究人员通过线聚焦或点聚焦的方式提高EMAT的性能[10~15]。其中,Ogi团队[10,11]提出了线聚焦型EMAT,其采用改变匝间距的曲折线圈设计,成功检测到0.05 mm深的缝隙。文献[12]应用双曲折线圈,设计出单侧辐射的线聚焦EMAT,增强了聚焦侧的超声波信号幅值。于腾飞[15]对聚焦型换能器的永磁体尺寸进行了优化设计,并设计了配套使用的电磁超声检测平台硬件系统。对于聚焦型EMAT,要求在设计的焦点处有更高的信号幅值和更集中的声聚焦能量分布,因此,在设计聚焦型EMAT的过程中也需要考虑其声场特性[13]。然而,针对线聚焦EMAT的关键参数对其超声信号幅值和声场能量分布的研究尚不深入和完善。
本文将换能器激发过程视为一个整体,建立了线聚焦EMAT的二维有限元时域模型,研究了线聚焦EMAT所激发超声波的声场特性,分析了激励周期、聚焦距离和线圈匝数对线聚焦主瓣峰值和声束宽度的影响,揭示换能器关键参数对其线聚焦性能的作用规律,对指导实际的应用过程具有重要意义。
1 线聚焦EMAT工作原理及线圈几何构型
本文重点关注线聚焦EMAT作用于铝合金的情况,因此只考虑洛伦兹力的作用。图1(a)所示为换能器工作原理示意图,换能器主要包括三部分:提供偏置磁场的永磁体、承载大功率交变电流的曲折线圈和被检测的铝合金试块。曲折线圈相邻导线电流流向相反且导线间距连续变化,当大功率交变电流流过曲折线圈时,根据法拉第感应定律,交变电流产生动态磁场,时变动态磁场在铝合金试块趋肤层内诱导出感应涡流,感应涡流与偏置磁场相互作用产生洛伦兹力,质点在洛伦兹力的作用下进行周期往复的高频振动,当电流激励频率大于20 kHz时,就会在试块内部激发出超声波。
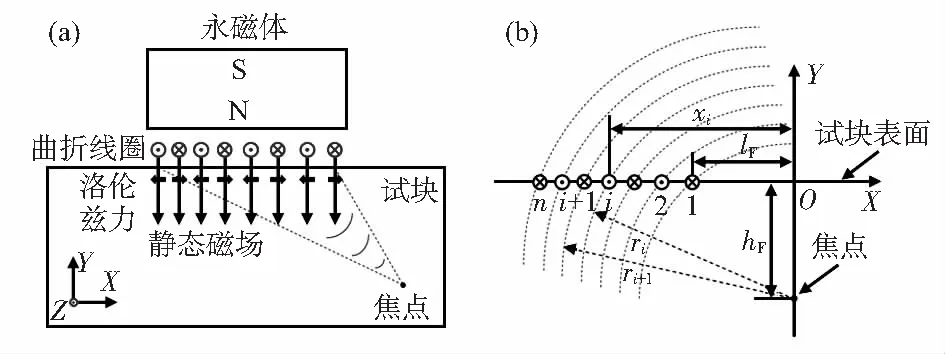
图1 线聚焦EMAT工作原理及线源位置示意
图1(b)是确定线聚焦EMAT曲折线圈导线位置的示意图,hF定义为聚焦深度,lF是第一根线源到坐标原点的距离,定义为聚焦距离,是线圈的重要设计参数之一。在实际应用设计时,首先要根据工程需要选定聚焦深度和电流激励频率,然后再对线圈的结构工艺参数进行设计。对于选定的的激励频率f和聚焦深度hF,聚焦距离lF和线圈匝数n可以选取不同的值,为使铝块内部传播的超声波产生聚焦,第i+1根线源和第i根线源到焦点的声程差应满足超声波半波长关系,第i根线源的位置可由如下式子计算
ri+1-ri=c/2f
(1)

2 线聚焦EMAT数学原理与有限元仿真
2.1 线聚焦EMAT数学原理
EMAT在试块内部激发超声波是多物理场耦合问题,既包含电磁场耦合又包含弹性波场,先通过电磁场计算得到试块趋肤层产生的洛伦兹力,再将洛伦兹力代入到弹性波场计算中就可以求解试块内部的超声位移场。因此,假设金属试样各向同性且满足线弹性假设和连续性假设,超声激发过程的控制方程可以表述为
fL=Je×B
(3)

2.2 线聚焦EMAT有限元建模
利用COMSOL Multiphysics 5.3a软件,建立有限元模型。如图2所示,整个模型分为4个部分:永磁体、铜导线曲折线圈、铝合金和空气域,其中永磁体位于曲折线圈正上方,铝板位于曲折线圈正下方,空气域包围整个EMAT结构。永磁体为方形磁铁,剩余磁通密度为1.2 T,矫顽力为899 kA/m,最大磁能积为297 kJ/m3,尺寸为50 mm×10 mm(l2×h2),提离距离t为1 mm。铝合金材料密度为2 700 kg/m3,杨氏模量为70 GPa,泊松比为0.33,电导率为37.7 MS/m,尺寸为100 mm×60 mm。导线添加材料为铜,其电导率为59.98 MS/m,线圈提离距离d为0.1 mm,模型所使用的相对磁导率和相对介电常数均为1。
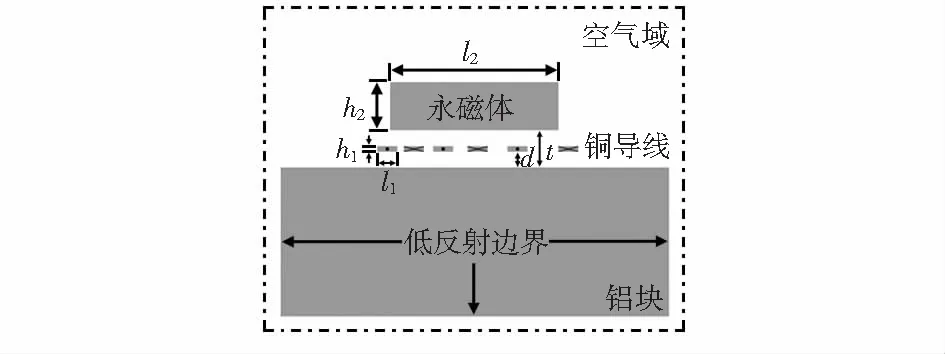
图2 线聚焦EMAT二维有限元物理模型
为了分析关键参数对换能器线聚焦性能的影响,本文选定2 MHz的电流激励频率f和50 mm的聚焦深度hF进行研究。模型的加载电流为正弦交流脉冲串,电流大小为30 A,激励周期N为6。模型中的线圈设计参数分别是:线圈匝数n为12匝,聚焦距离lF为10 mm,导线宽度l1为0.2 mm,导线厚度h1为0.035 mm,超声波在铝合金中传播速度c为3 100 m/s,因此,铜导线的位置关系可由式(1)、式(2)求出。
在进行网格划分时,为了得到更精确的解,模型中的铝块区域采用映射网格,并且保证一个波长范围内至少有10个网格单元,考虑到能量交换主要集中在铝合金表层,因此使用边界层网格对该区域进行网格细化,使一个趋肤深度内网格细分为5层。铝合金上表面设置为自由边界,其他3个表面设置为低反射边界以模拟无限大的铝板,避免反射回波对声场分布产生影响。
2.3 声场仿真结果分析
图3为不同时刻的超声波传播位移云图,所激发的超声波为SV波,从图中可以看出,在铝板表层形成的超声波沿着一个倾斜的角度在铝板内部传播,最后形成聚焦。

图3 不同时刻下超声波传播位移云图
为了便于定量地分析所激发的线聚焦SV波的声场分布情况,在模型的铝块内部取一条截线进行研究,截线通过设计焦点位置且平行于试块上表面,在水平方向上贯穿整个铝块宽度。提取截线上各点的面内位移幅值峰值,得到如图4(a)所示的水平方向上的声场分布曲线。
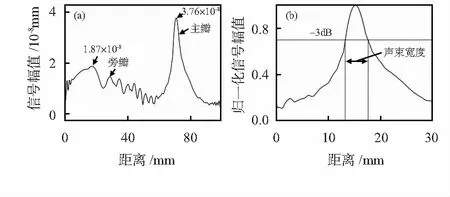
图4 线聚焦SV波在聚焦位置水平方向上的声场分布
如图4(a)所示,电磁超声线聚焦换能器除了在试块内部聚焦侧激发出声束主瓣外,也会在非聚焦侧激发出声束旁瓣。在模型的初始参数下,所激发的线聚焦SV波主瓣峰值达到3.76×10-8mm,最大旁瓣峰值为1.87×10-8mm,主瓣峰值是旁瓣峰值的2倍以上,由此可见,电磁超声线聚焦换能器所激发出的超声场具有明显的声场指向性。
在进行缺陷无损评估时,利用换能器激发出的声束主瓣进行检测,为了获得更好的缺陷检测效果,要求在设计的聚焦位置得到更高的主瓣峰值和更窄的声束宽度。因此,为便于对线聚焦SV波的声束宽度进行分析,以设计聚焦位置为中心,获取其在水平方向上30 mm范围内的声场分布曲线,其归一化结果如图4(b)所示,将线聚焦SV波声束宽度w(简称声束宽度)定义为最大信号幅值衰减-3 dB时对应的主瓣声束宽度,声束宽度越小,线聚焦能量越集中,声波对缺陷的空间分辨率越高,换能器的线聚焦性能越好。
3 关键参数对换能器线聚焦性能的影响分析
3.1 激励周期对线聚焦性能的影响
选取激励周期为3~8之间的6组数据,通过有限元计算后,按照2.3节的方法提取不同激励周期下的线聚焦主瓣峰值和声束宽度,分别以激励周期为横坐标,主瓣峰值和声束宽度为纵坐标,得到如图5所示的主瓣峰值和声束宽度与激励周期的关系曲线。由图5(a)可以看出,激励周期对主瓣峰值有显著影响,随着激励周期的增加,主瓣峰值先不断增大后趋于稳定,当激励周期由3增加到6时,主瓣峰值由1.91×10-8mm增加到3.76×10-8mm,提升至原来的1.97倍,信号强度提升效果明显;当激励周期再由6增加到8时,信号强度增强趋势减缓趋于稳定。由图5(b)可以看出,随着激励周期由3增加到6时,声束宽度由13.72 mm减小到4.36 mm,减小了68.2 %,声束宽度显著减小;当激励周期再由6增加到8时,声束宽度几乎不再减小而趋于稳定。因此,在一定范围内,适当增加信号激励周期既可以提高主瓣峰值,还可以减小声束宽度使聚焦能量更集中;但超过此范围,主瓣峰值和声束宽度均保持稳定,提升效果不明显。
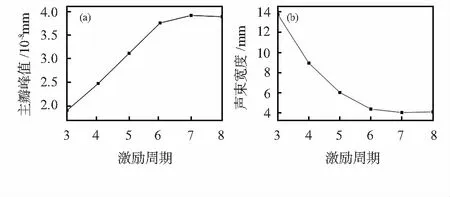
图5 主瓣峰值和声束宽度与激励周期的关系曲线
3.2 聚焦距离对线聚焦性能的影响
选取聚焦距离为2~22 mm之间的6组数据,通过有限元计算后,按照2.3节的方法提取不同聚焦距离下的线聚焦主瓣峰值和声束宽度,得到如图6所示的主瓣峰值和声束宽度与聚焦距离的关系曲线。由图6(a)可以看出,随着聚焦距离的增加,主瓣峰值以接近线性递减的趋势不断减小,当聚焦距离由2 mm增加到22 mm时,主瓣峰值由4.16×10-8mm减小到3.26×10-8mm,减小了21.6 %,信号强度明显减小。由图6(b)可以看出,随着聚焦距离的增大,声束宽度显著增大,当聚焦距离由2 mm增加到22 mm时,声束宽度由3.31 mm增大到8.28 mm,增大至原来的2.5倍,聚焦距离过大不利于线聚焦能量的集中,线聚焦性能变差。因此,聚焦距离的合理设计对提升电磁超声线聚焦换能器的声场聚焦效果至关重要,减小聚焦距离既可以获得更大的主瓣峰值,还可以减小声束宽度使聚焦能量更集中,获得更好的线聚焦性能。
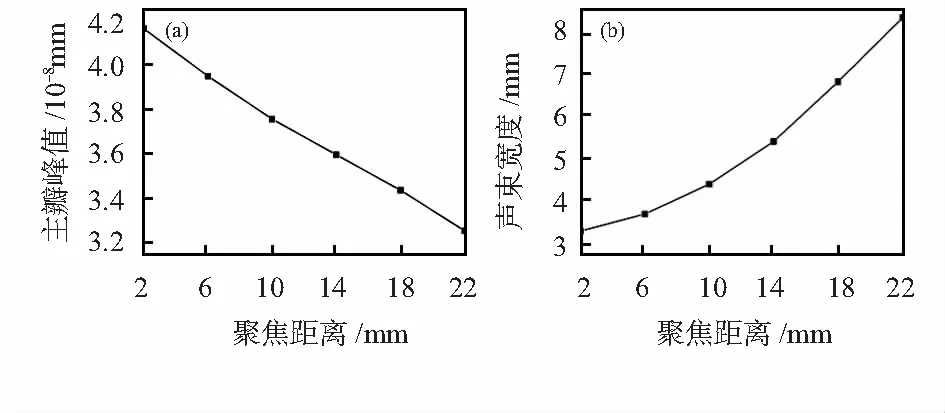
图6 主瓣峰值和声束宽度与聚焦距离的关系曲线
3.3 线圈匝数对线聚焦性能的影响
选取线圈匝数为6~16之间的6组数据,通过有限元计算后,按照2.3节的方法提取不同线圈匝数下的线聚焦主瓣峰值和声束宽度,得到如图7所示的主瓣峰值和声束宽度与线圈匝数的关系曲线。由图7(a)可以看出,随着线圈匝数从6匝增加到12匝时,主瓣峰值迅速增大,由2.02×10-8mm增大到3.76×10-8mm,提高为原来的1.86倍,信号强度明显增强,然而,当线圈匝数大于12匝时,随着线圈匝数进一步增加,主瓣峰值基本趋于稳定甚至表现出微弱的减小趋势;由图7(b)可以看出,随着线圈匝数的增多,声束宽度先变窄后变宽,当线圈匝数为10匝时,得到最小声束宽度为4.34 mm,此时线聚焦能量最集中,这种现象说明电磁超声线聚焦换能器的线圈匝数的选取存在一个极值点,对应着最小的声束宽度。因此,为了获得较高的主瓣峰值和更集中的线聚焦能量,应选取适当的线圈匝数,匝数过多和过少均不利于提高其线聚焦性能。
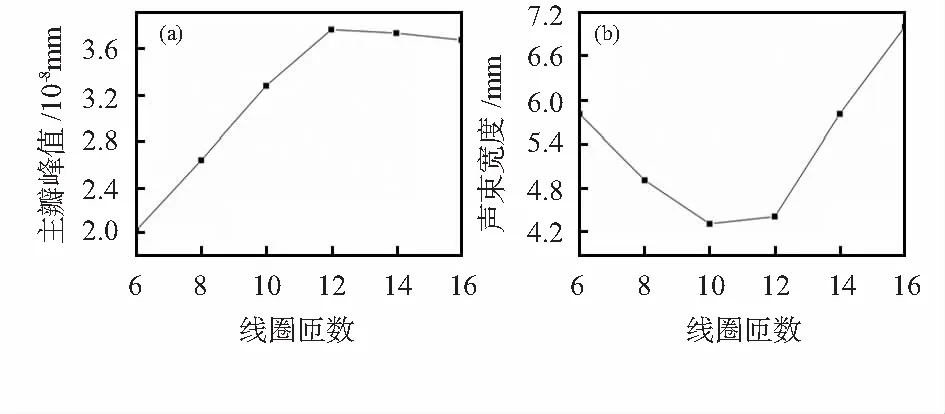
图7 主瓣峰值和声束宽度与线圈匝数的关系曲线
4 结 论
本文建立了电磁超声线聚焦换能器激发过程有限元模型,对换能器所激发的线聚焦SV波的声场分布情况进行了分析,通过提取表征换能器线聚焦性能的两个指标:主瓣峰值和声束宽度,研究了激励周期、聚焦距离和线圈匝数对线聚焦性能的影响。仿真结果表明:电磁超声线聚焦换能器所激发的超声场具有明显的指向性;适当增加激励周期、减小聚焦距离有利于提高线聚焦主瓣峰值并减小线聚焦声束宽度,使换能器的线聚焦能量更集中,获得更好的线聚焦效果;在进行换能器设计时应该选择适当的线圈匝数,匝数过多和过少均会使得线聚焦主瓣峰值降低和声束聚焦能量的分散,导致换能器线聚焦性能下降。
