不确定条件下考虑水循环过程的灌区多水源高效配置
2021-11-24曹凯华常雨晴
李 茉,曹凯华,付 强,刘 巍,胡 颜,常雨晴
不确定条件下考虑水循环过程的灌区多水源高效配置
李 茉,曹凯华,付 强※,刘 巍,胡 颜,常雨晴
(东北农业大学水利与土木工程学院,哈尔滨 150030)
灌区多水源配置涉及“大气水-地表水-土壤水-地下水”水循环过程,水文要素的变化增加了灌区多水源配置的复杂性,如何在不确定性条件下考虑农田水循环过程,将有限的不同来源的水量高效的分配到作物不同生育阶段,对促进灌区精准灌溉具有重要意义。基于此,该研究在径流与降水联合不确定性条件下,建立基于水循环过程的灌区多水源高效配置多目标模型,该模型耦合了Jensen模型与水短缺足迹模型,以实现节水增效的目的,并获得灌区高效配水方案对径流-降水联合不确定性的响应特征。结果表明:在不同径流与降水的组合情景下,基于各情景配水方案及发生概率,灌区主要生育期的综合配水量为2 241万m3,地表水与地下水的分配比例为6.5∶1,田间实际配水量占灌区可分配水量的95%;经济效益与田间配水量呈正相关关系,而水短缺足迹与田间配水量呈负相关,所构建的模型权衡了灌区经济效益、产量、蓝水利用量多个相互矛盾目标,与实际情况相比,灌区水分生产力可提高11%;不同情景下各生育阶段需要灌溉的程度不同,拔节期对缺水的敏感性最强,且水量分配变幅较大;分蘖期、拔节期和乳熟期采用以地表水灌溉为主,而抽穗期采用以地下水灌溉为主的方式可促进灌区节水增效;多水源配置方案使灌区灌溉的有效性在各情景下均呈现良好状态,可靠性在良好和中等水平之间,而灌区在灌溉的充分性方面有很大提升潜力。构建的模型能够反映水文要素的动态变化对灌区多水源配置的影响,明晰渠首引水与田间多水源配水的相互关系,并提出效益与用水效率同步提升的多水源配置方案,为灌区农业水资源的高效利用提供决策支持。
农田;水资源;水循环;高效配置;灌区;多水源;随机不确定性
0 引 言
中国农业发展很大程度上依赖于灌溉,灌区作为农业灌溉的主体,是农业生产的重要基地,对保障国家粮食安全和社会稳定具有重要作用[1]。灌区水资源配置是灌区管理的重要组成部分,也是区域或流域水资源配置的重要方面[2]。人口的增长和经济的快速发展导致灌区水资源短缺问题日益突出,在水资源短缺的背景下,不合理的使用与配置灌溉水资源将加剧水资源的供需矛盾。合理的优化配置灌区水资源,对提高灌区水资源利用效率及保障粮食安全、实现灌区水资源可持续利用具有重要意义。
灌区水资源短缺使灌区多水源联合配置成为研究热点,多种井渠结合的灌区多水源优化调度模型被建立及应用[3-8],为灌区多水源联合配置提供了模型构建方法与思路。研究表明,灌区多水源联合配置可有效提高灌区经济效益。例如,齐学斌等[3]根据水资源平衡原理,对山西省典型灌区的地表水和地下水进行联合优化调度。结果表明,通过采取水资源优化技术,在实现水资源采补平衡条件下,年经济效益可增加3 000元/hm2。Guo等[9]构建了一个基于AquaCrop模型的灌区作物灌溉制度优化模型框架,通过调整作物不同生育阶段的灌溉水量和灌水日期,可使灌溉经济效益较现状增长1.1%~9.7%。水资源供需矛盾的突出使高效节水灌溉的理念受到广泛关注。由此,在灌区多水源联合配置模型中,配置目标不应仅仅停留在追求经济效益最大上,灌区水资源利用效率应同样受到重视,尤其对于缺水严重的灌区而言。灌区配水效益、水资源利用效率的同步提升往往相互矛盾,为了解决该矛盾,近年来,多目标规划方法被应用于模型构建中,以实现灌区多水源的高效配置[10-12]。然而,基于多目标规划的灌区多水源高效配置是个复杂系统,仍存在一些问题需要解决。首先,灌区中作物生长依赖于土壤水、垂向的大气降水和水平向的灌溉水(来源于渠道输水和/或水井提水)进入土壤补充土壤水分供作物根系吸收,部分水分蒸发,部分水分下渗到地下含水层中,进而影响地下水取水量,灌区多水源联合配置涉及“四水”(大气水-地表水-土壤水-地下水)转化过程。现有的研究多数仅考虑灌区尺度供水条件,往往忽略了多水源联合配置中涉及到的农田水转化动态过程。其次,灌区多水源高效配置中通常通过经济效益最大、产量最大、配水量最小、渠道渗漏损失最小等几类目标来权衡灌区经济效益与用水量之间的矛盾,进而提高配水效率。这些目标函数在现有研究中通常采用线性规划来反映作物在整个生育期内所获得的最终效益与总配水,却忽略了各个生育阶段对整体效益及用水的累积作用及动态用水胁迫的影响,如何在灌区水循环动态变化情况下实现效益与用水效率的同步提升更是鲜有报道。此外,灌区多水源配置涉及复杂的水循环过程,不可避免的存在不确定性[13-14],且不同要素不确定性间相互影响,如垂直方向上的降水补给和水平方向上的径流补给的流量变化将影响渠道供水及农田水循环过程,共同影响水资源配置结果,考虑水文要素间的联合不确定性对灌区多水源高效配置的影响值得深入研究。
基于此,本文在考虑降水和供水联合不确定性条件下,构建基于水循环过程的灌区多水源联合配置多目标模型,以解决以下问题:1)在有限的可利用水量条件下动态地协调灌区效益与用水量之间的冲突,以实现灌区水资源的“高效”配置,其“高效”体现在用水效益和用水效率的同步提升;2)动态反映灌区供水、灌水、降水、耗水与需水之间的关系,有助于获得更加准确的多水源配置方案;3)获得灌区在降水和径流不同丰枯条件下的多水源配置方案,为降低由来水不确定性带来的灌区水资源配置风险提供参考。将构建的模型应用于水资源短缺的黑龙江省庆安县和平灌区的实例研究中,为灌区多水源高效配置提供决策方法,并提升灌区水资源利用应对变化环境的能力。
1 灌区多水源高效配置模型
1.1 模型构建
本节采用多目标规划方法来构建灌区多水源高效配置模型。模型目标函数为经济效益最大化和水短缺足迹最小化,通过决策灌区不同水源在作物不同生育阶段的配水量来权衡两个目标间的矛盾,进而达到节水增效的目的。两个目标受地表水可利用水量、水量平衡、地下水可开采量、配水量阈值、灌溉保证率、输水、补水等约束条件的限制,模型具体表达形式如下。
1.1.1 目标函数
1)经济效益最大化
灌区的经济效益一直都是农民和灌区管理者关注的重点,灌区的灌溉经济效益取决于作物产量。水分生产函数是描述作物产量与水之间的数学关系。本文引入适用性较强的Jensen连乘模型来表达不同生育阶段水分状况对作物最终产量形成的动态影响[15-16]。经济效益最大化目标函数可表示为
Jensen模型中的实际蒸散发量采用水量平衡方法来表示。降水、蒸发、径流、下渗、排水等水文过程导致作物实际蒸散发量发生相应的变化。针对水田(本文研究作物为水稻),其农田水循环过程简化为图 1所示(标有模型主要参数),本文未考虑潜水蒸发。
根据农田垂向方向上的水量平衡方程,Jensen模型中ETa()可表示为
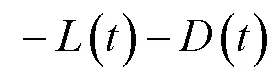
式中Δ()表示第-1与生育阶段田间水层深度差,()表示第生育阶段内降水量;()为渗漏量;()为排水量;式(2)中各变量单位均为m3/hm2。
2)水短缺足迹最小目标
在水资源短缺的大背景下,在保证灌区经济效益的同时,需控制用水总量,提高灌水效率。为了更好地衡量水资源的利用状况,Hoekstra等[17]在基于虚拟水的研究中提出了水足迹的概念。粮食水足迹可用于分析生产与消费过程中粮食生产对水资源消耗的响应,包括蓝水、绿水和灰水足迹。其中粮食蓝水足迹可理解为粮食生产对传统地表水和地下水资源的使用量,即农田灌溉用水量[18]。为了提高多水源的利用效率,应尽可能降低蓝水足迹。然而,作物水足迹却不能够反映灌溉用水的匮乏程度。为此,本文在作物蓝水足迹模型中引入水资源匮乏指数[19-20],构成水短缺足迹模型,并将其作为目标函数之一耦合到灌区多水源高效配置优化模型中,以同时表示粮食生产对水分利用的响应及水分胁迫,起到节约用水并提高灌溉水生产力的目的,该目标函数可表示为
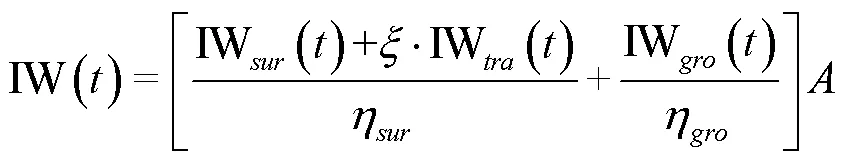
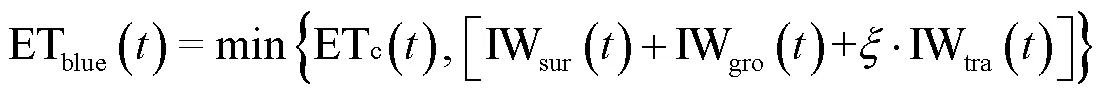
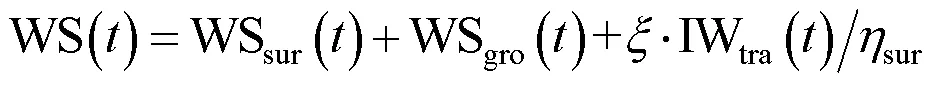
1.1.2 约束条件
上述两个目标函数受到如下条件约束:模型中的地表田间净灌溉水量(IWsur())与地下田间净灌溉水量(IWgro())为决策变量,它们通过农田水量平衡方程联系(式(2)),其中IWsur()由灌区可利用的引水量决定(约束1中的),IWgro()由灌区地下水可开采量决定(约束3中的)。设和相互独立,进而消除地表水、地下水之间的联系。各约束条件的数学表达式如下:
1)地表水可利用水量约束:由于灌区河流水资源量有限,不同生育阶段的地表水田间配水量(IWsur())不应超过该生育阶段的地表水可分配水量(WSsur())与上一阶段的地表水的剩余水量(RSsur(-1))之和。并且,由于灌区地表水主要来源于河流,因此灌区地表水的可分配量不应超过可从河流中引用的水量(),该约束条件表示如下:
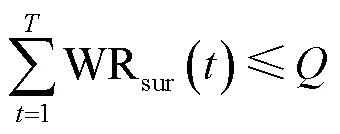
式中RSsur(-1)为上一阶段的剩余地表水量,m3,当=1,RSsur=0;为从河流中引水的可利用量,m3。
2)灌区水量平衡约束:作物各生育时期的剩余水量等于该阶段灌区地表水可分配量与上一生育阶段剩余水量之和减去此阶段的田间配水毛量。该约束可以表示为
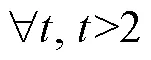
式中RSsur(-2)表示(-2)阶段所得剩余水量,m3;IWsur(-1)表示(-1)生育阶段的地表供水量,m3。
3)地下水可开采量约束:与地表水可利用量约束类似,不同生育阶段地下水田间配水量(IWgro())不应超过该生育阶段()地下水可分配量(WSgro())与上一生育阶段(-1)的深层渗漏量之和,并且地下水的可分配量不应超过地下水可开采量,该约束表示为
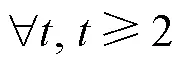
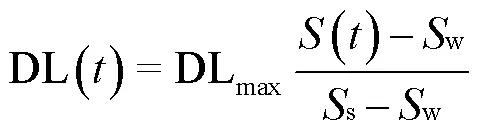
式中DL(-1)表示(-1)阶段的渗漏量,mm;DLmax为最大深层渗漏速率,mm/d;为单位换算系数;T()为第生育阶段天数,d;为地下水可开采量,m3;()为阶段的土壤含水量,mm;s为土壤饱和含水量,mm;w为土壤凋萎点对应的含水量,mm。
4)配水量阈值约束:作物不同生育阶段所有水源的田间配水量不应超过田间最大配水量,以避免水资源浪费,该约束可表示为
式中IAmax为田间最大配水量,m3/hm2。
5)灌溉保证率约束:所有水源的田间配水量应保证一定概率条件下需要灌溉的水量,以保证作物的生长与生产,该约束可表示为
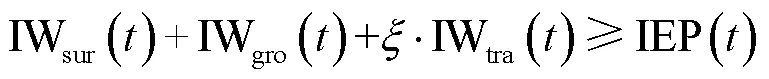
式中IEP()为某一灌溉保证率下的灌溉水量,m3/hm2。
6)输水约束:从渠首引水后在渠道中输送的水量要控制在渠道允许的最大和最小流量范围之内,保证渠道不淤不冲。该约束条件可表示为
式中QR()为输水渠道的安全运营流量值,m3/s;QRmin、QRmax分别为渠道安全运营的最小和最大流量,m3/s。
7)排水约束:当田面水深大于最大蓄水层深度时,需要排水,该约束条件[21]可表示为
式中()为地表蓄水层深度,m3/hm2;()为地表蓄水层最大深度,m3/hm2。
8)补水约束:若某一生育阶段地表水及地下水总量不能满足作物在某一灌水保证率下的最小灌溉水量,需要从水库调水。并且,由水库补充的水量不应超过水库在该生育阶段的可调水量,该约束可表示为
式中RES()为第生育阶段水库可调用的水量,m3/hm2。
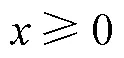
9)非负约束:所有的决策变量,包括作物不同生育阶段不同水源的田间配水量、灌区可分配水量、余水量,地表蓄水层深度等均不应为负值,该约束为
IWsur(),IWgro(),IWtra(),(),WSsur(),
WSgro(),RSsur() ≥0 (18)
1.2 水文要素联合不确定性
本文所构建的模型中,垂向的降水补给和水平向的地表水补给是两个重要的随机水文参数,直接影响灌区水资源配置结果[22]。地表水补给来源径流,径流与降水的年际年内变化显著。不同流量水平下的降水和径流共同影响农田水循环中各参数的变化,进而改变多水源配置方案。为了获得更加准确的水资源配置方案,更深入了解在极端情况下水资源利用及面临的经济风险,有必要获悉不同降水和径流丰枯组合情景下的灌区多水源配置方案的变化及相应方案发生的可能性大小。
式中为待定参数。常见的copula函数有高斯copula函数、t-copula、Gumbel copula、Frank copula和Clayton copula等。每种Copula函数对应其各自的结构函数和参数估计方法。关于采用Copula函数确定多个随机变量的发生概率的具体方法可参照文献[24-27]。
由于不同流量水平下的降雨量和径流量的实际水文序列较短,本文采用随机模拟方法将各要素不同流量的水文序列进行优化,进而优化Copula联合分布函数的边缘分布。根据随机模拟结果的均值确定各流量水平的代表值。设径流量与降水量均服从P-Ⅲ分布,采用舍选法对其进行随机模拟[28],其随机模拟公式为
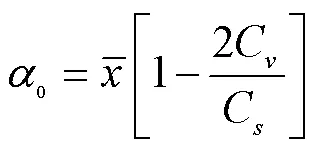
1.3 模型求解方法
本文构建的优化模型的性质为多目标非线性规划问题,问题可描述为
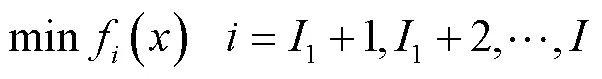
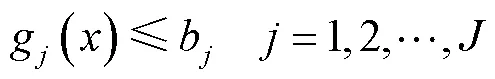
式中f()是第个目标函数,为目标函数的标量总个数;g()是第个约束,为约束标量的总个数;是决策变量,f() 和g()中至少有一个是非线性的。
国内外学者对于多目标模型解法的研究已较为深入,积累了大量成果。主要求解方法包括权重法、理想点法、约束法、神经网络、灰色系统、模糊理论、混沌理论、遗传算法以及各种方法组合等[29-31]。其中,Zimmerman法具有计算简单、可操作性强的优点,在多目标规划中得到了广泛的应用[32]。基于此,本文采用Zimmerman法将多目标规划模型转化为单目标模型。由于构建的模型具有非线性性质,因此模型在转化过程中采用非线性的隶属度函数。
对于最大化目标函数,其隶属度函数可表示为
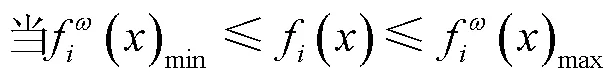
当f()<f()min时,[f()]=0,当f()>f()max时,[f()]=1。
对于最小化目标函数,其隶属度函数可表示为
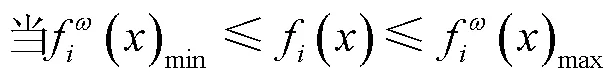
当f()<f()min时,[f()]=1,当f()>f()max时,[f()]=0。
式中[f()]表示非线性隶属度函数,f()表示第个目标函数;f()max和f()min分别是f()的最优值和最劣值;是一个辅助参数,对于非线性隶属度函数,>1。
利用“max-min”算子并引入满意度参数,将多目标非线性规划问题转换为单目标非线性问题求解,转化后的模型结构可表示为
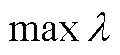

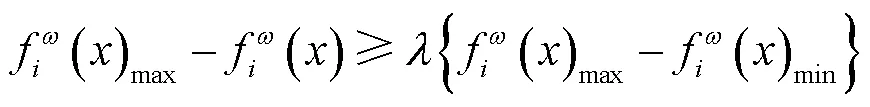
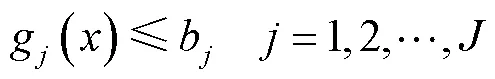
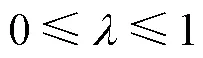
综上,考虑降水和径流的联合不确定性,本文所构建的灌区多水源高效配置模型的求解步骤如下:
1)构建灌区多水源高效配置优化模型;
2)确定灌区降水量和径流量等级划分标准,获得降水和径流在不同流量水平下的系列数据,对其进行随机模拟,根据随机模拟结果的均值确定降水和径流不同丰枯组合条件下(不同情景)的数值,作为优化模型的输入参数;
3)确定Copula函数边缘分布函数,拟合不同copula函数并检验,选定copula函数类型,并据此确定降水和径流的丰枯组合概率;
4)根据灌区实际情况,计算并确定灌区多水源高效配置优化模型的输入参数;
5)将各情景下的降水和径流量代入优化模型,求解单一目标模型,确定在各情景下的各目标函数的最大值和最小值;
6)构建各函数的非线性隶属度函数,将多目标非线性规划模型转换成单一目标非线性规划模型;
7)求解转化后的模型,寻求各情景下的水资源最优配置方案及相应目标函数值;
8)根据各情景的发生概率,确定综合配水方案及相应目标。
2 案例分析
2.1 灌区概况
本文选取位于国内最大商品粮生产基地松嫩平原的和平灌区为研究对象来验证构建模型的可行性。和平灌区是黑龙江省庆安县最大的灌区(125°55′~128°43′E,45°52′~48°03′N),隶属于呼兰河灌区,属温带半干旱半湿润大陆性季风气候。和平灌区年均降水量约545 mm,年均蒸发量约665 mm。河水和地下水是和平灌区灌溉的主要水源,此外,有柳河水库作为补充水源来缓解用水高峰期的缺水问题。和平灌区的地表水源为呼兰河、安邦河和拉林清河。灌区现有干渠一条,实际输水能力9 m3/s。灌区95%以上的耕地用于种植水稻,种植面积为0.729万hm2。“节水增产”是黑龙江省农业发展的目标,基于此,对和平灌区多水源高效配置是十分必要的。本文研究对象为和平灌区水稻田,在降水-径流组合情景下将不同来源的水分配到水稻不同生育时期(主要包括分蘖期、拔节期、抽穗期和乳熟期)。
2.2 情景设置
本文的情景为径流和降水不同丰枯流量组合模式。设灌区径流量和降水量都具有高流量、中流量和低流量三种水文特征。采用频率百分比将水文事件的水文特征分为低、中、高3级流量,划分的累积概率分别为P=75%,P=25%,即高流量>x,中流量x≤≤x,低流量<x,x为高、中流量分界值,x为中、低流量的分界值。假设表示年径流量值,表示年降水量值,、、分别为流量的高、中、低水平,、分别代表径流和降水的概率,则径流量和降水量之间的丰枯遭遇情景可分为以下9种类型:1)WH-PH(径流高流量-降水高流量),概率为(≥x,≥y);2)WH-PM(径流高流量-降水中流量),概率为(≥x,y<<y);3)WH-PL(径流高流量-降水低流量),概率为(≥x,<y);4)WM-PH(径流中流量-降水高流量),概率为(x<<x,≥y);5)WM-PM(径流中流量-降水中流量),概率为(x<<x,y<<y);6)WM-PL(径流中流量-降水低流量),概率为(x<<x,<y);7)WL-PH(径流低流量-降水高流量),概率为(<x,≥y);8)WL-PM(径流低流量-降水中流量),概率为(<x,y<<y);9)WL-PL(径流低流量-降水低流量),概率为(<x,<y)。
2.3 模型参数
本文涉及的数据主要包括气象数据、水文数据、灌区相关数据以及社会经济数据,相关数据来源于国家气象网(1956—2016)、黑龙江省统计年鉴(2000—2018)、黑龙江省水资源公报(2000—2018)、田间试验(2014 —2017)、灌区相关报告及相关参考文献。其中气象数据包括降水、气温(最大、最小、平均气温)、相对湿度、平均风速、日照时数等,除降水外的其他气象因子用于计算参考作物蒸散发量ET0(ET0,daily)用世界粮农组织FAO推荐的Penman-Monteith公式[33]计算得到。
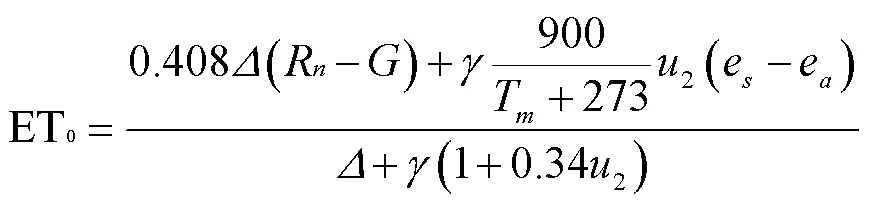
式中为饱和水汽压曲线的斜率,kPa/℃;R为净辐射量,MJ/(m2·d);为土壤热通量,MJ/(m2·d);为湿度计常数,kPa/℃;T为2 m高度处的空气平均温度,℃;2为地面以上2 m高度处的风速,m/s;e为空气饱和水汽压,kPa;e为空气实际水汽压,kPa,e-e为饱和水气压差,kPa。
在ET0基础上,可根据作物系数法计算,获得第生育阶段的作物蒸散发量(ETc(),mm):
式中()为第生育阶段的作物需水系数,随作物生育阶段变化;K()为第生育阶段的水分胁迫常数,可由下式确定:
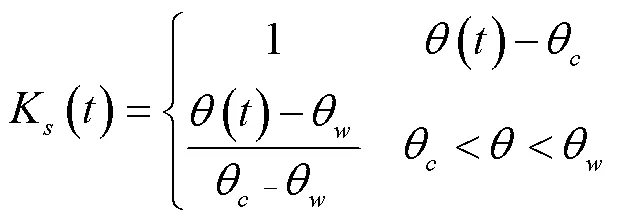
式中()为第生育阶段的土壤体积含水率,θ为凋萎系数,θ为临界含水率,是田间持水量(θ)与作物的土壤有效水分()的函数,可表示成θ=(1-)∙θ+∙θ,其中=θ- θ。
田间渗漏量可()由下式[34]获得。
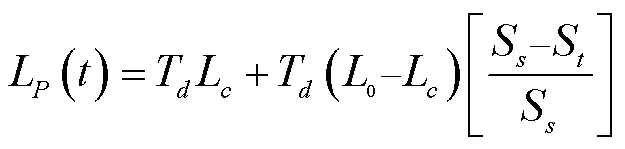
式中()为第生育阶段的地表潜在入渗量,mm;L()为浅层渗漏量,mm;S为饱和土壤体积含水量,mm;()为第生育阶段的田间土壤体积含水量,mm;0为初始下渗速率,mm/d;L为饱和下渗速率,mm/d。


表1 模型相关基础数据
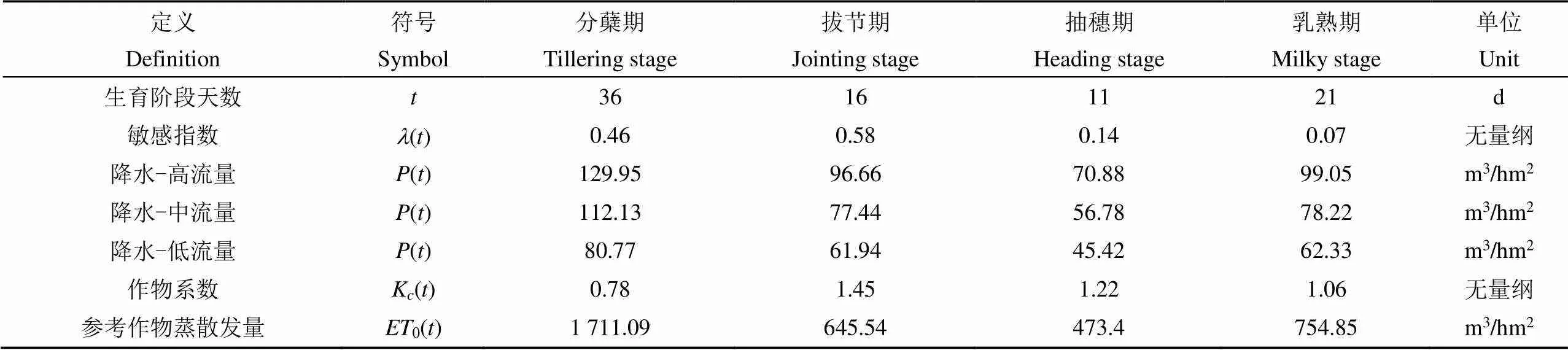
表2 作物不同生育阶段输入数据
2.4 灌溉效应评价
不同的灌溉配水方案直接影响灌区的水资源有效利用程度,而灌溉效应是水资源有效利用程度的最直接的数量化体现。本节通过灌溉的充分性(P)、有效性(P)和可靠性(P)三个方面来定量分析灌区灌溉效应[40],进而得到灌区水稻在不同生育阶段配水效率的差异,为灌区提高农业用水效率提供数据参考。
充分性可定义为系统满足需求的能力,可表示为
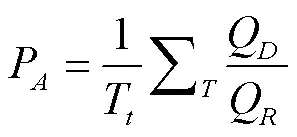
式中P为灌溉充分性指标;Q为实际用水量,104m3;Q为净需水量,104m3;T为时间,d。
有效性可定义为资源节约的能力,当一个系统提供了超过充足的供应时,它就不能被认为是有效的,灌溉有效性可表示为
式中P为灌溉有效性指标;Psingle为灌区以月为时间单位充分性指标。
可靠性可定义为在恰当的时间内供应水资源的能力,即不同生育阶段灌溉需水的供应能力,可表示为
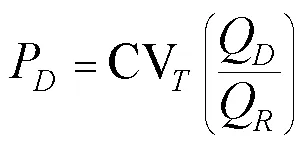
式中P为灌溉的可靠性指标;CV为在周期上的时间变异系数。
参考文献[41-42]建立的绩效指标评价标准,根据计算所获取的指标,将灌溉用水效应分为良好、一般和较差3个等级,如表3所示。

表3 灌溉效应评价表
注:P为灌溉充分性指标;P为灌溉的可靠性指标;P为灌溉有效性指标。下同。Note:P,P, andPareindexes used to assess sufficiency, reliability, and efficiency of irrigation, respectively. Same as below.
3 结果与分析
3.1 水资源总量配置
本文考虑了降水和径流的不同丰枯组合,并通过Copula函数确定其联合发生概率。采用较为常用的Gaussian copula、t-copula、Archimedean copula函数进行拟合,其中t-copula函数的拟合效果最好(平方欧式距离最小),因此采用t-copula作为联结函数,得到降水和径流丰枯组合联合发生概率,该联合发生概率有助于获得灌溉用水综合分配方案。综合配水量可通过不同情景的联合发生概率与对应配水量的加权求和获得。该综合配水方案有利于决策者掌握考虑不同情景下灌溉用水分配的总体情况。
模型经过优化求解后,得到和平灌区不同径流-降水情景下配水量图及综合配水结果(图2)。本文设定的各种情景中,径流和降水丰枯同步的发生概率为25.62%,丰枯异步的发生概率为74.38%。在不考虑调水的情况下,和平灌区综合配水量为2 241万m3,该综合配水量是降水和径流多种情景组合下的配水结果与相应发生概率的综合体现,考虑了不同情景配水方案发生的可能性,与配水均值比较更具有说服力。和平灌区的综合配水量小于多年平均可供水量2 929万m3。若不考虑补水,最不利的WL-PL情景下的灌区配水毛量为1 856万m3,在报告中和平灌区最小可供水量2 199万m3范围内。文献[5]通过构建区间多阶段随机规划模型对和平灌区的水资源进行分配,不同水文年的灌区总配水量在1 849~2 363万m3之间波动,本文获得的灌区综合配水量在这范围之内,但对作物不同生育阶段的配置结构进行了调整。这些表明本文获得的配置方案可行。总体看来,各情景中,地表水为主要供水水源,地表水与地下水的分配比例为6.5∶1。在地表径流量小且降水量少的情况下,需要从水库补水才能满足作物需水要求。例如,在WL-PM情景下,优化的地表、地下配水毛量分别为1 567万m3、327万m3,配水总量不能满足灌溉保证率要求,需水库补水174万m3。同样,在WL-PL情景下,优化的地表、地下配水毛量分别为1 531万m3、325万m3,需要至少补充336万m3水才能满足灌溉保证率要求。如图2显示,配水量对径流量和降水量的变化均较敏感,这也说明了在对作物进行水资源配置中考虑径流和降水联合不确定性的必要性。总体地,在降水量保持不变的情况下,配水量随着径流量的增加而增加;在径流量保持不变的情况下,配水量随降水量的增加而减少。该结论与Gong等[7,43]的研究成果变化趋势一致。
图3显示在不同情景下田间配水毛量、灌区可配水量和可利用水量之间的关系。其中田间配水毛量和灌区可配水量均为本文所构建模型的优化变量。田间配水毛量等于地表水田间配水量(IWsur(),模型优化获得)除以地表水利用系数与地下水田间配水量(IWgro(),模型优化获得)除以地下水利用系数在所有生育阶段的求和。灌区可配水量为模型直接优化获得的地表可分配水量(WSsur())与地下可分配水量(WSgro())在所有生育阶段的求和。可利用水量为地表可利用水量()与地下水可开采量()之和。上述各变量在各生育阶段中若需补水,则加上相应的补水毛量。如图所示,在任一情景下,田间配水毛量小于灌区可分配水量,而灌区可分配水量小于或者等于灌区可利用水量。最优田间配水毛量占最优灌区可分配水量的95%。和平灌区水资源短缺,优化的灌区可分配水量没有全部分配到田间,是由于模型是两个相互矛盾的目标函数的综合结果,同时也受渠道输水能力的限制。从图中不难发现,在径流水平低或降水水平低的情况下,如情景WL-PH、WL-PM、WL-PL、WH-PL、WM-PL,优化的灌区可分配水量接近可利用水量,而在径流水平高或降水水平高的情况下,优化灌区可分配水量小于可利用水量。该结果表明,在水资源短缺的情况下,模型的优化结果更倾向于充分利用有限的水资源来保证经济效益,而当水量较充足的情况下,水分利用效率的提高也被考虑。
3.2 不同生育阶段水量变化
地表水灌溉、地下水灌溉和降水是水稻在田间的主要补给水源。图4a和图4b为不同情景下地表水和地下水在不同生育阶段的变化情况。分蘖期的总水量分配最大,其次是拔节期,抽穗期与乳熟期的配水量相当。优化的结果由生育阶段天数、作物需水、降水、缺水敏感性、输水情况及配水目标共同决定的。不同的径流与降水水平会改变不同生育期不同水源的水量分配结构。分蘖期、拔节期、抽穗期、乳熟期的水量分配比例分别为(44.06%±1.54%)、(22.78%±1.55%)、(16.56%±1.26%)、(16.59%±3.99%)。其中分蘖期地表水、地下水与降水的分配比例约为0.65∶0.25∶0.11;拔节期地表水、地下水与降水的分配比例约为0.62∶0.13∶0.15;抽穗期地表水、地下水与降水的分配比例约为0.31∶0.54∶0.16;乳熟期地表水、地下水与降水的分配比例约为0.67∶0.12∶0.21。分蘖期、拔节期和乳熟期的地表水和地下水分配比例基本一致,而抽穗期中地下水的分配占主导地位。根据水量平衡方程,可得到各水稻在各生育阶段的耗水量,而耗水量与需水量的比值(相对耗水量)有助于了解各生育阶段的水分亏缺状况及对产量的贡献,如图4c所示,尽管分蘖期和拔节期的总田间配水量比抽穗期和乳熟期的多,但相对耗水量却明显偏低,尤其是拔节期,这与灌区的总水量供应不足直接相关。由于缺水,灌区的水稻需要非充分灌溉,为了同时满足灌区效益最大和水短缺足迹最小两个目标,拔节期成为缺水最敏感的阶段,若加大投入进行补水,应优先分配给拔节期。在所有生育期中,分蘖期和拔节期的水量分配和相对耗水变幅较大,这两个生育期虽是配水关键期,但在不同水量供给条件下,其水量分配的鲁棒性相对抽穗期与乳熟期较差,但波动程度比实际小。分蘖期、拔节期在多种情景下的最优配水量为(842±60)、(436±48)m3/hm2,且优化的最大、最小值均在报告中相应的最大、最小值范围之内。分蘖期、拔节期的水量优化分配结果均值与报告中55 a的灌溉制度表中的结果分别相差14%、18%,均不超过20%。优化的水稻田间净灌溉定额为1 913.84 m3/hm2,比实际降低17%,小于20%。若将水资源视为水文要素,将优化配置结果视为预报值,根据SL250—2000《水文情报预报规范》[44],可取预见期内实测变幅的20%作为允许误差,一次预报的误差小于许可误差时为合格预报。通过与实际比较,可判定模型的优化结果较准确。
3.3 目标权衡与灌溉效应分析
本文所构建的模型考虑了两个目标函数,即最大经济效益目标与最小水短缺足迹目标。从目标函数的数学表达式来看,最大经济效益目标倾向于分配更多的水量以获得更大的经济效益,但是基于水量分配的田间耗水不能大于需水,以免造成产量下降和水资源浪费的双亏现象。最小水短缺足迹目标函数的数学表达形式为分式非线性,整体来讲倾向于在满足作物灌水保证率前提下尽可能分配更少的水量以减少水分胁迫,其中蓝水足迹部分分子上数学表达的物理意义是分配到田间的水量,倾向于分配更少的水量以减少蓝水利用量,而分母上数学表达的物理意义是作物的产量,在需水控制下倾向于分配更多的水量以获得更高的产量。水短缺足迹目标本身就存在水量分配的权衡,加之与最大经济效益目标的权衡,所构建的灌区多水源分配多目标模型是水量分配在综合权衡多方面目标矛盾的结果。图5a显示经济效益与水短缺足迹的关系。总体而言,经济效益的降低与水短缺足迹的增加成正比。换言之,水短缺会导致经济效益降低,同时也会带来更大的水分胁迫。9种情景的经济效益在[2 302, 4 209]万元范围内波动,而水短缺足迹在[0.52, 0.57] m3/kg范围内波动。该水短缺足迹考虑了水匮乏指数,9种情景的平均水匮乏指数为0.92,属于极度水分胁迫状态,说明研究区域水资源短缺的现状。根据模型结果可以获得灌溉水生产力,即单位灌溉水量下的粮食产量。模型结果显示,并不是水量分配越多,灌溉水生产力越大,9种情景下灌区水稻的灌溉水利用效率在[1.59, 1.80] kg/m3(不考虑缺水胁迫)之间波动。考虑不同来水情况下的发生概率,模型的综合经济效益为3 269万元,比实际经济效益降低3.82%,但比实际节水19.98%,其中WL-PH情景下,节水效果最显著。灌区整体综合灌溉水生产力提高11%。
因为所构建模型的两个目标之间存在权衡,所以综合考虑两个目标的配水结构比单独考虑某个目标的配水结构有所调整。如前所述,经济效益目标倾向分配越多的水量而水短缺足迹目标倾向分配越少的水量,令单独考虑两个目标函数所优化的水量之间的距离为1,图5b显示在综合考虑这两个相互矛盾的目标情况下水量分配的权衡结果。如图中配水量距离两个目标配水量的距离所示,优化的结果权衡了两个目标,但是结果仍然倾向于在有限的可利用水量前提下分配更多的水量以获得更高的经济效益,尤其对于情景WH-PH、WM-PL和WL-PL而言。个别情景的优化配水结果倾向于水短缺足迹目标,如情景WH-PL。该结果也再次说明不同的来水情况对水资源配置影响显著。因此,讨论不同来水情况下水资源配置问题是有必要的。需要说明的是,所构建的模型中各个约束条件对于两个目标函数均有限制作用,但最敏感的约束条件为可利用水量约束和灌溉保证率约束,在一定的供水条件下,灌区设定灌溉保证率得不到满足时,则启用补水约束条件。
一般来说,P、P、P表示实际供水与作物需水量之间的关系,可以作为灌溉方案中性能的综合反映。通过式(38)~式(40)计算得到和平灌区灌溉效应评价结果,如表4所示。
结果显示(表4),和平灌区的灌溉充分性能均表现较差,表明该灌区实际灌溉量不能满足作物需水量,一定程度反映了该灌区灌溉充分性不足,供水不均衡,该项指标仍有很大的提升潜力。其中,WH-PL情景P值最大为0.59,而WL-PH情景充分性指标最小,仅为0.44。不同情景下灌溉系统的有效性均为1,在所有情景下的灌溉有效性均达到良好,表明灌区灌溉水量损失较小,节水能力较强。灌区的可靠性指标在0.06(WL-PL)~0.19(WL-PM)之间变化。WH-PH、WH-PM、WM-PM、WL-PM情景下的灌水可靠性为中等水平,其余情景灌水可靠性均表现良好。各情景灌溉有效性均呈现良好,可靠性在良好和中等之间波动,而充分性表现均较差,一定程度上表明灌区虽然缺水严重,但是供水可靠,用水效率高。综合目标权衡与灌溉效应分析,根据模型输出,以节水量、灌溉水利用效率、单位效益用水量、水短缺足迹、灌溉定额、灌水充分性、灌水有效性、灌水可靠性8个指标建立节水效果评估体系,采用均值-标准差分级法[45]对各指标进行分析,采用模糊综合评判法[46]对灌区节水效果进行评价,结合各情景发生概率,得到灌区综合节水效果为Ⅱ级(共Ⅴ级,级数越低,节水效果越显著),节水效果较好。
4 结 论
本文构建了灌区多水源高效配置多目标模型,将所构建的模型应用黑龙江省庆安县的和平灌区,得到径流和降水不同流量组合情景下的灌区多水源高效配置方案。结果表明:
1)在降水与地表供水不同流量水平下,和平灌区水稻田在分蘖→拔节→抽穗→乳熟生育期的单位面积灌溉水量在整个生育期的比例在(44.06%±1.54%)、(22.78%±1.55%)、(16.56%±1.26%)、(16.59%±3.99%)间波动,总综合配水量为2.241×107m3,该配水量综合了径流与降水在不同流量水平下的配置方案与方案发生的可能性,有利于决策者掌握灌区灌溉用水分配的总体情况。
2)模型协调经济效益最大目标和水短缺足迹最小两个相互矛盾的目标,与灌区实际情况进行对比,协调结果可使灌区在灌溉经济效益降低3.82%的代价下,节水19.98%,其中径流为低流量且降水为高流量水平下的节水效果最为显著,灌区整体水分生产力提高11%。
3)不同径流与降水流量组合情景下各生育阶段的多水源配比及配水趋势均发生改变,总体来讲,抽穗期地下水的分配占主导地位,其余生育期地表水占主导地位,拔节期为缺水最敏感阶段,其地表水、地下水与降水的分配比例约为0.62∶0.13∶0.15。
4)不同情景下灌区多水源灌溉的有效性呈现良好状态,可靠性在良好和中等水平之间波动,而灌区在灌溉的充分性方面仍有很大提升潜力。
本文构建的灌区多水源高效配置多目标模型的创新性及贡献体现在:1)在多水源联合配置优化模型中耦合了表征“大气水-地表水-土壤水-地下水”转化过程,有利于获得更加准确的地表水和地下水动态配置方案;2)动态反映了耗水、需水、用水与供水的相互关系对灌区效益与用水效率的累积影响,并同时协调了灌区效益与灌水效率之间的矛盾;3)综合考虑水平向径流补给与垂向降水补给对灌区多水源配置的联合影响,提供更真实的灌区多水源决策支持。所构建模型为高度非线性多目标规划模型,采用耦合非线性隶属度函数的Zimmerman法对模型进行求解,其中径流与降水的不确定性采用Copula函数与随机模拟相结合的方法进行量化与优化。
本文构建的灌区多水源高效配置模型的应用价值主要体现在其能促进灌区水资源的“高效-节水”管理,并提升灌区配水应对来水变化的能力。模型的结果可对和平灌区水资源管理提供实际指导。例如:当预测的径流量低于1 583万m3,且降水量低于325 mm时,需做好水库补水的准备,至少需要水库补充174万m3水才能满足水稻50%的灌溉保证率。若有补充水源,则应优先把补充水源的水分配到水稻的拔节期。在分蘖期、拔节期和乳熟期采用以地表水灌溉为主(地表水、地下水与降水的分配比例均值如下:分蘖期为0.65∶0.25∶0.11、拔节期为0.62∶0.13∶0.15、乳熟期为0.67∶0.12∶0.21),而抽穗期采用以地下水灌溉为主(地表水、地下水与降水的分配比例均值0.31∶0.54∶0.16)的方式更有利于灌区节水增效。构建的模型框架可应用于其他以水田为主的缺水型灌区,为灌区农业水资源的高效利用提供决策支持。
[1] 杜丽娟,陈根发,柳长顺,等. 基于GWAS模型的灌区水资源优化配置研究:以淠史杭灌区为例[J]. 水利水电技术,2020,51(12):26-35.
Du Lijuan, Chen Genfa, Liu Changshun, et al. GWAS model-based optimal allocation of water resources in irrigation district[J]. Water Resources and Hydropower Engineering, 2020, 51 (12): 26-35. (in Chinese with English abstract)
[2] 齐学斌,黄仲冬,乔冬梅,等. 灌区水资源合理配置研究进展[J]. 水科学进展,2015,26(2):287-295.
Qi Xuebin, Huang Zhongdong, Qiao Dongmei, et al. Research advances on the reasonable water resources allocation in irrigation district[J]. Advances in Water Science, 2015, 26(2): 287-295. (in Chinese with English abstract)
[3] 齐学斌,樊向阳,王景雷,等. 井渠结合灌区水资源高效利用调控模式[J]. 水利学报,2004,35(10):119-124.
Qi Xuebin, Fan Xiangyang, Wang Jinglei, et al. Optimal allocation of water resources in well-canal combined irrigated area for high efficient utilization of water[J]. Journal of Hydraulic Engineering, 2004, 35(10): 119-124. (in Chinese with English abstract)
[4] 岳卫峰,高鸿永,陈爱萍,等. 基于GAMS的内蒙古河套灌区水资源联合利用分析[J]. 南水北调与水利科技,2013,11(3):12-16.
Yue Weifeng, Gao Hongyong, Chen Aiping, et al. Study on conjunctive use of water resources in Hetao Irrigation District of Inner Mongolia based on GAMS simulation and optimization[J]. South-to-North Water Transfers and Water Science&Tech-nology, 2013, 11(3): 12-16. (in Chinese with English abstract)
[5] 付强,刘银凤,刘东,等. 基于区间多阶段随机规划模型的灌区多水源优化配置[J]. 农业工程学报,2016,32(1):132-139.
Fu Qiang, Liu Yinfeng, Liu Dong, et al. Optimal allocation of multi-water resources in irrigation area based on interval-parameter multi-stage stochastic programming model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(1): 132-139. (in Chinese with English abstract)
[6] Zeinali M, Azari A, Heidari M M. Multiobjective optimization for water resource management in low-flow areas based on a coupled surface water-groundwater model[J]. Journal of Water Resources Planning and Management, 2020, 146(5): 04020020.
[7] Gong X, Zhang H, Ren C, et al. Optimization allocation of irrigation water resources based on crop water requirement under considering effective precipitation and uncertainty[J]. Agricultural Water Management, 2020, 239: 106264.
[8] Zhang F, Guo P, Engel B A, et al. Planning seasonal irrigation water allocation based on an interval multiobjective multi-stage stochastic programming approach[J]. Agricultural Water Management, 2019, 223: 105692.
[9] Guo D, Olesen J E, Manevski K, et al. Optimizing irrigation schedule in a large agricultural region under different hydrologic scenarios[J]. Agricultural Water Management, 2021, 245: 106575.
[10] Wang Y Z, Liu L, Guo S S, et al. A bi-level multi-objective linear fractional programming for water consumption structure optimization based on water shortage risk[J]. Journal of Cleaner Production, 2019, 237: 117829.
[11] 潘琦,郭萍,张帆,等. 考虑渠道渗漏的黄羊灌区农业水资源多目标优化配置研究[J]. 水资源与水工程学报,2020,31(4):166-173.
Pan Qi, Guo Ping, Zhang Fan, et al. Study on multi-objective optimal allocation of agricultural water resources in Huangyang Irrigated Area considering canal leakage[J]. Journal of Water Resources and Water Engineering, 2020, 31(4): 166-173. (in Chinese with English abstract)
[12] 何英,唐晓宇,彭亮,等. 南疆丰收灌区水资源多目标优化配置方案优选[J]. 农业工程学报,2021,37(6):117-126.
He Ying, Tang Xiaoyu, Peng Liang, et al. Optimized selection of the solution for multi-objective optimal allocation of water resources in Fengshou Irrigation Areas of South Xinjiang[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(6): 117-126. (in Chinese with English abstract)
[13] 谭倩,缑天宇,张田媛,等. 基于鲁棒规划方法的农业水资源多目标优化配置模型[J]. 水利学报,2020,51(1):56-68.
Tan Qian, Gou Tianyu, Zhang Tianyuan, et al. A multi-objective robust programming model for agricultural water management with uncertain weights[J]. Journal of Hydraulic Engineering, 2020, 51(1): 56-68. (in Chinese with English abstract)
[14] Li M, Fu Q, Singh V P, et al. Managing agricultural water and land resources with tradeoff between economic, environmental, and social considerations: A multi-objective non-linear optimization model under uncertainty[J]. Agricultural Systems, 2020, 178: 102685.
[15] 丛振涛,周智伟,雷志栋. Jensen模型水分敏感指数的新定义及其解法[J]. 水科学进展,2002,13(6):730-735.
Cong Zhentao, Zhou Zhiwei, Lei Zhijie. New definition and computation on the water sensitive index in Jensen model[J]. Advances in Water Science, 2002, 13(6): 730-735. (in Chinese with English abstract)
[16] 李中恺,刘鹄,赵文智. 作物水分生产函数研究进展[J]. 中国生态农业学报,2018,26(12):1781-1794.
Li Zhongkai, Liu Hu, Zhao Wenzhi. Revisiting crop water production functions in terms of cross-regional applications[J]. Chinese Journal of Eco-Agriculture, 2018, 26(12): 1781-1794. (in Chinese with English abstract)
[17] Hoekstra A Y, Hung P Q. Virtual water trade: A quantification of virtual water flows between nations in relation to international crop trade[J]. Water Science & Technology, 2002, 49(11): 203-209.
[18] 李桐,董维红,张琦琛,等. 基于时间序列模型的黑龙江省粮食水足迹分析与预测[J]. 排灌机械工程学报,2020,38(11):1152-1159.
Li Tong, Dong Weihong, Zhang Qichen, et al. Analysis and prediction of grain water footprint in Heilongjiang province based on time series model[J]. Journal of Drainage and Irrigation Machinery Engineering, 2020, 38(11): 1152-1159. (in Chinese with English abstract)
[19] Gheewala S H, Silalertruksa T, Nilsalab P, et al. Water stress index and its implication for agricultural land-use policy in Thailand[J]. International Journal of Environmental Science and Technology, 2018, 15(4): 833-846.
[20] Li J W, Liu Z F, He C Y, et al. Water shortages raised a legitimate concern over the sustainable development of the drylands of northern China: Evidence from the water stress index[J]. Science of the Total Environment, 2017, 590/591: 739-750.
[21] 闫旖君,徐建新,陆建红. 人民胜利渠灌区多水源循环转化模型研究[J]. 灌溉排水学报,2017,36(2):52-57.
Yan Yijun, Xu Jianxin, Lu Jianhong. Research on the Multi-water Cycle and Transformation Model in the People’s Victory Canal Irrigation District[J]. Journal of Irrigation and Drainage, 2017, 36(2): 52-57. (in Chinese with English abstract)
[22] Yang G Q, Li M, Guo P. Monte Carlo-based agricultural water management under uncertainty: A case study of Shijin Irrigation District, China[J/OL]. Journal of Environmental Informatics, 2021. Doi: 10. 3808/jei. 202000441.
[23] 刘章君,郭生练,许新发,等. Coplula函数在水文水资源中的研究进展与述评[J]. 水科学进展,2021,32(1):148-159.
Liu Zhangjun, Guo Shenglian, Xu Xinfa, et al. Application of Copula functions in hydrology and water resources: A state-of-the-art review[J]. Advances in Water Science, 2021, 32(1): 148-159. (in Chinese with English abstract)
[24] Chen S, Xu J, Li Q, et al. A copula-based interval-bistochastic programming method for regional water allocation under uncertainty[J]. Agricultural Water Management, 2019, 217: 154-164.
[25] 周念清,赵露,沈新平. 基于Copula函数的洞庭湖流域水沙丰枯遭遇频率分析[J]. 地理科学,2014,34(2):242-248.
Zhou Nianqing, Zhao Lu, Shen Xinping. Copula-based probability evaluation of rich-poor runoff and sediment encounter in Dongting Lake Basin[J]. Scientia Geographica Sinica, 2014, 34(2): 242-248. (in Chinese with English abstract)
[26] 康玲,何小聪. 南水北调中线降水丰枯遭遇风险分析[J]. 水科学进展,2011,22(1):44-50.
Kang Ling, He Xiaocong. Risk analysis of synchronous-asynchronous encounter probability of rich-poor precipitation in the Middle Route of South-to-North Water[J]. Advances in Water Science, 2011, 22(1): 44-50. (in Chinese with English abstract)
[27] 吴宇彤,钟平安,万新宇,等. 基于copula函数的韩-榕-练三江径流丰枯遭遇分析[J]. 水力发电,2021,47(3):10-15,125.
Wu Yutong, Zhong Ping'an, Wan Xinyu, et al. Study on the wetness-dryness encountering of inflow of hanjiang-rongjiang-lianjiang rivers based on copula functions[J]. Water Power, 2021, 47(3): 10-15, 125. (in Chinese with English abstract)
[28] 顾文权,邵东国,黄显峰,等. 水资源优化配置多目标风险分析方法研究[J]. 水利学报,2008,39(3):339-345.
Gu Wenquan, Shao Dongguo, Huang Xianfeng, et al. Multi-objective risk assessment on water resources optimal deployment[J]. Journal of Hydraulic Engineering, 2008, 39(3): 339-345. (in Chinese with English abstract)
[29] Marler R T, Arora J S. Survey of multi-objective optimization methods for engineering[J]. Structural and Multidisciplinary Optimization, 2004, 26: 369-395.
[30] 刘建军,司光亚,王艳正,等. 基于模型的多目标优化问题方法研究[J]. 系统仿真学报,2020,32(11):2138-2145.
Liu Jianjun, Si Guangya, Wang Yanzhang, et al. Research on multi-objective optimization method based on model[J]. Journal of System Simulation, 2020, 32(11): 2138-2145. (in Chinese with English abstract)
[31] 崔慧敏. 基于多目标规划的城市水资源优化配置研究[D]. 西安:西安理工大学,2020.
Cun Huimin. Research on Optimal Allocation of Urban Water Resources Based on Multi-Objective Planning[D]. Xi'an: Xi'an University of Technology, 2020. (in Chinese with English abstract)
[32] Li M, Fu Q, Singh V P, et al. An intuitionistic fuzzy multi-objective non-linear programming model for sustainable irrigation water allocation under the combination of dry and wet conditions[J]. Journal of Hydrology, 2017, 555: 80-94.
[33] Allen R G, Pereira, L A, Raes D, et al. Crop evapotranspiration: Gudelines for computing crop water requirements-FAO Irrigation and Drainage Paper 56[R]. Rome: Food and Agricultural Organization of the United Nations (FAO), 1998: 56.
[34] Chien C P, Fang W T. Modeling irrigation return flow for the return flow reuse system in paddy fields[J]. Paddy & Water Environment, 2012, 10(3): 187-196.
[35] Li M, Guo P, Singh V P, et al. An uncertainty-based framework for agricultural water-land resources allocation and risk evaluation[J]. Agricultural Water Management, 2016, 177: 10-23.
[36] 陈苏燕,卫琦,徐俊增,等. 不同耗水强度下节水灌溉稻田土壤含水率与非饱和土层厚度关系研究[J]. 中国农学通报,2018,34(11):147-151.
Chen Suyan, Wei Qi, Xu Junzeng, et al. Water-saving irrigation paddy field: The relationship between soil moisture content and the thickness of unsaturated soil layer under different water consumption intensities[J]. Chinese Agricultural Science Bulletin, 2018, 34(11): 147-151. (in Chinese with English abstract)
[37] Liu W, Fu Q, Meng J, et al. Simulation and analysis of return flow at the field scale in the northern rice irrigation area of China[J]. Agricultural Water Management, 2019, 224: 105735.
[38] 于婧. 寒区水稻需水规律及水分胁迫影响研究[D]. 哈尔滨:东北农业大学,2013.
Yu Jing. Study of Water-demand Regulations and Water Stress of Rice in fold Regions[D]. Harbin: Northeast Agricultural University, 2013. (in Chinese with English abstract)
[39] 尹必文,曹明龙,唐淑菊. 水稻不同种植方式的优缺点及成本分析[J]. 现代农业科技,2020(12):52-53.
Yin Biwen, Cao Minglong, Kang Shuju. The advantages and disadvantages of different rice planting methods and cost analysis[J]. Modern Agricultural Science and Technology, 2020(12): 52-53. (in Chinese with English abstract)
[40] Unal H B, Asik S, Avic M, et al. Performance of water delivery system at tertiary canal level: A case study of the Menemen Left Bank Irrigation System, Gediz Basin, Turkey[J]. Agricultural Water Management, 2004, 65(3): 155-171.
[41] Fan Y, Gao Z, Wang S, et al. Evalulation of the water allocation and delivery performance of Jiamakou irrigation scheme, Shanxi, China[J]. Water, 2018, 10(5): 654.
[42] Elnmer A, Khadr M, Allam A, et al. Assessment of irrigation water performance in the Nile Delta using remotely sensed data[J]. Water, 2018, 10(10): 1357.
[43] Chen Y, Cai Y, Wang X, et al. An inexact modeling approach for supporting water resources allocation under natural and social complexities in a border city of China and Myanmar[J]. Resources, Conservation & Recycling, 2021, 168: 105245.
[44] 水文情报预报规范:SL 250-2000(条文说明) [S].
[45] 付强,姜秋香,焦立国,等. 黑龙江省半干旱区水土资源可持续利用研究[M]. 北京:中国水利水电出版社,2010,12.
[46] 汪顺生,刘东鑫,王康三,等. 不同沟灌方式对夏玉米耗水特性及产量影响的模糊综合评判[J]. 农业工程学报,2015,31(24):89-94.
Wang Shunsheng, Liu Dongxin, Wang Kangsan, et al. Fuzzy comprehensive evaluation on water consumption characteristics and yield of summer corn under different furrow irrigation patterns[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(24): 89-94. (in Chinese with English abstract)
Efficient allocation of multiple water sources in irrigation areas considering water cycle process under uncertainty
Li Mo, Cao Kaihua, Fu Qiang※, Liu Wei, Hu Yan, Chang Yuqing
(,150030,)
Precise configuration of multiple water sources in irrigation areas is closely involved with the whole water cycle process of “atmospheric water-surface water-soil water-groundwater”. Particularly, changes in hydrological elements can pose a great complexity on the multi-source configuration of irrigation areas. It is very necessary to consider the water cycle process under uncertainty, thereby efficiently allocating the limit water availability to different growth stages of crops in precision irrigation. In this study, a multi-objective model was established to optimize the efficient allocation of multiple water sources under the combined uncertainty of runoff and precipitation in an irrigation area using the water cycle process. Jensen and water scarcity footprint models were also coupled to achieve the synchronization of economic benefits and water saving. An attempt was made to obtain the response characteristics of efficient water distribution to the combined uncertainty of runoff and precipitation. The results showed that the comprehensive water allocation during the main growth period in the irrigation area was 22.41 million m3under different combined scenarios of surface water supply and precipitation using the water allocation plan and occurrence probability of each scenario. Specifically, the proportion of surface water and groundwater was 6.5∶1, while the water allocation in the field accounted for 95% of the optimal water availability. Furthermore, the goal of economic benefit presented a positive correlation with the field water allocation amount, while the goal of water scarcity footprint presented a negative correlation. The constructed model was also used to weigh the conflict goals of economic benefit, yield and blue water use. In addition, the water productivity increased by 11% in the irrigation area. Nevertheless, the required irrigation at each growth stage greatly varied in the different scenarios. More importantly, the jointing stage was the largest sensitivity to water shortage and the amplitude of water allocation variation. The main water supply source during tillering, jointing, and milk-ripe stages was surface water, while the main water source during heading was groundwater. Correspondingly, the multi-source configuration presented high effectiveness in the irrigation area, where the irrigation reliability fluctuated within the good and medium conditions. Fortunately, irrigation adequacy can widely be expected to serve great potential for improvement in the future. Consequently, the constructed model can be used to clearly represent the impact of dynamic variations in hydrological elements on the allocation of multiple water sources in the irrigation area. A relationship between canal water availability and field water distribution can also greatly contribute to a multi-water source configuration plan with simultaneous improvement of benefits and water efficiency. Particularly, the finding can provide strong decision-making support to the efficient use of agricultural water resources in the irrigation areas.
farmland; water resources; water cycle; efficient allocation; irrigation area; multiple water sources; random uncertainty
李茉,曹凯华,付强,等. 不确定条件下考虑水循环过程的灌区多水源高效配置[J]. 农业工程学报,2021,37(18):62-73.doi:10.11975/j.issn.1002-6819.2021.18.008 http://www.tcsae.org
Li Mo, Cao Kaihua, Fu Qiang, et al. Efficient allocation of multiple water sources in irrigation areas considering water cycle process under uncertainty[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(18): 62-73. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2021.18.008 http://www.tcsae.org
2021-02-21
2021-06-12
国家自然科学基金资助项目(52079029)
李茉,博士,教授,研究方向为农业水土资源高效利用。Email:limo0828@neau.edu.cn
付强,博士,教授,研究方向为农业水土资源高效利用。Email:fuqiang@neau.edu.cn
10.11975/j.issn.1002-6819.2021.18.008
TV213.4;S274
A
1002-6819(2021)-18-0062-12
