三维点云自适应稀疏优化重构

冯肖维，胡海云，庄睿卿，何 敏

（上海海事大学 电气自动化系，上海201306）

1 引 言

点云作为计算机图形学中的基本形状表示法，被广泛用于虚拟现实、环境感知、机器人导航和文物保护等领域［1］。

由于采集设备本身的测量精度和存在的各种外界因素，如光照、反射率和拼接误差等，原始点云数据会受到噪声和离群点的破坏。特别是当点云同时包含尖锐特征和较强幅度噪声的情况下，去噪过程变得越发困难，因为在某些复杂情况下特征很难与噪声进行有效区分；同时，原始点云数据不包含几何拓扑信息，所以没有先验信息来指导重构过程。因此，点云的重构是一项具有挑战性的任务，关键是如何在抑制噪声的同时恢复特征［2］。

近年来，针对三维点云重构出现了大量优秀算法。Alexa等［3］定义了点集的隐式曲面（Point Set Surfaces，PSS），利用移动最小二乘（Moving Least Squares，MLS［4］）将邻域点投影至局部拟合平面。为了避免MLS中的多项式拟合，Amenta等［5］直接利用质心的加权和光滑的梯度场来定义和计算曲面，在局部加权法向的基础上，通过邻域内样本的加权平均来实现点云的投影操作。但是MLS假设隐含面分段光滑，不可避免地导致几何特征变模糊。Guennebaud等［6］在PSS基础 上 提 出 了APSS（Algebraic Point Set Surfac⁃es），使用具有法向约束的球拟合，更好地适应不同曲率特征，当点云稀疏时也具有较好的处理效果，但是无法恢复拐角和棱边等尖锐特征。为了克服MLS对离群点的敏感性以及平滑尖锐特征的缺点，Öztireli等［7］结合移动最小二乘和局部核回归提出RIMLS（Robust Implicit MLS）方法，使其对噪声、异常值甚至稀疏采样具有鲁棒性。前述方法都是在局部邻域内进行的，当存在强噪声和离群点时，无法有效辨识噪声和尖锐特征。

近年来，全变分方法受到广泛关注，其思想来自于信号处理领域，通过度量与解的稀疏性相关的范数误差构建能量函数，实现信号的稀疏优化［8］。这类方法具有典型的全局特性，可以更好地在含噪信号中辨识尖锐特征。基于多数点云数据是分段光顺以及构成尖锐特征的点只占少数的事实，Avron等［9］将L 1稀疏表示引入点集的去噪过程中，通过直接使用一个重加权的L 1最小化过程对点集进行滤波重构，并实现特征的保持。此外，L 0优化同样是一种全变分方法，比起L 1具有更强的稀疏性，因此可以处理更高级别的噪声，如离群点等。受到Xu等［10］在图像去噪以及He等［7］在网格滤波研究的启发，Sun等［11］利用L 0最小化实现点云的降噪，虽然很好地保持了锐利的特征，但过度追求特征稀疏性导致平滑的曲面特征容易退化成分段平面。

前述方法要么无法有效保持锐利特征，要么可能在去噪过程中产生不自然的伪特征。为了克服这些局限性，本文提出了一种基于L 0稀疏优化的点云重构方法。整个过程大致分为3个步骤：首先，利用点的局部张量估计隐含面的几何属性，并通过成对一致性投票（Pair Consistency Voting，PCV）辨识特征点的局部最优邻域，在此基础上进行特征点法向的回归估计；然后，在L 0最小化的基础上引入自适应微分算子和投影正则项，实现不同特征区域点云的自适应降噪；最后，根据优化后的法向场对尖锐特征点进行投影恢复。本文所述算法的稀疏性介于L 0和L 1之间［12］，因此既可以处理具有明显尖锐特征的工件模型，也可以处理如雕像这类曲面特征占多数的模型。

2 特征点法向估计

法向蕴含曲面流型的局部几何信息，因此法向对点云的重构至关重要。原始点云不具有法向信息，需要进行可靠估计。

2.1 特征点识别

2.2 邻域鲁棒辨识

对于点云平坦区域的非特征点，基于各向同性采样的法向回归估计，如PCA（Principal Com⁃ponents Analysis）及其派生方法，可以获得稳定的计算结果。但是对于多个光滑流形面交界处，如拐角或棱边等特征，各向同性选择拟合数据区域导致法向估计受到多个不同邻近流形面上点的影响，法向估计并不稳定。为此，通常的策略是利用区域分割［15］或各向异性权重［16-17］找到具有相近法向点的局部邻域，或排除属于其他邻域面的点，从而获得更为可靠的法向估计。但是特征处点云可能伴随非均匀采样和大噪声，特征附近初始法向估计误差较大，因此选择离特征较远点的法向辨识邻域更加可靠。然而直接构造这样一个邻域并不容易，因为原始点云是无结构的。

为了选择一个最有可能不包含特征的邻域，本文首先利用成对一致性投票［15］进行特征点pfi∈Pf处隐含流形面的最大似然平面估计：

2.3 法向回归估计

3 点云稀疏优化重构

3.1 点云L 0稀疏降噪

通常点云隐含的流形面是分段光滑的，即除了形成尖锐特征的少数点，大部分点属于光滑区域。因此，可以利用尖锐特征点的稀疏性进行点云滤波，即稀疏低秩建模。Sun等［11］利用L 0最小化去除原始点云̂中包含的噪声：

上述表达式关于{pi}是二次的，因此可以通过稀疏最小二乘相关技术来求解。前述两步优化交替进行直到收敛，δ初始设置为0.02，在每次迭代中δ将被放大2倍，当δ接近无穷时，D(pi)j逼近θij。

前述点云L 0优化滤波在构建微分算子D(pi)j时假设局部邻域是平坦的，即某点及其邻域点应该在一个平面π(n∗i，pi)上，当点云中隐含曲面时，由于平面对曲面的非紧致估计，使得构建的微分算子会将曲率较小的曲面误认为是平面，从而对该曲面进行调整，使其逐渐退化成多个平面的组合，并在此过程中形成虚假边界特征，导致滤波后的点云发生畸变，参见图3（d）。本文通过自适应权重降低L 0优化的稀疏性，从而避免特征误判的发生，并依靠投影算子正则项来避免曲面特征退化成平面。

3.2 正则化滤波模型

为了更好地保持原始点云中的曲面特征，本文利用投影算子R(pi)j正则项和特征权重ωfij防止曲面特征在L 0最小化交替求解过程中发生退化：

其中，R(pi)j=n∗j⋅(pj-pi)，即利用邻域点的微切平面将特征点投影到由各邻域面所决定的隐含流形面上。如果点云局部区域是外凸的，该算子具有将点pi往外凸的方向调整的作用，从而防止曲面在微分算子D(pi)j作用下发生内凹退化成平面，参见图1。随着优化迭代的进行，点云中的噪声逐渐减小，特征变得光顺而无需过多调整，因此在每次迭代中，根据经验将正则项权重β乘以0.5，从而快速减小正则项在优化过程中的影响，在优化开始时赋予正则项较高的权重，并在优化后期将其效果降低，文中β初值取经验值0.1。

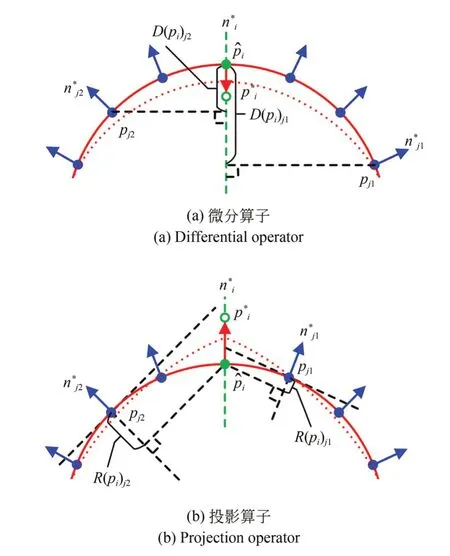
图1 不同算子作用下曲面调整Fig.1 Surface adjustment of different operator

此外，特征权重取：

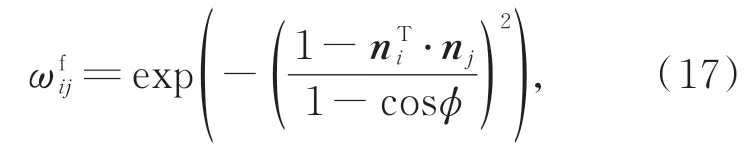
其中，参数φ为法向变化尺度，文中取经验值45°。该特征权重反映了点云局部弯曲程度，使其既可以在特征分类中增加平面、曲面与拐角等特征的区分度；又可以在实际二次优化降噪中避免由于噪声的非均匀性或调整时的非同步性而产生的伪特征点被保留，抑制虚假轮廓特征的产生。

3.3 尖锐特征恢复

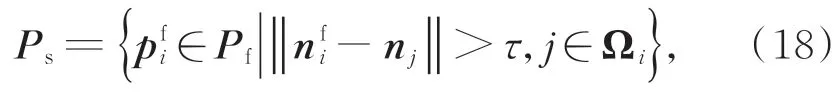
其中：nfi和nj分别是点pfi及其邻域点的单位法向，τ为夹角阈值，取经验值0.5～1。

特征边界上的点应该受到至少两个邻域面的约束，但是尖锐特征点在前述滤波过程中仅沿单一邻域面的法向进行调整，约束不足导致调整后的特征点不在各邻域面的交线或顶角上，故呈现锯齿状分布，如图3（d）和4（d）所示。为了更好地恢复尖锐特征，本文使用投影算子将尖锐特征点psi∈Ps进一步投影到隐含的特征边界上：

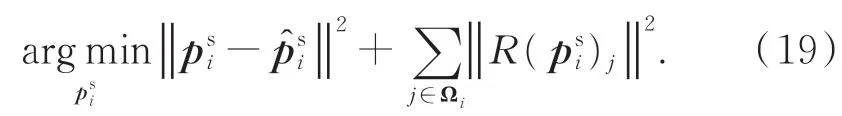
相较于文献［11］，本文所述尖锐特征恢复过程忽略了点psi处的法向约束，使得该点不限于在其切平面上调整，可以更好地恢复尖锐特征。

4 实验结果与分析

利用本文所述算法对测量和仿真的点云数据进行了滤波重构实验，并与现有主流算法进行了比较。实验程序采用C++语言编写，运行于Intel core i5-3.4GHz笔记本电脑上的Ubuntu 14.04 LTS操作系统。

4.1 邻域辨识与法向估计对比

图2展示了不同法向估计算法对图2（a）所示点云模型中顶角特征处邻域点的辨识与法向估计的结果。如图2（b），PCA法由于邻域是各向同性的，因此噪声和离群点影响了法向估计的精度和一致性。图2（c）为使用双边法向滤波［16］得到的结果，可以发现由于邻域点分布于多个邻域面上，且权重考虑了初始法向，导致特征处的法向估计不稳定，存在较大方差。Wang等［17］提出的加权迭代回归法同时考虑法向、距离与离差3个因素，保证只有来自于同一个流形面的邻域点对于法向的估计产生重要影响，但依然会对离群点分配小的权重，且为了得到良好的法向估计结果需要考虑多个带宽参数，当噪声较强时，带宽难以确定，如图2（d）。图2（e）是本文所述方法得到的邻域和估计的法向，可以发现加权回归估计配合正确的邻域得到了更加一致的法向分布，且能够有效估计尖锐拐角特征处的法向。

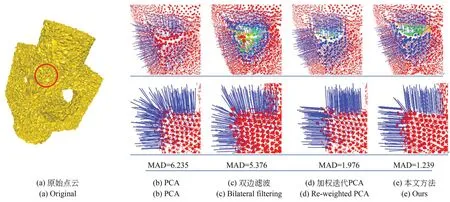
图2 邻域点辨识与法向估计比较Fig.2 Comparison of neighbor points identification and normal estimation

为了进一步对法向估计的准确性进行量化评价，首先对理想点云模型进行三角网格划分，然后利用去噪点云模型P∗和理想网格模型M法向间的平均角度误差（Mean angular deviation，MAD［1］）作为评价指标：

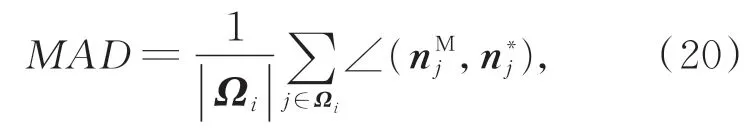
4.2 典型算法处理效果对比

图3和图4显示了本文所述方法与APSS［5］，RIMLS［6］，L0［11］3种 典 型 算 法 间 的 重 构 效 果 对比。为了便于观察，对点云进行了渲染处理。由于APSS使用移动最小二乘法拟合球面进行投影重构，因此在圆弧特征部分都实现了比较精确的还原，但是无法恢复尖锐的特征。RIMLS使用核回归进行曲面鲁棒重建并考虑到特征的保持，因此在图3（d）中模型的边缘轮廓部分恢复效果较好。但是当噪声较强时，光滑区域依然存在缺陷。由于L 0的稀疏特性，尖锐特征被有效保留，但是曲面特征被抑制，如图3（e）在两端圆柱部分以及圆孔部分都产生较大的畸变。本文方法不仅保留了精确的尖锐特征信息，对于曲面特征滤波效果良好，具有较好的特征保持能力，如图3（f）所示。

图3 真实点云重构效果对比Fig.3 Comparison of reconstruction effects of real point clouds

4.3 重构误差与耗时定量分析

为了量化比较各种算法的处理效果，本文利用图4所示仿真二面角和圆柱体的理想点云模型，与加噪滤波后的重构点云模型进行定量误差分析［1］。加噪点云模型是在理想点云模型上加入沿法向方差为0.4倍一环邻域点平均距离的高斯噪声。

图4 仿真点云重构效果对比Fig.4 Comparison of reconstruction effects of synthetic point clouds

为了量化点重构的位置误差，通过网格模型M和去噪点云模型P∗之间的离差作为评价指标：

其中：A i是三角网格M中某个三角面的面积，dist(p*i，Tc)是某个重构的点p∗i∈P∗到网格模型中最近三角形Tc∈M的垂直投影距离，M1-ring(i)为点p∗i的一环邻域面集合。

针对二面角和圆柱体两个模型进行Ep和MAD两种误差分析，图5显示了图4各种滤波重构算法迭代过程中Ep和MAD的变化情况。可以发现随着迭代次数的增加，Ep和MAD的误差逐渐减小，无论是具有尖锐特征的二面角模型还是具有曲面的圆柱体模型，本文所述方法的重构误差是最小的。与传统的L 0点云滤波重构算法［11］相比，经过本文所述算法处理后点云模型的重构误差Ep平均减小10.2%，法向误差MAD平均减小29.7%。

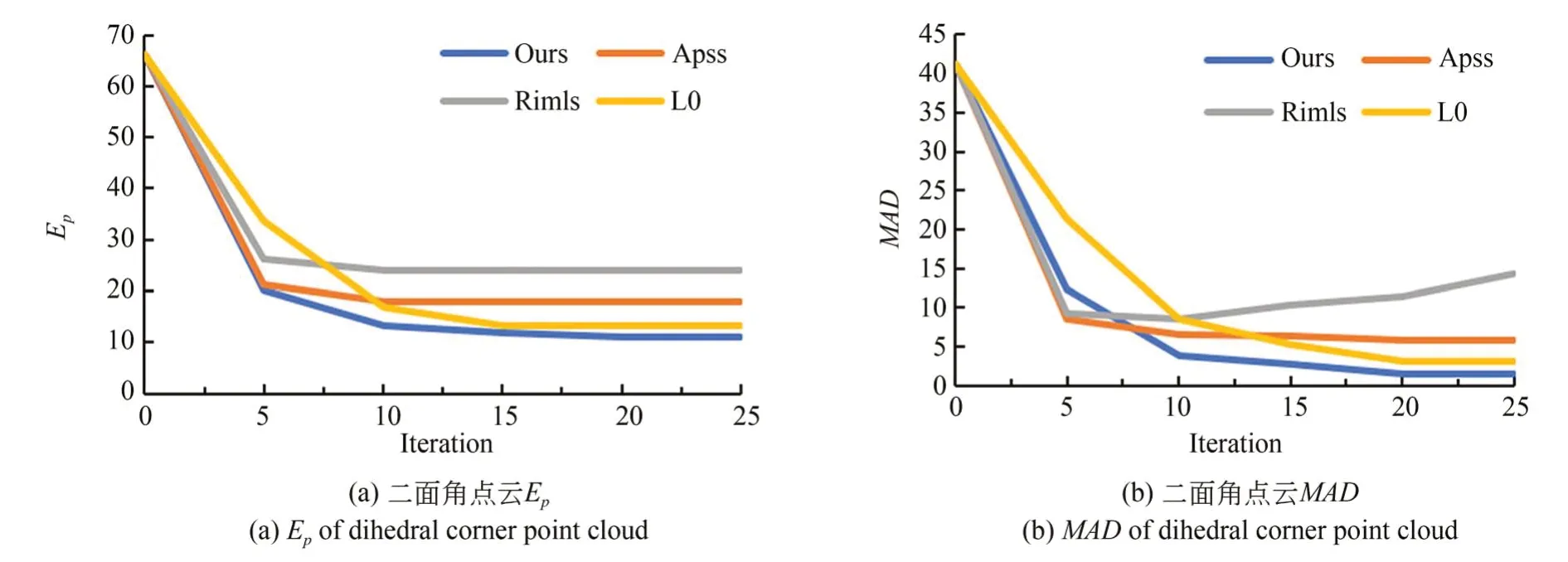
表1显示了图4各种算法滤波重构的耗时统计。由于APSS与RIMLS为局部优化法，因此在时效性上要优于基于全局优化的L 0与本文所述方法，本文所述方法耗时略高于3种典型方法中重构精度最高的L 0法。

表1 算法耗时统计Tab.1 Time consumption statistics of different algo⁃rithms

5 结 论

本文提出了一种基于L 0稀疏优化的点云重构方法。引入鲁棒统计的思想实现特征处邻域的有效辨识，增加法向估计的准确性。为了解决平面微分算子对于曲面特征的非紧致估计，通过投影算子正则项解决L 0优化交替求解过程中曲面特征过度调整而产生的畸变，并利用考虑点云局部几何特性的自适应微分算子，避免L 0优化过度追求稀疏性，而产生虚假边界轮廓。根据优化后的法向场对点云中尖锐特征进行辨识，凭借投影算子对尖锐特征点进行优化恢复。本文所述方法可以有效提高点云的质量，相比传统L 0点云滤波重构算法，重构后点云的误差平均减小10.2%，法向误差平均减少29.7%，同时视觉效果优于现有典型算法，为基于点云的计算机三维测量与逆向建模提供一种有效预处理方法。

在今后的研究中，可以考虑引入基于曲面模型的微分算子，更加准确判断特征边界，在提高曲面特征恢复能力的同时增加算法的收敛速度。