河流自然水体中三维视觉测量

许 丽，周永昊，陆桂明，周金峰，张 帆，罗文宇

（1.华北水利水电大学 物理与电子学院，河南 郑州450011；2.中国移动通信集团公司，北京100033）

1 引 言

我国河湖资源丰富，建国以来已建设了大量的水利工程。水利工程作为国民经济的重要基础设施，在防灾减灾和缓解水资源供需矛盾等方面发挥了重要的作用。由于各类水工结构长期承受水压和温度等诸多因素的影响，大量水利工程出现了不同程度的裂缝、渗透、磨损等安全问题。准确及时地获取水工结构形变和缺损信息非常必要，特别对水下水工结构的形貌探测尤为重要［1-2］。

目前对河流水下形貌探测的方法主要有基于声学的方法和基于视觉的方法。基于声学的方法主要用来估计目标物体的大致大小、确定目标与声纳的距离，用来进行水下地形大范围三维信息获取和水下目标定位［3-4］；视觉测量方法在近距离、高精度、实时性作业场合有着独特的优势，在水下探测领域中占据着重要的地位［5］。

结构光技术作为视觉测量的常用方法之一，被广泛应用于逆向工程、文物三维重建、工业三维检测等多个领域［6-8］，但在河湖水下形貌探测的应用较少。结构光技术是基于光学三角法测量原理，由投射器将一定模式的结构光投射于物体表面形成特征点，根据CCD摄像机拍摄到的图像，并依据光学三角约束关系，获取目标物体的三维信息［9-10］。影响结构光三维测量精度因素有测量图像中有效信息的提取精度和三维模型的准确性［11］。河流自然水体环境对视觉测量的影响有两个方面：其一，水中大颗粒悬浮粒子、浮游生物所引起的散射造成水下测量图像退化严重。前向散射导致细节模糊，纹理信息丢失；后向散射导致图像对比度降低，图像出现雾化模糊现象，进而引起特征点提取困难问题［12-13］。其二，水下视觉测量设备多被封闭在玻璃等透明材料内，光线经历空气-玻璃-水三个传输阶段。多次折射过程使得视觉测量由线性过程变换为非线性过程［14-15］。

为了提高水下视觉三维测量的精度，专家们进行了大量研究。哈尔滨工业大学王宗义教授在水下测量时利用激光三角法的原理进行折射补偿，将摄像机拍摄水下物体时的被测点补偿到陆上三维坐标系下［16］。中国海洋大学解则晓教授对水下光平面的偏移和像点坐标进行修正，采用折射补偿的方式通过陆上标定参数完成水下目标测量［17］。这类方法一般情况下只能作近似测量，难以得到较高的测量精度。Fan H假设虚拟对象点位于真实对象点的正上方，建立虚拟物体点与真实物体点之间的几何关系，并在此基础上建立了基于“虚实”关系的平面折射模型［18］。标定过程多采用空气和水下标定相结合的方式进行，增加了模型参数的个数和标定实现难度。

针对自然河流水体中视觉测量存在水下成像质量差、多介质光线出现多次折射现象和测量过程相对静态等特点，本文提出了基于折射的水下视觉测量模型；采用蒙特卡洛模拟方法，分析了自然水体像点误差对该模型计算精度的影响。利用黑白条纹对水下背景噪声的高鲁棒性，结合水工结构形貌探测相对静止的情况，提出了径向多条纹模式编解码方法；该模式的编解码方法在牺牲一定的时间分辨率的代价下，适应自然水体中浑浊成像条件，获得密集的三维形貌数据。建立了水下视觉测量系统，在1 500 mm的测量距离上对水下瓷瓶进行三维形貌测量，在清水、含有40，60和90 g泥沙的浑水中可以获得平面残差分别为0.95，1.93，5.43和21.43 mm的测量结果。

2 自然水体中的水下视觉测量模型

在水下形貌视觉测量过程中，水下物体表面反射的光线由水中传入摄像机时需要通过水体、玻璃罩和空气三种介质。由于水、玻璃、空气三者折射率不同，光线发生多次折射现象，传统透视投影模型己不适用于水下测量。

2.1 基于折射的水下视觉测量模型

如图1所示，oxyz为摄像机坐标系，OXY为摄像机像平面坐标系，lw，lg和la分别为成像过程中水中入射光线、玻璃中折射光线和空气中折射光线的方向矢量。lpa，lpg和lpw分别为空气中投影入射光线、玻璃中折射光线和水中投影折射光线的方向矢量。Np(a，b，c)为折射平面π1归一化法向量参数。W为玻璃介质的厚度，na，nw和ng为空气、水和玻璃的折射率。

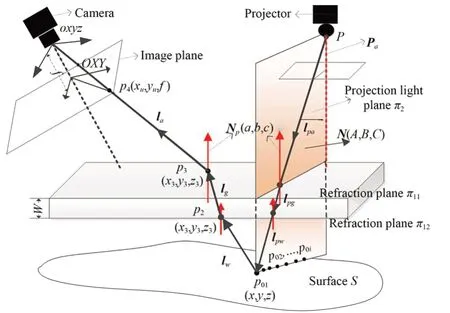
图1 基于折射的水下测量模型Fig.1 Model of underwater measurement based on re⁃fraction

在投射过程中，空气中投影仪投射光线lpa到折射玻璃面，经过多次折射后到达水下被测表面S。当投影仪投射光轴Pa垂直折射平面π11投射，投射光轴Pa与折射平面法向量Np平行。投影光轴Pa与投射光线lpa相交于投影中心P。因此，投影光轴Pa、投影入射光线lpa和投影折射光线lpg三线共面于投影光平面π2。也就是说，当投影设备垂直于折射平面π1投射（即投射光轴lpa垂直于折射平面π11，且通过投射光平面π2）时，玻璃中投射光平面和空气中投射光平面共面。假设玻璃上下折射面相互平行，两个折射面的法线方向均为Np。根据多次折射分析，投影入射光线lpa和投影折射光线lpw位于折射平面法线Np的两边，且三线共面，即水下投射光平面、玻璃中投射光平面和空气中投射光平面为同一平面［19］。n(A，B，C，D)为投影结构光平面π2的归一化法向量参数。投影光平面π2与水下物体表面的交点p01，…，p0i为水下物体表面上的被测点。

以被测点p01（x，y，z）为例，分析其成像过程。经点p01反射的光线经过界面π11和π12两次折射后，成像于摄像机像平面上点p4，入射光线与折射上下平面交于点p3和p2。物点p01和点p2构成水下入射光线lw，交点p3和p2构成玻璃内折射光线lg。

空气中成像光线传播路径中的折射矢量la可由被测物点的像点p4（x u，yu，f）与摄像机原点o表示为op4。折射平面交点p3（x3，y3，z3）可由成像折射光线la和折射平面π11相交得到。

当玻璃上下折射面相互平行，两个折射面的法线方向同为Np(a，b，c)。根据Snell定律的矢量形式，玻璃中光路lg和空气中光路la之间的关系为：

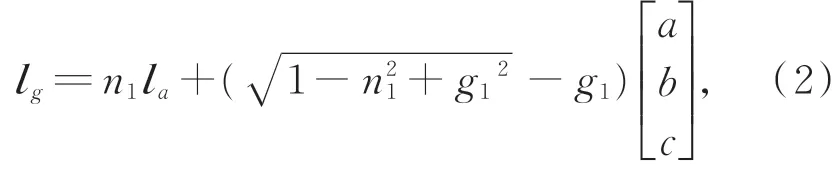
经过相互平行两折射面后，入射光路lw和折射光路la之间的关系为：

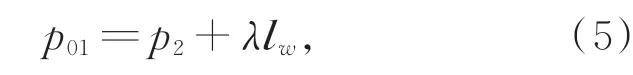
其中，λ为比例系数，由被测物点的位置决定。投射光平面π2与水下入射光路lw相交于被测物点，即p01=lw∩π2，由此可得出公式（1）中的比例系数λ为：

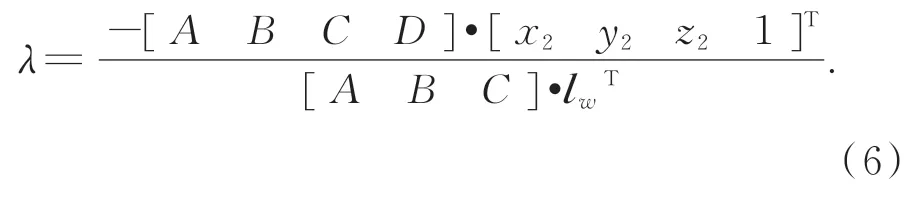
水下被测点p01（x，y，z）可表示为：

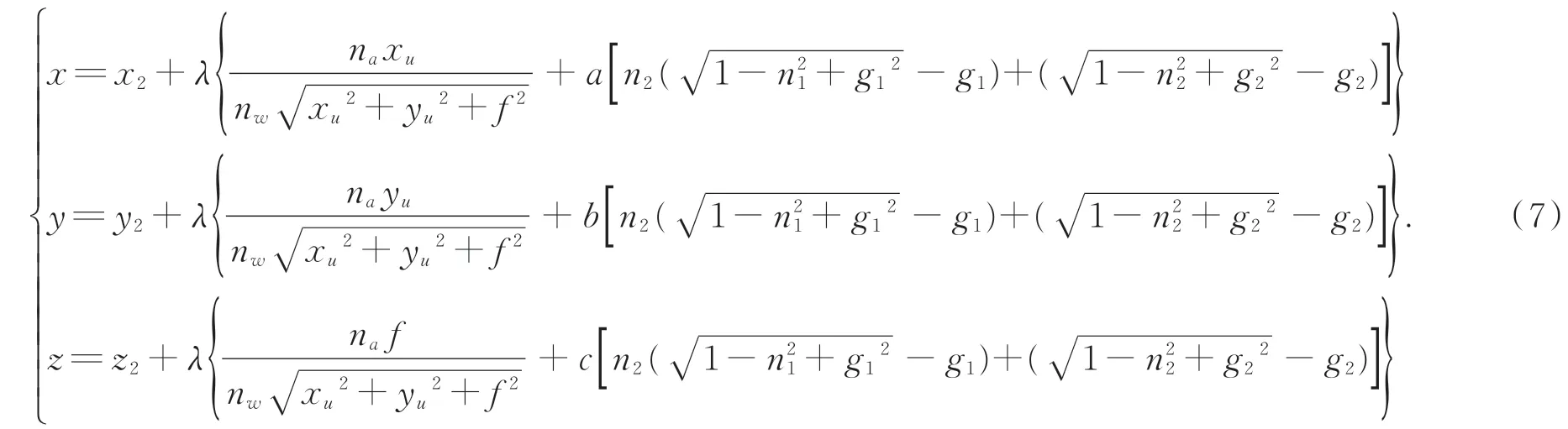
2.2 自然水体环境对三维测量精度的影响

根据以上公式可知，水下三维测量精度受限于像点坐标（x u，yu）、相对折射率n、相机焦距f、折射 平 面 和 光 平 面 法 向 量（Np(a，b，c，d)，N(A，B，C，D)）等参数的获取精度。像点坐标和相对折射率误差主要来源于自然水体环境；相机焦距、折射平面和光平面的参数误差来源于标定过程。这里主要分析自然水体环境对三维测量精度的影响，采用蒙特卡洛统计分析方法，对测量模型中三维测量坐标相对于图像坐标（x u，yu）误差的鲁棒性进行分析。在每个参数上加入的不同相对均值和方差的随机噪声，计算10 000次以上，分析同一方差下三维点云坐标计算相对误差随噪声相对均值的变化情况。

如图2所示，当图像坐标（x u，yu）加入相对方差为0.1的噪声时，三维点云的计算误差相对均值为0.1。当图像坐标（x u，yu）加入相对方差为0.1和相对均值在［-0.1，0.1］范围内的噪声时，三维点云的计算误差相对均值约为0.06。假设图像坐标真实值为（1 000，1 000）pixel，像点提取误差为5 pixels（相对误差为0.005），测量相对误差为0.04。当测量距离为1 500 mm，可以得到误差均值为60 mm的点云计算结果。加大图像坐标（x u，yu）噪声的相对均值和方差时，三维点云的计算误差明显增大。

图2 像点提取误差对三维测量误差的影响Fig.2 Error analysis of 3D measurement due to image point extraction error

根据以上分析可知，自然水体引起点云坐标计算误差主要来源于水下图像模糊所引起的像点坐标提取误差。在2 000 mm以内的测量距离上进行河流水下三维视觉测量，只要像点提取相对误差在10%以内，可以获得误差在±1 dm以内三维点云计算结果。

3 自然水体中投射模式设计与解码

3.1 投影编码光设计

根据编码光设计的不同，编码光可被分为强度编码光和相位编码光两大类。强度编码光包括散斑编码光［20］、多线编码光［21］和二值编码光（如空间编码的DeBruijn码［22-23］和时间编码的格雷码［24］）；相位编码光包括单频正弦光栅［25］和复合正弦光栅［26］。其中，二值编码光是误差最小的编码方式，对成像条件和图像质量具有良好的鲁棒性和抗噪性，被广泛地应用到工业零部件检测、逆向工程、文物数字化等应用领域。

由于光线在自然水体中存在严重的衰减和散射等现象，水下图像存在图像模糊、特征提取困难等情况，本文设计黑白交错中心旋转径向多线编码光模式。如图3所示，以黑白边缘作为测量条纹，以水平边缘S1作为参考轴，按逆时针顺序依次间隔45o为条纹S6、S11和S16；将图3（a）投影模式按逆时针方向依次旋转9°，18°，27°，36°得到图3（b）、（c）、（d）和（e）中的中心旋转投影编码光模式；5场投影模式中每隔9°得到一条条纹线，可以获得20条条纹，与投影中心P构成20个光平面。

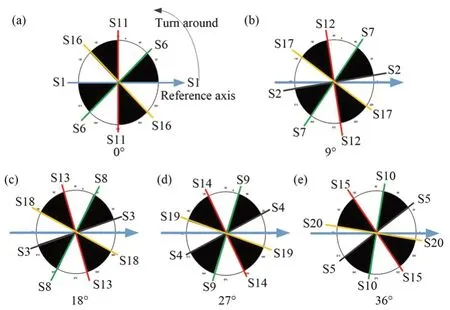
图3 结构光系统投影模式设计（a）基准投射模式；（b）～（e）多场中心旋转投影模式Fig.3 Design of projection model in structured light sys⁃tem（a）The model of projection；（b）～（e）Multi-field center rotation projection models

对单场投射而言，相邻结构光条纹的夹角为45o，可增大条纹边缘解码的容错性，适应水下降质图像的特点，降低了条纹的误匹配率；结合河流水下形貌测量多为静态测量的特点，采用多场次投射，获得多条测量条纹，提高了对被测物体的扫描分辨率，可以更好地获取被测物体的形貌特征。

3.2 浑水图像的条纹解码

在多条纹结构光模型中，一条条纹对应一个测量光平面，条纹的正确提取和解码在结构光测量过程中至关重要。由于自然水体中颗粒物对投射光源的散射作用，水下图像存在雾状模糊、对比度下降等现象，对准确获取物体表面特征信息造成干扰。

投影仪投射的编码条纹图像为多场共点的条纹簇，采用极坐标下的条纹表达式来描述条纹，利用各个条纹相对于参考轴的夹角解码条纹。如图4所示，浑水图像的条纹解码过程分为极坐标参数校正、浑水图像清晰化预处理、条纹提取和解码四个步骤。

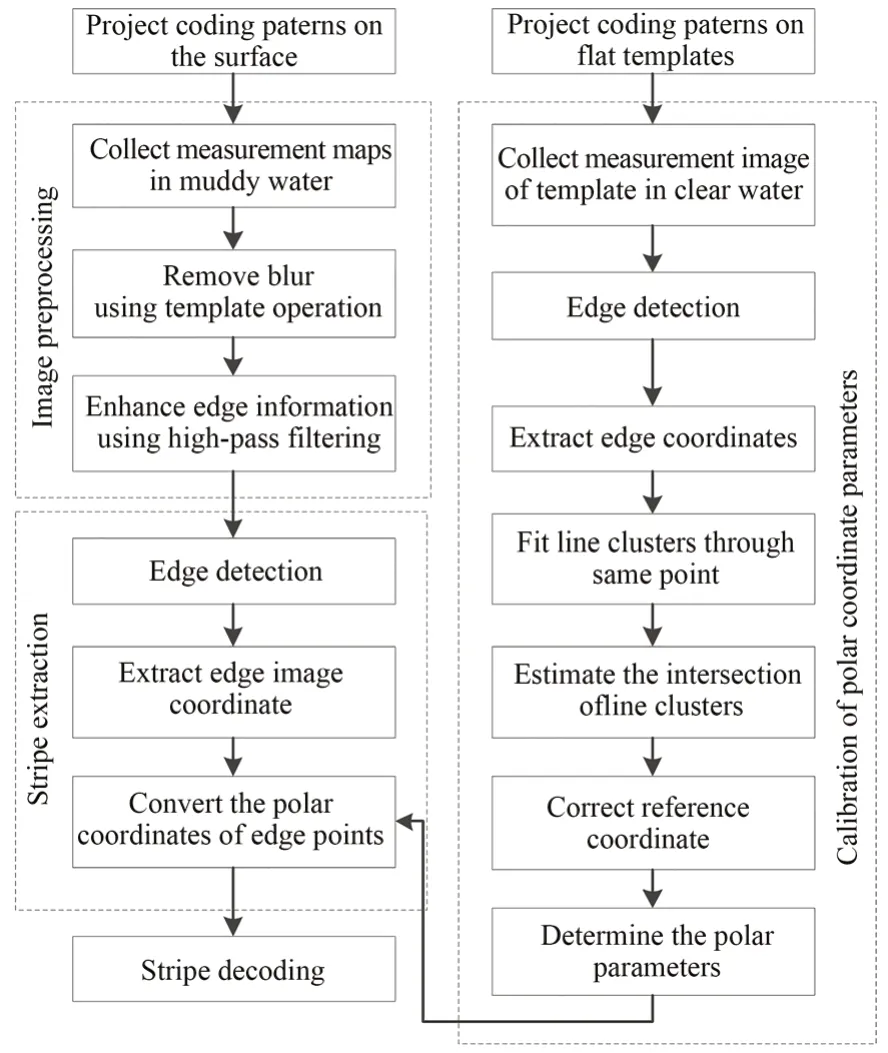
图4 浑水图像的条纹解码过程Fig.4 Stripe decoding of image under turbid water

第一步：极坐标参数校正

建立条纹簇的极坐标系需要事前确定极坐标中心和参考轴。首先，在清水中投射编码模式，采集平面模板的测量图，提取条纹边缘像点。采用牛顿迭代法，拟合对应的条纹直线簇。利用优化运算的方法，估计出直线簇的交点，即为条纹极坐标的中心。

在本文折射测量模型中，投影仪垂直投射，摄像机倾斜拍摄。对编码条纹进行解码前，需要校正成像面的极轴。采集第一场编码光图像，选取分布±45°两条直线上的条纹像点。根据像点信息，拟合出条纹像点所在的直线方程。利用两直线倾角δ1和δ2，以倾角为（δ1+δ2）/2过交点的直线作为极轴。

第二步：去除浑水图像的雾状模糊

事先向当前水体中投射全白模式，分析采集图像的特点，获得图像雾状模糊模板；利用模板运算削弱浑水图像的雾状模糊；采用高通滤波的方法，加强条纹边缘信息。

第三步：条纹提取

对预处理后的水下图像进行边缘检测，提取条纹边缘像素点。利用标定过程中所估计出径向多线条纹的交点作为极坐标中心，将像素点坐标转为极坐标值，建立条纹解码极坐标系。

第四步：根据极径和极角对条纹进行解码。

单场条纹图中，条纹间隔角度均匀分布于180°范围内，相邻条纹间最大角度偏移量为45°。这里相邻条纹间偏移范围选取（-20°，20°］。通过5场投影编码图获得20条测量条纹。5场编码图得到相邻条纹间的角度间隔为9°。

如图5所示，以第一场测量图为例，四条参考条纹的倾角分别为0°，45°，90°和135°。四条条纹角 度 范 围 分 别 为（-20°，20°］，（25°，65°］，（70°，110°］和（115°，155°］。判断测量像点在极坐标系上极角θp符合的区间范围为对应的条纹编码（光平面序号）。图中黑点表示测量图中的有效像点，红色星点表示无效像点。测量像点A1和A2的极角分别为θ1和θ2，θ1和θ2均满足角度区间（-20°，20°］，被判别为条纹S1上测量点；测量像点A3的极角θ3满足角度范围（25°，65°］，则被判断为条纹S2上的测量点；测量像点A4的极角θ4不满足以上四个角度范围，被视为无效像点。

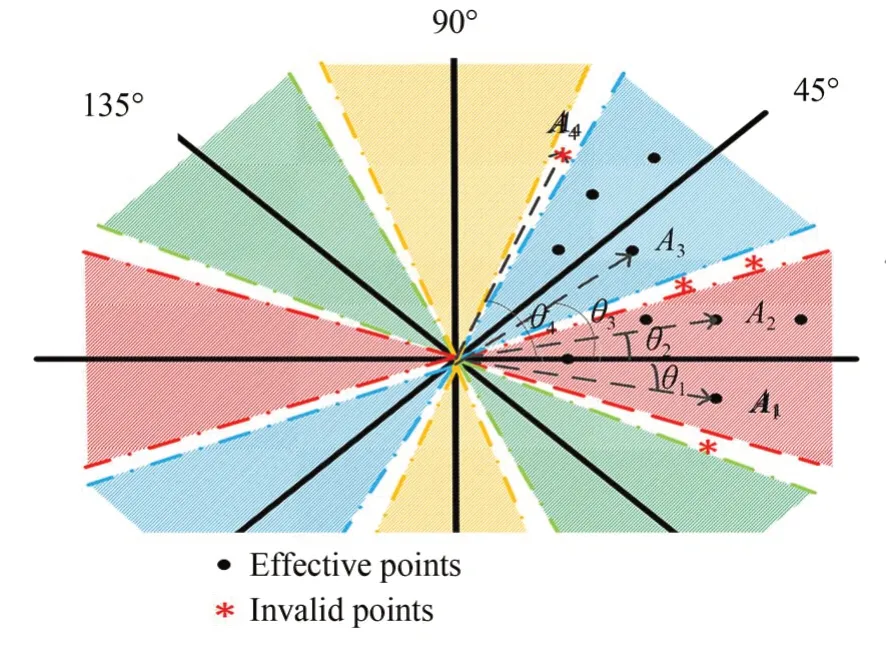
图5 第一场测量图的条纹解码规则示例Fig.5 Example of stripe decoding rules for the first field measurement pattern

以上分析可得，第i场投影编码图像中，第k条条纹上像点的解码规则为：

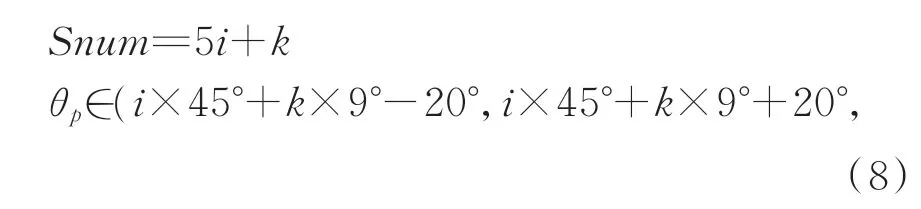
其中：Snum为第k条条纹的解码值，θp为测量像点的极角，p为测量像点的序号。

4 水下结构光系统参数标定

根据公式（7）所示，水下被测点p01（x，y，z）坐标计算公式中需要事先确定的参数有玻璃介质的厚度W，空气中、玻璃中和水下的折射率（na，ng和nw）；需要事先标定的参数有相机光学参数（焦距f、平移向量T和旋转矩阵R）、折射平面参数Np(a，b，c，d)和光 平 面参数N(A，B，C，D)。因此，水下结构光系统标定共分为三部分。

第一步：摄像机参数（相机焦距f、畸变系数k和外部参数（R和T））的标定。由于摄像机内外参数受成像环境的影响不大。这里采用空气中的相机标定方法，利用空气中靶标平面上已知特征点完成摄像机参数标定。

第二步：投影光平面参数（N(A，B，C，D)）标定。根据以上水下视觉测量模型可知，当投影光轴垂直于折射平面，且通过光平面时，水下投射光平面和空气中投射光平面共面，可利用空气中光平面参数的标定方法进行水下投射光平面参数标定。投射光平面和被测物体表面相交曲线上的点即为测量点。由于测量点的任意性，无法事先得到各个光平面上的标定点。本文采用交比不变法，利用靶标上的已知特征点间接求得标定点的三维坐标。通过多次获取结构光平面上的多组标定点完成光平面参数标定。

第三步：折射平面参数（Np(a，b，c，d)）标定。结构光视觉系统在水下测量过程中常将投影设备和成像设备封闭在透明箱体中，折射平面的标定可借助结构光系统在空气中对投射平面的测量数据进行。通过计算出来的折射平面上测量点，优化估计折射平面参数。这里暂不考虑水下环境对折射平面参数的影响。

4.1 摄像机参数标定

摄像机标定采用基于径向排列约束的两步标定算法对摄像机参数进行标定［27］。由摄像机采集棋盘格图像，采用角点检测算法提取棋盘格中的角点像坐标。以棋盘格平面靶标的中心建立世界坐标系，利用已知的靶标上角点坐标和对应的像坐标求解摄像机内外参数，其中靶标角点世界坐标和像坐标分布如图6所示，得出的摄像机标定参数如表1所示。

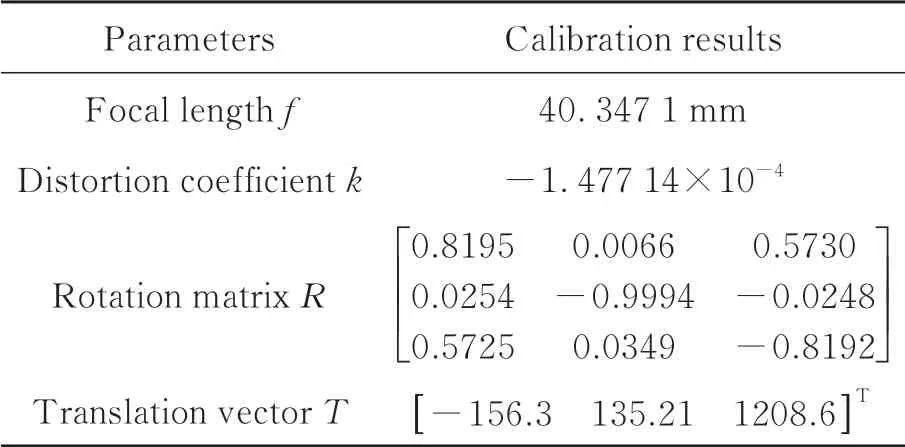
表1 摄像机标定参数Tab.1 Camera calibration parameters

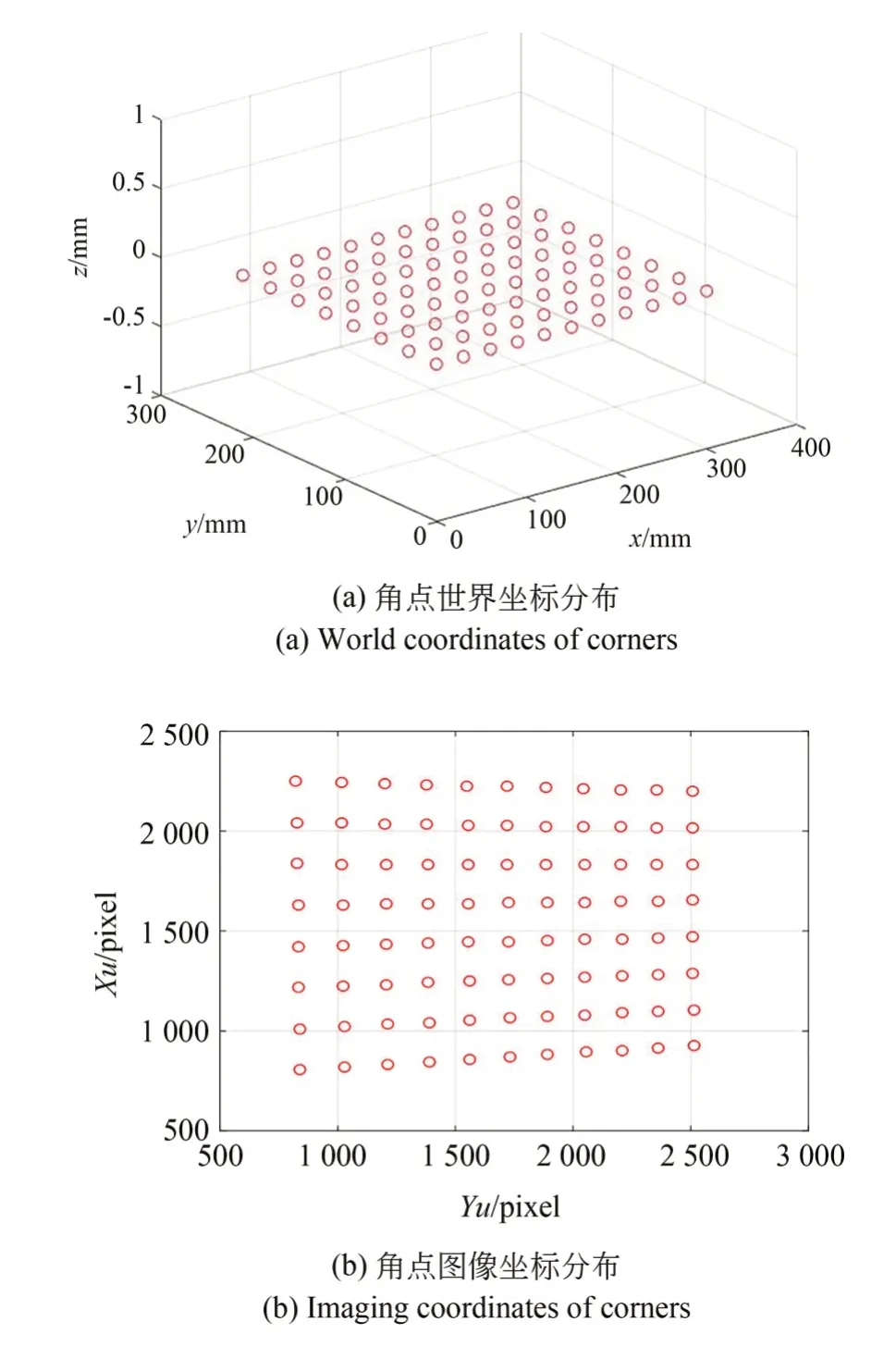
图6 棋盘格平面靶和角点的世界坐标和像点坐标Fig.6 World coordinates and imaging coordinates of cor⁃ners on planar target with checkerboard

4.2 光平面参数标定

4.2.1 标定点计算

如图7，光条纹投射到平面靶标上为直线L2，E 1，E 2，E 3为平面靶标上位于直线L1上的特征点，它们在世界坐标系下的坐标分别为E1（x w1，yw1，0），E2（x w2，yw2，0），E3（x w3，yw3，0），与特征点相对应 的 图 像 点 为e1（X u1，Y u1），e2（Xu2，Y u2），e3（X u3，Y u3），光条纹与靶标平面上共线特征点所在直线的交点E x（x w x，yw x，0）为标定点，其对应图像点为ex（Xux，Y ux）。在像坐标系下，通过求解特征点所在拟合直线和光条纹所在拟合直线的交点，得到标定点的像点坐标ex。根据交比不变原理可知［28］：

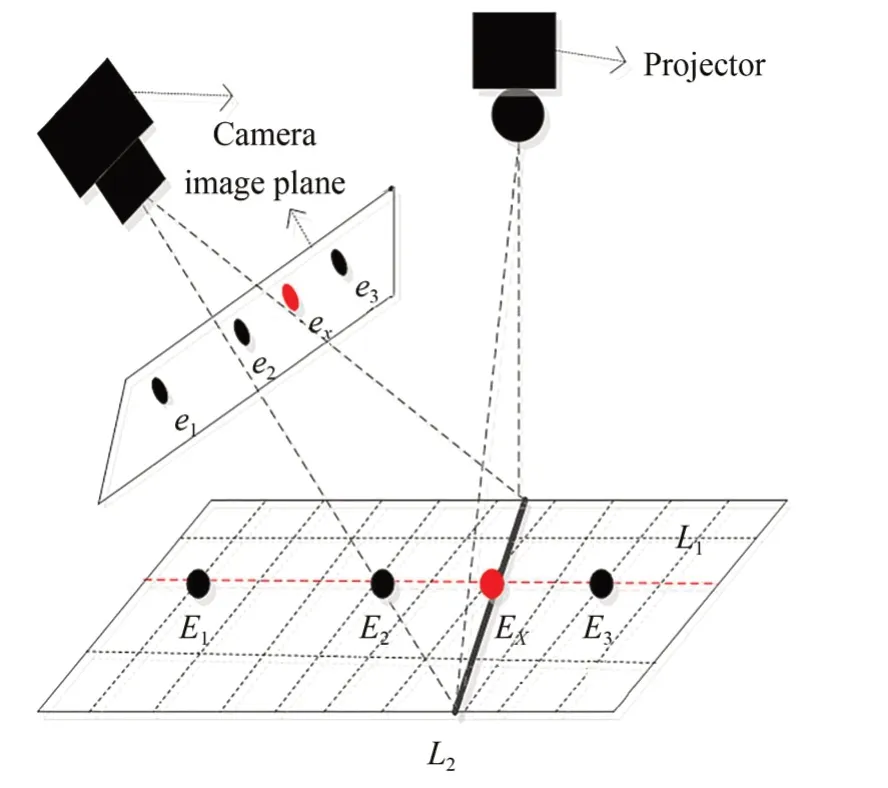
图7 光平面标定原理Fig.7 Principle of light-plane calibration

标定点在世界坐标系的坐标为：

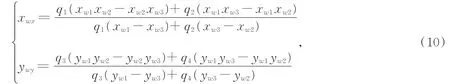
其中：

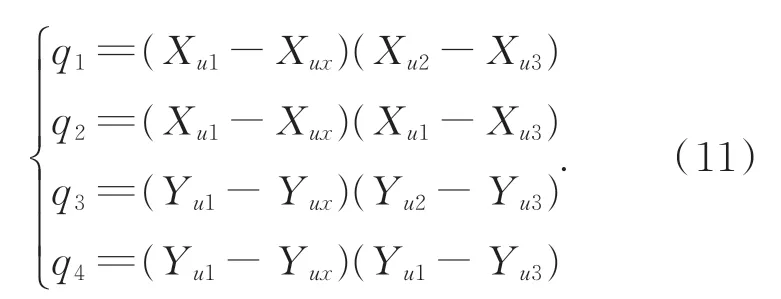
在实际计算中，参与交比计算的特征点只有3个，所以计算结果很容易受到特征点噪声影响。为了克服噪声影响，所选取的靶标上共线特征点数N多于3个，通过计算C3N个特征点，然后求取均值得到该标定点的坐标值。

4.2.2 光平面参数估计

由光平面建模可知，光平面方程可用线性方程组求解表示：

其中：M j×3为标定点所构成的系数矩阵，j为标定点的个数（j≥3），E为单位向量。为了保证所求光平面参数的准确性，使用多组标定点采用非线性优化迭代的方法对光平面参数进行求解。系统中涉及的光平面参数如表2所示。

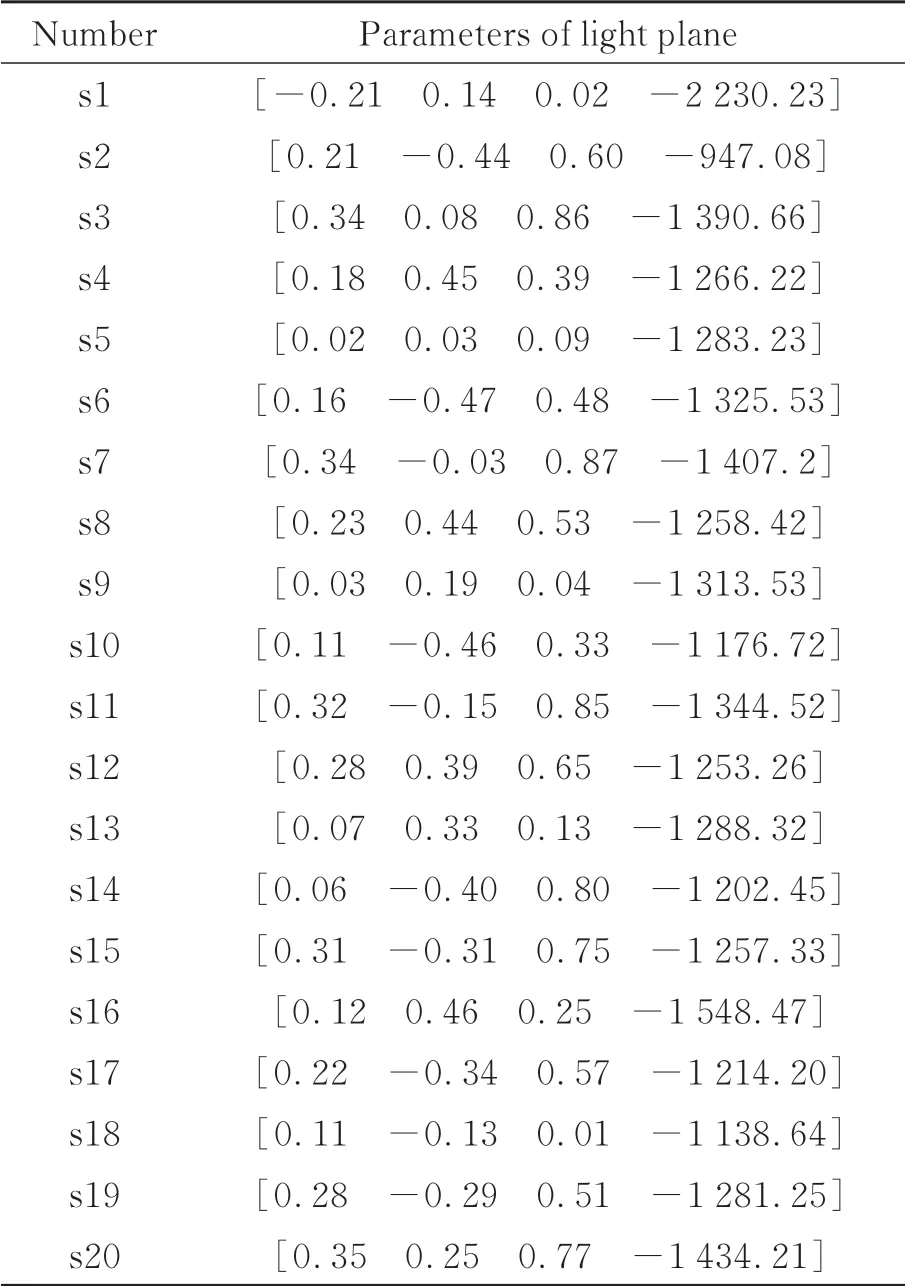
表2 投影光平面参数Tab.2 Parameters of light-plane

4.2.3 折射平面参数标定

利用已经建立的视觉测量系统对空气中的折射平面进行三维测量，通过采集折射平面上5100个测量点，求得折射平面参数为：

5 自然水体中三维视觉测量实验分析

5.1 水下视觉测量实验

如图8所示，水下视觉系统由尼康D90摄像机（最高分辨率为4 288×2 848）、爱普生CHTW610的投影仪（亮度为3 000 lm，标准分辨率为1 920×1 028，对比度为15 000∶1，投影尺寸为30～300英寸）组成。在标定中使用电动三维平移台（重复精度5μm，分辨率2μm）和平面靶标（9×12个黑白相间的小方格，每个方格尺寸为30×30 mm），平面靶标的加工精度为0.05 mm，相机和投影仪固定在支架上，其二者光轴夹角约为30°。假设水箱折射平面平整，利用水平仪测得折射平面倾角为α，设置投影仪垂直投射，调节投影仪支架倾角为90°-α，保证投影仪垂直投射到折射平面上。水箱厚度W为7 mm，水箱尺寸为1 m×1.2 m×1 m，物体被放置在注水的水箱里，在水中加入泥沙模拟河流自然水体环境。空气中折射率na为1，水中折射率nw为1.33，水箱玻璃的折射率ng为1.66。

图8 水下结构光系统构成Fig.8 Components of underwater structured light system

5.2 清水中视觉测量实验分析

为了排除水体浑浊对三维测量的影响，本实验先在清水条件下获取物体的三维形貌，以便分析在本课题中所建立的水下视觉测量折射模型的可行性，为后期在自然水体下对物体进行三维测量奠定理论基础。

将瓷瓶放置在装满清水的实验玻璃水槽内，其测量距离估算为1 500 mm，将图3中设计的五场模式结构光模式以垂直折射平面的方式投射到瓷瓶表面上，摄像机采集到带有结构光投射模式的图像（如图9）。通过线缆将图像传输到计算机内，在计算机提取图像中所包含的光条纹信息，依据2.1节的水下视觉测量折射模型，获取瓷瓶表面的三维信息。

图9 水下瓷瓶测量图像序列（a）～（e）5场投影模式的测量图像序列Fig.9 Underwater image acquisition sequence（a）～（e）Measurement images of projection period with five fields

在每一场模式结构光投射下，会有4个光平面，共存在20条光条纹。为了更直观的展现所提取条纹的位置分布，选择用极坐标的形式来存储和记录光条纹的信息。由于越靠近极点的位置，其光条纹分辨率越低，越容易造成光条纹提取的计算误差，为了减少这种误差，用极径r≥10 pix⁃els范围内的光条纹信息点去获取瓷瓶表面的三维点云。单场提取的光条纹和五场一共提取的光条纹分布分别如图10（a），10（b）所示，同一颜色代表同场投射中的4条光条纹，不同颜色代表不同场次投射下的光条纹，每一条光条纹代表着一个投影光平面。利用测量得到的三维点云进行表面拟合，生成被测物体表面如图10（c）所示。

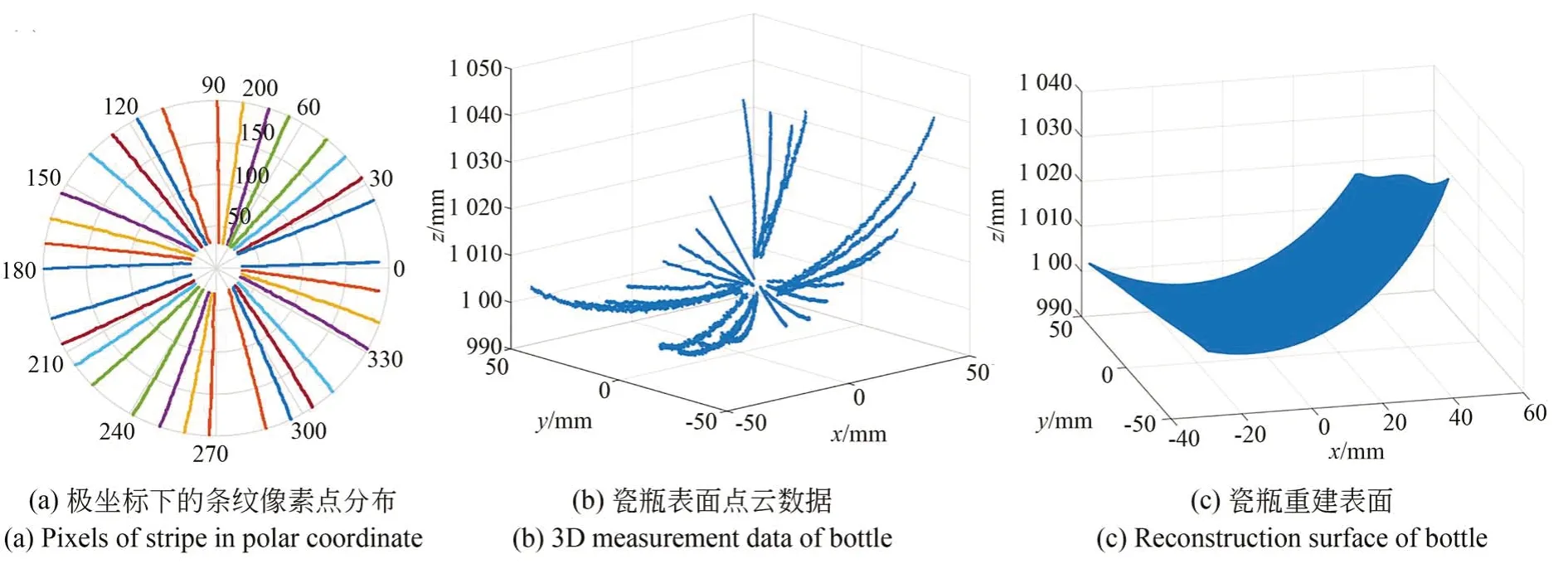
图10 水下瓷瓶测量过程Fig.10 Underwater measurement process of bottle

5.3 浑浊水体中视觉测量实验分析

为了实验分析浑浊水体对水下三维形貌测量的影响，这里在1 m×1.2 m×0.8 m的水体中加入不同重量的泥沙，在1 500 mm的测量距离上，分别对不同浑水条件下的平面物体进行三维形貌测量。由于水体浑浊所引起的图像退化影响图像测量点的坐标提取和解码误差，最后影响到三维测量的计算精度。本文从浑浊水体对图像条纹提取和解码的影响，以及对三维测量精度的影响两方面进行实验分析。

5.3.1 浑浊水体中条纹提取和解码

以第一场测量过程为例，选取清水和含有40，60和90 g泥沙的三种浑水条件进行实验分析。由于浑水泥沙颗粒所引起的图像雾状模糊，图像从清晰度、黑白条纹对比度等方面有明显退化，提取的条纹边缘像素也出现了偏移。

5.3.1.1 浑水图像的条纹提取

如图11（a0）～11（a3）所示，随着水体浑浊程度的增加，浑水图像呈现雾状模糊现象，黑白块条纹边缘特性越来越不清晰。通过计算各类图像的平均梯度数据发现，由于水下雾化模糊，图像颗粒感提升，水下条纹图像的平均梯度（Aver⁃age gradient）缓增，图像的平均梯度从2.15增加到2.50。随着浑浊情况的增加，图像二值化结果显示黑白边缘分界逐渐模糊，边缘上噪声增加，边缘特征弱化。从条纹提取结果可以看出，水下条纹提取毛刺增加，边缘扩大，浑水图像边缘提取位置有一定的偏移。对比清水和90 g浑水的条纹提取结果和细节图（图11（d0）和11（d3））可知，清水中黑白条纹边缘像素提取无毛刺，基本符合直线分布；90 g浑水条纹提取细节图像中边缘模糊，条纹边缘出现大量毛刺，甚至出现条纹边缘位置的偏移。

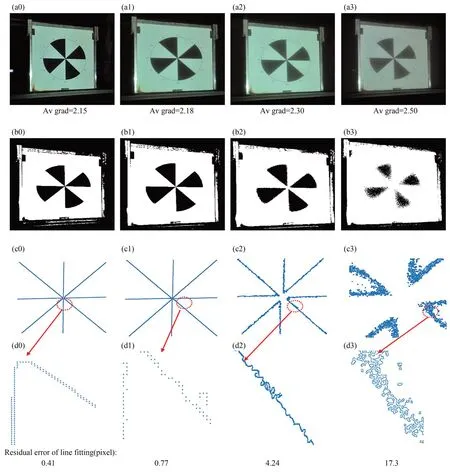
图11 不同水体中的图像和条纹提取结果分析（a0）～（a3）不同水体中采集的图像；（b0）～（b3）不同水体中图像二值化结果；（c0）～（c3）不同水体中图像的条纹提取结果；（d0）～（d3）不同水体中条纹提取细节结果Fig.11 Analysis of image and stripe extraction results in different turbid water（a0）～（a3）Images of different turbid water；（b0）～（b3）Binary images of different turbid water；（c0）～（c3）Stripe extraction in different turbid water；（d0）～（d3）Detail of stripe extraction

根据2.1节水下测量模型可知，当条纹边缘直线垂直于折射平面到水体中平面物体，测量图像中的条纹边缘也应为直线。为了评价条纹边缘像点的提取精度，这里采用条纹边缘上直线拟合残差来衡量。从条纹提取细节结果可以看出水体越浑浊，浑水图像的直线拟合和清水图像的直线拟合偏离越大。清水图像的直线拟合残差为0.41 pixel；随着浑浊程度的增加，浑水图像的直线拟合残差分别为0.77，4.24和27.09 pixel。

从以上数据可以看出，随着水体中泥沙含量的增加，图像质量逐渐退化，条纹提取误差加大。但图像退化质量和条纹提取误差并不随泥沙含量的增加线性恶化。当水体浑浊超出某一数值时，图像质量急剧退化，严重影响条纹提取，造成条纹解码错误，从而引起视觉测量失败。

5.3.1.2 浑水图像的条纹解码

在本文提出的多条纹结构光模型中，一条条纹对应一个测量光平面，条纹的正确解码在结构光测量过程中至关重要。根据条纹编码规则公式（8）可知，采用各个条纹相对于初始条纹的夹角来区分条纹。本文采用单场条纹图中包含4条条纹，通过5场投影测量图获得20条测量条纹。这样，单场条纹间隔角度均匀分布于360°范围内，相邻条纹间最大角度偏移量为45°，相邻条纹间偏移范围选取（-22.5°，22.5°］。每个条纹的解码规则和四种水体的条纹图解码结果如表3所示。当加入90 g泥沙的浑水时，水下图像模糊加剧，条纹提取精度急剧下降，进而引起条纹解码错误。

5.3.2 浑浊水体对三维测量精度影响

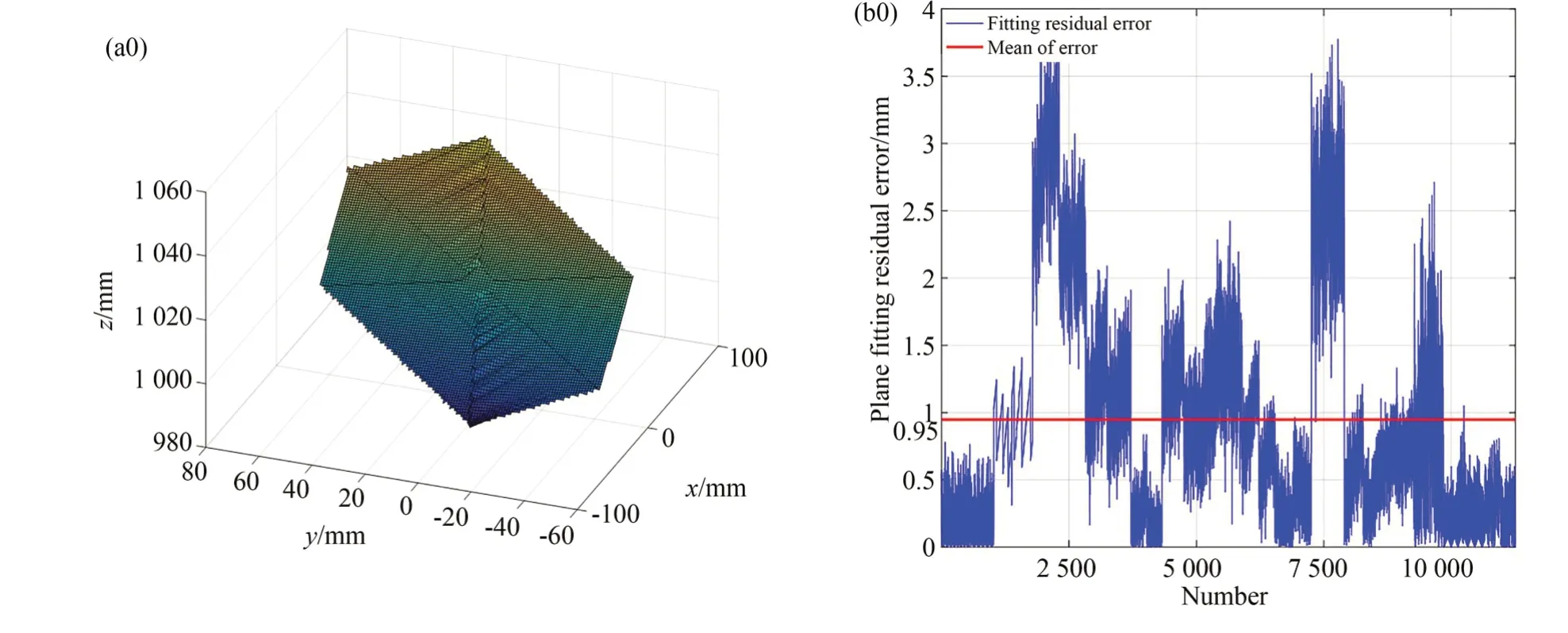
为了分析浑浊水体对三维形貌数据计算影响程度，这里对清水和各类浑水情况下三维测量进行实验分析。从图12（a0）～12（a3））可以看出，随着水体浑浊程度的增加，平面重建结果从光滑平面逐渐变得粗糙；平面拟合残差也逐步加大，清水条件下平面拟合残差为0.95 mm，含有40 g泥沙的浑水下平面拟合残差为1.93 mm，含有60 g泥沙的浑水下平面拟合残差为5.43 mm，含有90 g泥沙的浑水下平面拟合残差为21.43 mm。清水和三种不同浑浊水体中条纹解码结果如表3所示，其中Muddy water1-3分别表示含40，60和90 g泥沙的浑水环境。以第一场条纹解码为例，一场测量图像中包括条纹s1，s6，s11和s16。四条条纹根据各自的编码规则对条纹直线拟合角度进行解码，四条条纹在清水、40和60 g浑水中解码均为正确结果，条纹s1在Muddy wa⁃ter3中测量图中，由于浑水图像模糊引起条纹拟合角度为-24.59°，解码结果出现错误。五场测量图像在清水和三种浑水中的解码过程中，只有在Muddy water3中出现了三次条纹解码错误。当水体浑浊到一定程度引起条纹解码错误时，三维测量误差会急剧增加。

图12 不同浑浊水体中水下平面物体三维形貌测量结果（a0）～（a3）清水和三种浑水中测量表面图；（b0）～（b3）清水和三种浑水中平面拟合残差数据Fig.12 3D results of planar object under different turbid water（a0）～（a3）Measurement surfaces under clear water and three dif⁃ferent turbid water；（b0）～（b3）Results of plane fitting residuals under clear water and three different turbid water

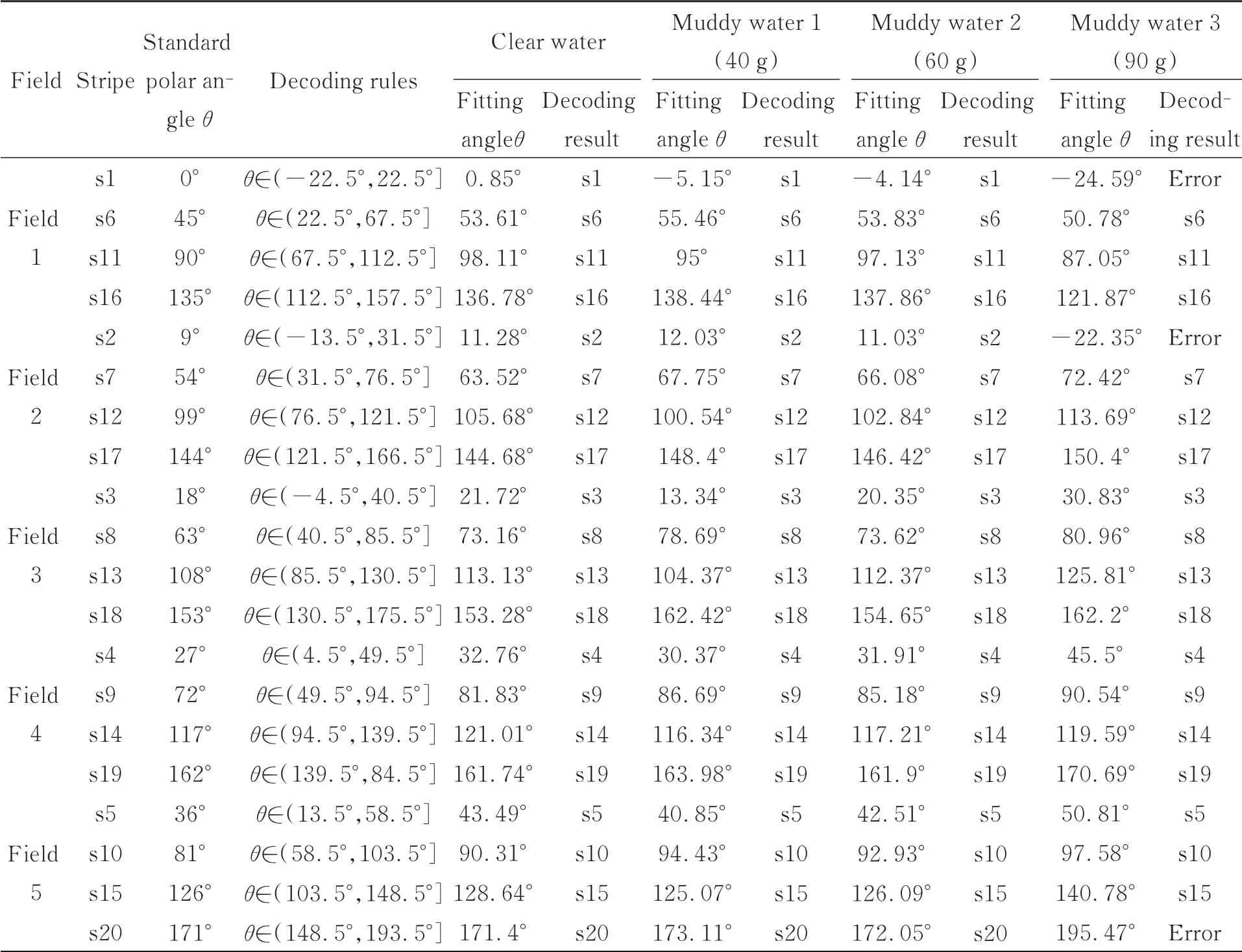
表3 四种水体的条纹解码结果Tab.3 Stripe decoding results of four different water with silt

通过以上实验分析可看出，如表4和图13所示，随着水体浑浊程度的增加，三维测量误差加大（在60 g以内泥沙的情况下，条纹提取误差和三维测量误差随着泥沙量的增加近线性增加）；当水体浑浊到一定程度（泥沙含量到90 g）时，水下图像雾化现象严重带来测量像点提取误差加大和条纹解码错误时，视觉测量精度和相对于测量距离的相对误差急剧下降。

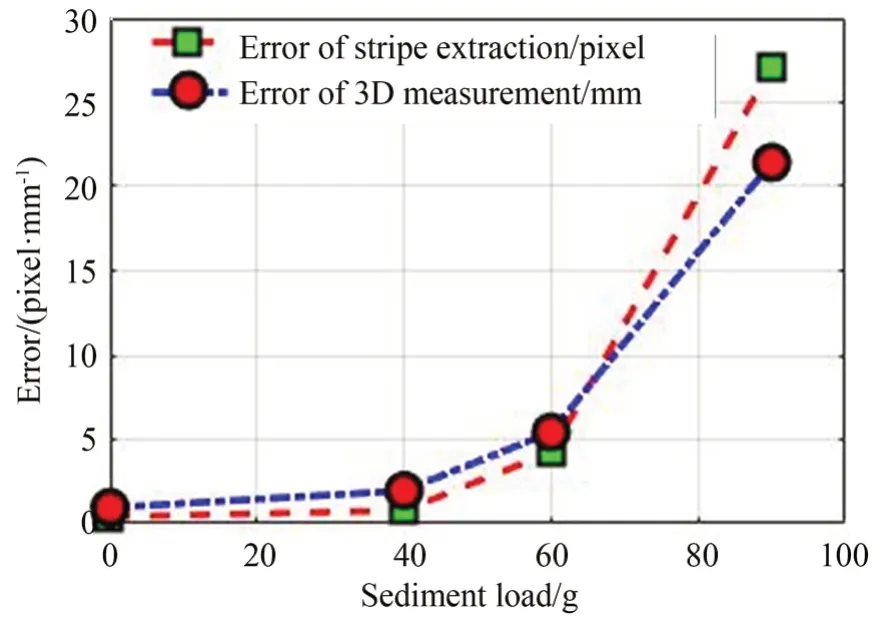
图13 不同浑浊水体的条纹提取误差和视觉测量误差Fig.13 Error of stripe extraction and 3D vision measure⁃ment due to different turbid water

表4 浑浊水体对三维视觉测量的影响Tab.4 Influence of turbid water on 3D vision measure⁃ment

6 结 论

基于视觉的三维形貌测量技术已在工业检测、逆向工程、大型工程形貌缺损探测等方面得到了广泛应用，该技术凭借着高精度、高速、非接触等优点，已成为目前非接触三维形貌测量中的主要方法。

在水下三维测量过程中，由于非线性折射影响以及水下图像退化的问题，使其不利于在实际中的应用。为此，本文从水下测量折射模型和适应退化水下图像特性两方面提出了一种基于多线结构光的水下视觉测量方法。建立了摄像机像平面中二维点与水下被测目标三维点的一一对应关系；分析了浑水条件下像点提取误差和空/水相对折射率扰动对三维点云计算的影响程度；设计了黑白相间的中心旋转结构光条纹，适应了浑水图像降质的情况。实验结果证明，该方法在1 500 mm的测量距离上，清水环境下对瓷瓶自由表面进行测量获得较好的重建效果，对平面获得平面残差为0.95 mm的测量结果；在含有40，60和90 g泥沙的浑水中进行平面三维测量，可以获得平面残差分别为1.93，5.43和21.43 mm的测量结果。