腐蚀拉索钢丝的双蚀坑应力强度因子研究
2021-11-23许红胜任凯颜东煌
许红胜, 任凯, 颜东煌
(长沙理工大学 土木工程学院,湖南 长沙 410114)
1 前言
斜拉索作为斜拉桥主要的承重构件,其运营使用状态相应决定着斜拉桥的运营安全性。斜拉索在长期的运营期中,由于外防护套管破损,原有索体防护体系缺陷等原因,拉索钢丝会出现腐蚀病害,严重影响斜拉索的安全运营寿命。
拉索钢丝腐蚀病害中,点蚀蚀坑参数是与剩余疲劳寿命评估最直接相关的腐蚀病害参数。目前针对拉索钢丝剩余疲劳寿命评估的理论研究,一般采用将点蚀蚀坑简化为单蚀坑裂纹,通过计算裂纹的应力强度因子,利用线弹性断裂力学的方法进行评估。
针对单蚀坑裂纹应力强度因子的计算,国内外学者进行了很多的研究。Daoud等运用有限元法在二维条件下计算了钢筋蚀坑裂纹的应力强度因子并探究了其对裂纹扩展寿命的影响;肖顺等对比分析了J积分、交互积分法、扩展有限元法计算三维裂纹尖端应力强度因子有效性,为复杂结构应力强度因子计算提供了参考;俞树荣等采用三维奇异等参单元建立计算模型,给出了数值模拟模型尺寸及网格大小的取值范围;茹忠亮等通过典型案例分析,得到了将扩展有限元法与水平集法相结合的改进XFEM算法。
工程实际中,点蚀往往是多个蚀坑在相邻位置一起出现,但蚀坑之间的相对位置是不规则的;当蚀坑的应力场之间发生耦合影响时,简单简化为单蚀坑裂纹计算应力强度因子不够准确。针对多裂纹应力场耦合影响的研究,刘钧玉等提出了比例边界有限元计算多裂纹应力强度因子的新算法;马文涛等分析了3个平面应力状态下的多裂纹问题,提出了修正的内部基扩充无网Galerkin法;陈景杰等基于平板模型,提出了基于最大张口位移量确定平行双裂纹尖端应力强度因子的方法。
总的来说,目前针对腐蚀拉索钢丝多点蚀蚀坑分布情况下的应力强度因子的计算,还缺少系统和深入的研究。该文采用数值模拟的方法,研究主、从蚀坑不同位置分布对主蚀坑裂纹应力强度因子的影响,并进一步提出考虑双蚀坑影响的应力强度因子的简化计算方法。
2 单裂纹应力强度因子公式
应力强度因子手册总结了Shak.R.C等研究成果,给出了基于边界积分法的半椭圆表面裂纹应力强度因子的计算公式。一垂直于物体表面的半椭圆形裂纹,垂直于裂纹表面作用有均匀拉伸应力p,裂纹前缘各点的应力强度因子计算公式为:
(1)
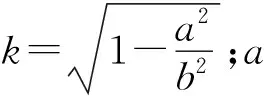
由式(1)可知:KΙmax在椭圆短半轴,对含裂纹构件的起裂和断裂起着极为重要的控制作用。其中:
(2)
3 计算模型的确定
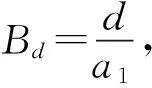
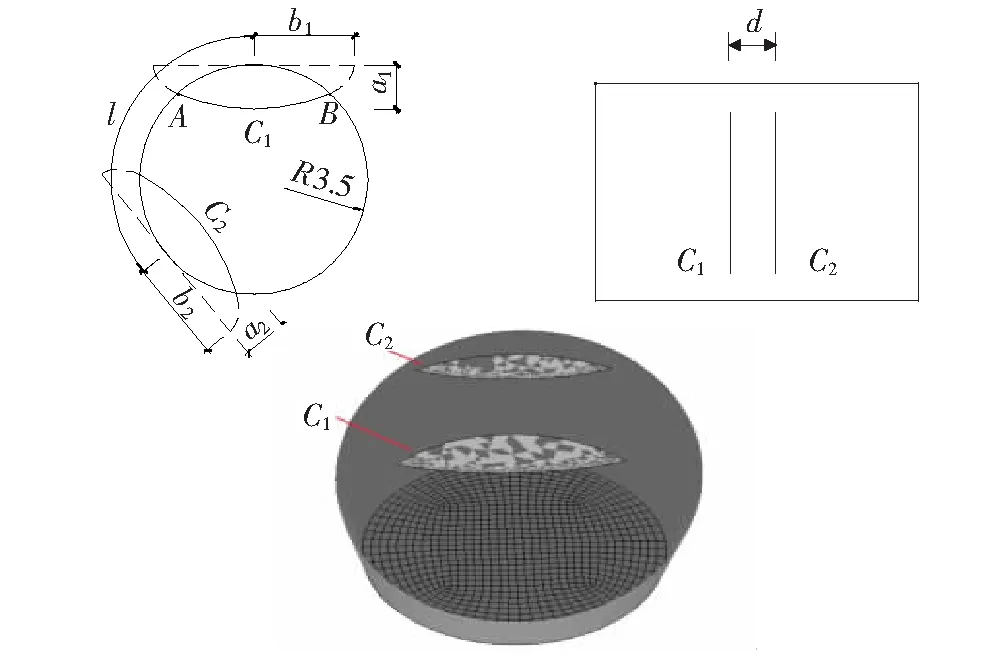
图1 含两条裂纹的钢丝模型
有限元分析软件采用Franc 3D和Abaqus相结合。对模型划分网格时,沿轴向单元尺寸为0.5 mm,圆截面布置尺寸分别为0.3 mm和0.2 mm,裂纹前端划分单元尺寸为0.05 mm,荷载大小采用650 MPa,边界条件约束轴向转动,固定X、Y方向位移。
4 影响系数的计算与分析
为了验证数值模拟的准确性,将数值计算与理论计算的结果进行比较分析。按照设计尺寸对单裂纹模型进行设置后施加荷载进行计算,计算结果如图2所示,KΙmax=1 479.28 MPa·mm1/2。按照式(2)进行积分计算,查得参数M=1.14,理论值KΙmax=1 457.29 MPa·mm1/2。数值计算与理论值误差为1.4%,由此可知数值模拟计算结果可靠。
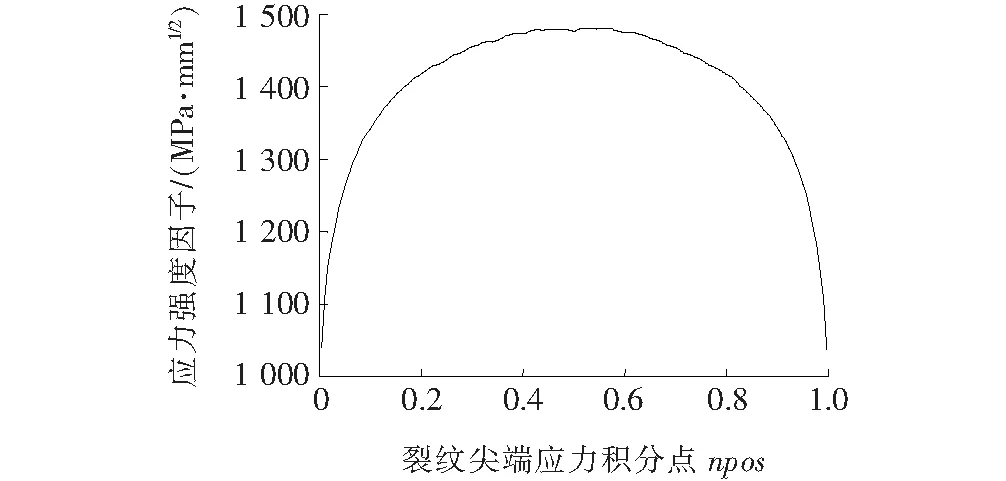
图2 单裂纹数值计算结果
4.1 轴向距离的影响
为了研究轴向距离的影响,需控制周向间距不变,进而通过改变Bd、Ba的大小来探究f的变化情况。该文设置Bd变化范围为0.2~6.0,即轴向间距为裂纹深度的0.2~6.0倍,Ba的变化范围为0.2~1.0即从裂纹大小为主裂纹的0.2~1.0倍。由于计算数据过多,该文只列举部分数据,如图3所示。
陈龙国[37]认为,书法作为祖国传统艺术的瑰宝,光是繁琐考据是不能满足人民群众日益提高的审美要求的。随着时间的推移,碑学与帖学便逐渐倾向于对书法范本的美学探讨,形成了以不同审美观相对峙的学术流派,使碑与帖在概念上发生了质的变化。
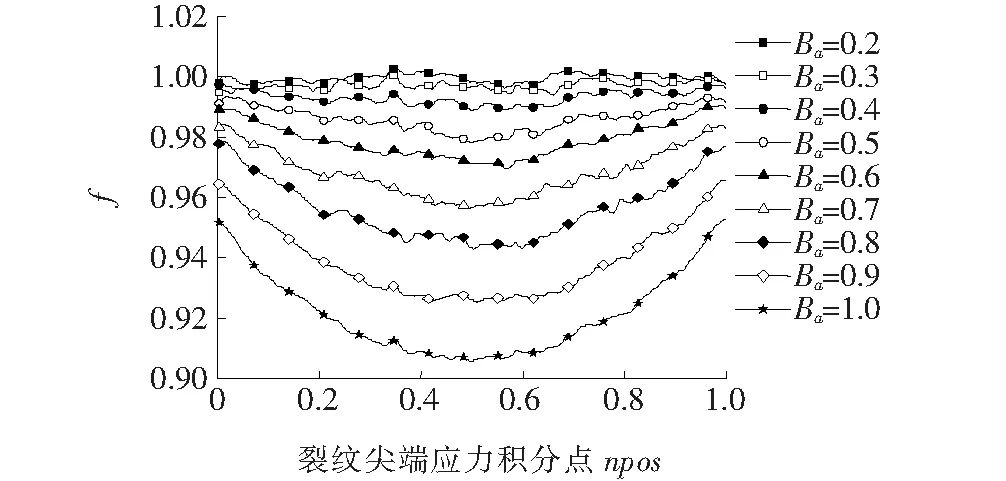
图3 Bd=2裂纹尖端各点f值
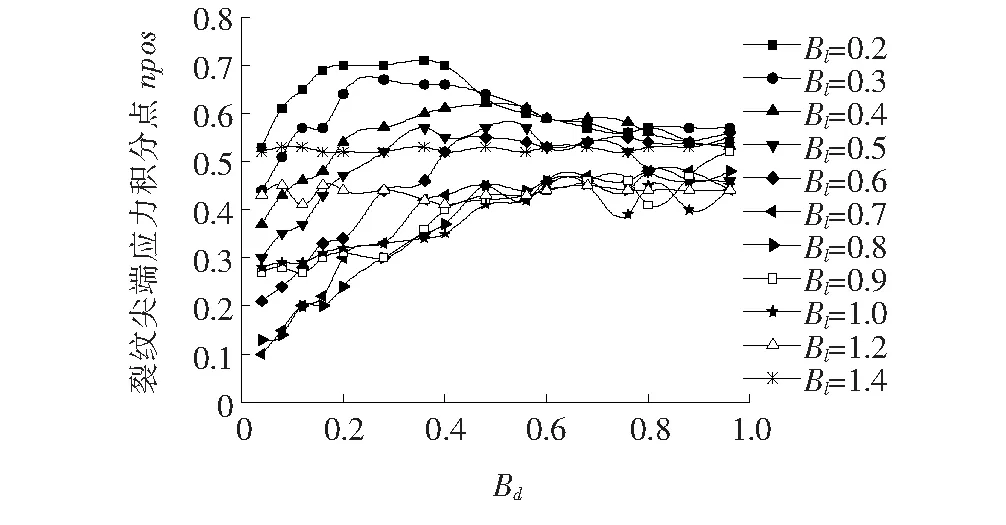
由图3可知:不论Bd、Ba如何变化,共线双裂纹的f值基本小于等于1.0,即在共线情况下从裂纹的存在,降低了主裂纹裂尖的应力强度因子值,每条裂纹裂尖的f值大致为规则的曲线形状。用尖端最深点代表每条曲线,将不同裂纹比绘制成关于轴向间距比的曲线,如图4所示。由图4可知,当0.4≤Ba≤0.9时,随着Bd的增加,f值的变化趋势大概呈现先减少后增加的情况,而且Ba越大其曲线极小值点对应的横坐标越小,即从裂纹越大,其对主裂纹产生的影响减小的相对轴向间距越小,但影响程度还是随着从裂纹的增大而增大;当0.2≤Ba≤0.4时,f值不随轴向距离的变化而变化;而Ba=1.0时的f值则从开始的0.72呈现出逐渐增加的趋势。该文在文献[16]的基础上,规定当0.98 图4 Ba-Bd曲线 由于共线双裂纹之间应力强度因子相互削弱,工程实际中可按单蚀坑裂纹计算,结果偏于安全,该文仅对影响趋势做描述,相互影响系数拟合不做赘述。 研究周向距离l对f的影响,设定不同的从裂纹大小在一定的轴向距离比条件下(Bd=0.2,0.4,…,4.4,4.8),改变Bl的大小,计算对应的f值。设置Bl变化范围为0.2,0.3,…,1.2,1.4共11组,按照周向距离比换算成主从裂纹中心与钢丝圆心所形成的角度,实现从裂纹在模型中的定位,其中Bl=0.7为90°,Bl=1.4为180°,按照逆时针分布。 4.2.1 等长裂纹的影响 控制从裂纹与主裂纹大小一致,在不同的轴向距离下改变周向距离的大小,计算出每条裂纹裂尖的应力强度因子值,进而求出其f值。将同周向距离,不同轴向距离裂纹的f值绘制在同一图上,共得11组数据,一组数据图如图5所示。 由图5可知,无论两裂纹周向距离Bl(中心夹角)如何变化,与f=1.0轴交点左右侧,各曲线大致按照顺序依次排列,即从裂纹对主裂纹的增强或削弱效应都随轴向距离的增加而逐渐减小,但Bd≥4(轴向距离不小于4倍主裂纹深度)的曲线均为f=1.0附近的平直线,即两裂纹之间互不影响。当Bl<0.7时,各曲线与f=1.0轴的交点随着周向距离的增加逐渐向A点靠拢,交点左边f<1.0,表现为削弱影响,交点右边f>1.0,表现为加强作用;当0.7≤Bl≤1.4时,各曲线与f=1.0轴交点由B点附近向A点移动,交点左边f>1.0,表现为加强作用,交点右边f<1.0,表现为削弱影响;最终当两裂纹为对侧分布(Bl=1.4)时,各曲线与f=1.0轴再无交点,不再存在增强效果。 图5 Bl=0.6裂纹尖端f图 以裂纹尖端节点为横坐标,f为纵坐标,在Bd相同的情况下,绘制出不同周向间距的裂纹曲线,部分结果如图6所示。 由图6可知:当0.2≤Bl<0.6时,曲线都与f=1.0轴有一个交点,交点左侧(靠近A点)f<1.0,随着轴向距离的增加f值逐渐增加,从裂纹对主裂纹的削弱作用逐渐减小;交点右侧f>1.0,且随着轴向距离的增加f值逐渐减小,从裂纹对主裂纹的增强作用逐渐减小。随着Bl的增加,交点逐渐左移,大致与两条裂纹重合点位置接近,即随着两裂纹中心夹角的增加,裂纹投影面重合位置越来越靠近A点,重合区域f<1.0,重合区域外f>1.0;当0.7≤Bl<1.4时,即两条裂纹中心夹角大于等于90°时,曲线与f=1轴的交点从B点附近开始,逐渐向A点移动,将C2按照C1与圆心的对称轴对称到C2的位置后,交点与B点的距离大致等于C1与C2投影区域长度,且重合区域f<1.0,重合区域外f>1.0;当Bl=1.4时,各条曲线大致相互平行,与f=1.0轴不再有交点,0.2≤Bd≤3时,从裂纹对主裂纹存在削弱现象,且随着Bd的增加,削弱现象逐渐减弱。 图6 不同Bd时,周向距离影响下f值曲线 4.2.2 不等长裂纹的影响 结合轴向距离影响一节计算数据分析,从裂纹对主裂纹的影响随着从裂纹的增大而增大。该节考虑不等比从裂纹的影响,除从裂纹尺寸外,其他均与等比裂纹尺寸相同。分别以Ba=0.2、0.5、0.8为例,计算了不同状态下裂尖应力强度因子变化情况。如图7所示为Bd=0.4情况下,裂尖应力强度因子相对单裂纹应力强度因子变化情况。 图7 Bl=0.5,Bd=0.4裂纹尖端f图 观察可知:对于同一Bl,随着从裂纹尺寸的增加,其对主裂纹的影响也逐渐增大,fmax也逐渐增大。当从裂纹尺寸足够小时,其对主裂纹的影响可以忽略。由此可知,当存在从裂纹比主裂纹小时,其对主裂纹的影响可按同等大小的从裂纹来计算,且结果偏安全。 对于含有双裂纹的构件最大应力强度因子需要考虑裂纹间的相互影响,而且裂纹之间的相互影响使得主裂纹裂尖的应力强度因子曲线形状不规则,导致整条裂纹的K值计算较为复杂。在工程计算中主要考虑裂尖最大应力强度因子值,因此,为简化计算,该文提出以下计算思路: (1)按照单蚀坑裂纹计算KΙmax。 (2)考虑裂纹间相互影响,规定双裂纹与单裂纹裂尖最大应力强度因子比值为修正系数f′: f′=KΙmax双/KΙmax单 (3) (3)对式(2)进行修正为: (4) (4)计算KΙmax对应点的位置。 按照上述步骤可以算出从裂纹作用下,主裂纹尖端最大应力强度因子值及其位置。 为了计算N值,用每条裂纹尖端KΙmax值代表一条裂纹,绘制出Bl-Bd曲线,如图8所示。 图8 Bl-Bd曲线 由图8可知:对于0.8 表1 修正系数公式参数 f′=D1x+D2x2+D3x3+D4x4+C (5) 用数据处理软件Origin进行曲线拟合,同时控制其相关系数在合理范围内,相关系数越大则拟合效果越好,各拟合曲线相关系数分别为:R0.2=0.998 65、R0.3=0.994 7、R0.4=0.991 89、R0.5=0.987 14、R0.6=0.978 04、R0.7=0.977 31、R0.8=0.974 66。可见拟合效果良好。 将每个裂纹KΙmax值所对应的横坐标绘制成关于Bd的曲线,如图9所示,对于0.2≤Bl≤0.7,曲线大致先增加后减少,但减少的趋势随着Bl的增加逐渐减缓;对于0.8≤Bl≤1.0,曲线呈逐渐递增趋势,而Bl=1.2、1.4曲线则基本呈水平直线,其值分别为0.43,0.52(A点为0,B点为1)。将曲线数据进行相关性拟合,得到KΙmax点在裂尖的位置式(6),参数见表2。各拟合曲线相关系数分别为:R0.2=0.964 26、R0.3=0.962 87、R0.4=0.982 95、R0.5=0.970 21、R0.6=0.986 67、R0.7=0.982 37、R0.8=0.984 43、R0.9=0.952 23、R1.0=0.971 1。可见拟合效果良好。 表2 KΙmax位置公式参数 图9 KΙmax位置曲线 L=E1x+E2+E3+E4+E5+G (6) (1)对于共线双蚀坑(l=0),Ba≤0.4时,从裂纹对主裂纹应力强度因子无影响;当0.4 (2)对于不共线双蚀坑(l≠0),两裂纹相交区域内应力强度因子减小,相交区域外增大;当Bl一定时,随着轴向间距的增大,裂纹间的相互影响逐渐减弱;当Bd≥3.8时,可忽略从裂纹对主裂纹应力强度因子的影响;随着从裂纹尺寸的增加,不论周向间距如何变化,其对主裂纹应力强度因子的影响都随着裂纹尺寸的增加而增加。 (3)拟合出0.2≤Bl≤0.8时,双蚀坑裂纹尖端KΙmax双修正系数f′与轴向间距的关系式,且拟合程度良好;0.8 (4)拟合出0.2≤Bl≤1.0时,KΙmax双最大值点的位置曲线,拟合效果良好;给出了双蚀坑裂纹应力强度因子计算思路。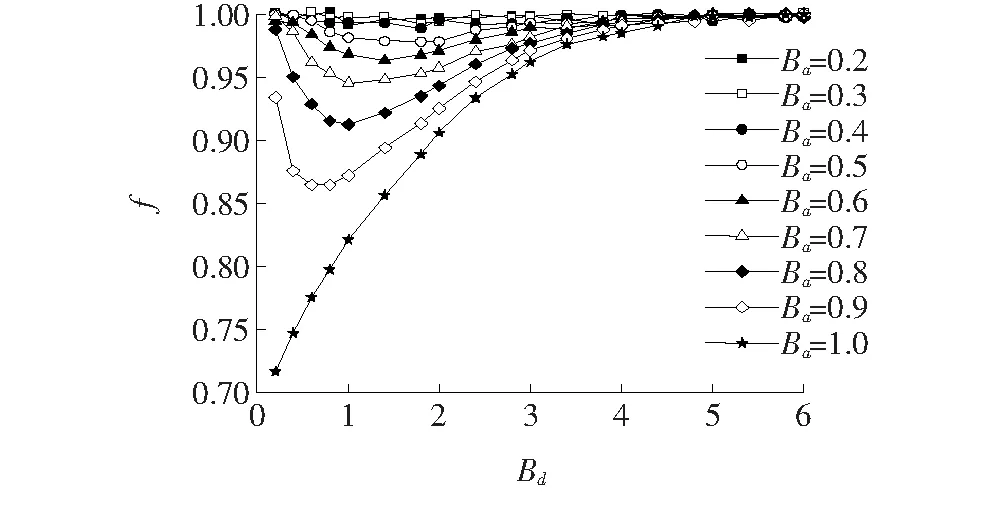
4.2 周向距离的影响
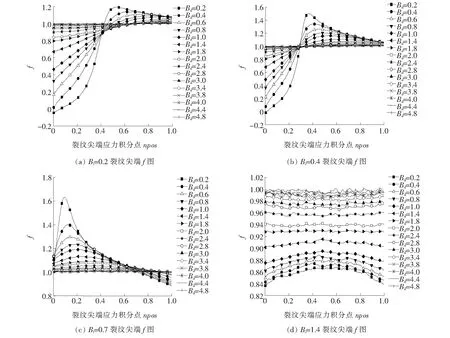
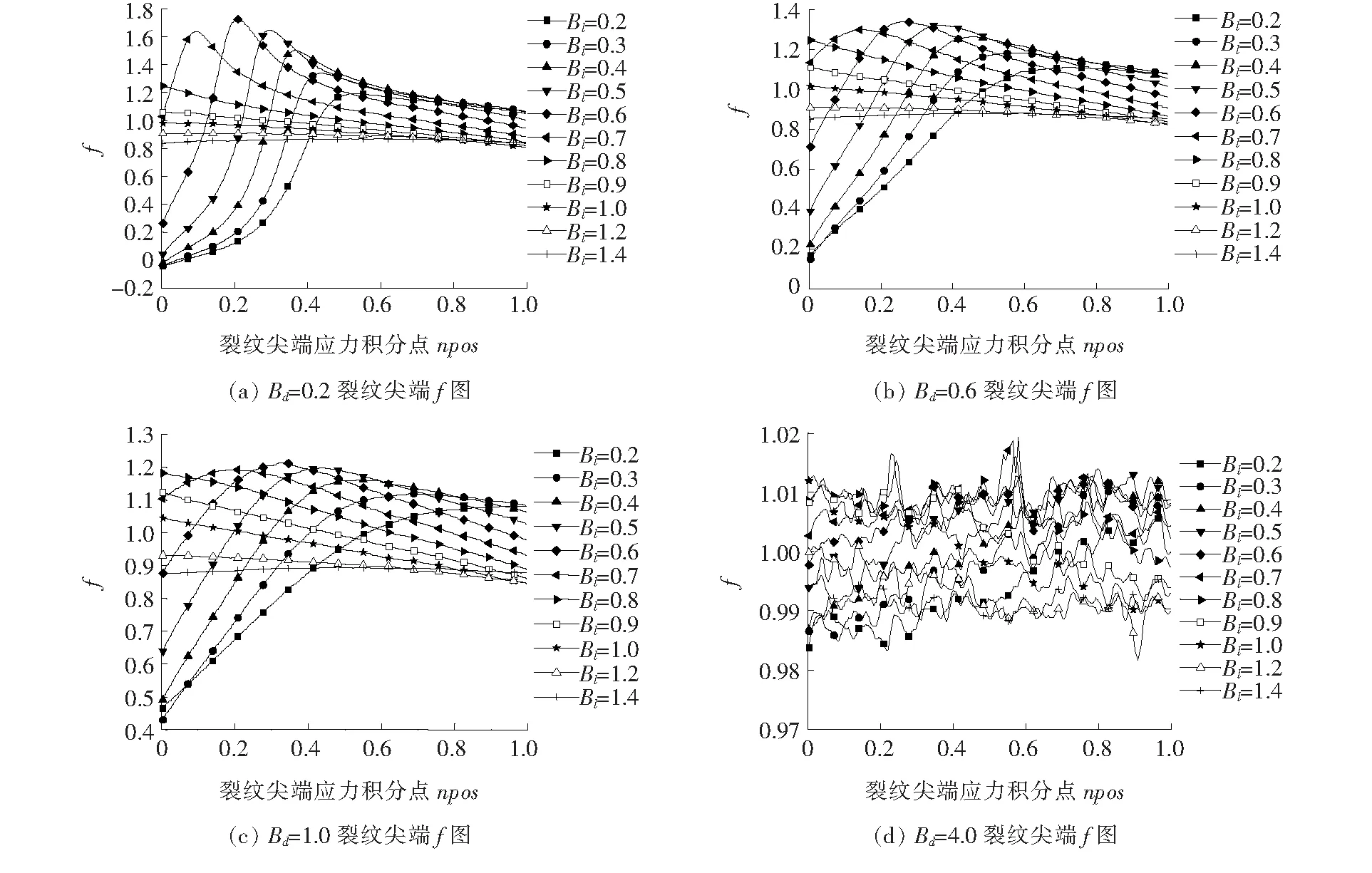
5 双裂纹应力强度因子简化算法
6 结论
