抓住典型例题,深化问题研究
2021-11-23文/蒋飞
文/蒋 飞
平均数、中位数和众数都反映了一组数据的集中趋势,但在实际问题中,我们该如何选用平均数、中位数和众数呢?下面,我们将一起围绕教材例题,开展相关问题的探究。
一、例题呈现,抓住本质
例1 某公司职工的月工资情况如下:
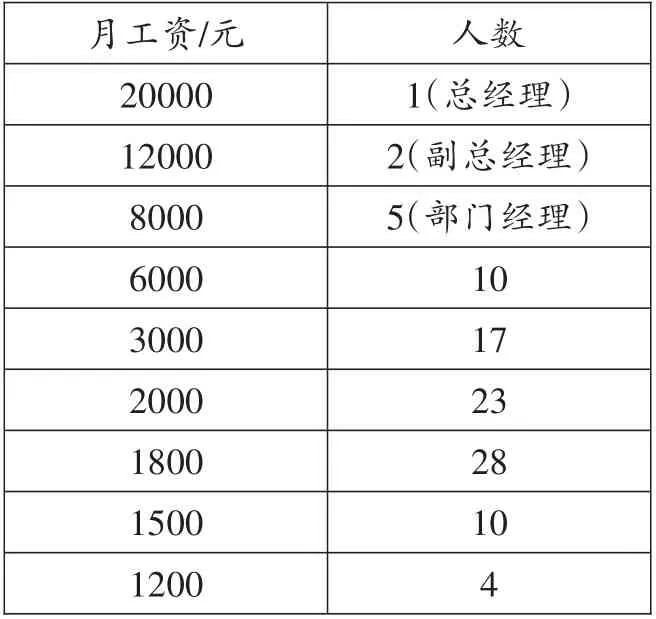
____________________________人数______________________1(总经理)_____________________2(副总经理)_____________________5(部门经理)______________________________10 17______________________________23_______________________________28_______________________________10________________________________4月工资/元______________________20000_______________________12000_______________________8000________________________6000________________________3000 2000________________________1800_________________________1500_________________________1200________________________
根据上表,可以算得该公司职工月工资的平均数、中位数和众数分别为3112 元、2000 元、1800 元。如果你是该公司的一员,那么会更加关注其中的哪一个数据呢?
【分析】这是一道开放性问题,解决此类问题需要同学们理解以下两点。(1)平均数、中位数和众数是度量一组数据集中趋势的3个统计量,它们具有各自的特点,有助于我们从不同的角度描述一组数据的集中趋势。计算平均数时,所有的数据都参与运算,能较充分地利用数据所提供的信息,反映一组数据的平均水平,但是易受一组数据中极端值的影响;中位数是一组数据按大小顺序排列后中间位置的代表值,它不受异常值影响,但是不能充分利用数据的信息;众数是一组数据中出现次数最多的数据,往往是人们尤为关心的统计量,但它不具有唯一性。(2)在实际应用中,用哪一个统计量来描述数据的集中趋势,需要根据数据的特征和问题的具体情况做出恰当的选择。
二、变式拓展,深入探究
例2 某公司月工资情况如下:
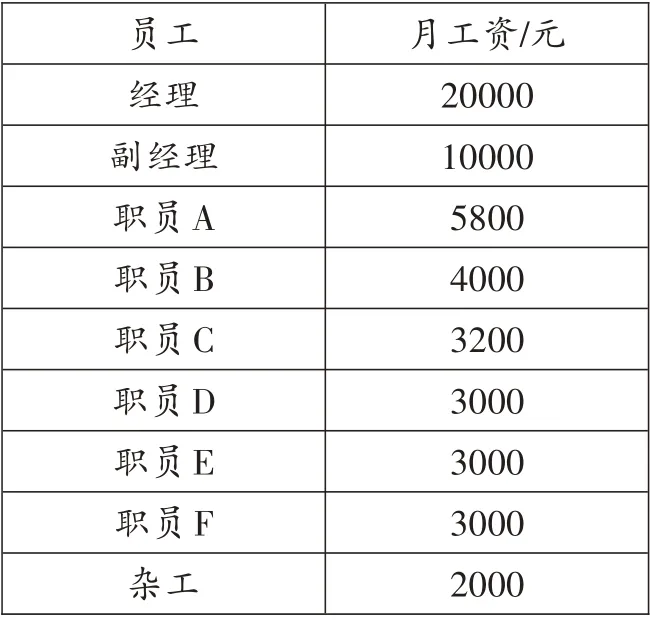
___________________________员工_____________________________经理______副经理___________________________职员A____________________________职员B____________________________职员C___________________________职员D___________________________职员E___________________________职员F_____________________________杂工月工资/元____20000______10000______5800_______4000_______3200_______3000_______3000_______3000_______2000_______
该公司三位职员对收入情况作出如下评价。
甲:我的月工资是3200 元,在公司中算中等收入;
乙:我们好几个人的月工资都是3000元;
丙:我们公司员工收入很高,月工资为6000元。
请你用所学知识回答下列问题:
(1)甲所说的数据3200 元,我们称之为该组数据的________;(填平均数、众数或中位数)
(2)乙所说的数据3000 元,我们称之为该组数据的________;(填平均数、众数或中位数)
(3)丙是用什么方法得出6000元的?
(4)甲、乙、丙三人的说法中,谁的说法可以较好地反映该公司职员收入的一般水平。
【分析】本题主要考查平均数、中位数、众数的意义,需根据实际情况分析得出答案。
解:(1)甲所说的数据3200 元,我们称之为该组数据的中位数。
(2)乙所说的数据3000 元,我们称之为该组数据的众数。
(3)由(20000+10000+5800+4000+3200+3000×3+2000)÷9=6000(元),可知,丙是用计算平均数的方法得出6000元的。
(4)因为平均数受到了这组数据中极端值的影响(经理、副经理月工资),所以不能反映该公司职员收入的一般水平。根据中位数和众数的意义可得:甲、乙两人的说法能较好地反映公司员工收入的一般水平。
三、中考链接,总结提升
例3 (2019·浙江温州)车间有20 名工人,某一天他们生产的零件个数统计如下表:
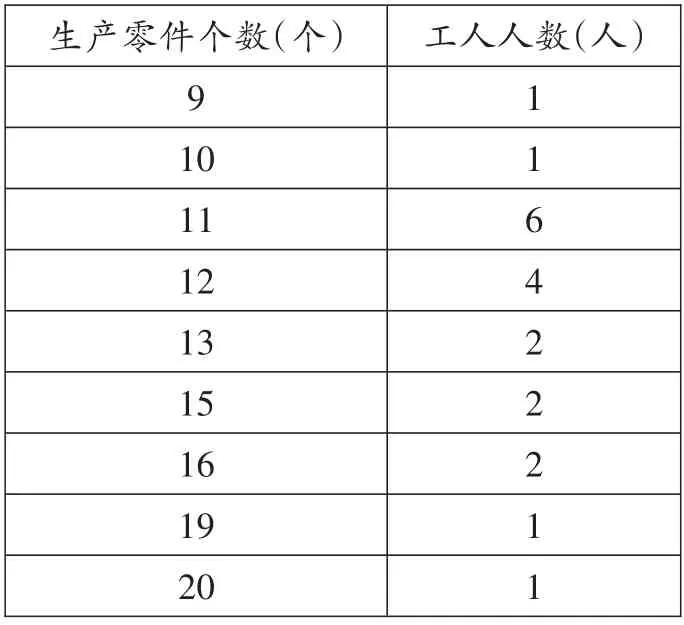
__生产零件个数(_______个)_____________________________________9_____________________________________10_____________________________________11 12___________________________________13___________________________________15___________________________________16___________________________________19____________________________________20工人人数(人)1_______1_______6_______4 2_______2_______2_______1_______1_______
(1)求这一天20 名工人生产零件的平均个数。
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施。如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
【分析】(1)根据平均数的计算方法进行计算即可;(2)求出中位数、众数、平均数,从大多数员工能够完成任务来确定“定额”。

答:这一天20 名工人生产零件的平均个数为13个。
(2)中位数为12个,众数为11个。当定额为13 个时,有8 人达标,6 人获奖,不利于提高工人的积极性;当定额为12 个时,有12 人达标,8 人获奖,不利于提高大多数工人的积极性;当定额为11 个时,有18 人达标,12 人获奖,有利于提高大多数工人的积极性。因此,定额为11 个时,有利于提高大多数工人的积极性。
通过以上探究,我们深知,只有熟知平均数、中位数、众数的概念及意义,才能在解决实际问题时根据具体情况做出适合的选择。
(作者单位:江苏省常州市武进区湖塘实验中学)
挑 战 压 轴 题
为了防控新冠疫情,某地区积极推广疫苗接种工作,卫生防疫部门对该地区八周以来的相关数据进行收集整理,绘制得到图表如下:
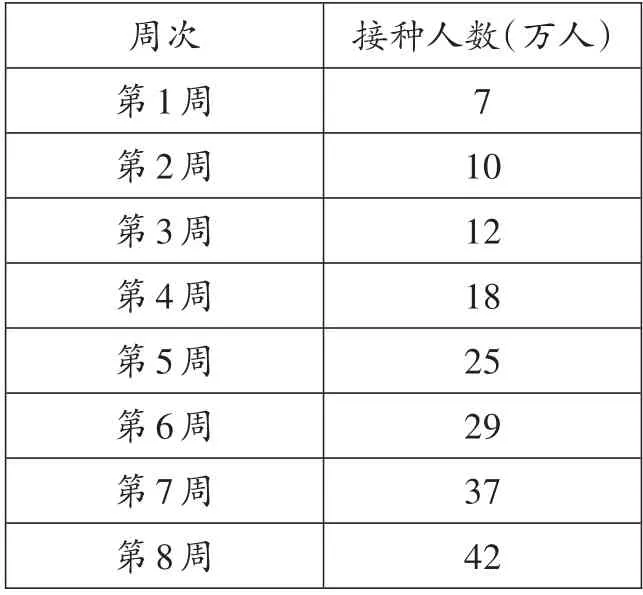
该地区每周接种疫苗人数统计表
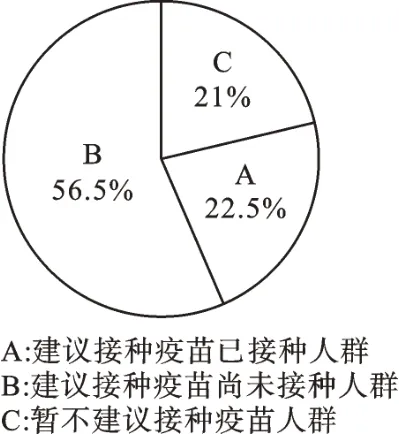
该地区全民接种疫苗情况扇形统计图
根据统计表中的数据,建立以周次为横坐标,接种人数为纵坐标的平面直角坐标系,并根据以上统计表中的数据描出对应的点,发现从第3 周开始这些点大致分布在一条直线附近,现过其中两点(3,12)、(8,42)作一条直线(如图所示,该直线的函数表达式为y=6x-6),那么这条直线可近似反映该地区接种人数的变化趋势。
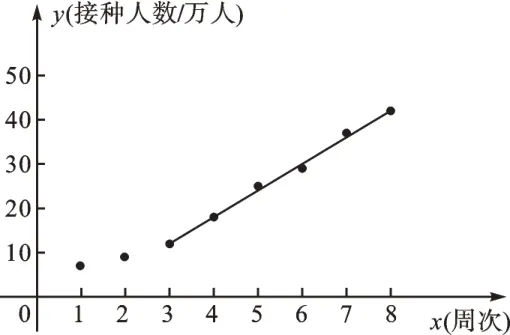
请根据以上信息,解答下列问题:
(1)这8 周中每周接种人数的平均数为____万人;该地区的总人口约为____万人。
(2)若从第9 周开始,每周的接种人数仍符合上述变化趋势。
①估计第9 周的接种人数约为____万人;
②专家表示,疫苗接种率至少达60%,才能实现全民免疫。那么,从推广疫苗接种工作开始,最早到第几周,该地区可达到全民免疫的标准?
