混合式磁流变弹性体隔振器多目标优化设计
2021-11-22杜永飞
范 伟, 孟 江, 杜永飞, 刘 凯, 蒋 童
(中北大学机械工程学院, 太原 031051)
在振动控制领域,利用磁流变弹性体(magnetorheological elastomer,MRE)的磁控制特性设计具有可调整刚度的隔振装置成为研究热点[1]。
现阶段座椅隔振系统中,被动隔振仍占据大部分市场,但其宽频隔振效果不佳[2]。磁流变弹性体隔振器因刚度可调,可在更宽频域情况下对隔振系统进行实时调节,但由于磁流变弹性体隔振器需要接入外界能量,能耗将会升高,因此对隔振器功率的降低显得格外重要。
针对结构优化问题,赵灿等[3]计算分析了磁流变弹性体阻尼器典型磁路但磁流变弹性体未能率先饱和;胡志坚等[4]分析了磁路饱和情况并进行优化计算;刘旭辉等[5]采用多目标遗传算法在磁流变阻尼器降低功耗与减小体积间寻得平衡;Parlak等[6]以阻尼力和最大磁通量为目标函数优化了磁流变液阻尼器;Dong等[7]采用NSGA-Ⅲ算法以阻尼力与动态范围和响应时间对几何尺寸进行优化,显著改善磁流变阻尼器间隙内磁流变密度均匀性;彭虎等[8]采用MOGA多目标优化算法对磁流变阻尼器(MRD)阻尼力与可调倍数进行优化,有效提高了阻尼缝隙处磁场强度;郑玲等[9]针对磁流变液阻尼器活塞体积和功率消耗采用加权的方式整合至单目标函数进行优化,加权值不宜选取且结果误差较大。
为了在现有混合式磁流变弹性体隔振器[10]低功率和大磁致刚度之间寻求平衡,现以汽车座椅为隔振对象,针对混合式MRE隔振器的磁路模型和关键零件的几何尺寸,采用遗传算法进行多目标优化方法,寻求在特定要求情况下的结构参数最优解。以期为后续结构设计及实测提供理论和实验依据。
1 磁流变弹性体隔振器的工作原理
隔振器具体结构由图1所示。线圈会在通电时产生环形磁场,同时作用于剪切和压缩MRE。通过调节线圈中的励磁电流,调节磁场,进而调节磁流变弹性模量和隔振器的磁致刚度,隔振系统的固有频率发生变化,从而避开外界激励的频率,令隔振对象的振动减小[11]。
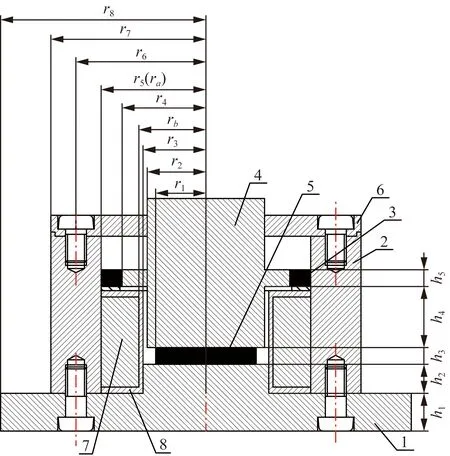
1为底座;2为导磁套筒;3为剪切MRE;4为动导磁块;5为压缩MRE;6为端盖;7为线圈;8为线圈龙骨;r1为压缩MRE半径;r2为动导磁块底部半径;r3为线圈龙骨内半径;rb为线圈内半径;r4为剪切MRE内半径;r5(ra)为剪切MRE外半径(线圈外半径);r6为螺栓孔位置半径;r7为导磁套筒外半径;r8为底座外半径;h1、h2为底座厚度;h3为压缩MRE厚度;h4为动导磁块底部厚度;h5为剪切MRE厚度图1 混合式MRE隔振器结构Fig.1 Structure of hybrid MRE isolator
如图1所示半径尺寸设计为变量约束的形式,即通过确定尺寸r3,对其他尺寸采用加减变量的方式进行约束,如表1所示。表1中Δi-j为两半径之间的差值,主要对半径起到约束作用,仅需对其中的差值约束变量进行优化即可。半径变量及高度初始尺寸数值如表2所示。

表1 半径尺寸关系Table 1 Radius dimension relationship
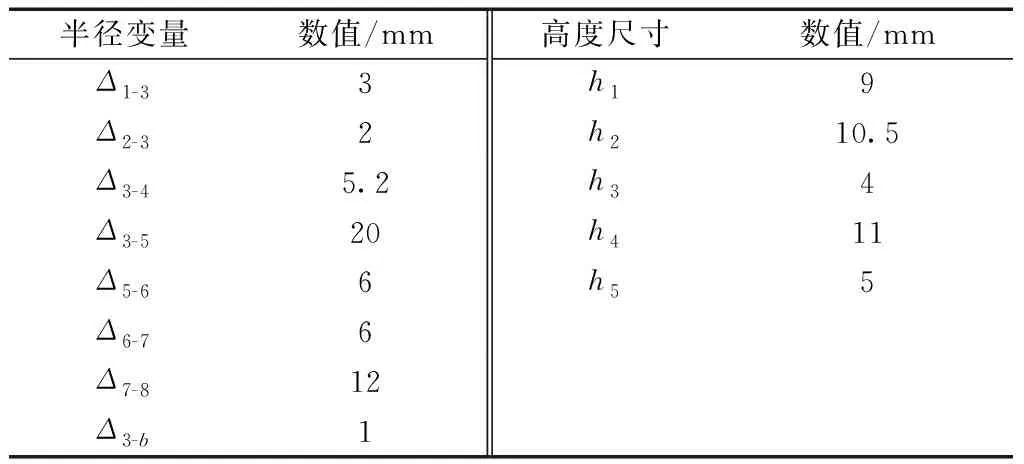
表2 半径变量及高度初始尺寸Table 2 Radius variable and height initial dimension
2 混合式磁流变弹性体隔振器计算模型
2.1 路性能模型
磁阻类似于电路中的电阻,用Rm表示。隔振器结构的等效磁路如图2所示,表达式[12]如下。
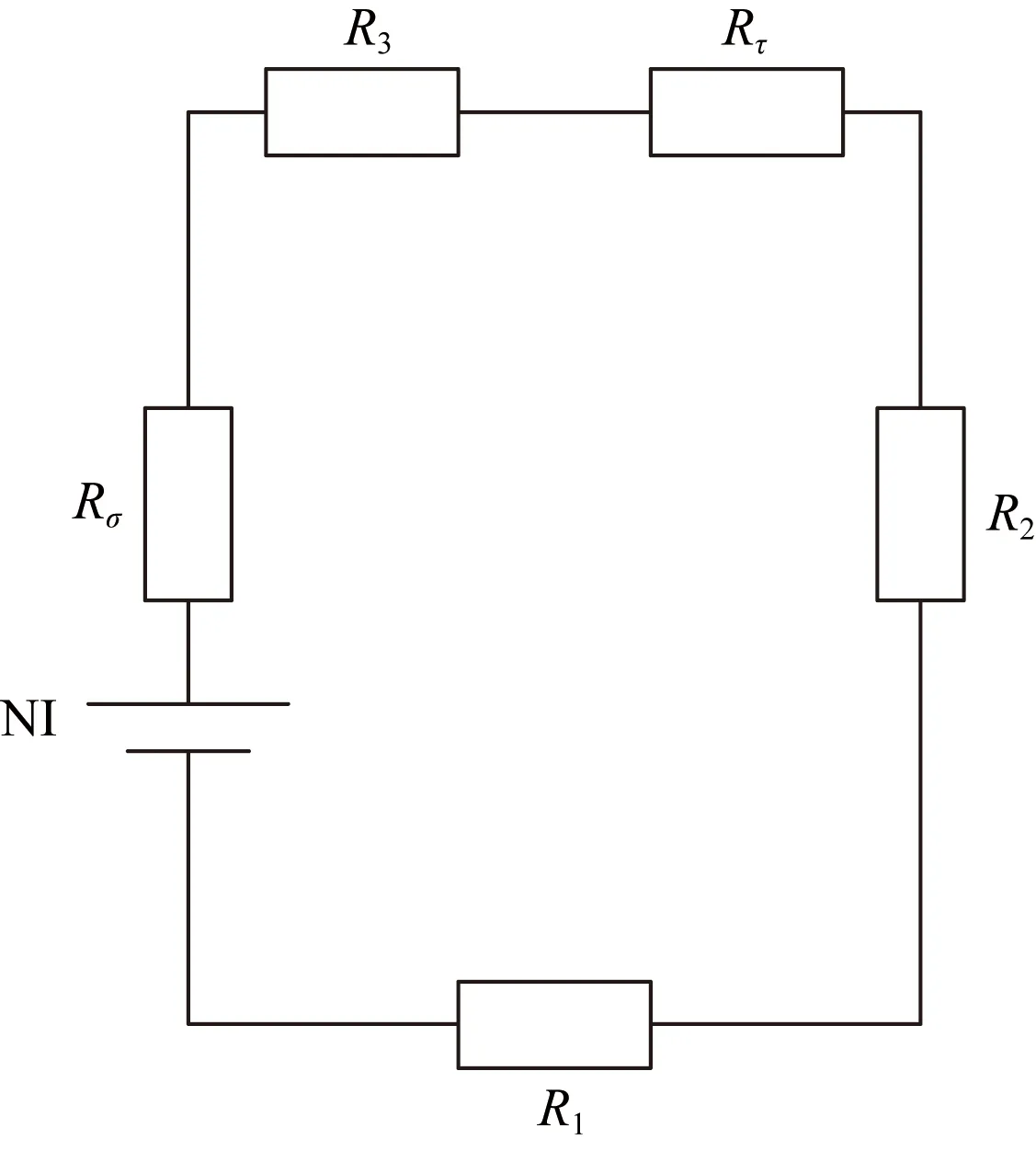
R1、R2、Rτ、R3、Rσ分别为底座、导磁套筒、剪切MRE、动导磁块及压缩MRE对应的磁阻;NI为线圈产生的磁动势图2 等效磁路Fig.2 Equivalent mgnetic circuit
等效磁路磁阻为
Rm=R1+R2+Rτ+R3+Rσ
(1)
底座:
(2)
导磁套筒:
(3)
剪切MRE:
(4)
动导磁块:
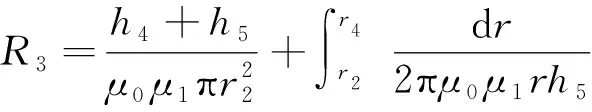
(5)
压缩MRE:
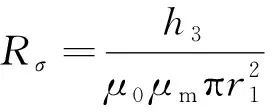
(6)
式中:μ0、μ1、μm分别为真空、碳钢和MRE的相对磁导率,H/m。
由磁路欧姆定律,可得隔振器线圈匝数为
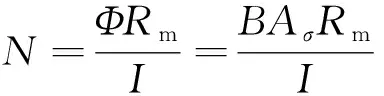
(7)
式(7)中:Φ为穿过压缩MRE的磁通量,Wb;B为压缩MRE处的磁感应强度,T;Aσ为压缩MRE的截面积,m2;Rm为等效磁路磁阻,H;I为线圈通过的电流,A。
由于MRE材料的磁饱和强度约为0.7 T[10],要求压缩MRE处的磁感应强度为0.7 T,则可将压缩MRE相关参数作为求解的参数进行代入。由图1中的尺寸信息求得压缩MRE的面积Aσ,设线圈通过I= 2 A电流,可在压缩MRE处产生0.7 T的磁感应强度,最终可求得线圈匝数。
2.2 磁致刚度模型
其结构为剪切和压缩混合式MRE隔振器,所以隔振器的总磁致刚度由剪切磁致刚度及压缩磁致刚度组成。
磁致总刚度表达式为
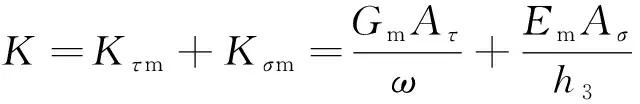
(8)
式(8)中:Kτm、Kσm为剪切磁致刚度、压缩磁致刚度,N/m;Gm、Em为MRE的磁致剪切模量、磁致压缩模量,MPa;Aτ、Aσ为MRE剪切面积、压缩面积,m2;ω为颗粒链长(近似等于MRE径向厚度);对应表达式分别为
(9)
(10)
ω=r5-r4
(11)
Gm、Em由实验测量数据进行拟合[10]得
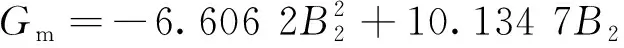
(12)
(13)
根据此路欧姆定律定律可得
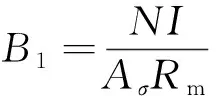
(14)
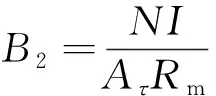
(15)
2.3 功率模型
由式(7)可以求得线圈匝数,则线圈的功率P的计算公式为
P=I2R
(16)
式(16)中:R为线圈的电阻,Ω。
(17)
L=πN(ra-rb)
(18)
式中:ρ为导线电导率, Ω/m;d为导线直径,mm;L为线圈绕线长度,mm;ra、rb分别为线圈的内径和外径,mm。
3 优化设计与分析
为使隔振器功率最低、输出磁致刚度最大,主要从两方面进行尺寸优化,减小磁阻和增加MRE产生的磁致刚度。针对导磁块尺寸、底座部分尺寸、剪切MRE尺寸和压缩MRE尺寸进行优化设计。
3.1 压缩MRE所处线圈内部区域不同位置的磁感应强度
为确定压缩MRE所处轴向位置,分别对MRE所处如图3所示三个位置时,线圈内部区域的磁感应强度进行仿真。得出相应曲线图如图4所示。
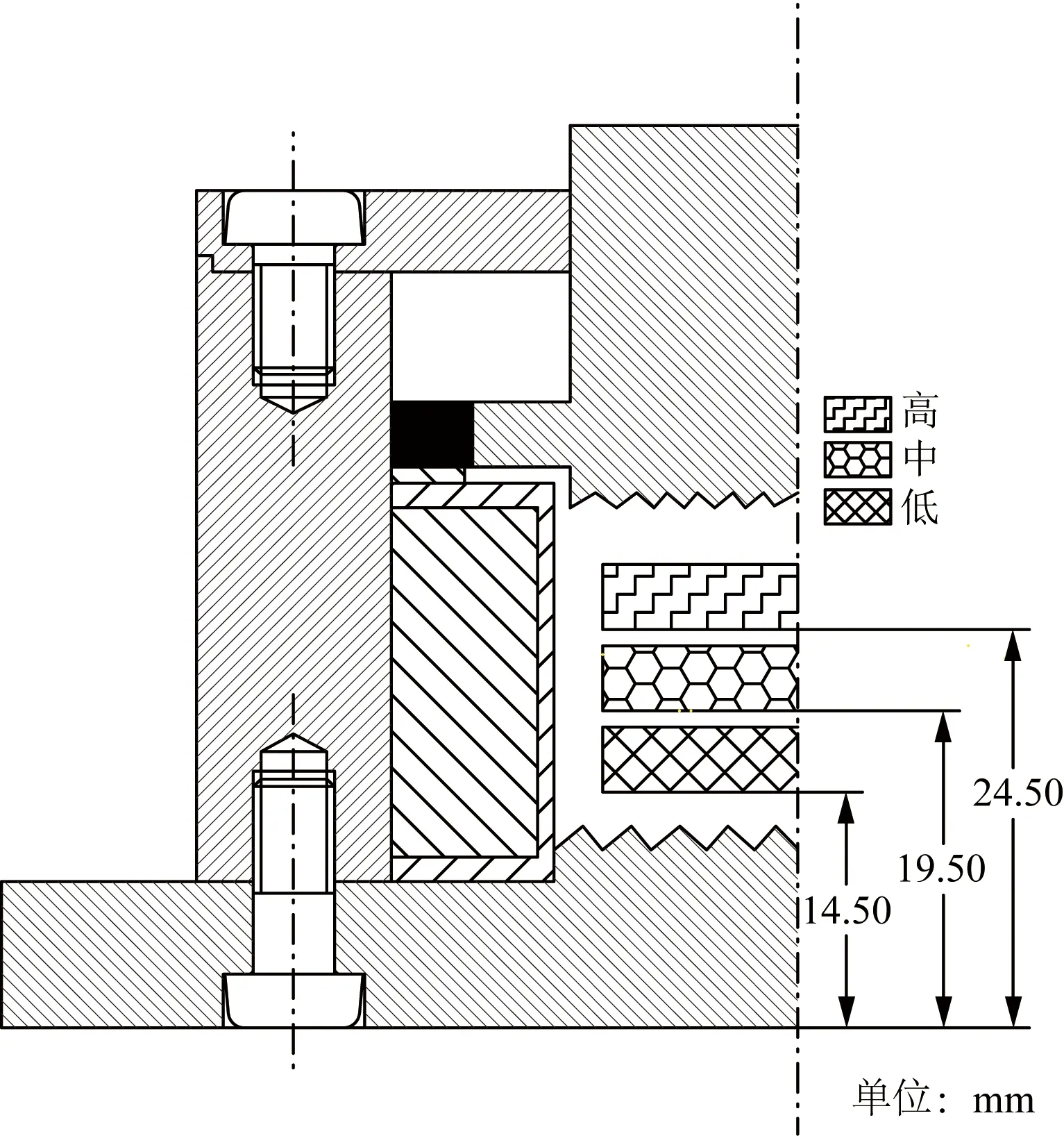
图3 压缩MRE相对位置Fig.3 Relative position of compressed MRE
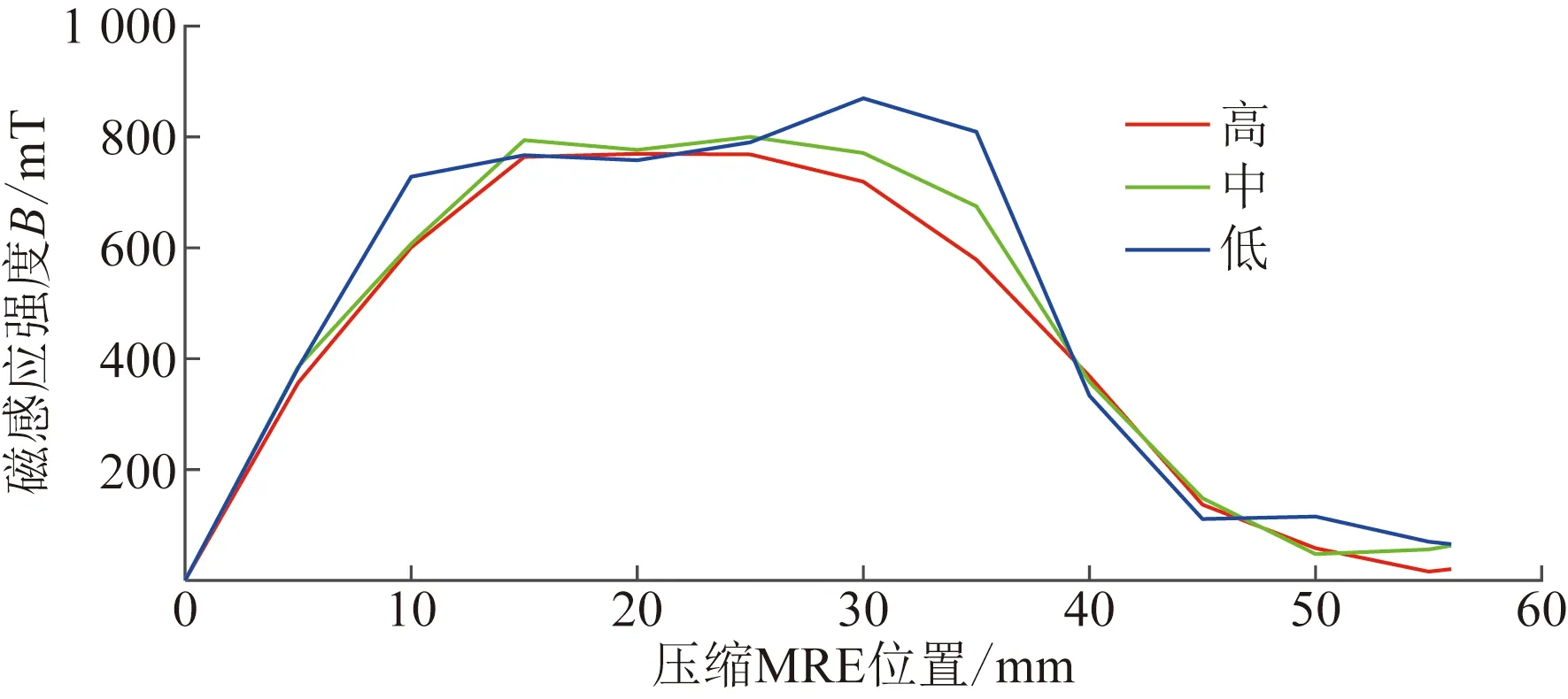
图4 压缩MRE不同位置隔振器中轴线磁感应强度Fig.4 Axial magnetic induction intensity of vibration isolator in different positions of compressed MRE
由图4可知,在压缩MRE所处不同位置时,会对线圈区域(10.5~32 mm)两端磁感应强度产生一定影响,中间区域影响较小,因此压缩MRE只需在线圈中部位置即可,取压缩MRE位置在14~29 mm。
3.2 磁路饱和分析
为最大限度利用所产生的磁场,且达到压缩MRE先饱和的要求,需保证剪切MRE未饱和时磁通量可以满足压缩MRE达到最大饱和磁感应强度时所需磁通量[13]。由式(19)知,由于剪切MRE和压缩MRE的材料饱和磁感应强度相同,若需保证磁通量的数值,只能对面积相关尺寸进行更改[4]。
Φ=BS
(19)
使压缩MRE截面积最大时的饱和磁通量小于等于剪切MRE截面积最小时的饱和磁通量即可计算出边界值,即临界值时压缩MRE最大截面积等于剪切MRE最小面积。最终得出磁路饱和计算结果如表3所示。
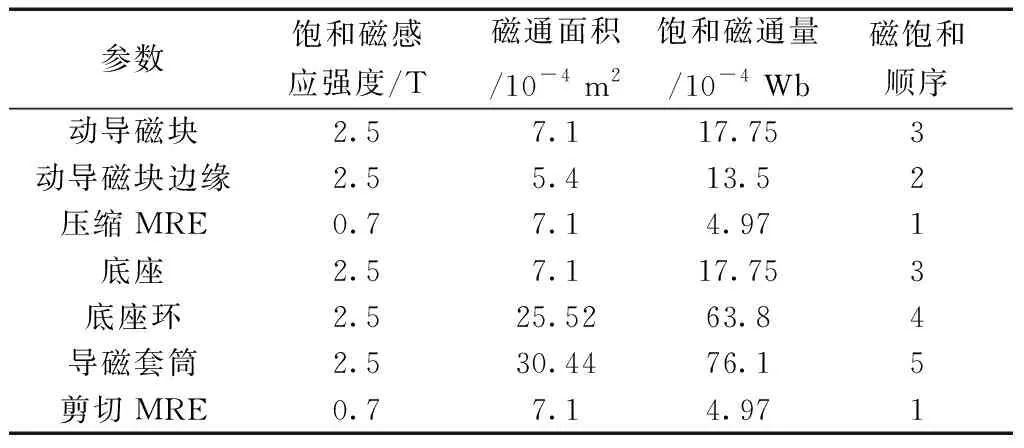
表3 磁路饱和边界值计算结果Table 3 Calculation results of saturation boundary value of magnetic circuit
所设计的尺寸满足磁饱和顺序要求,由所得的剪切MRE的面积可求得当剪切MRE的高h5=5 mm时,其内径r4最小为20.2 mm;当h5=6 mm时,r4最小为12.7 mm。因此,r4的最小值确定为20.2 mm。
3.3 优化变量
优化涉及尺寸有:r1、r2、r4、h2、h3、h4、h5。由于前文已经对半径采用差值约束变量进行表示,对以上半径参数的优化仅需对Δ1-3、Δ2-3、Δ3-4三个差值约束变量进行优化即可。
已知座椅总成及乘员1/4质量为m和MRE许用压应力[σMRE][14]。径强度校核,确定最小半径r1=3.8 mm;线圈龙骨在绕线轴厚度为1 mm;由3.1节中分析过程可以进一步得到h2和h4的取值范围。优化变量及取值范围如表4所示。
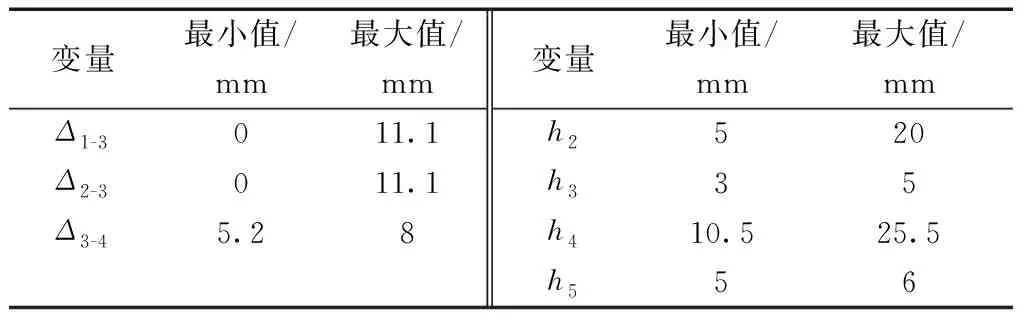
表4 优化变量及取值范围Table 4 Optimization variables and value range
3.4 优化目标及参数确定
建立目标优化函数、定义约束条件以及对该混合式MRE隔振器相关参数进行罗列。
由上述分析可知,混合式MRE隔振器多目标优化有如下2个目标:功率最低和磁致刚度最大,由此建立以下优化目标函数:

(20)
约束条件为
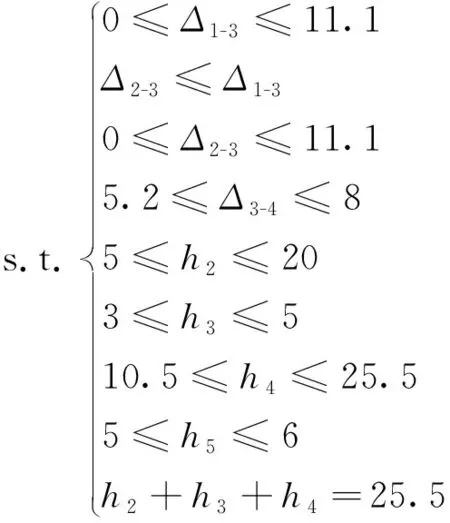
(21)
为使与压缩MRE接触的动导磁块接触面积大于压缩MRE截面积,令Δ2-3≤Δ1-3;为避免高度总体尺寸超出范围,对高度尺寸进行约束,使得h2+h3+h4总体尺寸不变。
混合式MRE隔振器的相关参数如下。负载质量m:70 kg,真空相对磁导率μ0:4π×10-7H/m,相对磁导率μr、μm:1 580、3.5 H/m,导线电阻率ρ:1.75×10-8Ω/m,导线直径d:0.5×10-3m,磁流变弹性体许用压应力[σMRE]:15 MPa。激励电流I:2 A。
3.5 遗传算法优化及最优解分析
由于传统遗传算法单目标优化需对不同目标函数进行线性加权处理,对加权值的选取难度较大且精度不高,所以采用带精英策略的快速非支配排序遗传算法(NSGA Ⅱ)[15],使用MATLAB软件编写目标函数及相关运算过程函数作为总的目标函数Fun,在主程序中定义变量个数、线性及非线性约束条件及相关遗传种群系数,并调用Gamultiobj函数对目标函数Fun进行优化计算,优化流程图如图5所示。
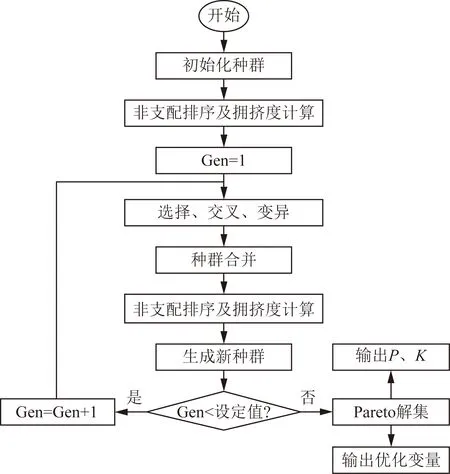
图5 算法流程图Fig.5 Algorithm flow chart
由NSGA Ⅱ求得的Pareto解(图6)可见,目标函数P的增大必然会使另一目标函数K增大,即求功率最小值和求磁致刚度最大值间存在矛盾。
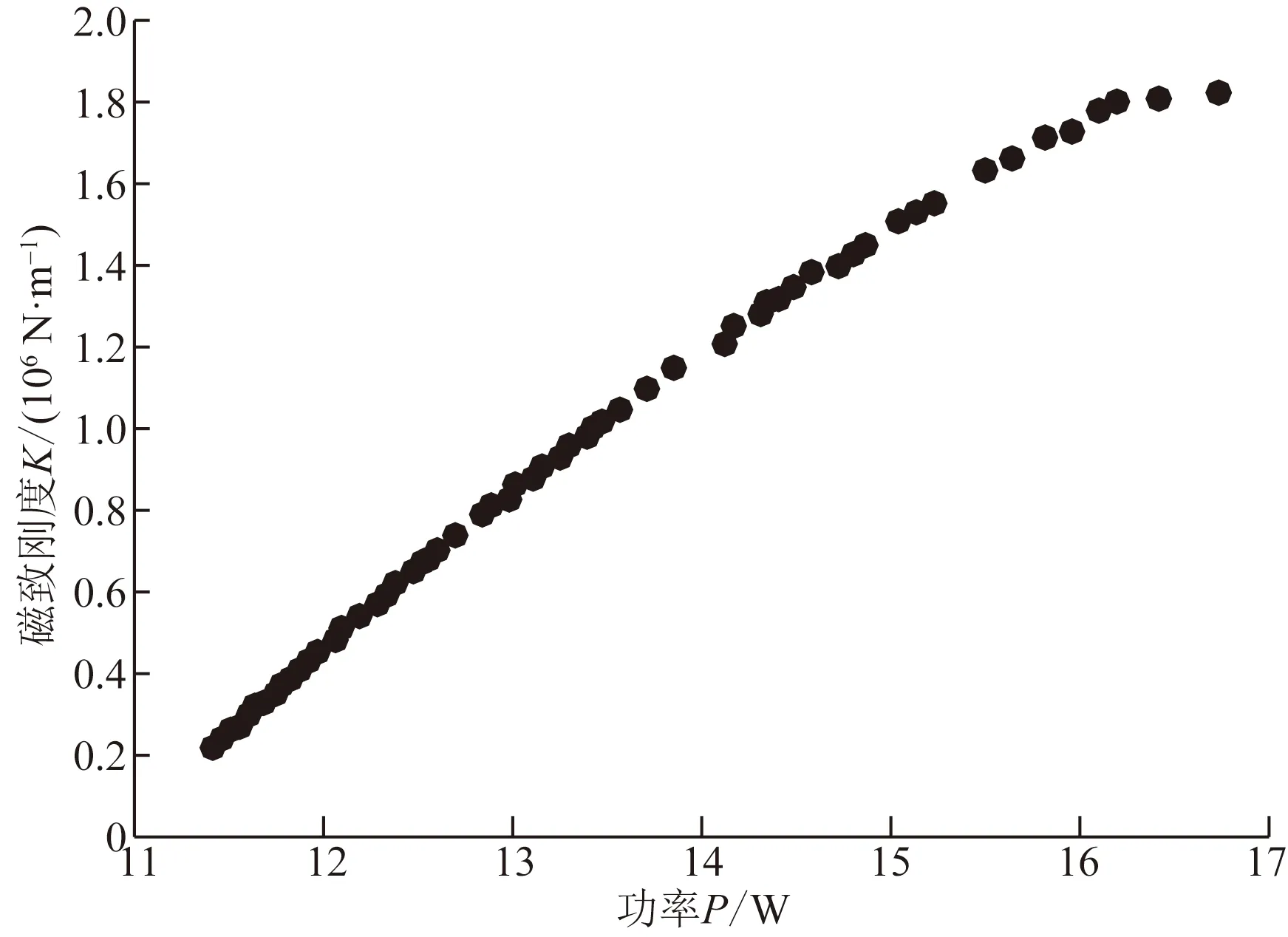
图6 Pareto前沿解Fig.6 Pareto front solution
3.6 有代表性的解
从所有Pareto解中找出最具代表性的三组解,与初始参数对比如表5所示。

表5 优化结果对比Table 5 Comparison of optimization results
由表5中三组优化后的解可以看出,对于本次的优化,第1组结果体现磁致刚度最佳优化效果,最多可以提高174.54%,同时功率降低36.08%;第2组结果体现功率最佳优化结果,最多可降低52.19%,磁致刚度与优化前相同;应为首要目标,第3组结果体现均衡优化,磁致刚度提高49.67%,功率降低48.69%。对于压缩MRE厚度h3、剪切MRE厚度h5及剪切MRE内径r4与磁致刚度呈负相关,与功率成正相关。
4 优化结果仿真
由以上优化结果可知,若要达到对该隔振器均衡优化的目的,第3组数据最为合适,对应的具体尺寸如表6所示。
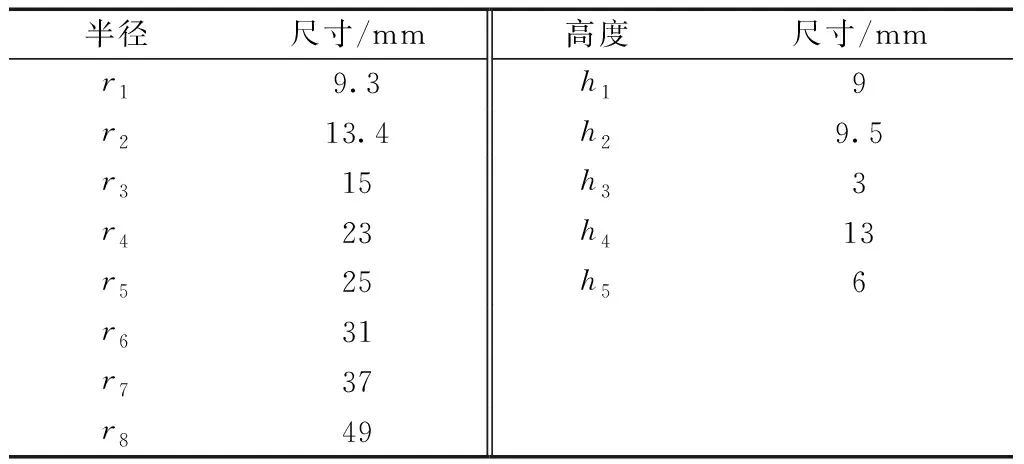
表6 优化后数据值Table 6 Optimized data value
对第3组数据进行计算可知,当激励电流为2 A时,其线圈匝数为291 匝,由于有孔等特征存在,将匝数圆整为300 匝,满足线圈龙骨尺寸要求。
采用Ansoft Maxwell仿真软件第3组数据情况进行磁场仿真分析,结果如图7所示。
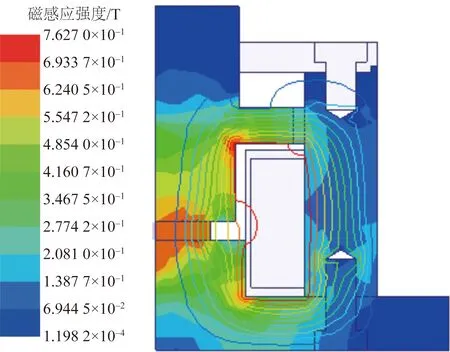
图7 仿真结果Fig.7 Simulation result
由图7可见,在情况3时,压缩MRE首先达到磁饱和状态。压缩MRE和剪切MRE此时的平均磁感应强度分别为691、243 mT。经计算在此情况下混合式MRE隔振器可产生的磁致刚度为1.08×106N/m。与优化计算结果相符。
5 结论
通过对混合式磁流变弹性体隔振器建立数值计算模型、多目标优化设计及仿真分析,可得以下结果。
(1)压缩MRE厚度、剪切MRE厚度及剪切MRE内径与磁致刚度呈负相关、与功率呈正相关。
(2)优化后的隔振器较优化前磁致刚度提高49.67%,功率降低48.69%,优化效果明显。为后续的设计加工及实测提供了正确的尺寸参数及理论指导。
(3)混合式隔振器功率和磁致刚度间相互制约,可根据具体需求于优化结果中选择适合的参数结果。
