城市中心路内停车与停车换乘的动态优化模型

葛啸慈， 石超峰， 庞 利

(1.重庆交通大学交通运输学院， 重庆 400074； 2.重庆交通大学经济管理学院， 重庆 400074)

随着社会经济的发展，中国城市化进程普遍加快。近几年，私家车的拥有量持续上升，这给城市带来了很多问题：停车位紧缺、交通拥堵、环境污染等。城市中心区作为城市公共活动的核心，其丰富的经济、文化、娱乐活动吸引了大量交通需求，也导致了城市中心区的停车需求的增加。据统计，北京市中心区停车位有254.2万个，但北京市的汽车保有量达到了497.4万辆，停车场的停车位是供不应求的。停车场的停车位供不应求则会驱使出行者将小汽车停放在路边，严重影响城市中心区的交通情况。因此，为解决城市中心区的停车以及拥堵问题，建立考虑交通流的城市中心路内停车与停车换乘(park and ride，P+R)的动态优化模型。

中外学者对城市中心区的停车问题提出了很多解决措施，比如停车收费方面，李军等[1]利用logit离散选择模型计算出行者的期望感知价格，制定了公共机构差异化的停车收费方案。Nissan等[2]对比郊区引入停车费、增加中心区的停车费以及罚款金额的前后数据分析发现郊区实行停车费后，停车数量减少了；然而中心区停车费的增加对停车需求影响较小；增加罚款金额对违章停车的车辆数量也没有影响。曹弋等[3]基于随机用户均衡理论，构建了包含地铁、公交、小汽车及P+R这4个选择的logit模型，得出了实行区域差异性停车收费，可以减少小汽车出行的结论。Wang等[4]利用双层规划模型来确定混合管理方案中P+R停车场设施的最优停车费。罗朝晖[5]应用双层规划模型对停车换乘进行拥挤收费定价，不仅改善了道路的拥堵情况，也保证了用户盈余与公平。Mo等[6]利用回归不连续性设计、结构方程模型和二元逻辑回归模型探讨定价政策对路内停车管理的影响，结果表明政策干预后的路内停车收费降低停车量以及停车时长。以及寻找停车位方面，Diana等[7]提出一种路边停车位在线预约系统，利用观测数据建立交通和巡航行为模型并进行检验，最后，通过仿真比较不同情况下的车位分配情况。结果表明，在有预约的情况下，总旅行时间得到了全面改善；关颂衡等[8]利用“停车服务水平”的指标来描述车主能够找到停车位的概率，建立考虑泊位利用率的停车服务水平最大化的优化模型，同时从停车价格和停车位数量两个方面优化调整路内停车的收费方案，并用案例证明了模型的合理性。Arnott等[9]分析了当私人运营商提供车库停车时，将出行需求分为低、适中、高三种情况下的路内停车位的分配方法。严海等[10]根据深度优先搜索算法建立仿真模型，对路内预约停车位设置方法进行研究，研究表明，预约车位位置和预约车位比例对停车效率有影响。关宏志等[11]在P+R停车位不足的情况下，利用周边社会停车场联合经营，运用多项logit模型(multinomial logit， MNL)和巢式logit模型，构建了出行者换乘失败后的选择行为模型。

综上可知，国内学者在城市中心区的停车问题方面，大多单一考虑停车收费或者停车容量对停车的影响，未能很好地将停车费和停车容量以及交通流深入结合研究；且当P+R加入时，很少考虑路内停车的收费和停车容量对P+R的收费和停车容量是有影响的。因此，有必要将交通流、路边停车和P+R统一模型研究。基于此，现在路内停车与市区交通拥堵存在内在关联性的基础上，建立存在路内停车的短期最优流率模型，以及同时考虑路内停车以及P+R的停车容量博弈模型，以期为缓解城市交通拥堵、路内停车管理提供理论基础，对车道控制理论和技术有一定指导意义。

1 路内停车与市区交通拥堵的内在关联性

1.1 不存在停车的市区交通拥堵问题

为了分析城市中心区的停车问题，首先考虑市区的交通拥堵问题。为了进一步分析奠定基础，忽略市中心的停车问题来考虑市区的拥堵问题。假设市中心是由单向街道组成的网络，市区停车是无成本的，不占用街道空间，且所有的出行方式都是开车。

在此情况下，用户出行成本为

UC=ρmt

(1)

式(1)中：ρ为出行者的时间价值；m为出行距离；t为每千米的旅行时间，t是一个关于交通密度K的函数。根据格林希尔治速度-密度线性模型：

(2)

式(2)中：v为交通流区间平均速度；vf为自由流速度；Kj为阻塞密度；K为交通流密度。可推导出：

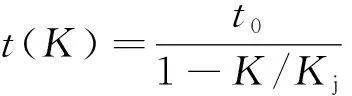
(3)

式(3)中：t0为自由流下出行者行驶1 km所用的时间，t(0)>0。定义用户出行全价=用户出行成本+通行费，即

F=UC+τ

(4)

式(4)中：τ为通行费。单位面积时间内的出行需求D是固定的，是出行全价的函数。在稳态条件下，单位面积时间内初始出行数等于单位面积时间内终止的出行数。单位面积时间内的稳态出行数为流率，用r表示。且它由需求函数给出：

r=D(F)=D0F-α

(5)

式(5)中：D0为需求强度；α为需求弹性。单位面积时间内终止的出行数等于交通密度除以每辆车在交通中花费的时间。因此，稳态条件为

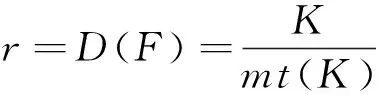
(6)

这种稳态条件可以用图1来表明。

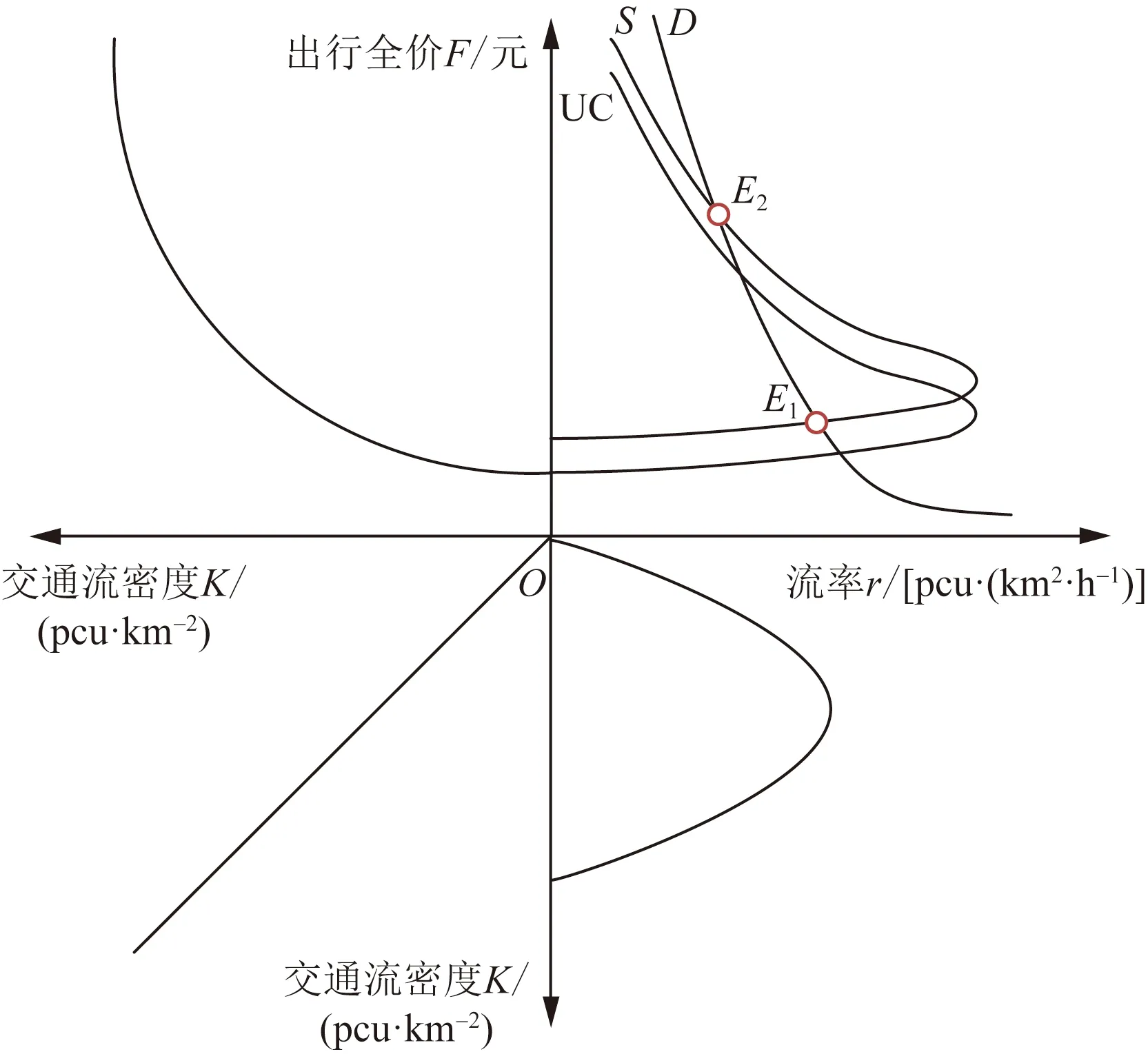
pcu为标准车当量数，也称当量交通量图1 供需均衡Fig.1 Balance of supply and demand

供给曲线有正斜率和负斜率，向上倾斜部分的曲线称为拥挤行程，向后弯曲部分的曲线称为超拥挤行程。拥挤的旅行是正常状态下的旅行，速度随着流率的增加而下降。超拥挤旅行与交通堵塞情况相对应，速度随着流率的增加而增加。其中E2点为交通流拥堵的均衡点，E1点为交通流超拥堵时的均衡点。在交通流超拥堵时，路内停车需求远大于供给，此时，路内停车问题将演化为车道控制问题。在此不考虑交通流超拥堵即交通堵塞的情况。

将图1中的第一象限供给曲线的向上倾斜部分放大形成图2。在图2中的用户成本曲线上，边际社会成本被定义为总用户成本相对于流率的导数，等于用户成本加上拥堵外部性成本。(社会最优)最优值(图2中标记为O)位于边际社会效益曲线(与逆需求曲线重合)和边际社会成本曲线的交点处。(用户均衡)平衡点，在图2中标记为E，位于需求曲线和用户成本曲线的交点处。

MSC为边际社会成本曲线；MSB为边际社会收益曲线；D为需求曲线；这里边际社会收益曲线与需求曲线重合；FO为系统最优下的出行全价；FE为用户均衡下的出行全价；F1为UC曲线达到系统最优流率下的出行全价；rO为达到系统最优的流率；rE为达到用户均衡的流率图2 用户均衡与系统最优Fig.2 Balance and system optimization

由于出行者出行只考虑用户出行成本，只能达到用户均衡，因此，为了使得系统达到最优，可以通过收取一定的费用FO-F1，让UC曲线向上平移，使得用户均衡点与系统最优点重合，即E点与O点重合，达到最优流率。在该情况下，图2中AOE的面积则可以作为未进行拥堵收费定价时产生的无谓损失。这也说明了增加一定的收费会使得道路不那么拥挤，此时的通行费的价格应等于FO-F1。

1.2 只有路内停车的市区交通拥堵问题

现在对没有停车的市区交通拥堵模型进行修改，假设司机必须停车，且只有路内停车，不存在车库停车。当只存在路内停车时，需要考虑以下4个方面的问题：第一，增加了用于停车的道路空间，也就减少了交通流使用的道路空间，从而降低了道路拥挤密度；第二，路内停车容量限制了流率不能超过车位的周转率；第三，当给定停车费，没有足够的停车位来满足停车需求时，就会发生巡航行为；第四，路内停车费对控制路内停车容量起关键性作用。

为了简化，提供一个简单的停车搜索方法：假设每个司机都需要行驶一段固定距离到达市中心的目的地，如果有停车位，他就会选择停车；如果没有停车位，他就会在目的地附近开车，直到有空位，在目的地访问一段时间后开车离开。因此，行驶距离以及访问时间是固定的。

在存在路内停车的市区交通拥堵的模型中，当路内停车位饱和，即路内停车位均被占用时，路内停车位的周转率为P/l，其中P为单位面积的路内停车位密度，l为车辆停放时间。由于流率不能超过路内停车位的周转率，因此有路内停车约束：r≤P/l。

(7)

式(7)中：Ω为无路内停车时的拥挤密度。其次需要考虑到车辆的巡航停车以及交通流车辆与巡航停车之间的拥挤。假设巡航车辆对交通流的影响是正常车流的θ倍，则交通流密度K=T+θC。那么行程时间可表示为

(8)

式(8)中：T为单位面积内正常行驶车辆的车辆密度；C为单位面积内巡航停车的车辆密度。

2 存在路内停车的短期最优流率模型

城市中心区的停车位供需不平衡导致了停车需求得不到满足，带来一系列停车问题以及拥堵问题[12-13]。当停车位不收取停车费时，道路上的流量则处于无约束的状态。此时，若交通量较大且处于无约束状态时，道路交通秩序则会发生混乱，也会产生交通拥堵、大量巡航停车以及违规停车等一系列问题。外国通过收取道路拥挤费来限制交通量，而中国目前尚无明文规定收取道路拥挤费，因此，管理部门会将交通出行产生的这些问题都与停车问题结合起来，也就是中国停车收费的本质是将交通拥挤以及路内停车所产生的外部性成本转化为内部性成本。

2.1 问题描述及模型假设

研究短期情况下即路内停车容量固定的情况下，利用路内停车的稳态条件以及停车容量的约束，求解最优流率，使得社会剩余最大。在该情况下，没有巡航停车则是最优的选择，因为没有它，同样的流率(也可以说同样的社会效益)可以以更低的成本实现。因此，短期最优流率模型不考虑巡航停车，即式(8)中C=0。

2.2 模型建立与求解

当路内停车容量是固定的，模型的问题就是在稳态条件和路内停车容量的约束下，选择流率r和单位面积内正常行驶车辆的车辆密度T使社会剩余最大化。对于流率r来说，稳态条件满足两个T值：较低的值表示交通拥挤出行，较高的值表示交通流超拥挤出行。流率r水平下的社会效益用B(r)表示，即(0,r)区间内的需求曲线下的面积。社会成本用ρT表示，为了给出最优流率的计算公式，需要求解如下最优流率模型，其优化目标为社会剩余最大化：

(9)

(10)

(11)

式(9)为目标函数；式(10)为稳态条件，表示单位面积时间内初始出行数等于单位面积时间内终止的出行数式(11)表示路内停车约束。

图3给出了对应不同需求强度水平的曲线D1、D2，其中，CPC为路内停车容量约束。将式(8)中令C=0后代入式(10)中，整理得

T2-TKj+rmt0Kj=0

(12)

由求根公式可得

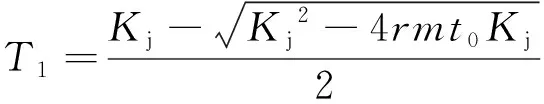
(13)

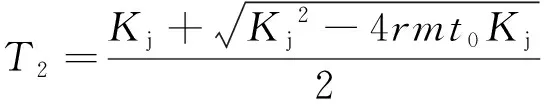
(14)

式中：T1为T的较小根，对其求r的偏导可表示为∂T1/∂r，ρ(∂T1/∂r)则描绘了不同流率下的短期社会边际成本，也就是图3中的SRMSC曲线。

对于需求曲线D1，不受路内停车约束的影响，社会最优点O1在需求曲线与SRMSC曲线交点处。由于假设路内停车所引起的拥堵密度的降低取决于分配给路边停车位的数量，而不受其占用率的影响，因此不产生停车外部性成本。此时，短期边际社会成本等于用户成本加上拥堵外部性成本，从而可以通过将通行期间的停车费设为拥堵外部性成本(图3)来分散社会最优。

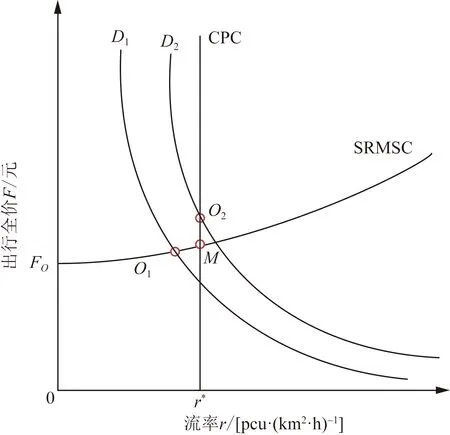
r*为路内停车容量约束条件下的流率图3 只有路内停车的短期最优流率Fig.3 Only the short-term optimal flow rate for on-street parking

在需求曲线D2下，路边停车容量约束固定，社会最优点O2位于需求曲线与路边停车容量约束的交点。此时的短期边际社会成本等于用户成本加上拥堵外部性成本加上停车位稀缺租金，停车位稀缺租金是O2和M之间的垂直距离，M是由SRMSC和CPC的交点给出。通过将拥堵外部性成本与停车稀缺租金相加，可以实现分散的社会最优。

3 同时存在路内停车和P+R的短期停车容量博弈模型

3.1 问题描述及模型研究

研究短期情况下即车位容量总量固定，路内停车位和换乘停车场车位未知的情况下(即在不改变现有总车位数量或不对车位数进行规划的情况下)，通过经济杠杆的方式来进行调控，消除巡航停车，缓解交通拥堵、停车难等问题。在该情况下，车位数量总数是已知的，但停车收费价格随着停车需求变化而变化，考虑高峰出行的停车定价问题，利用模型求解可得到路内停车位与换乘停车场的停车位最优分配情况以及分别对应的最优停车收费定价。

生活区O远离城市中心区，工作区D位于城市中心区，城市中心区附近停车场车位已经停满，只有路内停车位可以停车。P+R停车场位于城市中心区以外靠近轨道交通站点，可供上班人群换乘轨道交通进入城市中心区。出行者每天早晨从O出发去D，有两种交通方式可以选择，方式一是自己全程开车到目的地，即选择路内停车的流量为f1，出行距离为m；方式二是开车到换乘停车场，出行距离为m1，然后换乘轨道交通到工作区，即选择P+R停车的流量为f2。选择自己全程开车到工作地上班，早高峰会产生巡航行为，需要考虑巡航成本，而选择开车到停车场，再进行换乘则需要考虑停车换乘成本以及政府对选择换乘出行的补贴。总停车位容量为s，路内停车位为s1，换乘停车场车位为s2，s=s1+s2。路内停车收费价格为τ1，运营成本为b1；私人运营商收费价格为τ2，运营成本为b2。模型假设如下：假设出行者出行均选择同种类型的小汽车；路内停车位所属权归于政府，换乘停车场所属权归于私人运营商，政府追求社会总成本最小，私人运营商追求利润最大。

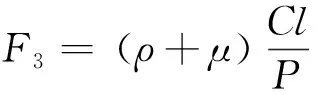
以出行者选择开车到换乘停车场，进行轨道交通换乘到目的地的出行全价包括用户出行成本F1=UC=ρmt、燃油消耗成本F2=μmt、换乘停车场停车费F4=τ2l-γfl及停车换乘成本F5=M+ρts+σf2。换乘停车场停车费包括私人运营商对P+R停车位的收费τ2l以及政府对选择P+R出行者的补贴γfl，γ为政府对选择P+R出行的引导系数。停车换乘成本包括轨道交通票价M、乘坐轨道交通的时间成本ρts以及轨道交通车厢内的拥挤成本σf2(ts为轨道交通车厢内花费的时间、从换乘停车场到轨道交通站点的步行时间成本以及等待轨道交通的等待时间),σ为轨道交通车厢内的拥挤成本系数。因此，出行者开车到换乘停车场，然后换乘轨道交通到目的地的出行全价F′=ρmt(k)+μmt(k)+M+ρts+σf2+τ2l-γf2l。

当出行者选择路内停车时，考虑通行成本、巡航成本以及停车费，其出行成本为

(15)

当出行者选择P+R停车时，考虑通行成本、换乘成本以及停车费，其出行成本为

C2=ρmt(k)+μmt(k)+M+ρts+σf2+

τ2l-γf2l

(16)

3.2 模型建立与求解

同时考虑路内停车和P+R的最优停车容量模型用博弈论中的Stackelberg博弈[14-15]来描述，即政府是领导者，通过控制路内停车位的车位数量以及收费价格来达到社会总成本最小；私人运营商是跟随者，以政府定价为参考，通过控制换乘停车场的车位数量和收费价格来达到利润最大化；出行者是最下层的跟随者，在前两者基础上追求用户出行成本最小。

在上面的博弈模型中，首先考虑用户均衡模型。出行者在C1=C2时达到用户均衡，此时可以得到选择路内停车的流量f1以及选择P+R停车的流量f2：

(17)

f2=f-f1

(18)

式中：f为道路总车流量。对f1分别求路内停车收费价格τ1以及换乘停车收费价格τ2的偏导数可得

(19)

(20)

政府追求社会总成本最小，即除去停车费以及票价以外的总成本最小：

minR=(C1-τ1l)f1+(C2-M-τ2l)f2+

b1s1+b2s2

(21)

式(21)对τ1求偏导并且令其偏导数为零可得

(22)

将式(17)代入式(22)中，可以得出τ1与τ2之间的关系式：

(23)

将式(23)代入式(18)中，可以得出f1与s1的函数关系式：

(24)

私人运营商追求利润最大，即

maxW=τ2f2-b2s2=τ2(f-f1)-b2(s-s1)

(25)

式(25)对τ2求偏导并且令其偏导数为零可得

(26)

由式(26)解出s1的表达式为

(27)

式(27)对s2求偏导并且令其偏导数为零可得

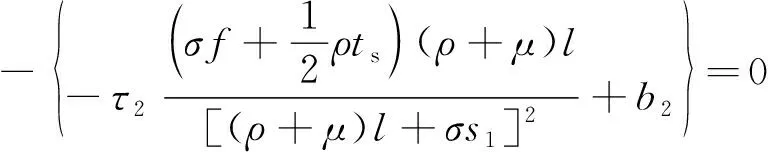
(28)

根据式(23)、式(24)、式(27)、式(28)以及f=f1+f2，s=s1+s2可以分别求出τ1、τ2、f1、f2、s1、s2的解。从而可以得到出行者两种出行方式的流量、路内停车费、P+R停车费以及路内停车位和换乘停车场的车位数量。

4 数值算例

本节用一个算例对上述模型进行求解。在需求固定的情况下，即现有车位总数量不发生改变，通过Stackelberg博弈模型从政府和私人运营商两方面建立目标函数进行求解。参数取值如表1所示。

表1 参数赋值表Table 1 Parameter assignment table

根据不同的车辆停放时间来求解路内停车容量、路内停车费以及P+R停车容量、P+R停车费，计算结果如表2所示。

表2 不同停车时长的停车容量Table 2 Parking capacity for different parking hours

从表2可知，随着车辆停放时间的增加，路内停车费与P+R停车费都在不断下降，路内停车容量在不断减少，而P+R停车容量不断增加，这说明如果选择短时停车或者临时停车，可以选择路内停车；而如果选择长时间停车，可以选择P+R停车。这也基本符合路内停车位适合停放临时办事的车辆，P+R停车位适合上班人员停放车辆再进行换乘到达城市中心区这一事实。

路内停车位的收费价格高于换乘停车场的价格则促使居民选择停车换乘的方式出行，降低小汽车进入城市中心区的比例，减少市中心的交通拥堵。

在停车收费方面，政府可以根据车辆停放时间实行差别化收费，对于短时路内停车进行少收费，对于长时间路内停车，增加单位停车费。在寻找停车位方面，利用停车诱导技术，规划停车路线，减少巡航停车。在P+R停车方面，政府可对选择换乘的居民进行补贴，从而诱导P+R出行，减少小汽车进入城市中心区，缓解交通压力。在优化城市交通流方面，交管部门可以进行小汽车单双号限行。

5 结论

停车问题是城市中心区的交通问题的重要组成部分，而目前中国关于停车问题的研究大多集中在停车收费上，提高停车周转率有利于缓解城市中心区的停车供给不平衡和拥堵问题。根据供需均衡原理探讨了不存在停车的城市中心区的交通拥堵问题，得出可以通过收取一定的通行费使得系统最优。在城市中心区存在路内停车的交通拥堵模型中结合交通流来动态调整路内停车资源，加快路内停车周转率。且在交通需求远大于供给时，可以发现路内停车问题会演化成车道控制问题。

建立了路内停车的短期最优流率模型，确定最优流率和最佳车辆密度，实现社会剩余最大化；运用Stackelberg博弈模型从政府和私人运营商两方面建立目标函数，求解同时存在路内停车和P+R的短期最优停车容量。通过价格调节机制，避免长时间停车，实现最优周转流率。并通过数值算例，验证短时停车或者临时停车可以选择路内停车，而如果长时间停车可以选择P+R停车。在下一步研究中，将考虑经济学中定义为长期即需求可变的情况，并利用实际数据，对其进行验证。