城市无人机毫米波通信网络建模与性能分析

2021-11-22卫海超刘铭岳张家红许爱德

科学技术与工程 2021年30期

卫海超，刘铭岳，张家红，许爱德

(大连海事大学信息科学技术学院，大连 116026)

无人机具有视距通信概率高，覆盖范围大和可灵活部署的优点，近年来,在广泛的应用场景中发挥重要作用[1]。例如，在有重大赛事发生的热点地区，用户对通信的需求量可能会在短时间内激增，无人机可以作为一种快速部署的临时基站或空中中继，帮助地面蜂窝网络卸载一部分流量，提高服务质量[2-3]，或在现代军事战争中，作为备份通信系统的中继节点部署在战场中[4]。为了研究无人机通信如何影响蜂窝通信，目前已有一些文献研究了无人机通信网络的性能[5-8]。其中，为了研究大规模网络场景下无人机通信性能，诸多研究采用随机几何的理论工具对无人机空间分布特性进行提取建模，并加以理论分析。文献[5]提出了一种无人机基站协助地面基站协作提供服务的下行通信系统，其中无人机基站和地面基站在水平面上的投影位置分别服从两个独立的泊松点过程(poisson point process, PPP)，推导了典型用户分别与无人机基站和地面基站建立通信连接的概率，进一步推导得出了系统覆盖率，结果显示存在最优无人机部署高度使系统覆盖率最大化。文献[6]将由地面微基站和空中基站中组成的双层网络分别建模为泊松点过程和二项式点过程(binomial point process, BPP)，并引入了一个包含视距(line-of-sight, LOS)和非视距(non-line-of-sight, NLOS) 的信道概率模型，推导出了系统覆盖率和频谱效率。文献[7]提出了一种城市地区无人机通信网络的模型，考虑城市环境中密集的建筑物对通信链路的遮挡，服务无人机的选择遵循接收功率最大化原则，而非以距离最近无人机来服务，进一步推导了该模型下的系统覆盖率。文献[8]考虑到无人机作为空中基站时在空间上的多层结构，当小尺度信道衰落分别为伽马分布和指数分布时，分别推导了对应的典型小区中的系统覆盖率的闭式表达，进一步推导出了频谱效率，结果显示存在最优无人机部署密度使频谱效率最大化。

然而，以上研究中，无人机的通信频段均为微波频段。随着5G时代的到来，人们对无线通信业务的需求呈指数式增长，频谱资源匮乏的问题日趋严重。毫米波频段(30～300 GHz)具有丰富的尚未开发利用的频谱资源，是未来无线通信的必然选择。然而，毫米波传输损耗严重，高路损，大气衰减和雨衰减严重限制了毫米波信号的传输距离。而无人机由于具有动态部署的特性，在通信过程中可以作为毫米波通信技术的绝佳搭载平台。例如，将无人机搭载毫米波雷达进行输电线路巡检[9]和植物保护中测量高度[10]等工作。综上可见，将无人机与毫米波技术结合以弥补毫米波的固有缺陷，是未来具有前景的无线通信技术之一。

对于毫米波技术和无人机通信相结合的通信场景，文献[11]提出了一种通用性的3D空间框架，来建模在未被基站覆盖区域，用户将信息发送给无人机中继，无人机飞行到基站覆盖区域再将信息进行转发的毫米波通信网络。但是无人机的飞行过程会造成通信时延，不适用于及时通信。文献[12]针对灾害应对等需要在有限区域内部署固定数量无人机的场景，将无人机的位置建模为有限区域内的二项式点过程(BPP)，构建了一种三维平面内无人机支持的毫米波网络模型。文献[13]提出了一种通用性的3D空间模型来建模毫米波网络中无人机到用户的下行链路，其中假设无人机装备3D天线阵列，天线阵子通过调整方位角和仰角改变天线功率增益，进而影响系统性能。文献[14]考虑了5G集中化无线接入网(centralized radio access network, C-RAN)架构对分布单元和中央单元分开独立部署的要求，利用无人机搭载分布单元，与部署在地平面上的中央单元建立前传链路时的性能进行了分析，对比了该架构工作在毫米波和微波频段时的中断概率

现有研究中，文献[11-12]对城市地区的无人机毫米波网络建模时，将系统的视距链路概率建模为关于仰角的函数，然而，这种建模方法无法分析建筑物的某一特定属性(如高度、密度、水平尺寸、方向、位置等)对视距链路概率的影响。为了分析单一特性对无人机网络的影响，文献[13-14]将城市中的建筑物建模为无人机到用户的水平连线上均匀分布的点，利用几何关系推导得到该模型的视距链路概率，进一步分析了系统性能。然而，这种建模方法一方面忽略了建筑物的水平尺寸和方向对视距概率的影响，另一方面也没有体现城市中建筑物位置分布的随机性。文献[7]提出了一种考虑了建筑物自身属性影响的微波波段的无人机通信网络模型，但毫米波波段固有的高路损特性使得该模型及对应的理论结果不适用于毫米波网络。受到这些启发，综合考虑城区建筑物分布特性与毫米波传输特性，现提出一种城市地区无人机辅助的毫米波网络模型，并基于提出的模型推导出覆盖率的近似表达式；综合考虑无人机配备定向天线阵列弥补毫米波的高路损，以及城市中建筑物在尺寸、高度、方向上具有的随机性对毫米波网络系统性能的影响。推导的理论结果可用于评估指定环境参数下无人机毫米波网络的系统性能，以期对未来实际无人机中继的部署具有先验指导意义。

1 系统模型

1.1 网络模型

选取处于建筑物的3D环境下的无人机无线通信网络作为研究对象，其系统框架如图1所示。首先考虑城市中的建筑物，一般地，假设城市中的建筑形状通常为长方体结构，它们的水平尺寸、高度和方向都是随机的、相互独立的，中心点构成一个2D平面上的均匀的泊松点过程，强度为λB。假设每个建筑物的长L和宽W的分布服从特定的概率密度函数fL(y)和fW(y)，其期望分别为E[L]和E[W]。建筑物的方向角用φ来表示，在(0,2π]上均匀分布。建筑物的高度hB服从瑞利分布，其概率密度函数为

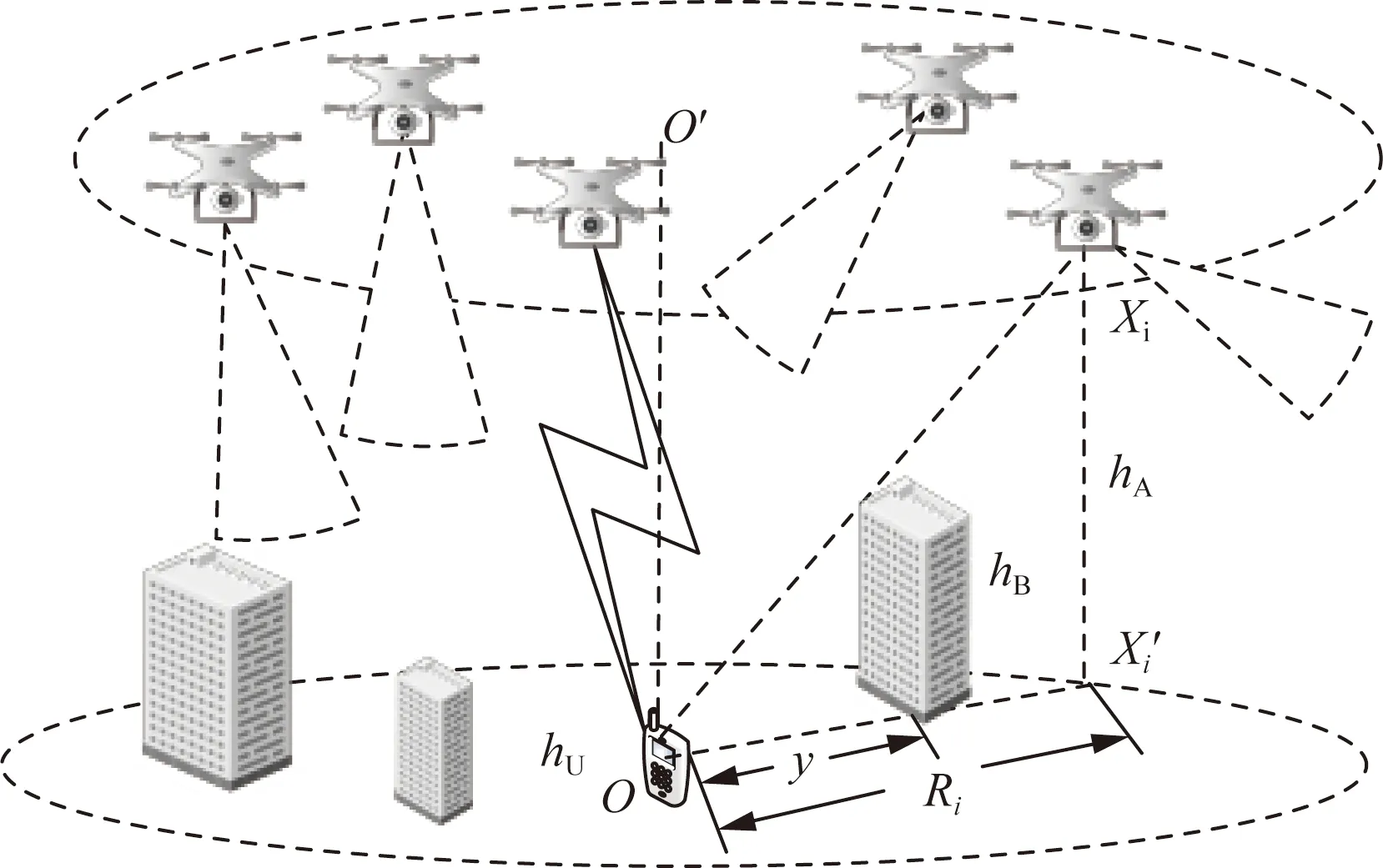
hA为无人机高度;y为建筑物到用户的距离;X′i为无人机在水平面上的投影;hB为建筑物高度;Ri为无人机i到用户的水平距离;O为用户位置;hU为用户高度;Xi为无人机的位置;O′用户在无人机平面上的投影图1 系统模型Fig.1 System model

(1)

式(1)中：σ为瑞利分布的尺度参数。

1.2 天线模型

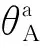
(2)

式(2)中：ζi(i=1,2,3,4)为G的分布概率；p1、p2分别为无人机端和用户端的天线主瓣对齐的概率。用下标c∈{A,U}表示无人机端和用户端，则

(3)

(4)

Gc=Nc,c∈{A,U}

(5)

(6)

1.3 信道模型

综合考虑毫米波信道的大尺度衰落项和小尺度衰落项。由路径损耗造成的大尺度衰落可以表示为(d)=d-α，其中d为无人机到用户的距离，α为信道的路径损耗指数。

假设1假设位于毫米波通信链路上的建筑物对毫米波信号完全阻挡，即毫米波不能穿透建筑物。

假设2小尺度衰落信道为Nakagami信道，信道功率增益为一个伽马随机变量z，其概率密度函数为

(7)

式(7)中:m为Nakagami信道的形状因子(shape factor);Γ(m)为m的伽马函数。

Γ(m)=(m-1)!

(8)

2 性能分析

由于系统中无人机和用户均装配定向天线，与干扰的功率相比，系统内的环境噪声可以忽略不计。因此只考虑用户端接收到的信干比(signal-to-interference ratio, SIR)作为性能评估的参数。在3D网络模型及对应的假设条件下，下行链路中典型用户接收到的信干比可以表示为

(9)

式(9)中：R0、Ri分别为典型用户到服务无人机和干扰无人机i的水平距离；Si为OXi链路上的建筑物造成的总穿透功率损耗；z0、zi分别为服务链路和干扰链路的小尺度衰落项。干扰可以表示为

(10)

则覆盖率可以进一步表示为

PCOV(T)=P(SIR>T)=Ex[P(SIR>T)]=

(11)

式(11)中：fR(x)为典型用户到无遮挡且距离最近的无人机的距离的概率密度函数;T为接收端能正确解调信号的信干比门限。

由于无人机到用户的小尺度衰落信道为Nakagami信道，即功率增益z0为服从伽马分布的随机变量。令

w(x)=mTG1-1[(hA-hU)2+x2]α/2

(12)

则式(11)可以进一步推导得到式(13)。

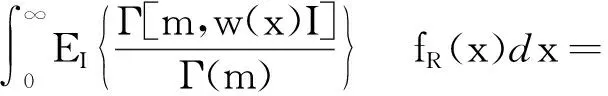
fR(x)dx

(13)

式(13)中：Γ[m,w(x)I]为上不完全伽马函数。

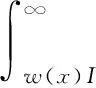
(14)

2.1 距离的概率分布

引理1根据本文3D遮挡模型，典型用户到距离最近的可视无人机的距离x的概率密度函数[7]为

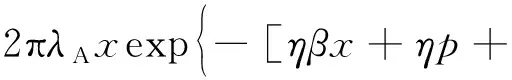
(15)

式(15)中：

(16)

p=λBE[L]E[W]

(17)

(18)

g(x)=1-(ηβx+1)e-ηβx

(19)

证明：由文献[16]可知，位于OX′通信链路上的建筑物数量K′为泊松随机变量，且满足

E[K′]=βR+p

(20)

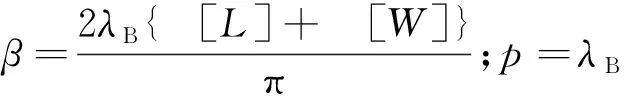
如图1所示，考虑一个建筑物位于OX′链路上，距离点O的距离为y。由几何关系易证，该建筑物只有当其高度hB>[yhA+(R-y)hU]/R时，才会对OX之间的通信链路造成遮挡。因此，已知一个建筑物位于OX′上，建筑物的高度服从瑞利分布，则其对OX造成遮挡的条件概率可以表示为

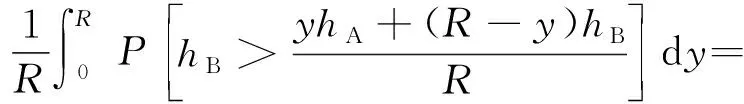
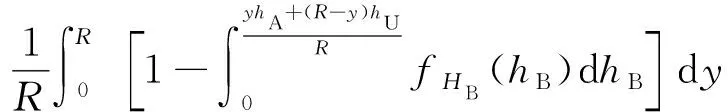
(21)

令s=y/R代入式(21)得

(22)

因此，由细化准则，对链路OX造成遮挡的建筑物数量K是泊松随机变量，其期望为E[K]=ηE[K′]=η(βR+p)。由假设1，建筑物不可被穿透，则总穿透损耗为伯努利随机变量，其概率分布为

P(Si=0)=e-η(βR+p)

(23)

P(Si=1)=1-e-η(βR+p)

(24)

不失一般性地，假设用户位于原点O，点O′为用户在无人机平面上的投影。则可以看出，用户与距离最近的可视无人机的距离R大于某个值x，当且仅当所有位于圆C(O′,x)范围内的无人机与用户之间的链路被遮挡时实现。由泊松点过程的定义可以得到无人机数量的概率分布为

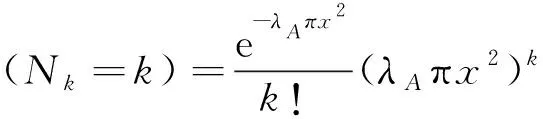
(25)

定义事件M为没有视距通信无人机位于圆C(O′,x)内。由全概率公式，可推得典型用户到距离最近的视距无人机的水平距离的互补累积分布函数为

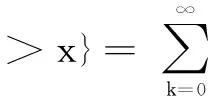
(26)

使用ex的泰勒展开式，式(26)可以进一步推导，得

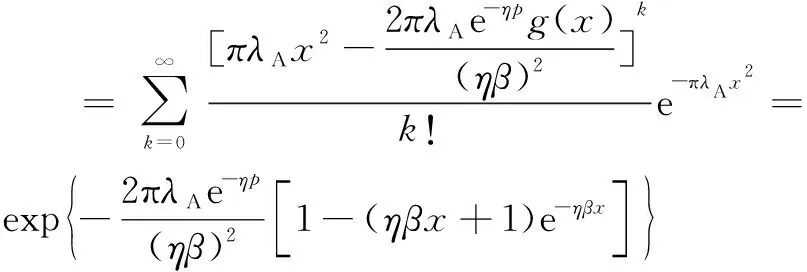
(27)

因此，距离的概率密度函数fR(x)可以通过对式(27)求导数的相反数，得

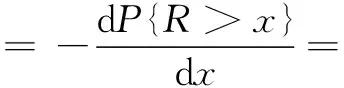
(28)

2.2 覆盖率分析

虽然式(13)中不完全伽马分布的互补累积分布函数可以通过对总干扰求拉氏变换，然后进行数值积分的方法计算得到，但是伽马分布的形状参数m越大，不同阶导数所需要的计算复杂度也越高。为了便于分析，因此，给出更容易计算的表达式来近似评估系统的覆盖率性能。

定理1当典型用户与服务无人机的水平距离R0为x时，其条件覆盖率可以近似表示为

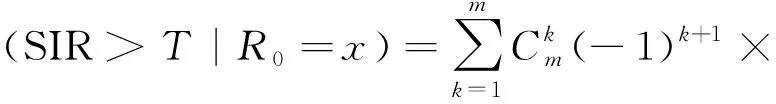
(29)

式(29)中：

(30)

(31)

(32)

证明：从文献[17]可知伽马分布存在如下不等关系:

(33)

式(33)中：

(34)

将式(33)代入式(13)，可以推导条件覆盖率的上界为

P[SIR>T|R0=x]=

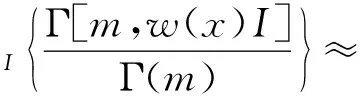
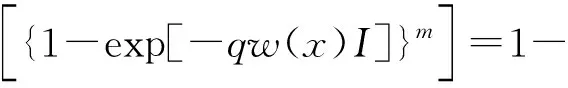
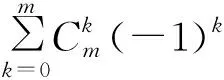
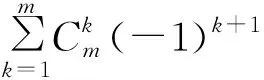
(35)

式(35)中：

EI{exp[-kqw(x)I]}=

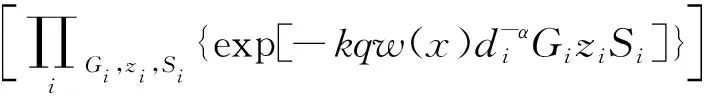
(36)

式(36)中：Si为参数为e-η(βRi+p)的伯努利随机变量[6]，由其矩量母函数(moment generating function, MGF)可以推导得

EGi,zi{exp[-kqw(x)di-αGizi]e-η(βRi+p)+

1-e-η(βRi+p)}

(37)

因为Gi的概率分布为式(2)，利用伽马随机变量zi的矩量母函数，式(37)通过齐次泊松点过程的概率生成函数(PGFL)可以进一步推导得

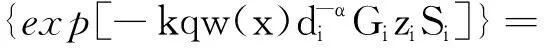
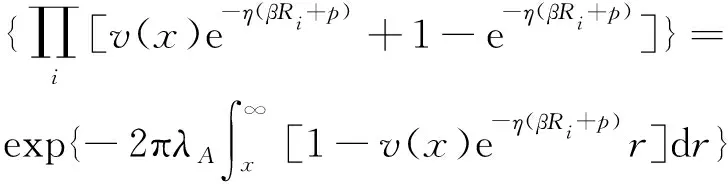
(38)

式(38)中：积分下限r是因为最近的干扰源位于距离用户r以外。将式(38)代入式(35)，可得到条件覆盖率的上限近似式(29)。

3 仿真验证

本节给出毫米波无人机网络在城市地区的覆盖率数值仿真结果，其中，数值结果通过理论公式计算得到，仿真结果通过蒙特卡洛法得到。未经说明时，系统参数默认设定如表1所示。

表1 仿真参数Table 1 Simulation parameters

图2为理论结果与仿真结果具有较好的近似效果。随着无人机装备的天线阵列阵子单元个数的增加，同一SIR门限T对应的用户的覆盖率也随之提升。这是由于无人机端天线阵列阵子数量的增加，使发送端的天线增益变大，接收端收到的有用信号总增益也随之增大，虽然干扰无人机的信号增益也增大了，但是由于定向天线的主瓣宽度很窄且随机指向，由式(2)计算可知，当天线阵子数由4增加到32时，干扰无人机发送端与下行用户接收端的主瓣波束对齐的概率由5.8×10-3减小到7.2×10-4，因此，干扰增益对用户覆盖率性能的影响远远小于有用信号增益的。此外，从图2可以看出，当SIR的门限T取值为0 dB时，不同天线阵子数量下的覆盖率都接近1，这说明对服务质量要求较低的地区(即较低的SIR阈值)，可以减少部署在该地区的无人机的天线阵子数量，这样可以在不影响系统性能的情况下，降低运营商成本。而当SIR的阈值等于10 dB时，不同天线阵子数量对应的覆盖率表现出明显差异，天线阵子数为4和8的系统，对应的覆盖率只有0.6和0.8，所以为了满足服务质量要求较高的地区，无人机携带天线的天线阵子数量应该不小于16。

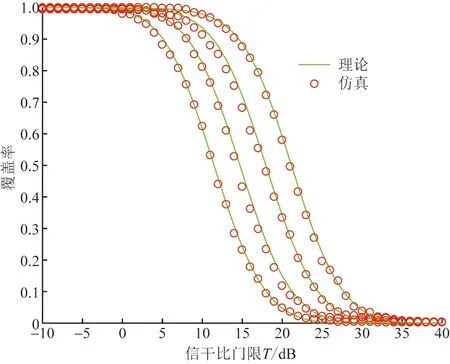
图2 不同天线阵子数量的覆盖率Fig.2 The coverage probability for different number of antenna elements

图3显示了在建筑物密集地区，覆盖率与无人机高度之间的关系。给定信干比门限T=20 dB，λB=6×10-4m-2，E[L]=E[W]=30 m，NA=16。

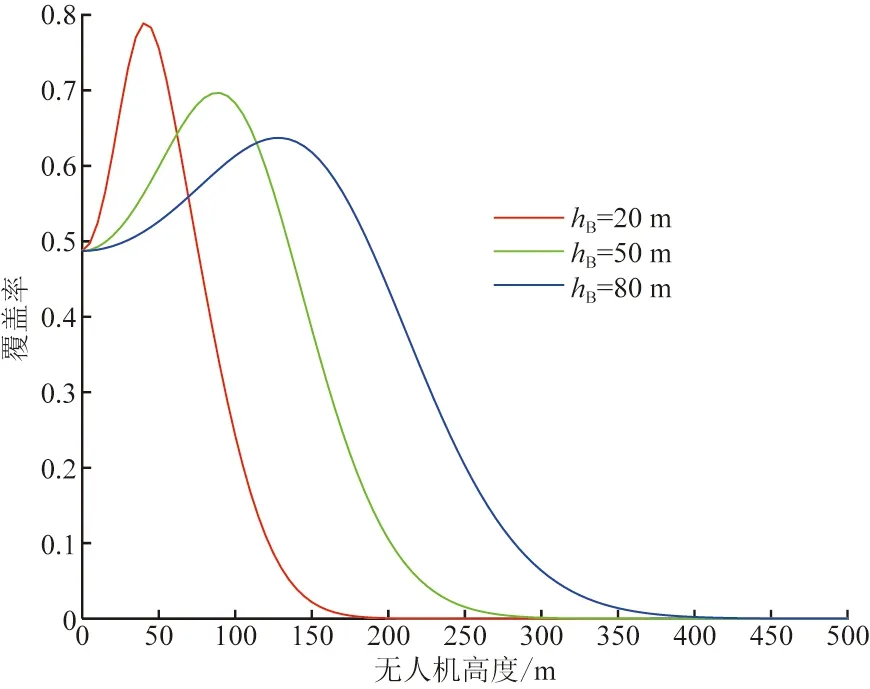
图3 无人机高度对覆盖率的影响Fig.3 The impact of the height of UAVs on the coverage probability

由图3可以得出以下结论。

(1)优化无人机高度可以提升系统性能。对于图3中任一曲线，当建筑物的平均高度固定时，用户的覆盖率先是随着无人机部署高度的增加而上升，达到一个峰值后，然后开始下降。这说明存在一个无人机部署的最优高度可以使覆盖率最大。这是因为在城市建筑物密集的地区，无人机平面的高度越高，与用户建立视距通信链路的概率也越高，所以开始的时候系统性能也随之提高。然而，当无人机达到一定高度后，路径损耗就成为影响网络性能的主要因素，随着无人机和用户之间距离的增加，覆盖率开始下降。

(2)用户覆盖率的峰值随着建筑物平均高度的增加而降低。这与建筑物越高，越容易对毫米波链路造成遮挡的事实相一致。

(3)针对上述环境，在建筑物比较低的区域内(即hB=20 m)，无人机部署在50 m左右时可以使系统覆盖率最大化，而在建筑物比较高的高楼区域(即hB=80 m)，无人机需要部署在140 m左右才能使达到最大覆盖率，且此时的覆盖率远小于前者。这是由毫米波的高路损特性决定的。

覆盖率与无人机密度之间的关系如图4所示。

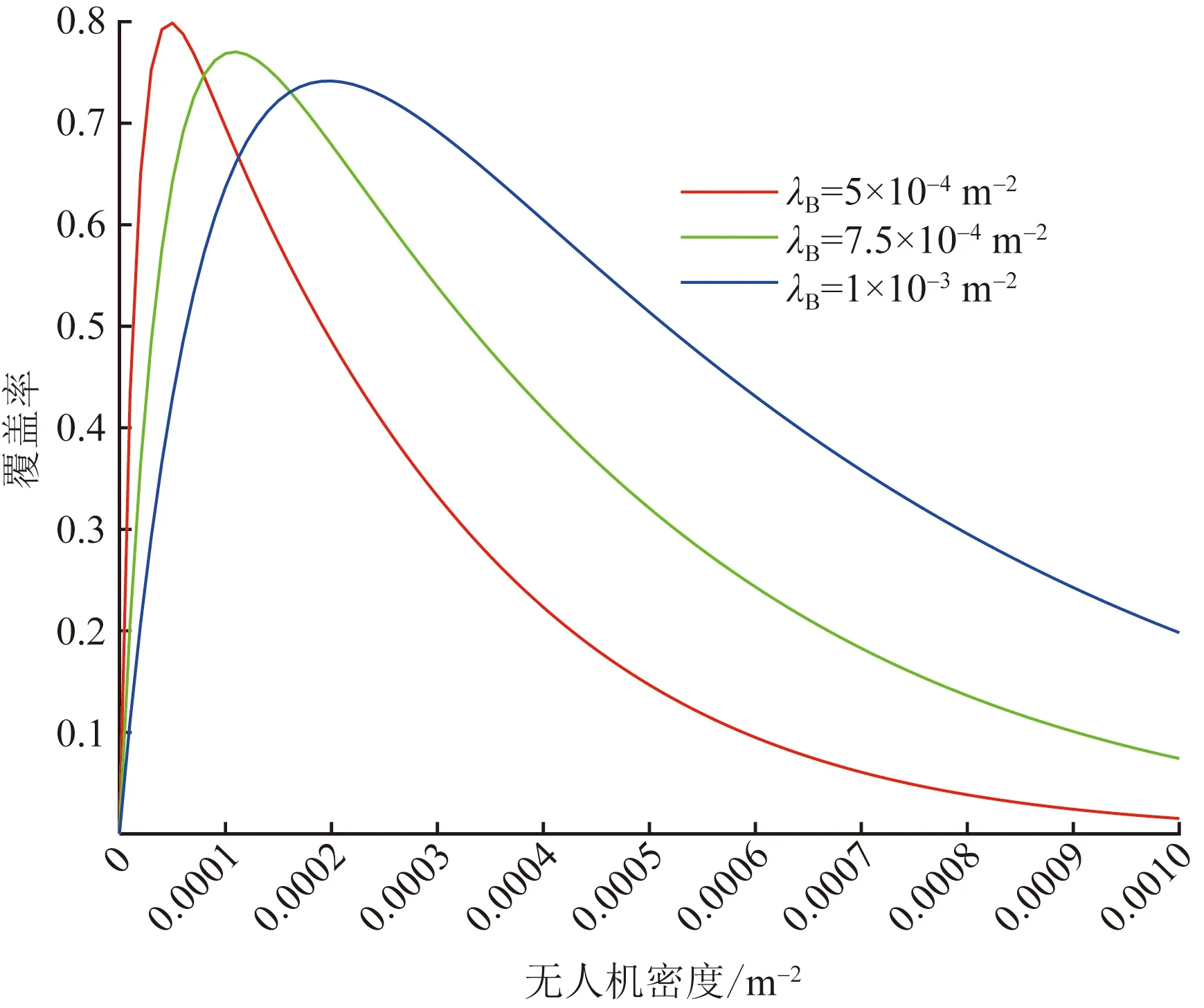
图4 无人机密度对覆盖率的影响Fig.4 The impact of the density of UAVs on the coverage probability

给定信干比门限T=20 dB，E[L]=E[W]=30 m，NA=16，hA=50 m。

由图4可以得出以下结论。

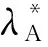
(2)随着无人机密度增大，开始时建筑物密度越大，能达到的覆盖率越小，这是因为此时建筑物密度的增大，导致用户端与距离近的无人机间的通信链路更容易被遮挡，延长了有用信号的传输距离，导致覆盖率下降。而随着无人机密度增大，建筑物密度和覆盖率的关系也随之变化，到了特定阈值后，建筑物密度越大，覆盖率也越大，这是因为当无人机密度足够大时，建筑物遮挡住距离用户近的无人机的概率降低，对有用信号传输距离的影响也随之减小，而距离相对较远的干扰信号仍会被建筑物遮挡，建筑物对干扰信号的抑制作用大于对有用信号的抑制作用，所以覆盖率随着建筑物密度的增大而升高。

(4)针对同一建筑物密度的条件下，无人机达到最优部署密度后，系统覆盖率将随着无人机密度的增大而迅速降低，这是由无人机的干扰信号导致的。在实际部署时需引入干扰协调等策略来降低干扰，保证用户接收到的服务质量。