多角色优化策略的灰狼-共生生物搜索算法

敖 山，彭雄飞，刘志中

1(河南理工大学 计算机科学与技术学院，河南 焦作 454003)

2(北京大学 教育经济研究所，北京 100871)

1 引 言

优化问题是指在满足一定条件下，在解空间中寻找满足条件的最优解或较优解，以解决实际应用需要的一类问题.优化问题已被应用于信号处理、图像处理、生产调度、结构设计、车辆寻径、任务分配、模式识别、等领域[1].鉴于各领域实际工程问题的复杂性、非线性、约束性以及建模困难等诸多特点，寻求高效的优化算法已成为必不可少且具有挑战性的研究领域.

由于科学中优化问题的重要性，已创建了许多算法和方法来处理此问题.传统的优化方法通常有严密的数理证明，如牛顿法、梯度法、单纯形法等.但随着优化问题规模的增大，这类传统算法无法在短时间内完成搜索，尤其是对于以复杂多峰函数位代表的非凸优化问题，传统优化算法理论基础的潜在缺陷是难以克服的.因此，现阶段的研究人员热衷于探索不使用任何梯度信息，且易于实现的新型优化算法，元启发式中的智能优化算法就是其中的代表.

智能优化算法大多受人类智能、生物群体的社会性行为及自然现象规律的启发[2]，其搜索模式源自生态系统中生物的行为或相互作用，且通常具有随机性、通用性、可并行处理等特性，这类算法无法确保所有问题都能找到令人满意的解决方案，但它们通常以最少的计算量即可产生最优解或较优解.这类算法的示例包括：遗传算法[3]、免疫算法[4]、差分进化算法[5]、粒子群算法[6]、人工蜂群算法[7]、灰狼优化算法[8]、共生生物搜索算法[9]等.另外，还已有研究者开发了现有优化算法的各种改进和优化版本以及两种或更多种优化算法的混合版本.

其中，共生生物搜索算法[9](SOS)是近几年提出的，一种模拟生态系统中生物互利共生、偏利共生、寄生等行为的新型智能优化算法.其优点在于，需给定的控制参数仅2个，使其具有较高的通用性，且收敛速度与精度较高，尤其在单峰优化问题的计算中优势明显.由于这个原因，SOS自提出以来，已在各类实际问题中均有应用，如项目调度[10]、车辆路线[11]、电力系统[12]、多目标约束问题优化[13]等.但标准SOS算法的设计也存在一定缺陷，如在高维多峰优化问题中易陷入局部最优、中后期收敛速度慢而易导致搜索停等.表明SOS算法具有强大的挖掘能力，但探索能力相对薄弱，导致在复杂优化问题中，算法可能实现全面的全局搜索.为了平衡这算法两种能力，使算法更好、更稳定，国内外研究者已开展各类研究以优化SOS算法的性能，如在原始SOS算法中引入自适应受益因子[14];进行反向学习，从而避免局部最优并加快了收敛速度[15];集成模拟退火算法而形成混合算法[16];结合自适应思想，利用不同差分扰动项和精英学习策略进行改进[17];结合子种群拉伸操作与精英级制以平衡探索能力与挖掘能力[18]等.

本研究针对SOS的上述特性，受该领域已有研究成果的启发，提出一种基于多角色优化策略的混合灰狼-共生生物搜索算法(Multi Role Optimization Strategic Grey Wolf Optimizer-Symbiotic Organisms Search Algorithm，MRSSOS).该算法分别从算法的内部结构、扰动机制及算法混合方面进行了优化，结果表明本研究提出的算法性能明显较好，在大部分优化问题中，均可在极少的迭代次数中获得较高的搜索精度，尤其在多峰问题的处理方面优化明显，表明MRSSOS很好地平衡了算法的探索能力与挖掘能力，具有较好的跳出局部最优的能力.

2 基本SOS算法的原理

SOS算法是一种近几年在国际范围内被广泛应用于各类优化问题的元启发式算法，可基于自然生态系统中不同生物之间的共生关系(互利共生、偏利共生、寄生)来在解空间中进行随机搜索与局部搜索，以处理优化问题.这种算法对种群初始位置的依赖相对较小，算法中每个生物个体都具有适应度值并代表其对所考虑问题提供的解的效果.在每个迭代过程中，SOS算法对种群中的每个个体依次模拟自然界中的互利共生、偏利共生、寄生行为特征，进行种群进化，如果每个阶段的新个体的适应度值优于原个体，则对个体进行更新，直到迭代次数完成或精度满足停止标准为止.

2.1 互利共生操作

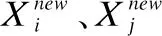
(1)

(2)

(3)

其中，rand(0，1)是一个维度与Xi、Xj相同，值为0-1之间随机数组成的向量;Xbest是当前种群的最优个体;MV表示一对互利共生关系的生物的共同载体;BF1、BF2是描述每种生物的收益水平的收益因素，通常取1或者2.

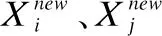
2.2 偏利共生操作

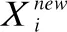
(4)

2.3 寄生操作

这个阶段描述了一种寄生关系，在这对关系中，一方受益，另一方受害，后者为前者提供生存场所.自然界中例子如疟疾原虫与人类宿主之间的相互作用.寄生虫通过蚊虫叮咬转移到人类宿主.感染后，该寄生虫生长，繁殖并侵入红细胞，引起疟疾.如果宿主的免疫力足够强，它将消灭寄生虫.否则，人类可能患上疟疾并患上重病或死亡.

在这个阶段中，所操作的个体Xi中的若干位进行变异，产生寄生体Parasite_Vector，并在种群中随机选择一个相异的个体Xj作为宿主进行寄生，即将两个体的适应度进行比较，如果Parasite_Vector具有更好的适应度值，则将Xj淘汰，并用Parasite_Vector进行替换.

3 本研究提出的MRSSOS算法

3.1 改进思路

先前研究成果表明，群智能优化算法改进的思路可分为4类：1)通过改善内部结构，增加种群多样性保持机制[19]，寻找探索能力与挖掘能力的新平衡;2)通过设计自适应算子[20]，以减少预设参数的个数，并提高算法的通用性;3)通过增加停滞防止机制及扰动机制[21]，避免算法早熟或陷入局部最优，提升局部搜索能力;4)设计混合智能优化算法[22]，将两种或多种算法结合起来，扬长避短，提升整体性能.

通过深入思考SOS性能瓶颈的根源，进行大量实验研究，针对SOS算法存在的易陷入局部最优及搜索停滞等缺陷与复杂多峰函数表现不佳等情况，本研究从集成灰狼优化算法狩猎算子、算法进化阶段的多角色策略改良、增加陷入搜索停滞后的扰动机制3个方面进行改进，并提出一种多角色优化策略的灰狼-共生生物搜索算法(MRSSOS)，主要改进包括：首先，在每轮迭代的开始引入改进后的灰狼优化算法狩猎算子，按由适应度与相似度构成的激励度的高低，选出种群中的头狼，即激励度最高的3个解，并根据3只头狼的位置更新整个种群中每个个体的位置.既使种群向最优解方向靠拢，又保持一定的多样性;其次，在“互利共生”阶段，根据处理的点的适应度，将种群分为两段，并各抽取一个个体，分别赋予探索者与开发者角色，各自分工不同：探索者同时具备社会性运动趋势与惯性运动趋势，运动目的是收敛的同时保护种群多样性;开发者仅具备社会性特征，从自身所处位置向种群最优解移动，专注于提升种群挖掘能力.在“偏利共生”阶段，同样进行探索者与开发者的角色分工，并借鉴差分进化思想，将两种角色的搜索“经验”传递给所操作的点，并引入扰动算子，使两种角色不过于偏离种群整体中心.最后，在寄生阶段，采用精英机制，由精英个体变异产生寄生体，寄生于所操作的点，使精英的挖掘能力得以显著增幅，从而在搜索的中后期提升深度搜索能力，避免搜索停滞.最后，在种群搜索陷入停滞时，设计了种群刷新机制，将种群随机分为3段，分别进行复制变异、倒转镜像、中心刷新等操作，从而使种群恢复搜索能力.下面对改进部分进行详细介绍.

3.2 改进的灰狼优化算法狩猎算子

在传统的SOS算法中，各进化阶段仅受个体值及一个最优解值的影响，若当前最优解是局部最优解，则整个搜索过程中，易使整个种群共同陷入局部最优，造成早熟.针对这个情况，本研究集成了灰狼优化算法的阶级制度与狩猎算子.灰狼优化算法(Grey Wolf Optimizer，GWO)是Mirjalili 等人于2014年提出的一种新型群智能优化算法[23].思路来源于自然生态系统中灰狼群体的捕食行为，及狼群内部严格的支配等级关系.在使用狩猎算子之前，首先需模拟自然界中狼群的行为组织模式，对头狼α、β及γ进行更新.在本算法中，该算子的设计目的在于保持种群多样性、避免早熟的同时，向最佳位置逼近，因此更新头狼的方式不仅依靠适应度，而是根据下式计算个体的激励度urge(Xi)，其中Xj∈(α，β，γ)：

urge(Xi)=-fitness(Xi)+sim(Xi，Xj)

(5)

(6)

fitness(Xi)表示个体Xi的适应度值，对每个个体Xi，若其适应度优于当前的头狼，则计算激励度，激励度高则替换.头狼更新后，按下式进行狩猎：

A=2ar1-a

(7)

C=2r2

(8)

D=|CXP(t)-X(t)|

(9)

X(t)=XP(t)-AD

(10)

(11)

(12)

X(t+1)=(X1+X2+X3)/3

(13)

引入GWO算法的狩猎算子，可从一定程度上避免SOS本身算法结构导致的种群趋同性，在保持多样性的同时也保持了一定的搜索精度.

3.3 多角色优化策略

传统SOS算法的进化过程中，所操作的每一个体都有快速逼近种群最优解的趋势，导致算法虽然有较好的挖掘能力，但探索能力较多，算法对解空间的全局搜索不够充分是算法陷入局部最优、搜索停滞现象的主要原因.因此，为了有效平衡算法的探索能力与挖掘能力，可通过对种群中的个体赋予不同的角色并进行相应的进化操作.

主要做法是根据个体适应度的高低，赋予探索者与挖掘者的角色，探索者的任务是勘探整个解空间以寻找可能存在最优解的区域，重点强化其与其他非最优解个体间的沟通能力;挖掘者的任务是面向当前发现的较好的区域，进行局部挖掘，寻找更优解，重点强化其与最优解的沟通能力.在这个策略下，种群当前最优解由挖掘者群体维护并更新，探索者群体负责全局搜索且不会影响最优解的精度.在算法的探索能力与挖掘能力间寻找了共存的方式.

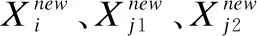
(14)

(15)

其中，r是一个0-1之间的随机数，根据数值大小进行不同的进化操作，BF1、BF2是描述每种生物的收益水平的收益因素，通常取1或者2.

挖掘者Xj1主要与最优值进行沟通，并围绕最优值附近进行局部搜索：

(16)

探索者主要保持自身惯性，并与Xi进行沟通，从而实现全局搜索：

(17)

(18)

在偏利共生阶段，传统SOS算法的式(4)直接根据随机获取的个体Xj对Xi进行更新，存在两个缺陷：1)随机获取的点Xj在后期往往无法对Xi进行更新，导致搜索停滞;2)该阶段的搜索模式与上一阶段大体相似，社会部分与种群中其他个体的沟通信息量不足，导致Xbest在其中影响力过大，从而易陷入局部最优.因此，同样基于多角色优化策略，抽取挖掘者Xj1与探索者Xj2，进行多策略的偏利共生：

(19)

(20)

其中，fitnessave是整个种群适应度的均值，引入kj*表示个体Xj*与种群中心的偏离度，从而提高算法的收敛速度.在这个进化策略中，如果Xj1、Xj2相对较优，则直接根据公式更新Xi，但如果在后期面临搜索停滞或陷入局部最优局面时，通过获取更多的种群社会信息，可在合理的范围内提供扰动机制，从而跳出最优并更新个体于一个可能存在最优解的区间，因此可实现自适应不同情形的探索能力与挖掘能力的有效平衡.

在寄生阶段，传统算法的策略是将操作的个体变异后生成寄生体，存在两个缺陷：1)若个体Xi性能不佳，变异后无法对Xj进行更新，导致无效搜索，从而有可能使算法陷入搜索停滞状态;2)在这个阶段中，有可能对同一个Xj多次进行更新，浪费算力，且不利于保持种群的多样性.因此，基于多角色优化策略进行改进，对于每一个操作的个体Xi，从适应度高于Xi的挖掘者群体中选择一个Xj，变异后对Xi进行更新，以保证每次更新都可以将挖掘者的历史经验传递给Xi，从而提高收敛速度.

3.4 陷入搜索停滞后的扰动机制

实验数据表明，上述两个改进显著提升了SOS算法的收敛速度，通常在200次迭代左右，群体中的几乎所有个体将集中在某一点周围，即获得一个较优解(如图1所示)，但精度仍有提高空间，且依然有概率陷入搜索停滞期.因此，针对这种情况，增加陷入搜索停滞后的扰动机制，增强算法的种群多样性，避免算法发生早熟收敛现象，提高算法的全局搜索能力与寻优能力.

图1 种群收敛过程示意图

由于单一策略难以应对复杂多样的情况，因此采用3种扰动机制形成复合策略，并对种群中的每个个体随机使用其中一种，从而保证扰动机制在大多数情况下均是有效的.结合算法机制与实验结果，设置的3种扰动机制分别为复制变异、倒转镜像、中心刷新.

复制变异是选择个体Xi中的2个随机不同的位置，将其中一个的值复制到另一个，生成的两个变异体与原始个体的适应度进行比较，保留适应度较高的个体，如图2所示.

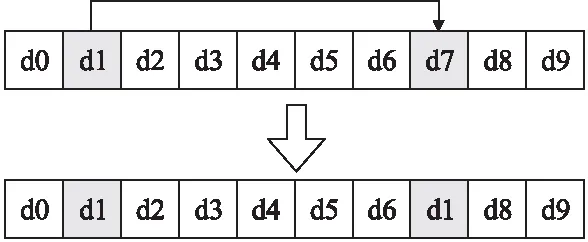
图2 d1号位与d7号位进行复制变异操作

倒转镜像变异是随机选择个体Xi中的一个位置dk与一个随机长度l，以dk为中心对两侧l长度内的值进行镜像操作，如图3所示.

图3 d3号位为中心，长度为1进行倒转镜像操作

中心刷新是将选择个体Xi中每一个位置的值，都刷新为每一个位置值均值附近符合柯西分布的随机值.从而使个体Xi刷新并在可能产生最优解的区间内生成一个新的值.

这3种扰动机制的综合使用，可使种群在陷入搜索停滞时，产生强有力的变异，从而跳出局部最优，并恢复搜索能力.且与完全随机扰动、变异机制相比，这种复合扰动机制可将扰动的范围收缩在合理的区间内，既不会使扰动失效，又不会完全抛弃先前搜索的历史经验，因此可取得较好的效果.

3.5 算法执行流程

本研究设计的MRSSOS算法实现具体流程图如图4所示.

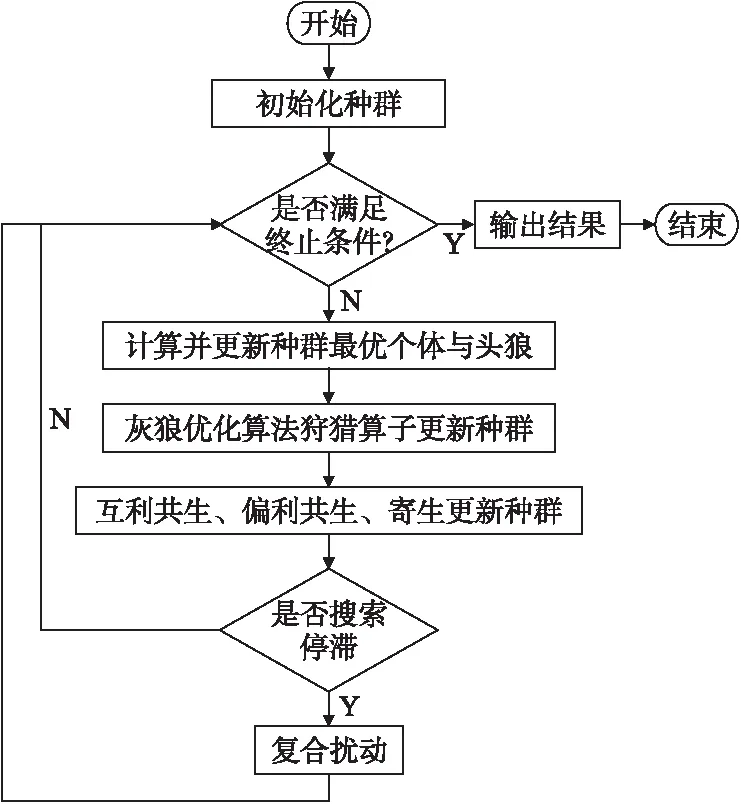
图4 MRSSOS算法流程图

4 实验结果与分析

为了充分验证本研究设计的MRSSOS算法在求解优化问题时有效性，本研究进行了一系列实验，实验所用的计算机配置如下：CPU：Intel(R)Xeon(R)E5-26900，主频2.90GHz，内存16G.编程语言为Python3.7.0.

4.1 函数说明与性能指标

为尽可能全面的评价算法的性能，本研究选取了19个国际通用的表准测试函数进行测试，其中，F1-F10为单峰函数，F11-F19为多峰函数(如表1所示).其中，单峰函数主要用来验证算法的收敛能力与求解精度.多峰函数具有大量局部最优解陷阱，用以评估算法跳出局部最优的能力，及全局搜索的能力.

表1 标准测试函数表

评价指标方面，本研究选用收敛速度、求解精度、稳定性3项作为评价指标.其中，收敛速度指迭代序列向最优值或较优区间逼近的能力，以相关算法在搜索过程中的收敛曲线进行评估;求解精度指的是算法结果的准确度，相关算法在给定实验环境下计算结果的平均值与函数理论最优值差距越小，精度越高;稳定性可反映算法的全局搜索能力与避免陷入局部最优的成功率，指算法每次运行得到的计算结果是否会产生较大波动，相关算法在给定实验环境下计算结果的标准差越小，稳定性越高.

4.2 与同系列算法比较

为评估本研究提出的算法改进是否对SOS算法的性能进行有效的提升，首先将MRSSOS与同系列目前较新、改进性能较好的其他算法进行比较.通过查阅文献，选择标准SOS以及QOCSOS及SPS-SOS作为对比算法.QOCSOS算法是2019年Khoa H.Truong等提出的将基于拟对位的学习和混沌局部搜索策略与SOS集成在一起的SOS改进算法[23];SPS-SOS由王艳娇等于2019年提出，采取精英机制并引入拉伸因子和差分扰动向量，并取得了较好的求解精度[18].参数设置方面，为体现公平性及对比参照性，种群规模统一设置为30，维度为30，最大迭代次数1000次，其他参数均为对比算法原文献设置值.对每个测试基准函数，各算法独立运行30次，并求其最终解的平均值与标准差，用以评估算法的求解精度、收敛速度、稳定性.具体实验结果如表2所示.

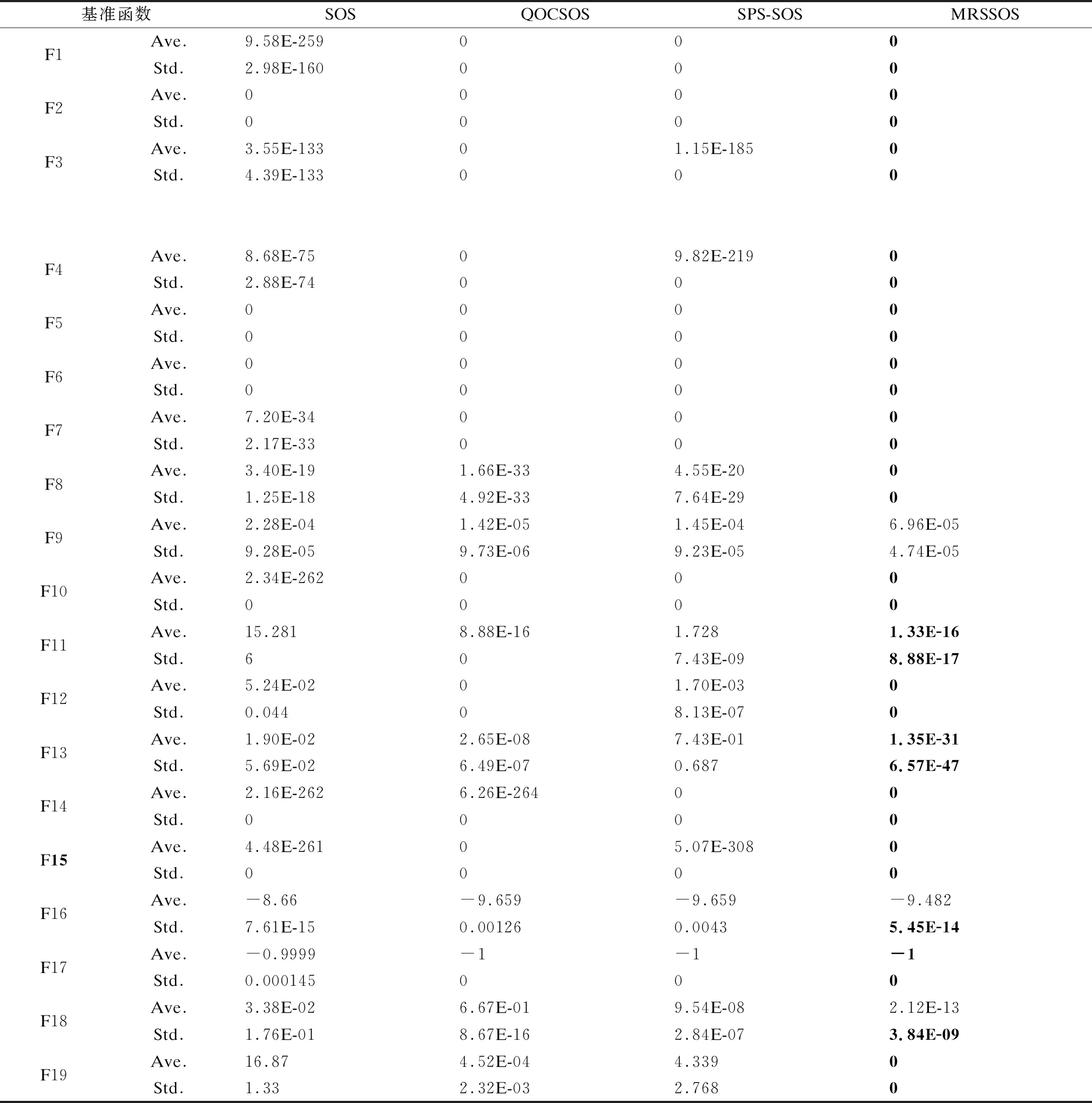
表2 同类别算法性能对比测试结果统计

通过分析实验结果，可以看出，对于实验选择的F1-F10的单峰函数，MRSSOS基本可以在极少的迭代次数内收敛到最优，且非常稳定.而其他算法中，QOCSOS可将7个基准函数收敛到最优，SPS-SOS是6个.因此本研究提出的算法在收敛速度与精度方面具有明显的优势.

复杂多峰函数方面，F11-F19的9个基准函数中，MRSSOS可将5个收敛到理论最优值，其他4个中，有2个的计算结果优于对比算法.说明本研究提出的MRSSOS算法的求解精度明显优于其他对比算法，提出的改进方案有效的平衡了算法的探索能力与挖掘能力.同时，表中还可以看出，MRSSOS的标准差均小于其他算法，且算法性能在高维函数问题中，下降并不明显，表示该算法更为稳定与通用，体现了多角色优化策略在处理各类情况时的全面性.

综上所述，与SOS、QOCSOS、SPS-SOS等同系列算法相比，本研究提出的MRSSOS算法具备更好的求解精度以及稳定性.

4.3 与其他仿生优化算法比较

为了充分验证MRSSOS算法的性能优越性，通过查阅资料，考虑到MRSSOS“分角色”的概念特征以及对灰狼算法狩猎算子的集成，选择了3种目前优化效果较好且与MRSSOS算法有一定相关性的3种算法进行对比实验，包括一种带变异算子的自适应惯性权重二进制粒子群优化算法(MABPSO)[24]、一种基于自适应随机优化策略的人工蜂群改进算法(SRABC)[25]，以及通过对种群初始化进行策略设置以提高种群多样性，并以非线性调整策略来增强算法的搜索能力的SFL-GWO算法[26]作为对比目标，从求解精度及稳定性方面进行综合比较.

出于公平性考虑，各算法的种群规模都为30，维度为30，最大迭代次数为1000，参数按原作者期刊中的描述进行设置.基准函数选择了3个典型的单峰函数F1、F8、F10以及两个多峰函数F11、F12.具体实验结果如表3所示.结果表明，与MABPSO、SRABC、SFL-GWO等目前优化效果较好的仿生优化算法比较，本研究提出的MRSSOS算法具备更好的求解精度以及稳定性.

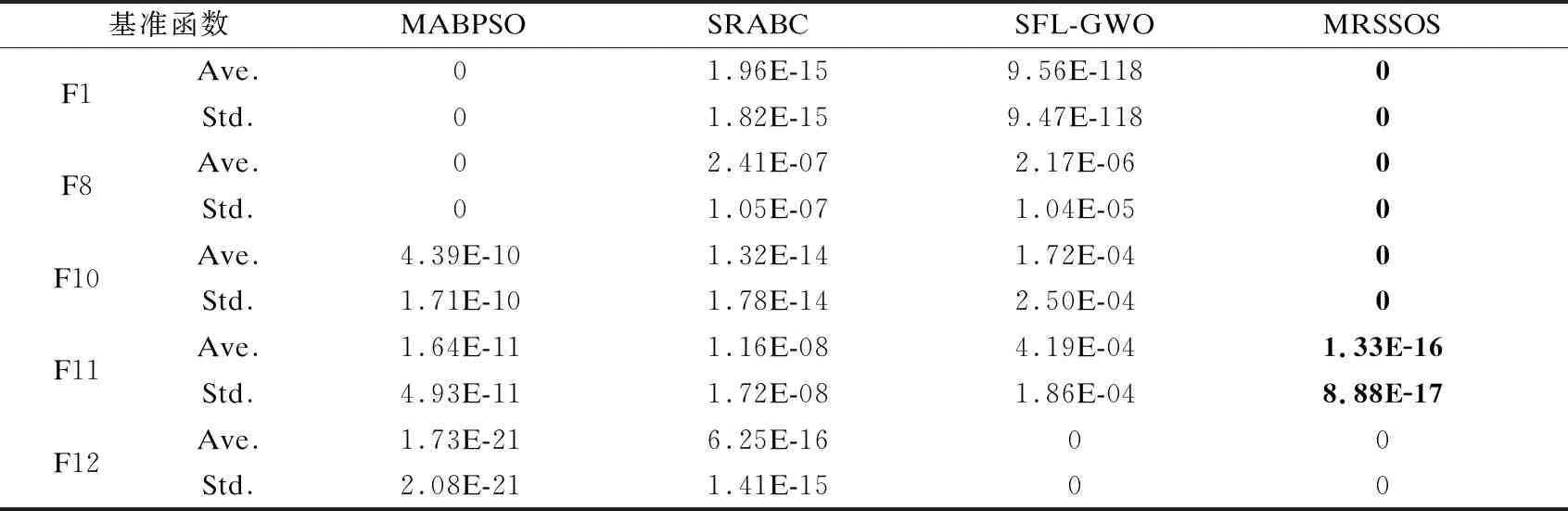
表3 不同类别算法性能对比测试结果统计

4.4 收敛速度比较

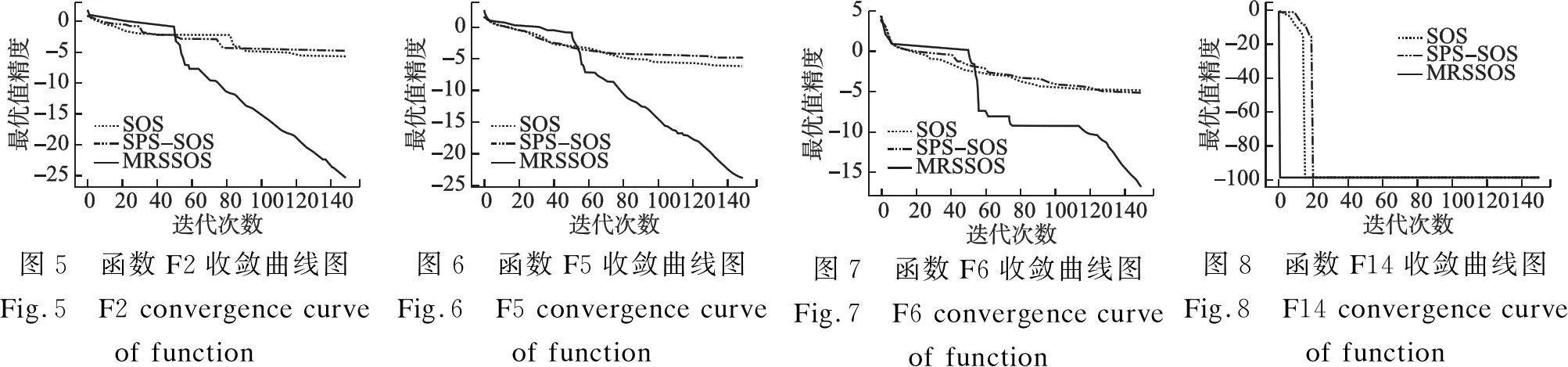
为考察本研究提出的MRSSOS算法的收敛速度，针对SOS、SPS-SOS及MRSSOS均获得较高求解精度的单峰函数F2、F5、F6以及多峰函数F14，绘制3种算法的收敛曲线，参数设置与上文保持一致.结果如图5-图8所示，为更直观显示3种算法的收敛速度，x轴表示迭代次数，y轴对算法的最优值取对数，以显示最优值精度，且仅显示前150次迭代的结果.

从收敛曲线可以直观看出，本研究提出的MRSSOS在初始阶段更重视全局搜索能力，从而在后续迭代过程中获得更强大的收敛能力，即在全局探索和局部挖掘能力之间取得了一个较好的平衡，且收敛速度及精度明显优于其他两种算法.此外，图中也可以看出，由于复合扰动机制的存在，MRSSOS算法在陷入局部最优解时，可以更容易的恢复收敛能力.总体而言，MRSSOS在收敛速度方面有较大的优势.

5 结 论

本研究针对标准SOS算法中存在的易陷入局部最优及搜索停滞等缺陷，基于多角色复合策略进行了一系列改进，并在原先迭代过程中集成灰狼优化算法的狩猎算子，提出了一种基于多角色优化策略的灰狼-共生生物搜索算法(MRSSOS).首先，在每轮迭代的开始引入改进后的灰狼优化算法狩猎算子，既使种群向最优解方向靠拢，又保持一定的多样性;其次，在共生搜索时，同时抽取探索者与开发者角色进行协作，在种群探索能力与挖掘能力中寻找了最佳平衡.最后，在种群搜索陷入停滞时，设计了种群刷新机制，将种群随机分为3段，分别进行复制变异、倒转镜像、中心刷新等操作，从而使种群恢复搜索能力.结果表明，改进后的MRSSOS算法性能明显更好，在大部分优化问题中，均可在极少的迭代次数中获得较高的搜索精度，尤其在多峰问题的处理方面优化明显，表明MRSSOS在全局搜索能力、收敛速度、求解精度、稳定性方面性能都具有一定优势.下一步的研究重点一方面是将本研究算法应用于任务调度、结构设计等实际应用中;另一方面是继续优化算法结构，降低算法复杂度，从而使算法在高维问题中具备更高的通用性.