曲线系与斜率关系的探讨应用——定点定值一类问题的探究

陈 春

圆锥曲线中的定点定值问题不仅是一个考查学生基本功的问题,也是对学生在化归思想应用上的一个考查。通性通法可以帮学生逐步化简求解相应问题,但其中所包含的计算相对烦琐,对运算能力不强的同学,这类问题往往会成为解题路上的拦路虎。如果我们转换思维灵活的利用点线关系,借助曲线系方程来求解这类问题,那么学生就能很快地解决这类问题。

【结论1】

已知直线l1:A1x+B1y+C1=0 与直线l2:A2x+B2y+C2=0,则方程(A1x+B1y+C1)(A2x+B2y+C2)=0 可以表示这两条直线,而展开后是一个二次方程形式,这个方程可以理解为一个曲线Γ。

【结论2】

若过圆锥曲线C上一点P(x0,y0)处的两条直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,与圆锥曲线C交于A,B两点,且kPA+kPB或kPA·kPB为定值,则直线AB必过定点。反之,若直线AB过定点,则kPA+kPB或kPA·kPB为定值。

分析:过点E的两条直线EA,EB的斜率之积为-1,可设直线EA,EB的方程,借助曲线系方程思想,找出椭圆与新曲线的交点P,M所在直线PM,进而解出直线l的斜率。

解析:设直线EA,EB的方程分别为t1x -y -1=0,t2x -y -1=0 且t1t2=-1.

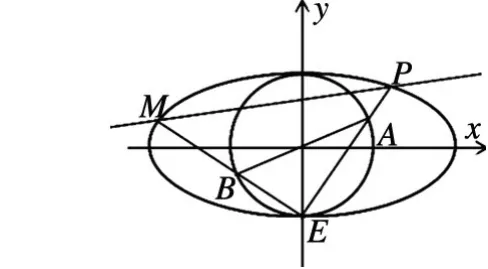
则可得二次曲线Γ:(t1x -y -1)(t2x -y -1)=0,即t1t2x2-(t1+t2)x(y +1)+(y +1)2=0.

∵y≠-1,且x2=2(1-y2)

∴ (t1+t2)x -3y +1=0 即是椭圆C1与二次曲线Γ的交线

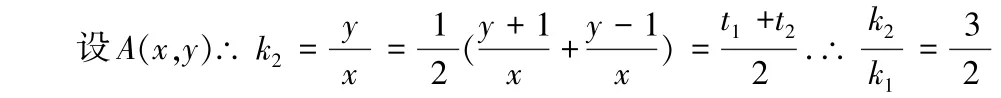
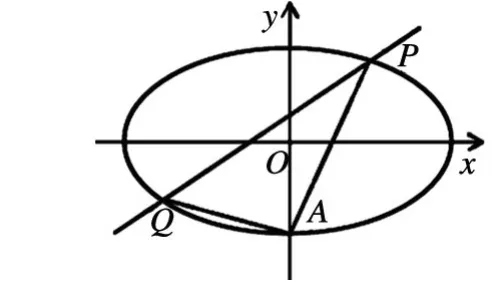
分析:点(1,1)可以理解为直线所经过的定点,利用结论2 的逆向结论,就可以直接求解。

解析:设直线AP与AQ的分别方程为k1x -y -1=0,k2x -y-1=0.

可得到二次曲线Γ:(k1x -y -1)(k2x -y -1)=0,即k1k2x2-(k1+k2)x(y +1)+(y +1)2=0.

∵y≠-1,且x2=2(1-y2)

∴2k1k2(1-y)-(k1+k2)x+y +1=0 即是椭圆E与二次曲线Γ的交线PQ,

又PQ过点(1,1),则k1+k2=2.

例3、(2020 年全国理20 题)已知A,B分别为椭圆=1(a＞1)的左、右顶点,G为E的上顶点,为直线x=6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

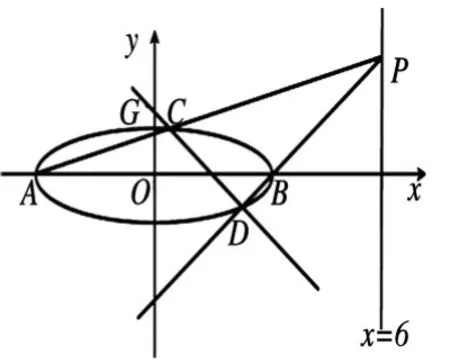
(1)求E的方程;

(2)证明:直线CD过定点.

上述几个问题都是利用曲线系的引入来求解问题的,联立圆锥曲线方程时要注意条件的使用,如例3 中“x≠3” 原因是什么。这种求解可以让很多学生跳过必须使用韦达定理的思维误区,要让学生在解决这种问题的同时思考这样做的本质是什么,解析几何的实质是什么。

利用这种方法我们不但可以让学生多掌握一种解决问题的方法,也能让学生站在更高的角度思考问题,从而提升学生对解析几何认知水平,进而发展学生的解题思维。