具有控制结构的集值强向量均衡问题解集的本质连通区
2021-11-21赖遵远陈剑尘
赖遵远,陈剑尘
(南昌航空大学,数学与信息科学学院,南昌 330063)
引 言
在研究非线性问题的稳定性中,解集的本质连通区的存在性是值得探讨的问题。而强向量均衡问题求出的强解是一种理想的解,相比向量均衡问题中的有效解、弱有效解和真有效解等均更好[1-6]。因此,研究强向量均衡问题解集的本质连通区是十分有意义的,同时也取得了一些相关研究成果。例如:龚循华和袁淑敏[7]在约束集值映射满足一定连续性、目标映射是锥-真拟凸的条件下,证明了对称强向量拟均衡问题构成的空间M中其解集的本质连通区的存在性定理;孟旭东和张传美[8]在目标映射为锥-真拟凸、约束集值映射满足一定连续性的条件下,得到了广义强向量拟均衡问题构成的空间M中对每个广义强向量拟均衡问题解集至少存在一个本质连通区;熊昀暄和陈剑尘[9]在序锥C的拓扑内部为空、C非空的条件下,给出了强向量均衡问题解集的本质连通区也是存在的结论。
一些数学家研究解集的本质连通区都是在序锥不变动的情况下进行的,而事实上当序锥变动时,解集的本质连通区也是值得研究的。本文在文献[10]的基础上,利用具有控制结构的集值强向量均衡问题解映射为usco映射的引理,当序锥是变动的以及映射满足一定的条件下,证明了具有控制结构的集值强向量均衡问题解集的本质连通区的存在性定理。
1 预备知识
除特别说明外,本文始终假设X和Y均为实Hausdorff拓扑线性空间,K是X中的非空紧凸子集,C:K→2Y是一个集值映射,使得对∀x∈K,C(x)均为Y中的闭凸点锥。族{C(x):x∈K}被称为Y上的控制结构[11],记K(Y)表示为Y上全体的非空紧子集。再设F:K×K→2Y为集值映射,我们考虑以下具有控制结构的集值强向量均衡问题(简称SSVEPD):求x∈K,使得
接下来,我们来介绍一些集值映射的基本概念和结论。
定义1.1[12]设X和Y均为拓扑线性空间,F:X→2Y为集值向量,则
(1)称F在x′∈X处是上半连续的,若对包含F(x)的任一开集V,存在包含x′的开集U,使得F(x)⊆V,∀x∈U. 称F在X上是上半连续的,若F在X上的任一点均为上半连续的。
(2)称F在x′∈X处是下半连续的,若对包含F(x)任一开集V,F(x′)∩V≠∅,存在包含x′的开集U,使得F(x)∩V≠∅,∀x∈U。称F在X上是下半连续的,若F在X上的任一点均为下半连续的。
(3)称F在X上是连续的,若F在X上既是上半连续的,又是下半连续的。
(4)称F是usco映射,若对任意的x′∈X,F(x′)是紧值的,且F在X上是上半连续的。
引理1.1[13]设E1和E2均为赋范线性空间,A⊂E1,B⊂E2均为非空紧凸集,T1:A→2B,T2:A→2B均为A上有非空紧凸值且上(下)半连续的映射,λ(x)和µ(x)均为A上的连续函数,且λ(x)≥0,µ(x)≥0,λ(x)+µ(x)=1,∀x∈A,则
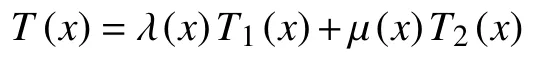
是A上 具有非空紧凸值且上(下)半连续的映射。
引理1.2[14]设D是一个半序集,如果D的每一个全序子集都有上(下)界,则D必有极大(小)元。
定义1.2[10]设X和Y均为拓扑线性空间,C:K→2Y是一个集值映射,使得对∀x∈K,C(x)均为Y中的闭凸点锥。G:X→2Y为集值映射,称G为C(x)−似拟凸的,若对∀x1,x2∈X,∀λ∈(0,1),有
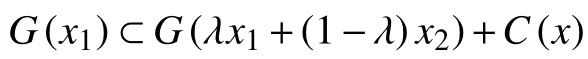
或者

文献[10]给出了具有控制结构的集值强向量均衡问题解的存在性定理。
引理1.3[10]设X和Y均为实Hausdorff拓扑线性空间,K⊂X为非空紧凸子集,C:K→2Y为闭集值映射,C(x)为Y中的闭凸点锥,F:K×K→2Y为集值映射。如果下列条件同时成立:
(1)对∀x∈K,F(x,x)⊂C(x);
(2 )对∀y∈K,F(x,y)在K上关于x是下半连续的;
(3)对∀x∈K,F(x,y)在K上关于y是C(x)−似拟凸的。则
(i )SSVEPD在K中是可解的,即存在x∈K,使得
(ii)SSVEPD解集是K中的紧子集。
2 SSVEPD解集的本质连通区
在本节中,将证明对任一u=F∈M,Φ(u)中都至少存在一个本质连通区。设X和Y均为Banach空间,K为X中的非空紧凸子集,F:K×K→2Y为集值映射。令
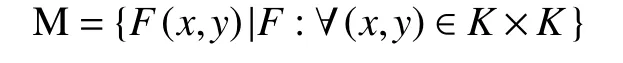
其中,F(x,y)是紧值,且满足引理1.3中(i)、(ii)、(iii)。
设B1和B2均为赋范空间中的紧子集,则B1和B2中的Hausdorff度量定义为:

其中,h0(B1,B2)=sup{d(b,B2)|b∈B1},d(b,B2)=inf{|b−b′||b′∈B2}。
对∀F1,F2∈M,定义:
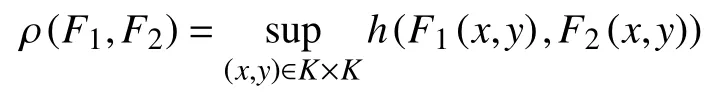
其中,h表示为K(Y)上的Hausdorff度量,K(Y)表示为Y上的所有非空紧子集。
于是对 ∀F∈M,Φ定义了一个从M到2K的集值映射且Φ(F)≠∅。
引理2.1[10]Φ:M→2K是一个usco映射。
定义2.1[10]对任意的u=F∈M,x∈Φ(u),则
(1)称x是Φ(u)的本质解,如果对x在K中的任何开邻域O,存在u在M中的开邻域V,使得对∀u′∈V,有Φ(u′)∩O≠∅。
(2 )称u是本质的,如果u的任一解均为本质的。
(3)称u是弱本质的,如果存在u的 某个解为本质的。
引理2.2[10]存在M中的稠密剩余集Q,使得对∀F∈Q均 为本质的。
下面的例子类似于文献[15]中的例1。
例1令F(x,y)={(x1,y1),(x2,y2)},∀(x,y)∈K×K,其中(x1,y1)≠(x2,y2). 显然F∈M,Φ(F)={(x1,y1),(x2,y2)}.如果 Φ(F)存在本质解,则本质解只能为x1或x2。
下证x1或x2均不可能为Φ(F)的本质解。
不妨设x2是Φ(F)的本质解,那么由于(x1,y1)≠(x2,y2),故存在ε0>0,使得
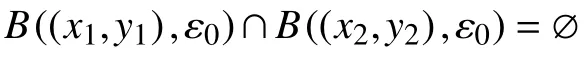
其中,B((xi,yi),ε0)={(x,y)∈K×K|h((x,y),(xi,yi))<ε0},i=1,2。
于是,对∀ε∈(0,ε0),显然B((x2,y2),ε)为(x2,y2)的一个开邻域。但对∀δ>0,我们取∈M满足存在(x0,y0)∈K×K,使得

上述例子表明,引理2.2中的Q≠M,即M中的某些问题甚至不存在本质解,因而有必要研究M中问题的解集的本质连通区。
设u=F=M,x∈Φ(u),则称Φ(u)中包含x的所有连通子集的一个并集为x∈Φ(u)的连通分支[16]。因为K为紧的以及连通分支是Φ(u)的连通闭子集,所以连通分支是连通紧集,且Φ(u)有以下的分解:,其中Λ为指标集。
对∀α∈Λ,Φα(u)是Φ(u)中的非空连通子集,且对∀α∈Λ,∀β∈Λ(α≠β),有Φα(u)∩Φβ(u)≠∅
引理2.3[17]设A,B和W均为K中的非空有界集,则

其中h为 Hausdorff度量,λ≥0,µ≥0且λ+µ=1。
定义2.2[13]设u=F∈M,P是Φ(u)中的非空闭子集。
(1)称P是Φ(u)的本质集,若对包含P的任意一个开邻域O,存在δ>0,使得对∀u′∈M且ρ(u,u′)<δ,有
(2)称Φ(u)中的连通分支Φα(u)是一个本质连通区,若Φα(u)是本质的。
(3)称Φ(u)中的本质集P是极小本质集,若P在Φ(u)中的任何本质集的族中按集合包含关系所定的序关系均是极小元。
接下来,我们讨论SSVEPD解集的本质连通区的存在性。
定理2.1对每个u=F∈M,Φ(u)中都至少存在一个极小本质集。
证明:由引理2.1知,Φ:M→2K是一个usco映射,即集值映射Φ是上半连续的,则Φ(u)本身为本质集。设Ψ是Φ(u)中所有本质集的集合,则Ψ为非空的。对Ψ任意一个非空全序子集φ,因为 φ的每个成员均为紧的,所以 φ中的所有成员之交是紧集,因而φ是有下界。根据引理1.2知,φ存在极小元,该极小元就为Φ(u)的极小本质集。证毕。
定理2.2对任何的u=F∈M,Φ(u)的每个极小本质集均为连通的。
证明:设m(u)是Φ(u)的一个极小本质集,则m(u)为Φ(u)的闭子集。如果m(u)不是连通的,则有Φ(u)中的两个非空闭子集w1(u),w2(u)以及X中的两个开子集I1,I2,使得

因为m(u)是Φ(u)的极小本质集,所以w1(u)和w2(u)均不是本质的。因此,存在两个开集S1,S2,并且w1(u)⊂S1以及w2(u)⊂S2,使得对任意的δ>0,存在u1,u2∈M以及ρ(u,u1)<δ,ρ(u,u2)<δ,但
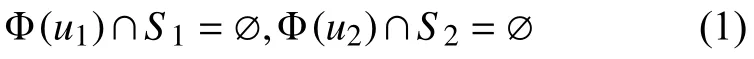
令R1=I1∩S1,R2=I2∩S2,则R1和R2均为开集,且w1(u)⊂R1,w2(u)⊂R2.因为w1(u)和w2(u)均为紧集,所以存在开集L1和L2,使得
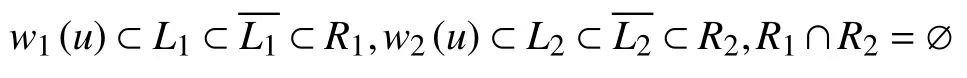
因为m(u)⊂L1∪L2,m(u)是本质的,所以存在δ′>0,使得对任何满足ρ(u,u′)<δ′的u′,有

由于L1⊂S1,L2⊂S2,则对上述的>0,由(1)式知,存在u1,u2∈M,使得
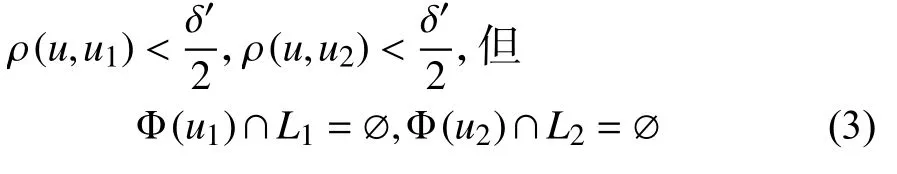
因为u1,u2∈M,则u1=F1,u2=F2。
现定义F′:K×K→2Y如下:

显然,λ(x)和µ(x)均为K上的连续函数,对∀x∈K,有λ(x)≥0,µ(x)≥0以及λ(x)+µ(x)=1.注意到F1(x,y)和F2(x,y)均为连续的,则由由引理1.1知
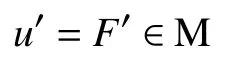
由引理2.2知
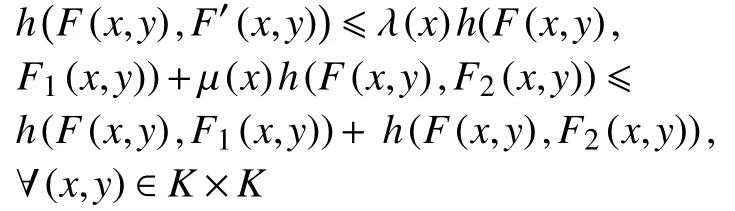
由(3)式,得
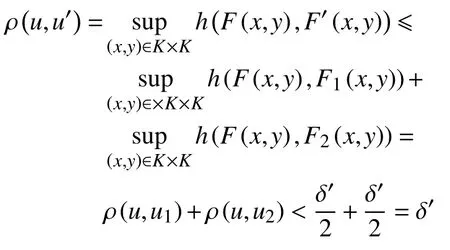
由式(2),得
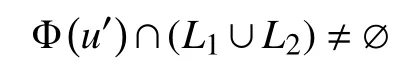
如果x∈L1,则λ(x)=1,µ(x)=0,F′(x,y)=F1(x,y).
如果x∈Φ(u′),则F′(x,y)⊂C(x),∀y∈K.于是,F1(x,y)⊂C(x),∀y∈K,则x∈Φ(u1),这与式(3)是矛盾的,故Φ(u′)∩L1=∅.
同理可证 Φ(u′)∩L2=∅,则
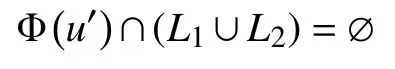
因此,m(u)为连通的。证毕。
定理2.3对∀u=F∈M,Φ(u)至少存在一个本质连通区。
证明:对∀u=F∈M,由定理2.1和定理2.2知,Φ(u)中至少存在一个连通的极小本质集P. 又因为P必包含于Φ(u)的某个连通区Φα(u),且P为本质的,所 以由定义2.2知,Φα(u)是Φ(u)的本质连通区。证毕。
3 结 论
本文在Banach空间中,当映射满足一定的条件以及序锥是扰动的情况下,证明了集值强向量均衡问题所构成的空间M中,SSVEPD解集的本质连通区的存在性定理,并将现有的集值强向量均衡问题的本质连通区,推广到具有控制结构的集值强向量均衡问题的本质连通区。
