基于改进型Stackelberg博弈的异构蜂窝网络干扰协调算法

孙 晨，吴诗弈，张 波，莫国美

（南昌航空大学 软件学院，南昌 330063）

引 言

在下一代3GPP蜂窝网络5G中，通常需要引入小蜂窝，例如设备间直通通信（Device-to-Device，D2D）和中继，来放大系统容量和/或扩大覆盖范围。这些技术已经被写入了最新版本的3GPP的移动通信系统标准[1]。D2D技术通过允许两个终端无需基站（Base Station，BS）转发而直接传输数据，来提高频率利用率并降低用户设备（User Equipment，UE）的功耗。在D2D通信带内复用的模式中，D2D链路需要与宏蜂窝网络的UE（Cellular UE，CUE）非正交地共享频率资源，这将增加可用资源以及增大CUE和D2D用户之间的干扰（DUE）。中继技术运行离基站较远的中继用户（Relay UE，RUE）通过复用CUE的频率资源来接入中继节点（Relay Node，RN），由中继节点将信息转发给基站，同样增加了可以资源和干扰。

针对中继异构蜂窝网络和D2D异构蜂窝网络的干扰协调已经被广泛的研究了，主要可以分为启发式算法，基于凸优化的算法，智能优化算法，强化学习算法和基于博弈论的算法。

Liang等人提出了一种中继异构蜂窝网络中的资源复用方法，可以有效降低中继用户对宏蜂窝用户造成的干扰[2]。文献[3]研究了D2D与宏蜂窝异构网络中的功率控制问题，通过将传统蜂窝通信的功率控制研究方案用于D2D通信功率控制。其中，功率控制方案包括固定的目标SNR功率分配、固定的发射功率分配、开环功率控制以及闭环功率控制技术，通过分析对比来评价这几种方案的性能优劣。文献[4]通过部分频率复用，将蜂窝小区划分为中心区域和边缘区域，根据D2D用户的位置为其分配资源，有效地减小了D2D与蜂窝用户之间的干扰。这些启发式算法复杂度较低，能够保证性能的改进，但难以继续提升逼近最优化。

因此，部分研究者探索了通过凸优化问题建模来解决干扰协调问题。文献[5]提出了一种中继异构蜂窝网络中动态改变资源复用数量的方法，将寻找最大化效用函数时的中继用户资源数量问题建模成了凸优化问题，并使用KKT条件进行求解，得出的动态资源复用算法比启发式的部分频率复用取得了更好的性能。文献[6]探讨了D2D异构蜂窝网络场景下的基于部分频率复用的功率控制问题，在部分功率控制的基础上提出了动态功率控制。以小区系统吞吐量最大化为目标，建立功率控制的目标函数，将非凸函数转化为凸函数，并对拉格朗日对偶分解方法进行了改进，降低了算法的复杂度。基于凸优化的干扰协调算法通过建立优化目标和求解凸优化得出近似最优解，但理想化的优化目标建模和求解过程中的NP难问题也会使得这些算法需要退而求其次。

部分研究者也尝试了使用智能优化算法来解决目标优化中的NP难问题。文献[7]提出了一种基于遗传算法的联合资源分配与用户匹配方案来最小化干扰并最大化频谱效率，实现了使用有限数量的资源块为大量用户提供服务的优点。并且，该方法具有优越的性能和快速收敛的性能。文献[8]提出了两种基于PSO（粒子群优化）和混合PSO-GA（遗传算法）的资源分配方案，通过允许最多两个D2D对与一个CUE共享同一频率资源来最大化系统吞吐量。其中，提出的混合PSO-GA可以改善粒子的多样性，从而避免局部最优。

智能优化算法依然将优化目标建模成理想化的数学模型，而强化学习算法可以通过真实网络的结果反馈来实现目标优化。文献[9]提出利用Qlearning来让小蜂窝基站学习合适的发射功率，以减少小蜂窝基站间的干扰。文献[10]中提出一种多智能体的Q-learning方法用于D2D多层异构网络的中D2D用户进行频率资源选择。这两种方法需要解决的问题是迭代次数过多和陷入局部最优解。

很多研究也从博弈论的角度来解决干扰协调问题。文献[11]考虑了多小区中继网络中的非合作分配博弈，它仅旨在通过资源分配来提高系统吞吐量，而忽略了功率能效的问题。文献[12]在宏蜂窝通信和中继通信系统下，提出了基于博弈论的功率控制和资源分配算法。与等功率分配相比，使用较低的传输功率，可以达到系统的吞吐量提高的目的。文献[13]提出了一种改进的基于博弈论的D2D通信功率算法，作者在提高系统吞吐量的同时，在算法中还将代价因素引入效用函数，用户具有更高的公平性。文献[14]把下行系统总传输速率最大化的资源分配问题建模成拍卖模型，使用了反向迭代组合拍卖机制，所有D2D链路的集合作为组合拍卖物，资源作为竞拍者。文献[15]中的资源分配使用了Stackelberg博弈模型，该模型中根据决策行动次序将博弈方区分为领导者和跟随者，领导者首先决定某个参数，而跟随者根据这个参数做出决策，通常用于地位不对等的博弈双方，与D2D链路和宏蜂窝链路之间的关系较为类似。文献[15]的作者将已经分配了资源的宏蜂窝链路视为领导者，D2D链路视为跟随者，以优化宏蜂窝链路和D2D链路的传输速率为目标进行了链路的配对。

在Stackelberg博弈模型中，双方的成本参数是重要的参量，将会影响两阶段博弈的结果。因此，有一些研究提出了不同的成本参数设置方法。文献[16]提出人为调整成本参数来保证反应方程等号两边是相同的数量级，反应方程的值在合理的范围内。也有研究提出成本参数由跟随者的信道状态来决定[17]，或者由领导者的信道状态决定[18]。文献[19]提出了一种迭代更新的成本参数改进策略，根据博弈结果按固定步长更新全局成本参数。文献[20]则证明了需要为每个信道的每个D2D链路设置一个成本参数。在目前的基于Stackelberg博弈的干扰协调算法研究中，成本参数大多是固定的或是自迭代更新的，尚缺乏优化机制的探索，难以保证Stackelberg博弈的有效性。

本文关注在D2D和中继异构蜂窝网络中使用Stackelberg博弈模型解决干扰协调问题，做出了以下贡献：

1）使用Stackelberg博弈模型对于D2D和中继异构蜂窝网络中的干扰协调问题进行了建模，提出了D2D和中继用户上行发射功率控制算法，提出D2D和中继用户与宏蜂窝用户之间的配对算法，实现了对D2D和中继用户的资源分配和功率控制，减少了链路之间的干扰问题；

2）提出了一种成本参数训练和更新的强化学习算法，通过现有成本参数和宏蜂窝用户信道条件为状态空间，成本参数更新动作为动作空间，用户传输速率为回报的强化学习训练框架，寻找出较优的成本参数状态，并通过epsilon-greedy算法执行成本参数的更新；

3）通过仿真实验验证了成本参数改进后，基于Stackelberg博弈的干扰协调算法相较其他算法的性能提高，以及成本参数改进的效果。

1 系统模型

本文考虑研究的系统是由一个基站BS和一个中继节点RN的单蜂窝小区，其中包含若干宏蜂窝用户设备CUEs和D2D通信用户设备DUE。在蜂窝上行通信链路中，M个宏蜂窝用户设备（CUEs）和Q个中继用户设备（RUEs）分别与基站BS和中继节点RN进行通信。N对D2D用户，其发射端（DTx）和D2D接收端（DRx）之间的链路，可以复用蜂窝用户CUE的上行链路资源进行数据通信。带内RUE-RN链路与接入子帧中的某些CUE-BS链路使用相同的物理资源块（PRBs），并且为了避免在RN处的自干扰，RN-BS链路和RN-BS链路在回程子帧中与CUE-BS链路正交地共享PRB。因此，CUE-BS链路可能会受到来自RUE和DTx的干扰，同时CUE还可能是DRx上D2D链路和RN上RUE-RN链路的干扰源。

因此，蜂窝用户CUE的上行链路中某个CUE在某个PRB上接收到的信噪比SINR为：

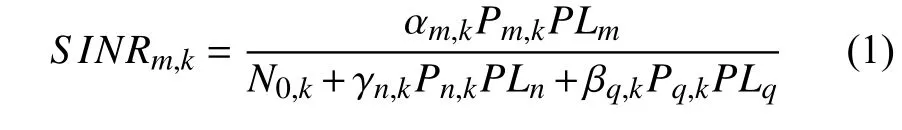
其中，Pm,k表示第m个蜂窝用户CUE在使用第k个PRB时的发射功率；Pn,k表示第n对D2D用户的发射端DTx在使用第k个PRB时的发射功率；Pq,k表示第q个中继用户RUE在使用第k个PRB时的发射功率。同样地，PLm表示第m个蜂窝用户CUE与基站BS之间的链路（即CUE-BS）的路径损耗，PLn表示第n对D2D用户的发射端DTx与基站BS之间的链路（即DTx-BS）的路径损耗，PLn表示第q个中继用户RUE与基站BS之间的链路（即RUE-BS）的路径损耗。此外，N0,k表示高斯白噪声，二进制变量αm,k、βq,k和γn,k表示复用系数，0表示不复用资源，1表示复用资源。

D2D进行上行通信时，其某对D2D的接收端DRx在某个PRB上接收到的信噪比SINR可以表示为：

其中，PLm,n表示第m个蜂窝用户与第n对D2D用户之间的链路的路径损耗，PLq,n表示第q个中继用户与第n对D2D用户的接收端DRx之间的链路的路径损耗。

同样地，中继用户RUE在回传链路进行上行通信时，某个RUE在某个PRB上接收到的信噪比SINR为：

其中，PLm,q表示第m个蜂窝用户与第q个中继用户之间的链路的路径损耗，PLn,q表示第n对D2D用户的发射端DTx与第q个中继用户之间的链路的路径损耗。

综上，整个蜂窝通信系统在带宽为B的PRBk上的总数据传输速率可以表示为：

在本文中干扰协调的目的是使每个PRB上所有链路可以达到最大化的系统吞吐量，其目标函数可以表示为：受限于：

其中，Pq,min和Pq,max分别表示中继通信用户设备RUEq所允许的最小发射功率和最大发射功率；Pn,min和Pn,max分别表示D2D用户对n的发射端所允许的最小发射功率和最大发射功率。

2 基于Stackelberg博弈的干扰协调算法

为了实现分布式干扰协调决策，本研究通过使用Stackelberg两步博弈模型来让D2D用户对/RUE发射功率控制和其资源分配分别在小蜂窝（D2D/RUE）和宏蜂窝基站BS进行决策。小蜂窝（D2D/RUE）上进行的博弈是跟随者博弈，宏蜂窝基站处进行的博弈是领导者博弈。异构蜂窝网络中，宏蜂窝处于核心地位，小蜂窝被认为是补充和辅助，系统性能以保证小蜂窝基本性能的前提下，使宏蜂窝性能尽可能少地受到干扰的影响。因此，使用Stackelberg两步博弈模型来对干扰协调建模是符合实际应用需求的。

2.1 领导者效用函数

在领导者博弈中，效用函数可由在PRBk中，CUEm、D2D用户对n以及RUEq组成，其可以表示为：

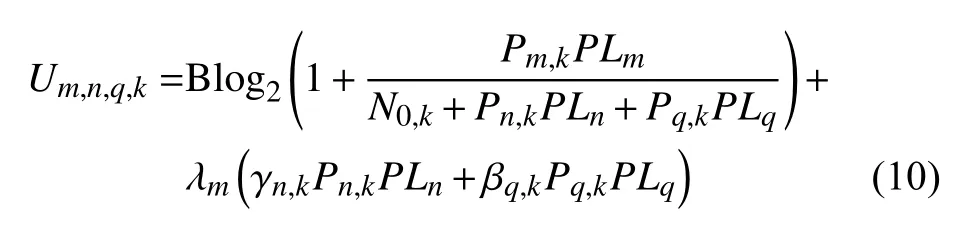
其中，λm是每个CUEm提供给任何其他复用链路的成本参数。此外，复用系数γn,k和βq,k∈{0,1}，且它们无法同时为1，即D2D对和RUE不能复用同一个CUE的链路资源。

2.2 跟随者效用函数

在跟随者博弈中，D2D对n和RUEq在PRBk中的支付效用函数可以分别表示为：

在本研究所提出的模型中，既不考虑D2D与RUE之间的资源复用，也不考虑不同D2D对之间的资源复用。

2.3 小蜂窝决策的功率控制算法

在小蜂窝（D2D和RUE）处，发射功率由追随者效用函数求偏导计算得出。以求解D2D的发射功率为例，用式（11）求对Pn,k的偏导函数，并令其为0，可以得到针对不同λm的D2D最佳发射功率。

同样地，也可以通过式（12）求对Pq,k的偏导函数，并令其为0，可以得到RUE的最佳发射功率：

2.4 宏蜂窝决策的资源分配算法

为了实现式（18）中的优化目标，本研究采用了匈牙利算法来实现。具体实现步骤如下：

第一步：遍历Um,n,q,k矩阵中所有的列，在这N+Q个列中分别寻找Um,n,q,k最大值，及其对应的所有行m；

第二步：判断所有的m是否为不一样的数。如果是跳至第四步；

第三步：找出所有不重复的行m，及其对应的列n或q，将其剔除出Um,n,q,k矩阵，（注：由于N +Q应小于M，因此矩阵必不为空），重复第一步；

第四步：输出所有(m,n)和(m,q)的对应关系，以Round-Robin算法将所有的资源k公平地分配为(m,n)和(m,q)，以及未复用的CUE。

3 基于强化学习的成本参数改进算法

由于在上文所提出的博弈模型中，成本参数λm是关键因素，它决定了D2D对的发射端DTx和中继用户RUE的发射功率，也影响了D2D/RUE和CUE之间的资源复用。但是，为CUEm设置一个好的λm是困难的，它应该让D2D/RUE的发射功率位于适当的范围内，以实现功率控制。因此，本章提出了一种基于蒙特卡洛的离线强化学习算法，通过动态调整成本参数，实现通信系统性能的进一步优化。

3.1 强化学习模型

强化学习常用于智能体在与环境交互过程中通过学习在特定状态下执行何种动作以达到累计回报最大的目标。不同于监督学习和非监督学习，强化学习不需要预先给定数据集，而是需要定义智能体和状态-动作-奖励三元组变量。

每个CUEm在每个时隙t中执行学习过程以更新三元组变量，该变量是状态s，动作a和奖励r。成本参数的强化学习模型的各个组成变量定义如下：

状态：定义为K个PRB上的CUE-BS链路的路径损耗s；

动作：定义一组价格因素λm为动作a，在本研究中取值空间设定为a(t)∈(2×1013,5×1019)；

奖励r(t)即回报函数：回报函数反应了学习的目标，定义为表示D2D / RUE复用CUE的链路资源与D2D / RUE没有复用CUE的链路资源时，它们之间取对数吞吐量的差值，即：

3.2 更新和训练算法

上文已经定义了状态，动作和奖励（即回报函数）。状态和动作将组成Q表，根据训练算法在奖励的作用下进行更新。具体实现过程由两个步骤组成：

第一个过程是Q值进行更新的过程。由宏蜂窝基站构建Q表，表中的每一个Q值Q(s,a)反映的是状态s下采取动作a的累计奖励。Q(s,a)的更新算法如下：

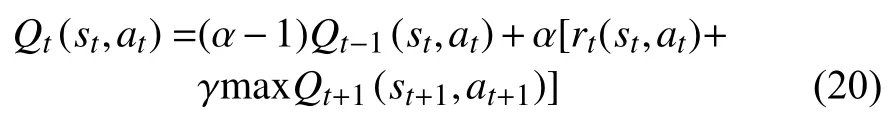
其中，α为学习率，表征Q值的更新速度，在本研究中设定为0.01。γ为折扣率，表示最终奖励对中间状态的影响，在本研究中需要设定为0。

第二个过程是根据Q表选择动作，并执行动作，从而产生奖励的训练过程。和第一个过程首尾相连，形成“动作执行-产生奖励-更新Q表-更新动作选择”的循环。根据Q表进行动作选择的算法有很多，本研究选择了ε−greedy算法。在ε−greedy算法中，一般称到目前为止发现是最好的或者其对应Q值最高的动作作为贪婪动作。其中，在动作选择的贪婪策略中，以 ε的概率选择其他动作，以(1−ε)的概率选择贪婪动作。ε的值决定了探索和决策之间的平衡。在本研究中，在学习的初始阶段选择 ε的值接近1，这样做的目的是避免发生死循环，同时还可以让其有机会跳出局部最优。ε的值会随着学习的不断进行逐步减小，当它达到学习的最后阶段，贪婪动作就会成为最佳动作，从而达到Q−table收敛的程度。

4 仿真实验

本研究进行了单扇区的系统级仿真，拟比较所提出的算法和基准方法的系统性能优劣。在仿真实验中，在一个扇区内随机分布了不同通信方式的用户设备，其中包含30个CUE/RUE和若干D2D对用户设备。具体参数设置如下表1所示。

表1 系统仿真参数

本文考虑了两种基准算法作为比较算法。第1种，在基于Round-Robin的资源分配算法中，RUE和D2D对随机复用CUE的链路资源，而不考虑它们的信道信息和功率的优先级，这里称为“RR”算法；第2种，在不进行功率控制的贪婪优化算法中，每个PRB上的CUE和RUE/D2D对的吞吐量之和进行优化，而不考虑减少它们之间的干扰，标记为“GO”算法。此外，在GO方案中，D2D用户的发射端DTx和RUE的最大发射功率被设置为不同的发射节点。

本章提出的基于改进型Stackelberg博弈的干扰协调算法，将与上述两个基准算法进行一些性能指标的比较，例如：平均吞吐量，5%最低吞吐量以及通用比例公平（Generalized Proportional Fairness，GPF）等。

其中，GPF的定义如下：

如图1所示，反映了使用不同资源分配和功率控制算法的CUE吞吐量的累积分布函数（CDF）。与RR算法和GO算法相比，本研究所提算法对吞吐量低于800 Kbps左右的CUE具有更大的性能。这意味着，所提出的算法可以缓解部分CUE受到使用相同资源的D2D对的干扰，从而改善其信道状况。

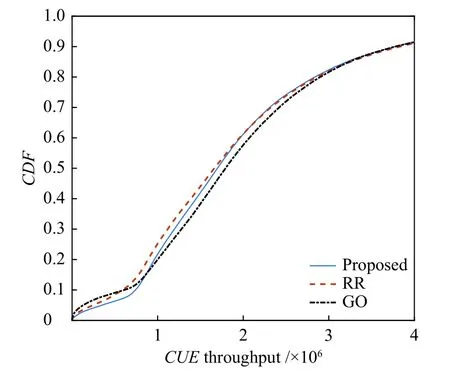
图1 CUE的吞吐量CDF

随着D2D对数量的增加，图2给出了CUE的平均GPF。从图中可以反映，随着D2D对数的增加，导致其对CUE的干扰不断增加，因而增加D2D对将降低CUE的平均GPF。从图中可以看出，就两个对比算法而言，使用GO算法的CUE的平均GPF在D2D对数较少的情况下具有较大的值，而在D2D对数较多的情况下，RR算法则优于GO算法；但是，从图中可以明显看出，本研究所提出的算法的CUE的平均GPF一直优于其他两种算法。

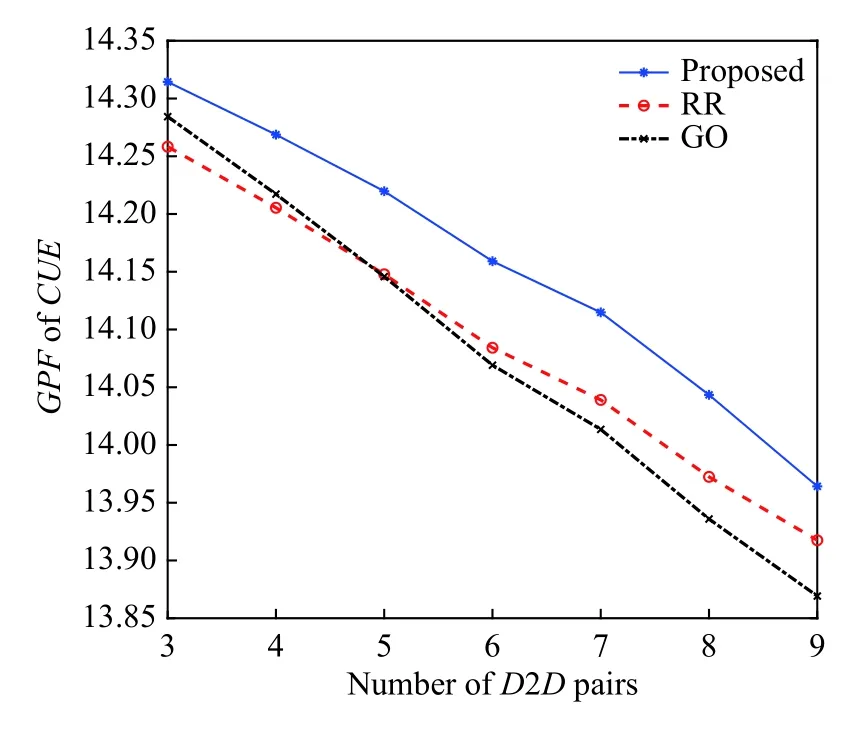
图2 不同D2D对数下的CUE的GPF

如图3所示，反映了各个算法在不同D2D对数下的5%最低吞吐量的变化情况。从图中可以看出，当D2D对的数目从3个增加到6个时，CUE的5%最低吞吐量在使用GO算法的情况下，从500 Kbps显著下降到80 Kbps；使用RR算法时，其吞吐量从460 Kbps下降到180 Kbps；而使用本研究所提的算法，虽然吞吐量从640 Kbps下降到了240 Kbps，但是相比于GO算法也有一定的优越性。

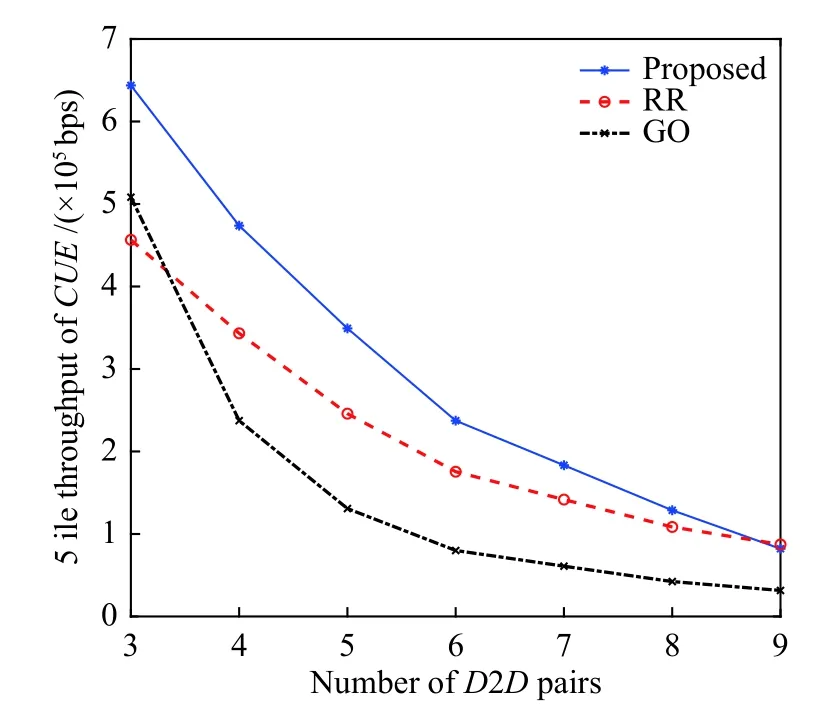
图3 不同D2D对数下的CUE的5%最低吞吐量

从图4中可以看出，当中继节点RN远离基站BS时，使用不同算法的CUE的GPF都会随之增加，这是因为边缘信号质量不好的用户随着中继节点的靠近，使得其信号质量得到了较大的改善。与此同时，如图5所示，基站和中继节点之间距离变化下的CUE的5%最低吞吐量在各个算法下的情况相差较大。从图中可以清楚的看出，与RR和GO算法相比，本研究所提出的算法下CUE的GPF和5%最低吞吐量具有显著优势。

图4 基站和中继节点之间距离变化下的CUE的GPF

图5 基站和中继节点之间距离变化下的CUE的5%最低吞吐量

5 结 论

本研究改进了基于Stackelberg博弈的干扰协调算法使其应用于D2D和中继多种小蜂窝与宏蜂窝共存的异构蜂窝网络。在这个基础上，提出了一种Stackelberg博弈中成本参数的改进方法，利用了强化学习算法，获得了较好的博弈效果。从仿真实验的结果可以看出，基于Stackelberg博弈的干扰协同算法相比对比算法，可以有效地降低对CUE的干扰，提高异构蜂窝网络性能，而成本参数的训练和更新方法可以进一步扩大这种优点。因此，本研究所提出的算法在提高异构蜂窝网络性能方面具有明显的有效性。下一步的研究中将考虑不同的学习率和不同的ε-greedy算法对于收敛性的影响。