分层加密网格的悬链面膜结构数值找形优化

2021-11-21张少钦李云鹏

南昌航空大学学报（自然科学版） 2021年3期

于琪，张少钦，熊磊，李云鹏

（南昌航空大学土木建筑学院，南昌 330063）

引言

膜结构作为一种柔性结构，其膜材不能抗压、抗弯，故需要在符合给定边界条件的情况下，通过施加一定的初始预应力使膜面产生只有张力作用的自平衡曲面来维持结构形状和抵抗外荷载，这种由应力分布状态求解结构形状的过程常被称为找形（form finding）。从膜结构分析的三个过程（初始形态分析、荷载效应分析和裁剪分析）来看，初始形态分析（找形）是膜结构分析过程中最为活跃、最为关键的部分，结构初始形态的好坏直接影响后续分析过程[1]。

从最开始的物理找形到近年来的数值找形，众多学者广泛探索有效的找形方法及不断加以改进。用于膜结构初始形态确定的数值方法主要有：力密度法(Force Density Method)[2]、动力松弛法(Dynamic Relaxation Method)[3]和非线性有限元法(Nonlinear Finite Element Method)[4]。在计算机软硬件飞速发展的今天，非线性有限元法应用更为广泛[5]。利用非线性有限元法确定膜结构初始形态的计算方法主要包括节点平衡法和支座移动法[6]。卫东等[6]在对具体薄膜结构算例进行初始形态确定的过程中，通过对各种传统方法的分析比较，提出了综合节点平衡法。叶继红等[7]根据建筑师对膜面造型的变化要求，针对动力松弛法中阻尼参数的取值，对常规动力松弛法进行了改进。周树路等[8]针对力密度法进行膜结构找形时总需要多次试算才能确定合适的力密度取值的相关问题，提出了改进找形过程的措施。魏德敏等[5]通过计算发现，膜的预张力、单元的划分、边索和脊索的预张拉力值以及初始弹性模量等参数的选取都会影响找形结果。纵智育等[9]根据几何非线性有限元理论，提出运用新的8结点曲面四边形等参单元进行张力膜结构找形分析的具体做法。袁驷等[10]提出一种基于EEP（单元能量投影）法的二维非线性有限元自适应方法，成功将之应用于膜结构的找形分析。

针对结构找形分析过程中，采用传统网格加密方法能提高结构找形精度但计算量较大且效率低下的问题，本文从调整有限元网格的角度，提出了一种在保证单元总量不变的情况下，通过分层加密网格的方式来实现膜结构找形优化的方法，并结合具体的悬链面膜结构算例验证其有效性。

1 悬链面膜结构数值找形优化的实现

1.1 数值找形的实现

悬链面（图1）是旋转面中唯一有解析解的最小曲面，其曲面方程为：

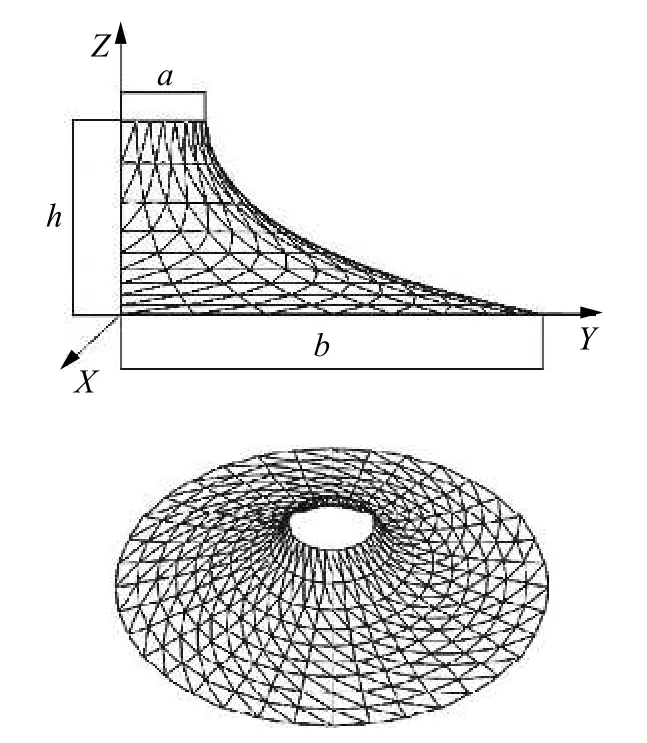
图1 悬链面结构模型示意图[6]

其中，a表示悬链面内圆半径，h表示悬链面高度，，其含义为结构内任一高度上圆的半径，(X，Y，Z)为悬链面内节点坐标。h的求解方法如下式所示。

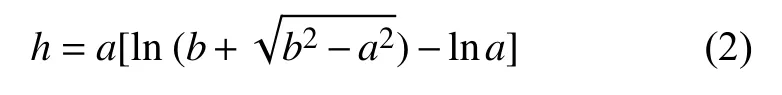
其中，b表示悬链面外圆半径。

基于ANSYS软件采用节点平衡法对悬链面膜结构进行数值找形，具体流程如下：

采用SHELL41三维壳体单元模拟悬链面膜面，建立初始形状（可通过曲面拟合[6]等方式得到）模型，设定很小的弹性模量（如取实际弹性模量的10−3~10−6），利用式(3)[11]将膜面初始预应力转换为下降温度值施加于膜单元以确定其平衡曲面（称为第一次找形）；进行模型修正，直到膜面应力趋于相等或满足一定的应力误差为止，得到近似的最小曲面（称为第二次找形）[12]。

其中，ΔT为温度下降值；σ为膜面初始预应力；E为膜材弹性模量；α为膨胀系数；t为膜材厚度。

1.2 分层加密网格的实现

分层加密网格分两步进行。第一步，根据初始条件进行结构有限元建模及分析，求出正常网格划分情况下的膜面数值解与解析解误差。第二步，重新建立模型，对原结构误差数值相近的区域进行归类，将结构划分为不同的网格划分区域，在单元总量保持不变的情况下，对误差较小区域采用较稀疏的网格，对误差较大区域则将网格划分的密集。这就达到了分析计算量增加不大的同时使结构找形结果得到优化的目的。

首先，全面收集区域概况资料、土壤污染源资料、土壤环境和农产品资料及其对应的图件资料等，并通过分析，研究有关信息划分区域内的地理单元，为污染风险评价提供基础支撑；其次，通过评估土壤及农产品调查点位的土壤重金属污染情况、农产品重金属污染情况，反映该点位土壤和农产品重金属污染状况，划分点位土壤重金属风险等级，为区域风险评价提供基础依据；最后，通过评价单元内土壤重金属污染风险、农产品重金属危害风险、重金属生物可利用性等因素的情况，反映区域内耕地土壤和农产品重金属污染情况，划分区域内土壤重金属风险等级，为重金属污染耕地分级管理提供依据。

以悬链面1/4结构平面图模型为例，分层加密网格法的实现过程如下：

首先建立正常网格划分方法下的结构模型，将模型周向圆弧边及径向直线边划分为12等份，得到如图2所示网格尺寸为12×12的结构模型。

图2 悬链面1/4结构(平面展开)网格

按照图2所示网格划分方式求得结构数值解与解析解误差后，依据误差数值相近进行归类的原则，对重新建立的结构模型进行结构网格区域划分，如图3a所示。其中，A、B、C、D表示不同节点数值解与解析解误差对应区域。根据分析结果，在误差的数量关系上从区域A至区域D误差逐级递增，实际结构划分区域数视误差情况而定。将图3a中四个区域从A至D逐级加密网格。具体做法为：周向圆弧边上各区域网格划分份数相同，径向直线边上每个区域按等分方式划分网格，由于每个区域径向宽度不同（越靠近小圆，径向宽度越小），此法就实现了从外圆至内圆分层加密网格的构想，网格划分结果如图3b所示。

图3 分层加密网格法示意图

2 计算结果与分析

算例取内圆半径a=8 m，外圆半径b=40 m，高度h=18.339 5 m。结构上下边界均固定，初始预应力σ=2.5 MPa，弹性模量E=250 MPa，厚度t=1 mm，泊松比μ=0.34，膨胀系数α=0.01。采用两种不同的网格尺寸（1/4结构网格尺寸分别为策略一：12 ×12和策略二：16×16），对正常网格划分以及采用分层加密网格法下（网格调整前后）结构变形图、应力云图及节点数值解与解析解误差进行对比分析。

2.1 策略一结果对比

图4中，网格调整前后结构单元及节点总量保持不变，其中单元有1152个，节点624个。基于图4可以看出，采用分层加密网格法下的结构网格分布更加均匀，特别是靠近小圆位置，结构曲面较前者更为平滑。

图4 策略一结构变形云图

从图5可以得出，网格调整前结构应力在4.27~4.68 MPa之间，应力差值为0.41 MPa，网格调整后的结构应力分布在4.38~4.72 MPa之间，应力差值为0.34 MPa。整体应力方面，网格调整后增加了约2.5%，应力稍有提高；应力差值方面，网格调整后降低了约20.5%，结构应力分布较网格调整前提高明显。

图5 策略一结构应力云图(俯视图)

由于悬链面是旋转面[13]，其在各个方向上变化相同，为了方便计算，在判断节点数值解与解析解误差时，文章选取的节点均在XZ轴平面内，故Y坐标取为0。此外，结构边界上的节点未产生位移，即不存在误差，故未在表中列出。

表1 策略一网格调整前节点数值解与解析解误差

表2 策略一网格调整后节点数值解与解析解误差

表3 策略一坐标相近节点误差对比

2.2 策略二结果对比

图6中，网格调整前后结构单元及节点个数相同，其中单元个数为2048个，节点1088个。由图6可以看出，新方法下的结构网格分布较前者更加均匀，曲面也更为平滑。

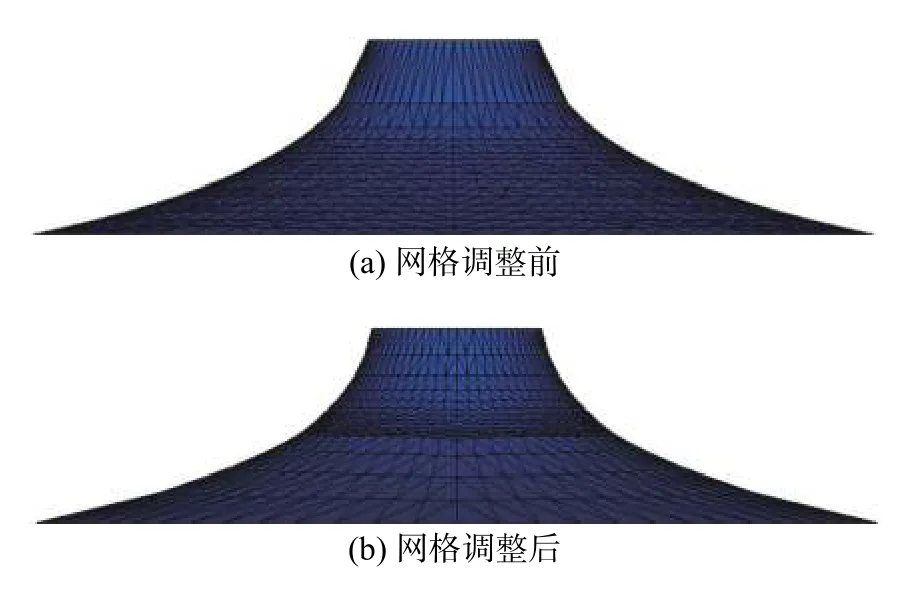
图6 策略二结构变形云图

依据图7，网格调整前结构应力在4.28~4.65 MPa之间，应力差值为0.37 MPa，网格调整后的结构应力分布在4.38~4.72 MPa之间，应力差值为0.34 MPa。整体应力方面，网格调整后增加了约2.3%，应力稍有提高；应力差值方面，网格调整后减小了约9%，结构应力分布较网格调整前也有一定减小。