一种求解多介质流问题的正保护数值方法

陈凌蕙，徐 伟

（南昌航空大学 数学与信息科学学院，南昌 330063）

引 言

在对多介质流进行数值模拟时，有时会遇到流体的密度、压力或内能非常小的情况，如爆炸、高速射流及惯性约束核聚变等问题。此时用传统的高精度格式，如WENO，DG等进行求解，常会由于数值误差而得到负的密度或压力值，而这显然是不符合实际情况的，同时这也会使得算法不稳定，从而导致计算失败。针对这类问题，目前已有一些研究工作，发展出了一些具有正保护功能的数值算法，但大多是针对单介质流体的，而对于多介质流的相关工作则相对较少。这是因为，多介质流体在介质界面两边的密度与压力等状态常常会相差巨大，其所使用的状态方程也不尽相同，甚至不同介质使用的控制方程有时也不一样，这些都使得构造求解多介质流动问题的正保护数值算法要困难得多。解决这类问题的一个简单的方法是强行将负的密度或压力值等赋值为零，但这会使得算法的精度和守恒性都无法得到保证。Einfeldt在早期给出了一类求解可压缩Euler方程的，具有正保护功能的Godunov格式[1]，但是只有一阶精度。Perthame则分别给出了具有正保护功能的一阶Lax-Friedrichs格式[2]和二阶Boltzmann格式[3]。然而要想将这些格式中给出的正保护方法在不破坏精度的条件下，推广运用于任意高精度格式是非常困难的。Zhang和Shu在上述Lax-Friedrichs格式的基础上给出了一种更易于推广到高精度的正保护格式构造方法[4]，并给出了判断格式是否具有正保护性质的充分条件，但这种方法只是适用于理想气体。Cheng和Shu则结合HLLC方法和Lagrange方法，给出了一种针对多介质流动问题，且具有正保护功能的数值算法[5]。上述方法进行正保护的大致思路都是通过构造正保护限制器，进而利用限制器对计算出现的负密度负压力等值进行修正，同时保证不破坏格式原有的精度及守恒性。

另外，在求解多介质流问题时，若直接使用传统的高精度格式，由于介质界面两边流体状态方程的不同，数值结果在界面附近会出现非物理振荡或计算失败。针对该问题，Fedkiw等给出了一种GFM方法[6]，这种方法通过在界面附近定义虚拟流体，将多介质问题转化为多个单介质问题，然后再使用已有的高精度方法进行计算。最初的GFM方法在计算时，将虚拟流体的压力与速度值取为当地数值，再由熵修正得到密度。但是在计算水-气多介质流时，该算法的稳定性较差，从而产生了一些变形，如nGFM法[7]、mGFM法[8]以及rGFM法[9]等。其中mGFM法与rGFM法都是通过在介质界面附近构造黎曼问题，并利用黎曼问题的解来对界面附近的单元进行特殊处理。不同的是，mGFM法只对虚拟流体中的单元进行定义，而在真实流体中只对密度进行等熵修正。这种做法实际上使得真实流体与虚拟流体在界面附近的单元没有得到同步更新，从而在计算某些问题时还是会出现虚假振荡。而rGFM法则利用黎曼问题的解同时对真实流体与虚拟流体进行更新，能更真实的反映流体的特性。

由上述可知，在计算多介质流问题时，有两处需要进行正保护，一是在界面处计算黎曼问题的时候，一是对各单介质进行计算的时候。本文基于正保护限制器[4]与正保护HLLC方法[5]，给出了一种适用于气-气及水-气多介质问题的正保护数值算法，并通过多个算例验证了算法的有效性。

1 方 程

1.1 控制方程

一维无粘可压缩Euler方程：

其中U=(ρ,ρu,E)T，F(U)=(ρu,ρu2+p,(E+p)u)T，E=ρe+ρu2/2，式中的ρ是密度，u是速度，p是压强，e是单位质量的内能，E是单位体积的总能。

二维无粘可压缩Euler方程：

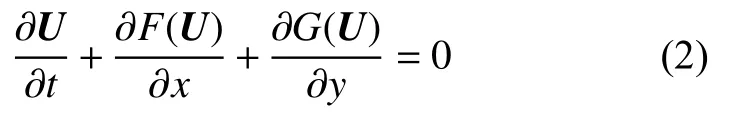
其中

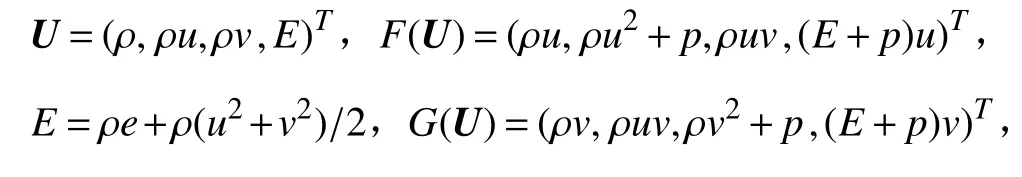
式中的ρ，e与E的含义与一维情况一样，而u是v则分别 表示x和y方向上的速度。

1.2 状态方程

为了求解Euler方程，需要给出流体的状态方程。当流体为理想气体时，其方程为：

而水的状态方程有多种，本文取

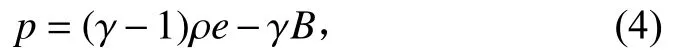
其中γ与B为热力学常数，将在具体算例中给出。不难看出气体与水的状态方程可以表示成统一的形式。此外，式（4）也可写为p+B=(γ−1)(ρe−B)。

2 正保护数值方法

2.1 正保护有限体积法

对于一维情况，首先取点集G：

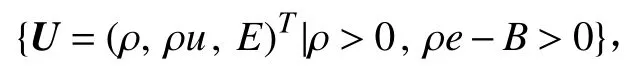
利用Jensen不等式易证G为凸集。而所谓正保护格式，即要使得当Un∈G时，能够有Un+1∈G。

考虑有限体积法的一般形式：

其中，m=ρu。接着取单元Ij上的Gauss-Lobatto点集

且有2N−3≥k。

由文献[4]可知，对于有限体积格式（5），若在tn时刻，∀α,j，有以及。则在CFL条件：

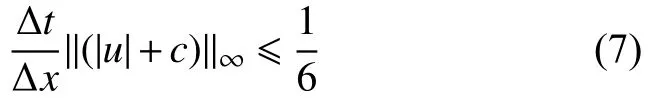
可得tn+1时刻的∈G。

根据上述结论，下面将给出正保护限制器对单元Ij上的重构多项式qj(x)进行修正，使得修正后的满足：

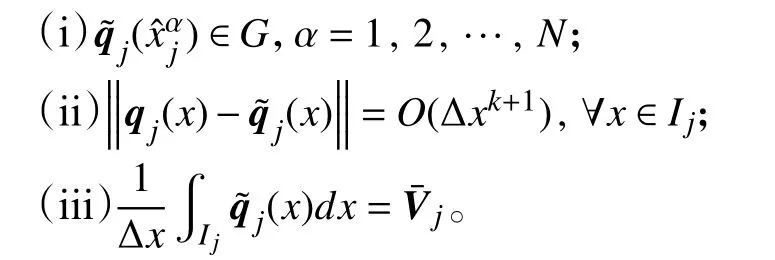
修正将分两步进行，具体如下：

首先，密度修正：在各单元Ij上，将密度函数ρj(x)修正为，即取

其中

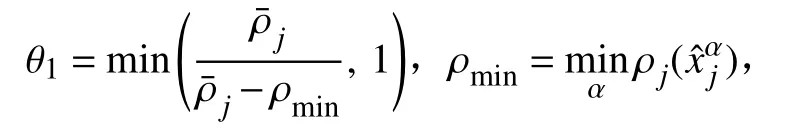
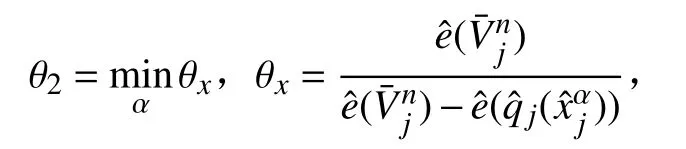
于是

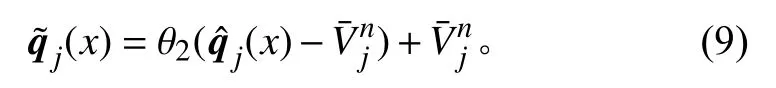
本文采用WENO方法进行空间离散，但由于WENO格式与DG格式不同，它不给出重构多项式的具体形式，而是直接得到点值与。因此为了使用上述限制器对重构多项式进行修正，可以按文献[10]中的方式得到重构多项式，再对其进行修正，继而利用修正后的多项式再计算出所需的点值与。而时间离散则使用三阶Runge-Kutta时间离散，式（5）实际上就是其中的第一步。由于其后两步都是凸组合的形式，因此格式仍然具有正保护性质。

对于二维情况，不妨设区域被划分为若干矩形网格单元Iij。在每个小矩形网格单元中，取如下点集：

与一维情况类似，若在tn时刻，∀α,β,i,j，有。则在CFL条件：

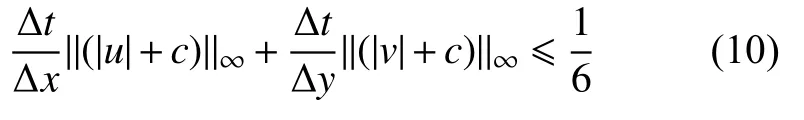
可得tn+1时刻的。其中qij(x,y)为单元Iij上 各守恒量的k次近似多项式向量(ρij(x,y),mij(x,y),ni j(x,y),Eij(x,y))T。因此，二维情形下正保护限制器的构造及修正方式也与一维情形均基本相同。

2.2 正保护界面处理方法

本文采用rGFM方法来重定义界面两侧的流体状态。使用该方法需要在界面处求解黎曼问题，因此也需要一种具有正保护功能的算法。

首先考虑一维情况。假设界面位于单元j与j+1之间，如图1所示。

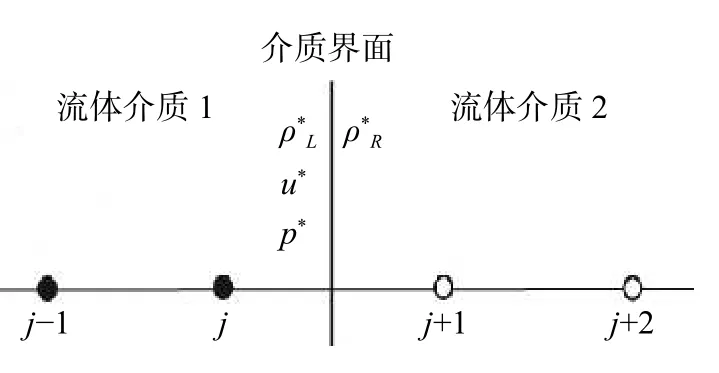
图1 一维界面边界条件定义

于是构造如下黎曼问题：

对于求解黎曼问题，已有许多成熟的求解器。本文采用基于双激波近似的HLLC求解器，如图2所示。

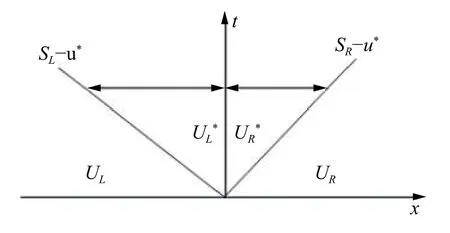
图2 双激波近似黎曼问题

图中的u∗是介质界面的速度，sL与sR分别是左右激波的波速，是该黎曼问题的解。以左激波为例，由于流体在激波两侧的状态满足Rankine-Hugoniot条件，则有

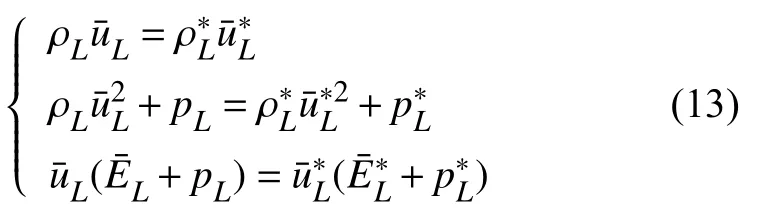
其中

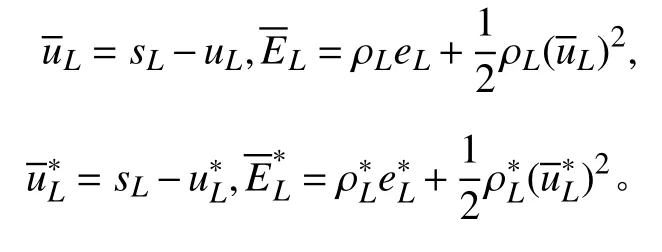
而对于右侧激波则可以得到类似的式子。又由于在介质界面处的速度和压力连续，即有。于是由上述等式可得黎曼问题的近似解：

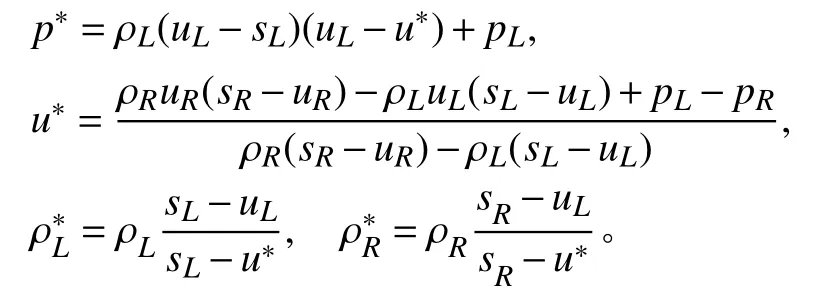
可以证明，当取

sL=min(uL−cL,−),sR=max(uR+cR,+),

而对于二维多介质问题，则需要沿介质界面的法向构造并求解黎曼问题[9]。由于此时得到的黎曼问题仍是一维形式，因此可以使用上面给出的正保护方法进行求解。与一维问题相比，二维问题中介质界面的追踪要复杂的多，本文采用Level Set方法[11-12]对界面进行追踪。

3 数值实验

下面将通过几个数值算例来验证算法的有效性。这些算例由于初始条件比较极端，因此会出现低密度低内能区域，传统高精度方法容易算得负值，从而导致程序崩溃。

算例1 气−气双稀疏波问题

该问题的计算区域为[−1,1]，介质界面位于区域中心。其左侧流体的初始状态为：

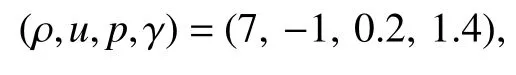
右侧的初始状态为：

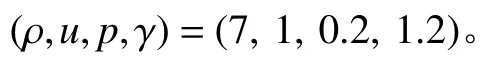
在该问题中，介质界面两侧的流体同时向两侧反向运动，从而产生两个强稀疏波，使得中心区域的压力大幅下降，几乎形成真空。图3给出了网格数为300，t=0.6时的数值结果。

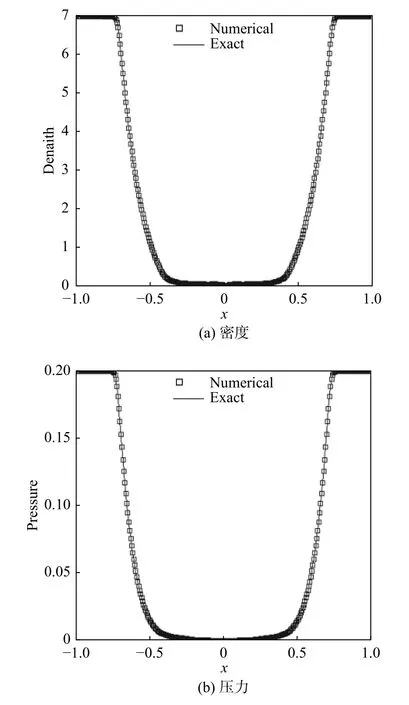
图3 t=0.6时的数值解

算例2 气−液激波管问题

这是一个气−液多介质流问题，计算区域为[0,1]，介质界面位于x=0.3处。界面左边气体的初始状态为：

右边液体的状态为：

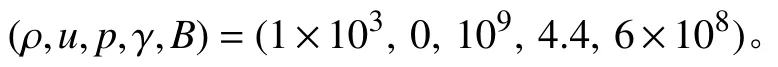
该问题是一个极端条件问题，两侧流体的初始压力p与状态方程中的参数B相差非常大。随着时间推进，将形成一个向左的激波和一个向右的稀疏波，图4给出了t=0.000 24时刻，网格数取为300的数值结果。可以看到，即使两种流体的物理特性及初始条件都相差较大，本文给出的正保护算法依然能准确的捕捉到各种间断，并且介质界面非常清晰。

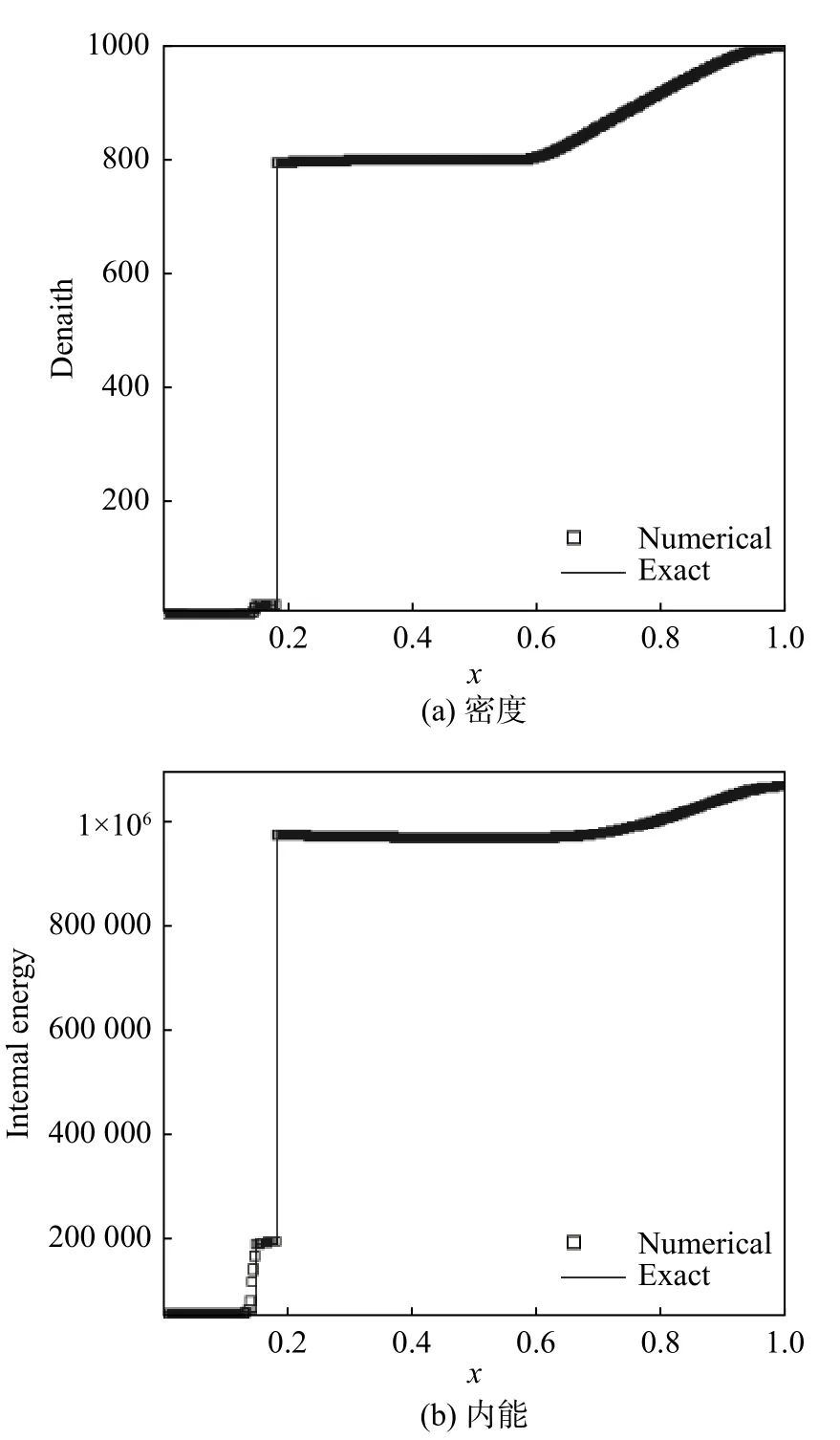
图4 t=0.000 24时的数值解

算例3 高压气泡爆炸问题

这是一个二维气−气多介质流问题。计算区域为[−1,1]×[−1,1]，其中充满静止的理想气体，中心处有一个半径为0.3的静止高压气泡。气泡内部的流体初始状态为：

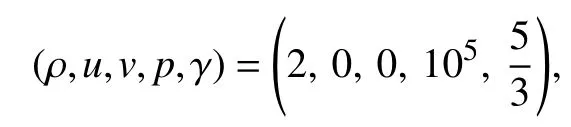
外部流体的初始状态为：

该问题中，气泡爆炸会产生一个向内的稀疏波，使得内部的密度与压力值急剧减小。图5、图6给出了网格数为200×200，t=0.000 7时刻的数值结果。可以看到，本文算法保证了结果的正确性，且能准确的追踪到介质界面。

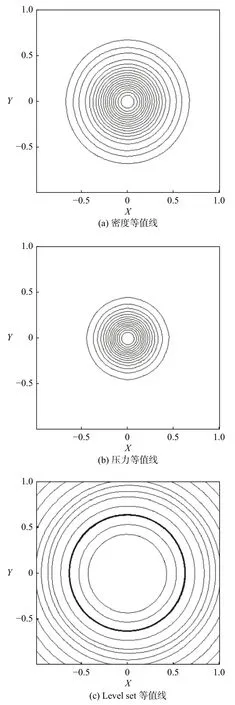
图5 t=0.000 7时的等值线图

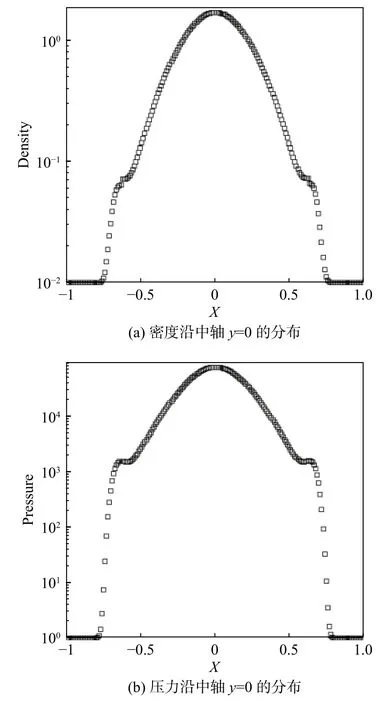
图6 沿中轴线y=0的数值解

4 结 论

针对一些极端条件下的多介质流问题，会因算法等误差导致出现不合理负值的情况，本文给出了一种具有正保护功能的求解方法。该方法首先使用具有正保护功能的双激波近似黎曼问题求解器求解黎曼问题，并用得到的近似解对界面附近的真实和虚拟流体状态进行重定义。接着在分别对各单介质流体进行求解时，将针对理想气体的正保护WENO算法推广运用于液体，从而得到了一种高精度正保护数值算法。最后通过数值算例验证了该算法能有效保正结果的正确性，且分辨率高，能准确捕捉到各类间断。