基于双层Kriging元模型算法的多产消代理商主从博弈能量管理模型

孙国强，王善磊，陈 胜，吴 晨，，胡国伟，周亦洲，卫志农

（1. 河海大学 能源与电气学院，江苏 南京 211100；2. 国网江苏省电力有限公司经济技术研究院，江苏 南京 210008）

0 引言

构建低碳可持续能源系统已成为国际社会推动能源转型、促进减少污染气体排放、应对全球气候变化的普遍共识和一致行动。在碳达峰和碳中和背景下，由于分布式能源的优势逐步显现，能源供给模式开始由集中式向分布式转型，终端用户的角色也逐步由消费者升级为产消者。2017年11月，国家发改委、国家能源局发布了《关于开展分布式发电市场化交易试点的通知》，产消者作为新兴主体参与市场化交易有了政策支撑［1］。然而，以产消者为代表的用户侧独立主体在参与市场交易时不可避免地面临以下问题：①受到自身容量限制，产消者单独参与电力现货市场交易时缺乏市场竞争力；②产消者多位于系统末端，电网对其不可观，因此难以被准确地调控［2］。在此背景下，产消代理商的概念应运而生。

产消代理商本质为面向产消者的能源聚合商，能够实现对不同类型产消用户的有效聚合，使其具备市场准入资格。目前，针对产消者及其代理商的市场交易以及优化调度问题已有较多研究，文献［3］研究产消者的日前优化调度问题，并且基于交互式能源机制建立了产消者的分布式调度框架。文献［4-5］研究多产消者基于合作博弈的日前调度策略，并分别基于Shapley 值法以及纳什谈判法实现合作剩余的公平分配。文献［6］研究产消者的需求响应模型，建立产消者与消费者之间的主从博弈模型。然而，上述文献仅对产消代理商的集中交易策略进行研究，仅考虑产消代理商与外部电网的单一交互关系。而实际上，由于多个代理商的用电行为以及用电模式具有良好的互补特性以及交互关系，因此对其交易策略的研究应该逐渐向产消代理商之间协调发展。文献［7］提出了一种基于分布式算法的产消者点对点多边竞价模型，并以智能合约的形式规定了产消者在点对点交易过程中的权利和义务。文献［8］则将产消者之间的能源交易问题转化为非合作博弈问题进行求解，进而以纳什均衡解作为最佳交易策略。

本文在产消代理商参与集中交易的基础上，同时考虑各产消代理商之间的分散式电能共享，并引入市场运营商MO（Market Operator）作为产消代理商与上级电网之间交易的过渡层，建立MO 与多产消代理商主从博弈优化模型，并以电价作为激励手段引导各产消代理商调整自身能量管理策略，提高彼此间的共享电量。然而，考虑到产消者聚合单元的多样性，能量管理模型中将不可避免地出现如燃气轮机启停、电动汽车EV（Electric Vehicle）充放电状态等布尔变量，导致能量管理模型非凸，无法推导其等效KKT（Karush-Kuhn-Tucher）条件，进而无法以计算速度较快的解析法对其进行求解。除解析法外，文献［9-10］提出了迭代循环的求解方法，但需要频繁调用上下层模型，求解效率过低。

Kriging 元模型为求解该问题提供了新的思路。由于对非线性模型具有良好的近似能力以及误差估计能力，Kriging 元模型经常被选作近似替代复杂仿真模型的简化数学模型，如文献［11］采用Kriging 元模型替代复杂的混合整数非线性模型，文献［12］采用元模型算法求解复杂的混合储能优化配置问题，文献［13］则将Kriging 元模型用于替代虚拟电厂的能量管理模型。本文在文献［11-13］的基础上，进一步采用双层Kriging 元模型替代下层产消代理商的能量管理模型，并在误差估计中引入低可信度代理模型，从而能够正确反映高可信度函数的变化趋势，显著提高误差估计精度，同时提高模型的训练速度以及拟合能力［14］。

综上所述，本文首先介绍了产消代理商的基本概念、基本特性、分类方法、运行框架及与其他能源服务商的区别；其次，考虑到不同产消代理商之间较大的电能互补潜力，构建了MO 与多产消代理商之间的主从博弈优化模型，剖析了MO 的动态定价策略及其与产消代理商运行策略之间的相互影响，并通过电价积极引导产消代理商之间的电能共享；最后，引入双层Kriging 元模型算法拟合替代下层非凸的产消代理商能量管理模型，实现主从博弈模型的高效求解。算例验证了本文所提方法的有效性。

1 产消代理商的概念

随着市场环境的不断开放，兼具电能生产和消费能力的产消者将作为新型利益主体参与市场运行。在此背景下，以先进的自动化技术、智能量测技术以及实时通信技术作为技术支持，对配电侧不同类型产消者进行整合，形成集电能生产和消费于一体、具有自主决策能力的聚合商——产消代理商，其含义可理解为集群化的产消者，因此具有源荷双重属性，且具有电力与信息高度融合与交互、对“价值”信号高度敏感等特点，其概念示意图见附录A图A1。

1.1 产消代理商的基本特性

在交互能源机制下，角色多重性、用户多样性以及交互性是产消代理商区别于其他能源服务商的基本特性［15］。角色多重性，即产消代理商兼具电力消费者以及生产者双重角色，且其身份可以在两者之间转换或同时兼顾；用户多样性，即产消代理商的种类、优化策略、效用度量指标以及能量交互机制的多样性；交互性，即产消代理商具有良好的主观能动性，并体现在产消代理商之间、产消代理商与上级运营商之间的互动过程。

1.2 产消代理商的市场运行机制

参考北欧电力市场运行机制，本文构建的产消代理商分层管理框架如图1 所示。从图中可见，各产消代理商隶属于第三方主体，其内部含有能量管理系统（EMS）等计算资源。在日前调度过程中，各产消代理商的能量管理系统结合内部产消用户的资源功率以及预测信息，制定可控资源的产用能计划，并上报其期望参与共享以及与电网交互的功率。产消代理商的上级运营商记为MO，其主要承担产消代理商与上级电网能量互动的过渡层作用，同时MO为盈利性的机构，拥有电力零售权，可制定与产消代理商的交易电价，并按照电网电价以及上网电价与电力市场进行交易，利用两者之间的差价来获取收益。

图1 产消代理商分层管理框架Fig.1 Hierarchical framework of prosumer aggregators

1.3 产消代理商与其他能源服务商的区别

产消代理商与其他能源服务商的区别和联系如附录A 表A1所示。在聚合单元层面，产消代理商本质上是对不同产消者用户的聚合，并对产消者内部聚合的分布式电源、储能等资源进行整合；而虚拟电厂是从区域配电网层级聚合分布式电源以及储能资源。在地域特性以及整体规模方面，产消代理商整体规模较小，对外整体呈现源荷双重属性；而虚拟电厂是聚合不同节点处的分布式能源，聚合规模较大，且一般对外呈现电源特性。在市场参与方面，产消代理商间的交易一般适用交互能源机制，即除了集中交易外，还可以通过点对点或能量共享的形式进行分散式交易，且点对点交易是自发进行的，与文献［16］提出的在平台支撑下进行的产消者-平台-产消者形式也有所不同。

1.4 产消代理商的分类

各产消代理商按其社会特性及源荷特性，可大致分为工业型、商业型和居民型。其中，工业型产消代理商可调容量较高，属于“电源主导型”产消代理商，对外整体呈现出“电能盈余”状态；商业型产消代理商主要为聚合商业楼宇的代理商，负荷需求量较高，属于“负荷主导型”产消代理商，对外整体呈现“电能缺额”状态；居民型产消代理商主要聚合居民侧可控负荷资源，可控容量较小，更侧重用电的经济性和舒适性［15，17］。尽管居民型产消代理商也属于“负荷主导型”产消代理商，但是一般对外整体呈现“电能自平衡”状态。

从聚合单元的角度看，各产消代理商具有一定的重合性，但对外整体呈现的状态是相对确定的。如对于商业型产消代理商而言，若增加充电桩设施，虽然在某些时刻由于EV 放电可降低商业型产消代理商的购电需求，但从整体上看，不会改变商业型产消代理商的负荷主导特性以及电能缺额特性。因此，产消代理商的分类除了考虑聚合单元外，仍有必要从社会特性及对外整体呈现的源荷特性角度考虑。

2 MO与多产消代理商主从博弈模型

结合图1 可知，MO 为产消代理商市场交易的上级运营商，MO的电价制定将会决定产消代理商选择何种交易方式，而产消代理商的交易方式也会反过来影响MO 的电价制定，对比产消代理商和MO 的市场地位以及投资主体，可构建MO 与多产消代理商主从博弈模型，其博弈框架如图2所示。

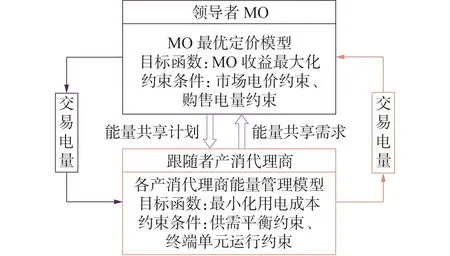
图2 本文构建的主从博弈框架Fig.2 Framework of proposed Stackelberg game

由图2 可见：MO 充当领导者角色，结合市场电价约束和购售电量约束，以最大化自身收益为目标制定各产消代理商的交易电价；各产消代理商作为跟随者，在接收到MO 的交易电价信息后，以最小化用电成本为目标优化内部各聚合单元的电量；MO则再次依据产消代理商的能量管理策略调整零售电价，从而形成领导者-跟随者顺次博弈，构成Stackelberg 博弈关系，而各产消代理商之间构成非合作博弈关系。

2.1 MO最优定价模型

MO 的效益函数为MO 参与现货市场获取的净利润，其中成本包括向上级电网和产消代理商购电支付的费用，收益包括向上级电网以及产消代理商售电的收入，具体如下：

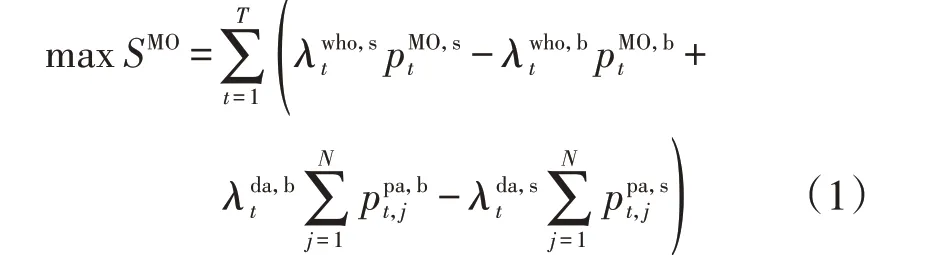
对于每个交易时刻，MO首先根据各产消代理商提交的购电量和售电量来确定共享电量，当电量盈余时将多余电量出售给上级电网，当电量缺额时从上级电网购入电量，因此有如下电量平衡约束：

2.2 不同类型产消代理商能量管理模型

2.2.1 工业型产消代理商

工业型产消代理商多聚合工业产消者，常见的聚合单元包含燃气轮机、电储能系统ESS（Electrical Storage System）、光伏机组等。工业型产消代理商整体对外呈现电源特性，其运行成本函数表示如下［19］：

2.2.2 商业型产消代理商

商业型产消代理商多聚合商业产消用户，主要可调资源为楼宇的中央空调系统CACS（Central Air-Conditioning System），运行成本函数如下：

进一步基于热力学方程以及智能楼宇的能量守恒原理，可得t时刻智能楼宇的室温时变方程为［20］：

2.2.3 居民型产消代理商

居民型产消代理商多聚合居民产消用户，常见的聚合单元主要包括EV 负荷、洗碗机、洗衣机等可转移负荷以及屋顶光伏，居民型产消代理商的运行效用函数表示如下：

洗衣机、洗碗机等可转移负荷可根据市场电价进行负荷转移，产消代理商需向参与负荷转移的居民支付一定的补偿费用，计算如下：

3 基于Kriging元模型算法的博弈模型求解

由于本文建立的主从博弈模型中下层产消代理商的能量管理模型涉及燃机轮机、EV 等布尔变量，导致下层模型非凸，难以获取其等效KKT 条件。而若简单采用智能算法对其进行迭代求解，则需要对下层模型进行频繁调用，严重影响模型的计算效率。因此，可考虑用元模型等效代理下层复杂的能量管理模型，而Kriging 模型由于对非线性模型具有良好的近似能力和误差估计能力，故本文选择Kriging 元模型作为下层产消代理商能量管理模型的代理模型，其数学原理见附录B，从而可将交易电价与交易电量之间的隐性映射关系简单显示，避免了对下层模型的频繁调用，实现模型的高效求解。

3.1 双层Kriging元模型

为提高Kriging 元模型的训练效率，本文进一步采用双层Kriging 元模型算法。该算法采用双样本池更新法，其中低置信度样本池用于反映样本点在更新过程中的整体变化趋势，高置信度样本池用于实际的数值结果拟合。采用双层Kriging 元模型后，可将交易电价和交易电量之间的隐性映射关系表示为：

式中：ΩMO为交易电价的可行域空间。

3.2 基于双层Kriging元模型的博弈模型求解流程

3.2.1 初始模型构建

3.2.2 模型在线修正

1）关键区域划分。

将3.2.1 节中生成的样本集Bj代入目标函数式（1）中，计算不同样本点对应的目标函数值SMO，并根据SMO的大小将MO 的策略空间划分为多个区域。通过不断缩小优质采样点的区间范围，逐步剔除含最优解概率较低的区域，从而实现各区域的并行计算，提高寻优效率。关键区域划分的方法和步骤见附录C。

2）双样本池更新。

双样本池更新思路如下：首先，在每个关键区域上，通过粒子群优化（PSO）算法结合拟合好的双层Kriging 元模型对优化模型（式（30））进行寻优，快速锁定该区域内的最优交易电价和交易电量，尽管此时的交易电量并非真实值，但是该样本点反映了上一轮电价-电量之间的拟合趋势，一定程度上反映了目标函数的变化趋势，故将其放入低置信度样本池中；然后，将上述最优电价作为已知量，代入下层产消代理商的能量管理模型中，计算实际最优交易电量，此时得到的交易电价-电量为真实值，可作为数值拟合的样本点，将其加入高置信度样本池中。

3.2.3 模型求解步骤

基于双层Kriging 元模型算法的主从博弈模型的详细求解流程如附录D图D1所示，具体如下。

步骤1：输入基本参数，构建初始训练样本集。

步骤2：构建初始双层Kriging元模型。

步骤7：判断前后2次迭代全局最优解是否满足收敛条件，是则输出最优解，否则返回步骤2。

4 算例分析

4.1 算例数据

本文以一个MO 与3 类不同产消代理商构成的仿真算例验证所提方法的有效性。工业型产消代理商、商业型产消代理商和居民型产消代理商分别记为代理商1、代理商2 和代理商3。燃气轮机以及ESS的参数详见附录E表E1、E2。CACS的相关参数见附录E 表E3，智能楼宇建筑热参数见参考文献［20］。EV 的基本参数见附录E 表E4，各类型EV 的数量均为200 辆，EV 蓄电量上、下限分别为电池容量的95%和15%，最大充放电功率取为电池容量的20%，充放电效率为0.9。可转移负荷的补贴电价为50 €／（MW·h），最大可转移量为总负荷的5%，并规定负荷只能从用电峰值时段转移至非峰值时段，即允许负荷转移时段为11:00—15:00和18:00—20:00。各代理商光伏出力曲线以及负荷曲线见附录E 图E1、E2 。

本文采用PSO 算法对上层MO 动态定价问题进行优化求解，并采用YALMIP 工具包调用CPLEX 求解器对下层代理商能量管理模型进行求解，Kriging元模型的构建平台为MATLAB 中的DACE 工具箱。所有算例测试均在MATLAB 2017b软件上完成。

4.2 算例结果分析

4.2.1 MO动态定价与产消代理商优化结果分析

为体现MO 与多产消代理商之间通过主从博弈确定交易电价以及能量管理策略的有效性，本文设置以下2 种策略：策略1 为MO 不对电价进行优化，电力市场购售电价即为产消代理商与MO 的交易电价；策略2为MO采用主从博弈框架进行电价优化。

不同策略下，MO 的电价优化结果如图3 所示，MO 与上级电网的最终交易电量如图4 所示，代理商间的共享电量如附录F 图F1 所示。从图中可以看出，策略2 中MO 通过电价优化，显著增加了代理商间的共享电能，从而减少了MO 与上级电网之间的交易电量，提高了经济效益。

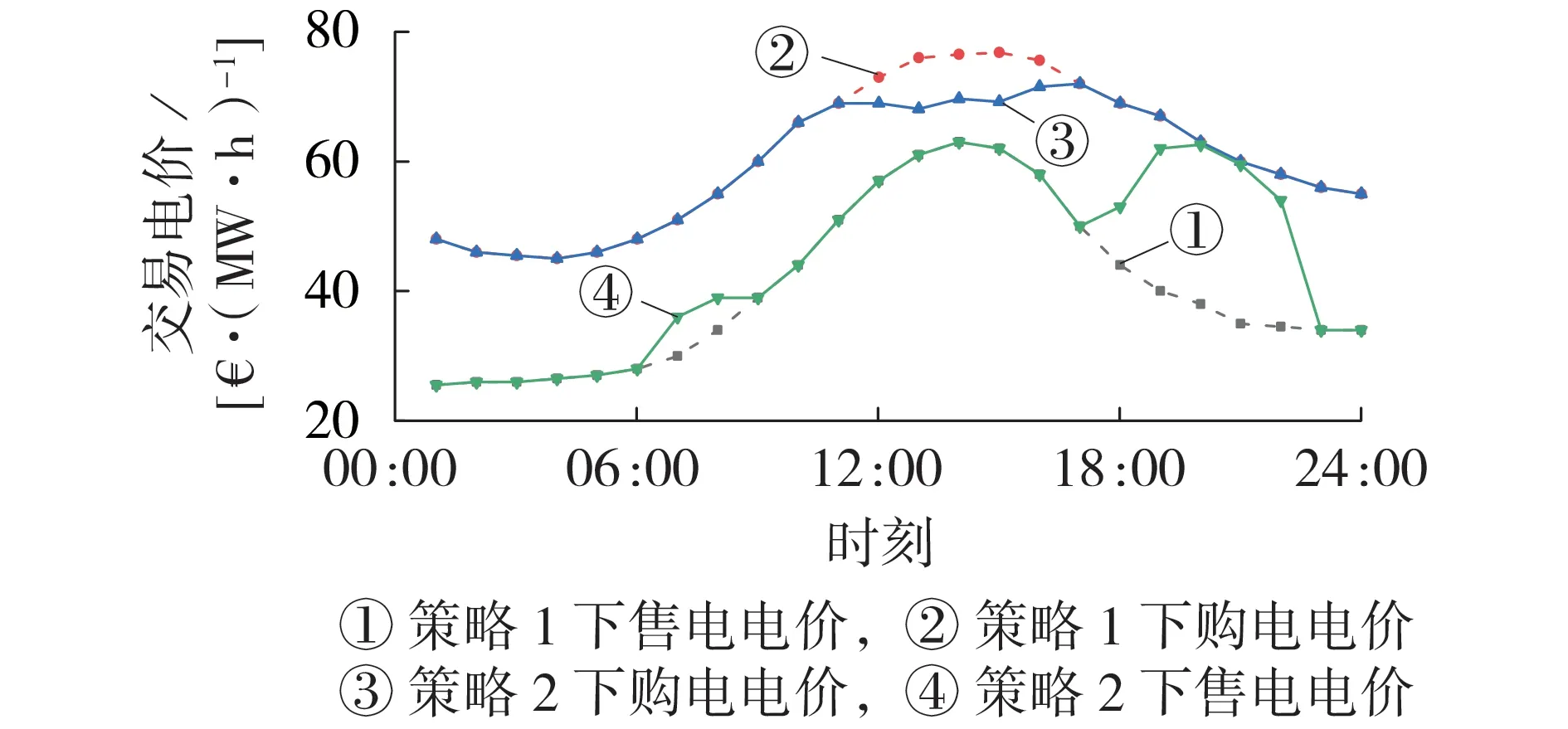
图3 不同策略下交易电价优化结果Fig.3 Optimization results of transaction price under different strategies

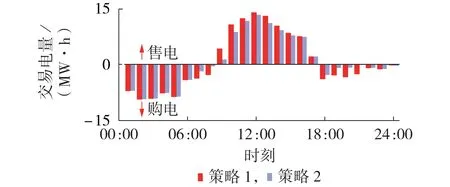
图4 MO与上级电网交易电量结果Fig.4 Trading electricity results between MO and superior power grid

各代理商的交易电量图见附录F图F2。由图可见：在01:00—05:00 时段，由于各代理商均供不应求，此时各代理商无法进行能量共享，MO 为保证不亏本，将产消代理商的购电电价定为电网的购电电价；在06:00—08:00和18:00—24:00时段，不同产消代理商的购售电策略不同，如在06:00—08:00时段，代理商1 处于向MO 售电状态，而代理商2 和代理商3 均需从MO 购电，总体来看，电能处于供不应求状态，MO需向上级电网购电以满足产消代理商的电量需求，此时MO 通过提高代理商售电电价吸引多电产消代理商出售更多电量以满足少电产消代理商的需求；在09:00—17:00时段，除代理商2外，代理商1和代理商3均处于向MO售电状态，整体处于供大于求状态，MO 降低此时代理商的购电电价，以减少向上级电网的出售电量，促使少电产消代理商以及自平衡产消代理商增加用电量，从而提高彼此间的共享电量。可见，产消代理商的运行状态会影响MO电价的制定，而MO 制定的电价亦可以引导各产消代理商调整各自的运行状态，增加彼此间的共享电量。

不同策略下，各代理商的运行成本以及MO 的整体收益变化如表1所示（负值代表成本）。

表1 不同策略下各主体收益Table 1 Income of each subject under different strategies

由表1可见，MO进行电价优化后，代理商1的经济收益和MO 的综合效益分别提高了732.40 €和408.68 €，代理商2、代理商3的运行成本也分别降低了96.47 €和183.90 €。可见，采用主从博弈框架对MO 进行电价优化能够显著提高MO 的经济效益，并能在一定程度上降低各产消代理商的运行成本。

4.2.2 多产消代理商互补特性及耦合作用分析

不同产消代理商对于整体电能共享的作用如图5所示。从图中可以看出：若不考虑代理商1加入联盟，整体共享电量相对较低；若不考虑代理商2 或代理商3 加入联盟，虽然整体的共享电能也有所降低，但是远不如不考虑代理商1 加入联盟降低得多。可见，本文考虑多类型产消代理商的能量共享能够充分利用不同产消代理商的时空互补特性，增加产消代理商间的共享电量，减少整体与上级电网的交互功率。

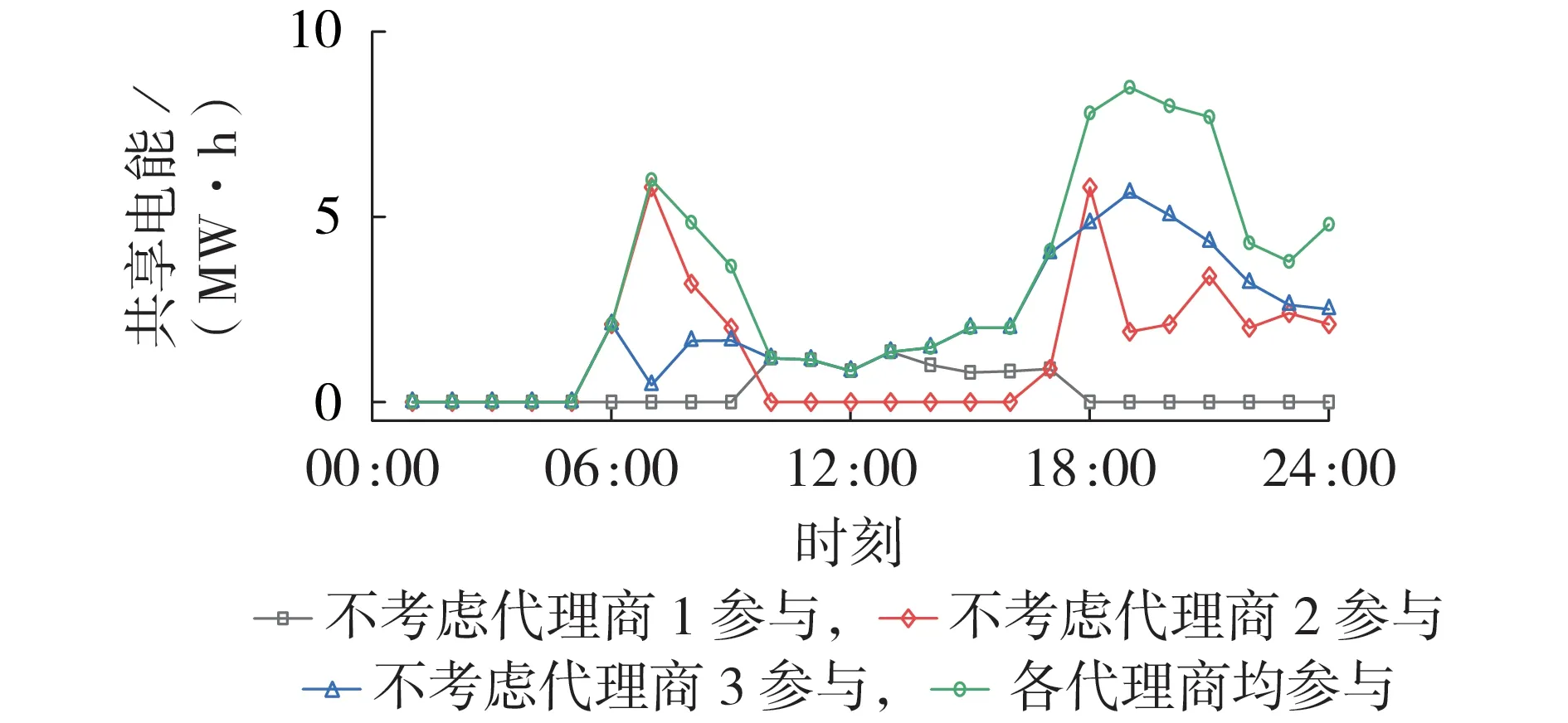
图5 不同场景下的共享电量结果Fig.5 Shared power results under different scenarios

具体到产消代理商聚合单元来看，以商业型产消代理商的CACS 为例，其在不同策略下的运行状态如图6所示。

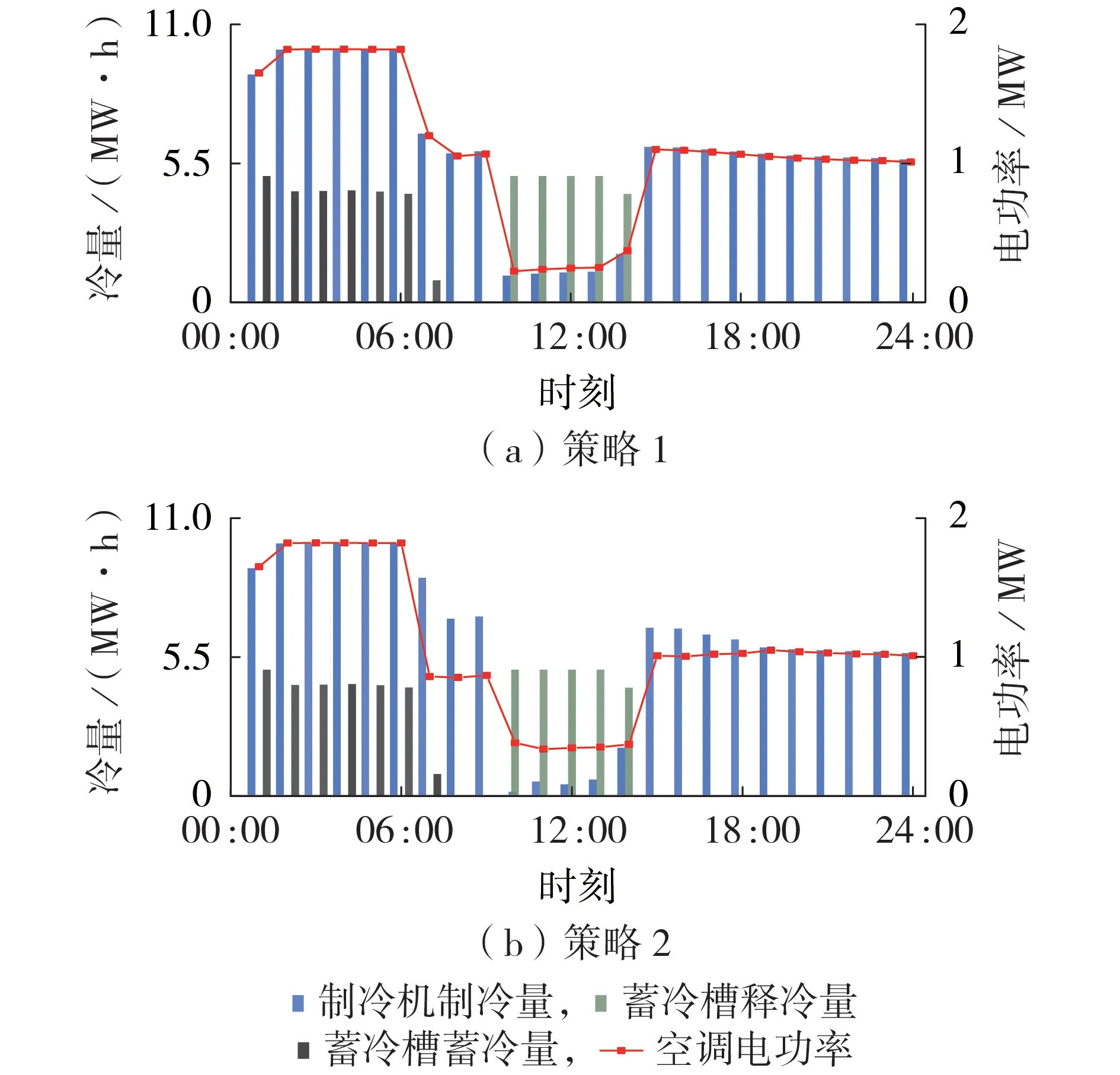
图6 不同策略下CACS运行状态Fig.6 Operation status of CACS under different strategies

通过对比可以看到：策略2 中CACS 在07:00—09:00和15:00—17:00时段耗电量有明显降低，这主要是因为MO 降低了售电电价并提高了购电电价，CACS为减少运行成本，在满足最低舒适度要求的前提下，减少电能的消耗；在10:00—14:00时段，MO通过降低购电电价吸引少电产消代理商多消耗电能，故此时CACS 耗电量较策略1 有明显增加。燃气轮机和EV 在不同策略下的运行状态分别见附录F 图F3和图F4。

4.2.3 双层Kriging元模型算法的有效性分析

为测试不同算法的性能，本文对双层Kriging 元模型、单层Kriging 元模型和传统迭代算法（PSO 算法）进行了系统性的测试。图7为某次计算过程中3种算法的收敛过程图，表2 为取10 次计算结果的平均值。

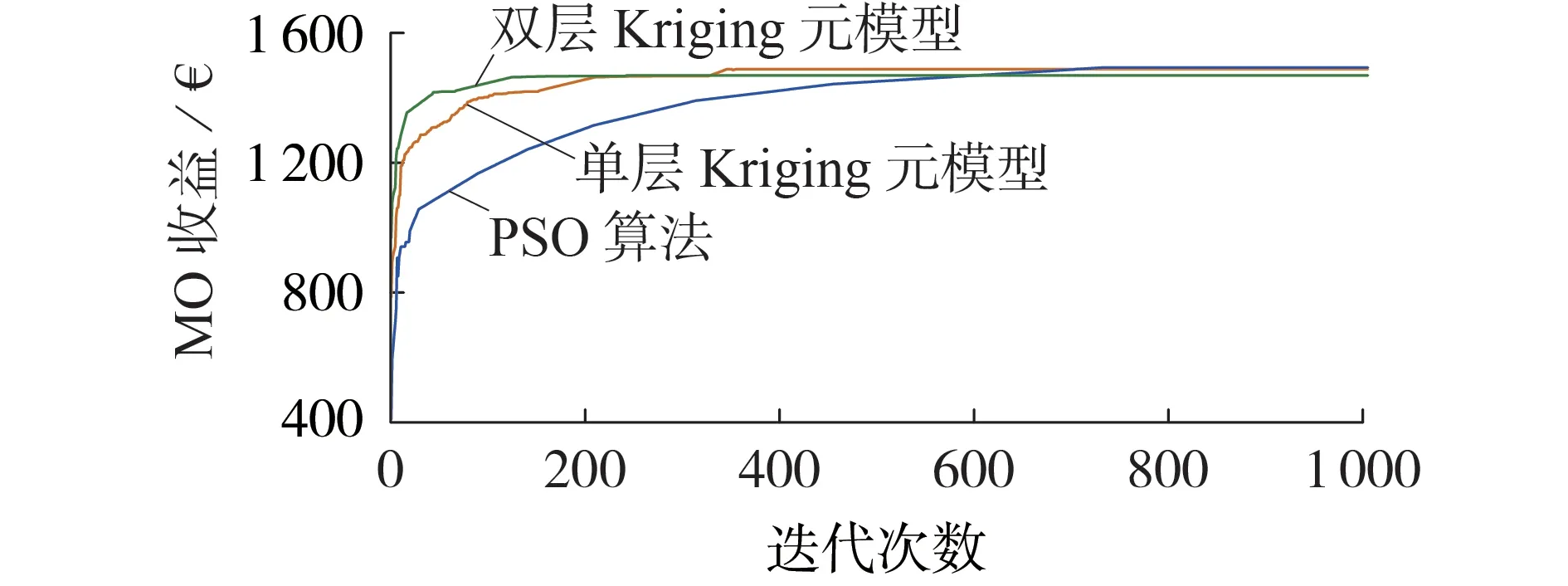
图7 不同算法收敛过程Fig.7 Convergence process of different algorithms

表2 不同算法性能测试结果Table 2 Performance test results of different algorithms

从图7 中可以看出，3 种算法最终得出的MO 运行收益相差不大，但是不同算法的收敛过程和收敛速度差别较大，2 种Kriging 元模型算法的整体收敛速度更快，双层、单层Kriging 元模型算法分别在约180 次和350 次迭代后收敛，其效率远高于传统PSO算法。

由表2可知，3种算法的下层模型调用次数和总计算时间存在明显差异性。由于PSO算法每一步粒子的更新均需要对下层模型进行调用求解，当粒子数量较多时，对下层模型的频繁调用将带来严重的“维度灾难”。与PSO 算法相比，2 种Kriging 元模型算法均能够大幅度减少对下层模型的调用次数，有效提高计算效率。并且，相比单层Kriging元模型，双层Kriging 元模型对下层模型的调用次数更少，计算时间减少了26%，这主要得益于双层Kriging 元模型更强大的数据拟合能力和更高效的样本训练机制。

2种Kriging 元模型的收敛过程如附录F图F5所示。可见，双层Kriging 元模型整体的误差要小于单层Kriging 元模型，在低置信度代理模型的作用下，其整体误差在迭代开始时也较小，且收敛速度较单层Kriging元模型更快。

产消者数量增加对于模型求解时间的影响见附录F表F1。可以看出，随着代理商数量的增加，模型总的迭代次数变化并不明显，计算时间的增加速度也较为缓慢，并非呈类似指数型的爆炸式上升，可见本文所提算法对于复杂系统环境依然适用。

5 结论

本文提出一种MO 和多产消代理商的主从博弈模型，并采用一种双层Kriging 元模型算法实现模型的高效求解。算例结果表明：

1）通过本文所构主从博弈模型对产消代理商购售电价的优化，能够增加产消代理商间的共享电量，有效减少MO 与上级电网的交易电量，提高MO 及各产消代理商的经济效益；

2）双层Kriging 元模型算法在保证计算结果正确的前提下，有效减少了模型的迭代次数，显著提高了模型的求解效率。

随着用户侧市场的不断开放，本文所构建的主从博弈模型能够适应小规模的分布式发电交易，使市场中的主体可以积极自主地寻求交易，通过市场化的手段达到不同资源优化配置。在后续研究中，笔者将进一步探索基于合作博弈、非合作博弈等手段的产消代理商集中-分散交易方式，并对产消代理商内部产消者的合作剩余分配进行深入研究。

附录见本刊网络版（http：//www.epae.cn）。