基于全局灵敏度的区间模式阻尼提升策略
2021-11-20杨德友王丽馨
杨德友,赵 康,王丽馨
(东北电力大学 电气工程学院,吉林 吉林 132012)
0 引言
随着大规模能源基地和大容量传输通道的建设和投产,电力系统的小干扰稳定问题愈加突出,尤其是由弱阻尼引起的低频振荡问题,给电力系统安全稳定运行带来了潜在威胁[1]。
目前,有改变电网结构、增强闭环控制设备以及改变运行方式[2-3]这3种抑制低频振荡的常用控制手段。前2 种控制手段对本地振荡模式抑制效果明显,而对区间振荡模式的抑制效果有限[4]。改变运行方式可以通过改变发电机有功功率输出来提高区间振荡模式阻尼,基于有功调节的阻尼提升策略中有2 个主要的环节,分别是确定机组有功调制量和选择参调机组。关于有功调制量的确定,目前的研究主要采用试探法,经过多次调节使系统阻尼提升到满足安全运行要求[5]。针对参调机组的选择,当前的研究主要通过计算特征值灵敏度来实现,但对于大型系统,特征值提取存在“维数灾”的问题,因此难以在线应用[6-7]。文献[8-10]提出了基于广域量测信息的低频振荡控制措施,通过计算各机组的参与因子或特征值灵敏度实现机组筛选,可以实现在线应用,但该方法对数学模型的准确性要求极高。文献[11]提出了基于随机数据的局部灵敏度算法,利用虚拟状态矩阵代替特征值的求取过程,解决了对数学模型准确性要求高的问题,但该算法只能反映某台机组有功出力变化对阻尼的影响程度。而在实际系统中,小幅环境激励下系统全部发电机有功出力都是时刻变化的,因此通过该方法得到机组排序的准确性受到影响。
为了克服上述局部灵敏度的缺陷,将基于概率分布的全局灵敏度分析方法引入阻尼比灵敏度计算中,以此作为参调机组的选择依据。该方法能够定量分析各输入参数同时变化时对系统输出参数的影响,并得到对系统输出影响较大的重要输入变量。全局灵敏度分析方法主要包括多元回归法、傅里叶幅值检验扩展法和Sobol’法[12-13]。目前,Sobol’法作为基于方差的全局灵敏度分析方法被逐渐应用于电力系统的关键参数辨识中[14-16]。
本文在研究基于Sobol’法计算全局灵敏度的基础上,以负荷小幅随机波动下系统随机响应为数据源,提出了用于选取参调机组的全局灵敏度分析方法。考虑发电机组功率调整限额并结合定向试探法确定发电机有功调制量,在此基础上设计了基于发电机有功定向调制的区间模式阻尼提升策略,实现了区间弱阻尼模式阻尼比的快速提升。IEEE 2区域4机系统和IEEE 5区域16机系统的仿真结果验证了本文方法在消除系统潜在的不安全模式、提升系统阻尼比方面具有较好的效果。
1 随机数据驱动的特征参数辨识
基于发电机侧相量测量单元(PMU)的广域测量系统(WAMS)可以实时地提取发电机及网络中的动态信息,例如功率、频率和相角等,提取的动态信息可以作为电网安全分析的基础量测数据。通常对电网进行安全分析主要是将故障后具有明显波动特性的量测数据提取出来,然后利用小信号稳定分析、线性化处理等方法对提取的量测数据进行分析,得到系统安全分析的结果。然而在实际电力系统运行中,当系统没有大的扰动时,测量得到的系统响应表征为凌乱的类似噪声的随机响应信号,文献[11]的研究表明系统的动态特性信息包含在环境信号激励下系统的随机响应中。基于随机响应数据的安全分析方法主要是利用系统的辨识理论,构造出虚拟状态矩阵,该虚拟矩阵包含系统的动态特性,并对虚拟状态矩阵进行特征分析,通过辨识得到系统模态参数分析系统机电振荡特性。目前,应用比较广泛、比较成熟的技术是随机子空间辨识(SSI)算法。
在电力系统中,经过PMU 测量得到的数据在时间上是离散的,经过采样之后得到系统的状态空间模型为:

式中:xk′∈Rn为状态变量;yk′∈Rl为系统输出变量;wk′∈Rn、vk′∈Rl为假定白噪声,且其期望值分别为E(wk′)=0、E(vk′)=0;Ad∈Rn×n为离散系统状态矩阵,Ad=eAcΔt,Ac∈Rn×n为连续系统状态矩阵,Δt为采样时间间隔;C∈Rl×n为系统输出矩阵。
SSI算法的详细过程参见文献[17],主要的步骤包括以下5 个方面:①将量测数据提取出来构造Hankel 矩阵;②对Hankel 矩阵进行LQ 分解;③对分解以后得到的下三角矩阵进行奇异值分解;④计算延伸可观察矩阵;⑤得到离散系统状态矩阵Ad及系统输出矩阵C。
在确定Ad后对其进行特征值分解:

式中:αi、βi分别为特征值的实部和虚部。则振荡频率fwi及阻尼比ζi分别为:

本文将PMU 测量得到的发电机有功功率作为随机响应输入数据,进而利用SSI 算法对随机测量数据进行辨识,得到电力系统各振荡模式所对应的频率、阻尼比和模态等特征信息。
2 全局灵敏度分析
2.1 全局灵敏度指标
通过仿真等措施建立数学模型,是解决复杂问题的主要方法。但在实际系统中存在大量的随机性参数,且每个参数对系统输出响应的影响也各不相同,参数的灵敏度反映了输入参数变化对系统输出响应的影响程度。本文采用基于Sobol’法的全局灵敏度分析方法对系统参数进行分析,其本质为一种基于方差理论定量评估系统全局灵敏度的方法,可以分析单个输入变量或多个输入变量的共同作用对系统输出的影响程度,下面介绍Sobol’法的基本理论。
在空间Ωk上定义解析函数f(x),其中,输入随机变量x=[x1,x2,…,xk],为不失一般性,Ωk可表示为:
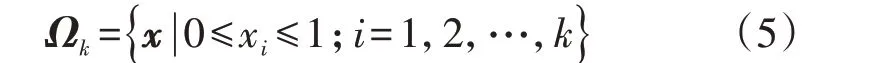
式中:k为输入随机变量参数的个数。将函数f(x)分解为2k个递增项之和:

由式(7)可知,式(6)中所有分解项之间都是正交的,并且可通过函数f(x)的积分形式得到:
式中:x~i表示排除输入随机变量xi之后其余的输入随机变量,同理x~ij表示排除输入随机变量xi和xj之后其余的输入随机变量。
将式(6)等号左右两边分别在整个定义域内平方并积分可得:
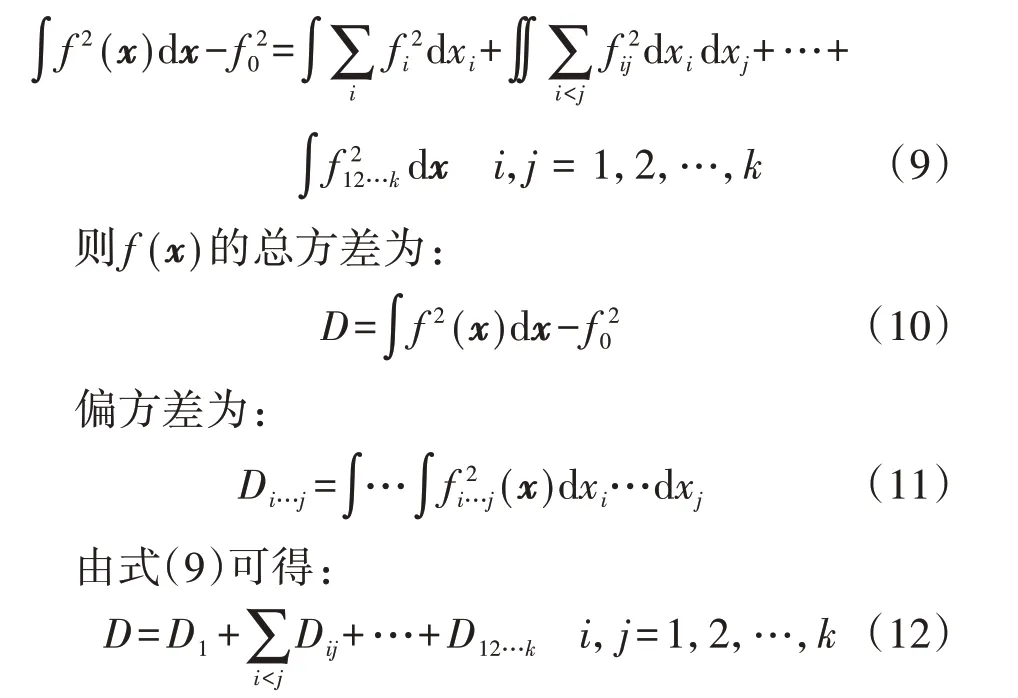
最后得到输入随机变量的灵敏度为:

式中:Si为第i个参数的一阶灵敏度指标(FSI);Sij为二阶灵敏度指标;STi为总灵敏度指标。本文以Si作为全局灵敏度指标进行分析计算。
2.2 全局灵敏度指标计算
对一个实际系统进行分析时,通常用解析函数f(x)来描述这个系统的特征,即输入变量与输出变量对应的关系,f(x)通常是比较复杂的,求解f(x)比较困难,或者当函数的解析式无法获得时就无法通过求解f(x)得到输入变量对应的输出结果。在这样的背景下,基于Sobol’法的全局灵敏度分析方法具有一个突出的优点,在无法获得函数的解析式时或者获得的解析式非常复杂时,可以通过蒙特卡罗模拟(MCS)方法计算式(10)、(11)的积分,从而得到Si。其步骤如下。
1)通过PMU数据量测得到一个随机矩阵P:
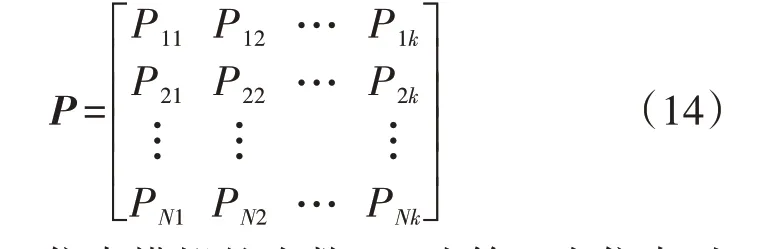
式中:N为MCS仿真模拟的次数;PNk为第N次仿真时第k台发电机输出的有功(本文以各台发电机有功输出功率作为随机输入变量)。
2)以生成矩阵P同样的方法生成一个N×k维的随机矩阵H,将矩阵P的第i列替换为H的第i列,得到k个新的矩阵Hi(i=1,2,…,k)。
3)根据输入随机矩阵P和Hi,通过SSI得到弱阻尼区间模式对应的阻尼比,计算对应的输出矩阵fP和fHi(i=1,2,…,k),将该阻尼比作为系统的输出。矩阵P、Hi的输出矩阵fP、fHi维数均为N×1,则式(10)、(11)的估计值D̂i、D̂i…j为:

式中:f j P、f j Hi分别为输出矩阵fP、fHi的第j个元素。
4)进一步计算可以得到FSI的估计值Ŝi为:
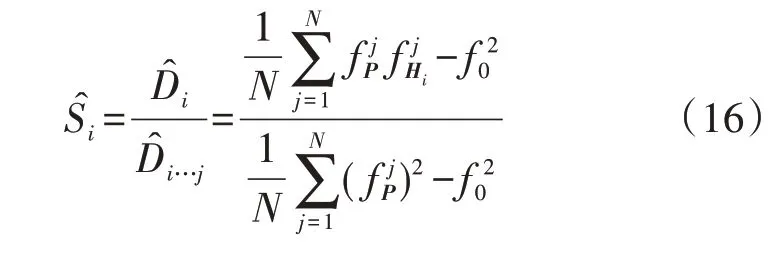
通过上述计算可以得到评估输入变量对系统输出的影响程度,即发电机有功输出对系统弱阻尼区间模式对应阻尼比的影响程度,得到各发电机输出有功参数的一阶灵敏度指标。具体流程见附录A图A1。
3 基于全局灵敏度的发电机有功调制方案
3.1 基于全局灵敏度的参调发电机筛选
对于互联电力系统,区间联络线传输有功功率与其对应的区间模式阻尼具有强相关性,且满足区间模式阻尼随着区间传输功率的增大而减小、随着区间传输功率的减小而增大的关系。本文提出的基于发电机有功调制的互联电网阻尼提升策略,通过减小送端区域发电机有功输出同时增加受端区域发电机有功输出,可以降低系统区间联络线传输功率,从而实现区间模式阻尼的有效提高。
根据2.2节所提全局灵敏度指标计算方法,全局灵敏度指标只能反映发电机有功输出对系统弱阻尼区间模式对应阻尼比的影响程度,不能给出发电机组有功功率调制具体的调节方向信息。为了防止由FSI筛选得到的发电机来自于同一个调节机群,在进行参调机组筛选之前,先根据振荡模态的辨识结果,获取参与振荡的机组大致的振荡分群信息,并依据区间潮流方向确定两群机组的出力调整方向,从而确定送端区域机组和受端区域机组。
在机组分群确定之后,依据全局灵敏度指标大小对送端区域和受端区域中参调机组进行排序,即按照送端区域中全局灵敏度指标大小对机组进行有功下调优先级排序,按照受端区域中全局灵敏度指标大小对机组进行有功上调优先级排序。进而,送端区域机组按照灵敏度指标排序下调有功出力同时受端区域机组按照灵敏度指标排序上调有功出力,提升系统阻尼水平。
3.2 发电机有功调制量的确定
对于改变发电机有功功率来提升系统阻尼的控制手段,传统的有功调整方法是根据给定的有功调制量,以各台发电机阻尼灵敏度数值的大小作为指标,按指标权重给各台发电机分配有功调制量,这样操作的结果会导致较多的发电机都参与有功功率调制,但是在实际的电力系统调度中希望以有功调制机组最少来实现系统稳定。为此,本节以有功调制机组最少为原则,应用定向试探法完成发电机有功调制量的确定,具体步骤如下。
1)构造有功调制发电机组合{Gs,Gr},其中发电机Gs、Gr分别为下、上调机组中全局灵敏度指标最大的发电机。
2)按照送端机组有功功率下调、受端机组有功功率上调的原则,分别计算发电机Gs的有功下调量和Gr的有功上调量,如式(17)、(18)所示。

式中:PGs为Gs的有功输出功率;PGsmin为Gs的有功调制量下限值;PGr为Gr的有功输出功率;PGrmax为Gr的有功调制量上限值。
3)对ΔPGs、ΔPGr进行对比,选取较小的有功调制限值作为有功调制量,如式(19)所示。
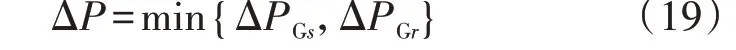
3.3 基于发电机有功定向调节阻尼提升策略
本文以发电机有功随机响应为数据基础,利用SSI 算法辨别系统的特征参数,进而判断系统是否存在区间弱阻尼模式,若存在区间弱阻尼模式,即区间模式阻尼比小于5%,则通过全局灵敏度辨别各发电机有功功率变化对区间阻尼比的影响程度,求得各台发电机输出有功功率的全局灵敏度指标。然后根据全局灵敏度指标大小对送受端区域机组中的发电机进行参调优先级排序,进而利用3.2节所提方法实现有功调制量的确定,并重新利用SSI 算法辨识系统特征参数并判断系统是否存在潜在威胁,若存在,则退出有功调制限值为0 的发电机,按照上述过程重新筛选发电机组并实现有功调制,流程图见图1。

图1 发电机有功定向调制流程图Fig.1 Flowchart of generator active power directional redispatch
4 仿真分析
4.1 IEEE 2区域4机系统
本节以IEEE 2 区域4 机系统为例,对提出的基于全局灵敏度区间模式阻尼调制策略进行仿真验证。系统结构如附录A 图A2所示,系统参数参见文献[18]。为了模拟实际系统的负荷波动,本文假设节点4、14 处的负荷以其基础值的5% 随机波动。利用SSI 算法对系统频率、阻尼比进行在线辨识,并与传统小干扰稳定分析方法的理论值进行对比,如表1所示。

表1 SSI算法计算值与理论值对比Table 1 Comparison between calculative values of SSI algorithm and theoretical values
由表1 可知,利用SSI 算法得到的频率和阻尼比与理论值相近,并且系统中存在一个阻尼比仅为3.18%的弱阻尼区间模式。当阻尼比小于5%时,电力系统稳定性受到潜在威胁。为了防止受扰后电力系统产生持续的低频振荡,需采取措施将弱阻尼区间模式的阻尼比提高至5%及以上。
在进行有功调制之前,首先确定送、受端区域机组,根据相对振荡发电机组在模态图中的分布信息,对振荡发电机进行分群,弱阻尼区间模式的振荡模态辨识结果如图2 所示。由图可知,发电机G1、G2构成的机群相对于发电机G3、G4构成的机群振荡程度较大。在机组分群结果基础上,并结合区间潮流方向信息,确定系统送端机组为G3、G4,受端机组为G1、G2。

图2 振荡模态辨识结果Fig.2 Identification results of oscillation modes
利用第2 节提出的全局灵敏度分析方法,辨识各台发电机输出有功功率对弱阻尼模式阻尼比的影响程度,通过计算得到各台发电机有功功率的全局灵敏度指标分别为SG1=0.262 7、SG2=0.311、SG3=0.512 3 和SG4=0.315。依据各台发电机所对应的全局灵敏度指标的大小,然后结合送端机组有功功率下调、受端机组有功功率上调的原则,得到有功功率上调机组的排序为G2、G1,有功功率下调机组的排序为G3、G4。为了验证本文全局灵敏度分析方法的正确性,比较利用全局灵敏度算法与传统特征值灵敏度算法计算得到的结果,对比结果如图3所示。
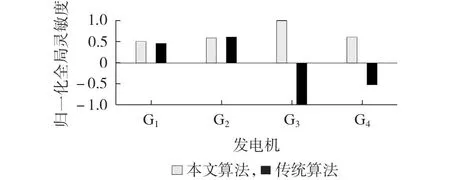
图3 全局灵敏度算法与传统特征值灵敏度算法对比Fig.3 Comparison between global sensitivity algorithm and traditional eigenvalue sensitivity algorithm
分析图3 中的结果,传统特征值灵敏度的正负号仅代表发电机有功的调制方向,在已知发电机属于送端或受端的前提下,发电机有功的调制方向已确定,因此本文提出的全局灵敏度计算结果与传统特征值灵敏度计算结果表示的影响程度基本一致,进而为本文所提方法的正确性提供了依据。
在初始状态下,系统的频率以及阻尼比分别为0.6305 Hz、3.18%。利用3.2节所提方法确定有功调制量,根据全局灵敏度指标的计算结果和送受端区域机组的判定结果,得到第一次调制的发电机组合为{,}(上标“+”、“-”分别表示发电机有功功率上调、下调,后同),然后根据G2、G3的有功输出功率与功率调制限值得到有功调制量为ΔP1=1.5 p.u.。将G2的有功功率上调1.5 p.u.,G3的有功功率下调1.5 p.u.,并计算调制后系统区间模式阻尼比,其值提高到4.24%,仍小于5%,继续执行调制过程,由于G2达到有功调制上限后退出调制,第二次调制的发电机组合为{,},有功调制量为ΔP2=1.12 p.u.,调制后阻尼比提高到5.01%,满足系统安全运行要求,调制结束,调制结果如表2 所示,表中有功调制量为标幺值,后同。

表2 IEEE 2区域4机系统发电机调制结果Table 2 Generation modulation results of IEEE 2-area 4-machine system
调制过程中发电机有功功率和区间模式阻尼比的变化过程如图4 所示。图中,G1—G3有功输出功率PG1—PG3为标幺值,后同;ξTH、ξID分别为阻尼比的理论值、辨识值。
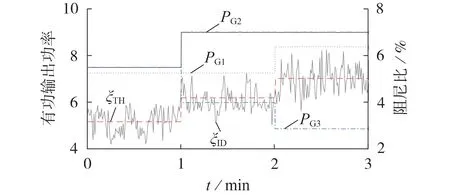
图4 发电机有功输出功率和区间模式下阻尼比波形Fig.4 Waveforms of generation active output power and damping ratio under interval mode
4.2 IEEE 5区域16机系统
IEEE 5 区域16 机系统接线图如附录A 图A3 所示,该系统分为5个区域,共68个节点。在系统负荷处添加其基础值5%的随机扰动信号,然后利用SSI算法对系统区间模式特征参数进行在线辨识,特征参数辨识结果见表3。

表3 SSI算法下低频振荡特征参数的辨识结果Table 3 Identification results of low frequency oscillation eigen parameters under SSI algorithm
由表3可知,系统中一共有3个强阻尼区间模式和1 个弱阻尼区间模式,其中弱阻尼区间模式的振荡频率为0.538 9 Hz,阻尼比仅为1.87%,并且由附录A 图A4 所示弱阻尼区间振荡模态辨识结果可得与弱阻尼模式相关的发电机分群信息为{G1—G9}、{G10—G13}。
采用3.1 节提出的全局灵敏度分析方法计算得到各台发电机的全局灵敏度指标,为了定量观察各灵敏度指标对区间弱阻尼的影响程度,对灵敏度指标进行归一化处理,结果如图5所示。依据图5中各台发电机所对应的全局灵敏度指标的大小,结合弱阻尼区间振荡模态的辨识结果并依据区间潮流方向信息,得到有功功率下调机组的排序为G5、G6、G4、G3、G7、G8、G2、G9、G1,有功功率上调机组的排序为G12、G11、G13、G10。

图5 发电机归一化全局灵敏度指标Fig.5 Normalized global sensitivity index of generator
利用3.2节所提方法确定有功调制量并利用3.3节提出的调制策略提升IEEE 5 区域16 机系统的区间弱阻尼模式的阻尼比。初始状态下,系统频率及阻尼比分别为0.630 5 Hz、1.87%。系统第一次调节之后,阻尼比提升到3.32%,第二次调节后,阻尼比提升到5.45%,消除了系统潜在威胁,调制结束,发电机有功调制的结果如表4 所示,调制过程中阻尼比及各发电机组有功输出调制变化过程如附录A 图A5所示。

表4 IEEE 5区域16机系统发电机调制结果Table 4 Generation modulation results of IEEE 5-area 16-machine system
在戴尔处理器为Inter Core i5-5200U,主频2.20 GHz,运行内存4 GB 的笔记本电脑上进行仿真分析和计算,以IEEE 5区域16机系统第一次发电机有功调制过程为例,分析所提阻尼提升策略的计算耗时情况,结果表明第一次调制所需时间约为62.3 s,包含SSI 特征参数识别所需时间2 s,同调机组识别所需时间0.1 s,全局灵敏度指标计算时间60 s 以及发电机有功再调度过程所需时间0.2 s。其中,全局灵敏度指标计算过程为主要耗时环节,约占调制过程总耗时的96%。一般,仅需要2~3 次有功调制即可提升系统阻尼水平至安全运行要求。因此,本文提出的有功调制策略的整体耗时约为2~3 min,满足在线应用要求。
5 结论
针对系统中潜在的区间弱阻尼模式,本文提出了一种基于全局灵敏度的区间模式阻尼提升策略。首先在采用SSI 算法从系统随机响应数据中提取系统振荡频率与阻尼比等参数的基础上,提出了全局灵敏度分析方法,进而设计了用于提高系统区间模式阻尼比的发电机有功定向提升策略,并将该方法分别应用于IEEE 2 区域4 机系统和IEEE 5 区域16机系统中,结果表明:
1)通过全局灵敏度分析方法计算得到的全局灵敏度指标能够准确辨识对系统区间模式阻尼比影响大的关键发电机有功功率参数;
2)根据全局灵敏度指标可以准确对参与调节的发电机组进行排序;
3)合理选取送受端发电机组并根据有功调制量改变发电机有功输出能够快速有效提升系统区间模式阻尼比,消除系统潜在威胁。
附录见本刊网络版(http://www.epae.cn)。
