基于侧输出融合卷积神经网络的电能质量扰动分类方法

王继东，张 迪

（天津大学 智能电网教育部重点实验室，天津 300072）

0 引言

传统的电能质量扰动分类分为扰动特征提取选择及分类器设计2 个阶段。目前，电能质量扰动特征提取算法有短时傅里叶变换、S 变换（ST）、小波变换及其改进方法等，对提取到的特征进行选择后作为分类器的输入对电能质量扰动信号进行分类。文献［1］采用改进ST 提取电能质量扰动信号特征，通过直接支持向量机SVM（Support Vector Machine）分类器进行分类识别；文献［2］采用离散小波变换DWT（Discrete Wavelet Transformation）提取特征，配合多层感知极限学习机进行电能质量扰动信号分类，但小波基的选取和品质因子Q的调谐存在困难等问题增加了算法的难度；文献［3］采用匹配追踪MP（Matching Pursuit）算法和粒子群优化PSO（Particle Swarm Optimization）算法相结合的分层搜索的原子分解法提取电能质量复合扰动参数。以上特征提取和分类器的组合算法在对电能质量扰动信号进行分类方面有着较好的表现，但这些算法主要凭借经验和统计量提取信号特征，特征的不足或冗余都会对后续分类器的精度产生较大的影响。文献［4-5］利用PSO 算法进行参数寻优来筛选出最优特征子集，但该方法对于不同类型和起止时刻的复合扰动类型的检测效果并不理想；文献［6］构造了一种基于欧氏距离的自适应度函数，利用改进的自适应遗传算法对原始特征进行筛选和组合优化，但该算法对于更多分类器的适用性有限。

扰动特征的选取是电能质量扰动信号分类的前提［7］，因此应采用一种更有效的方法自适应地对电能质量扰动信号进行特征提取和选择，排除人为因素的干扰。近年来，数据挖掘、深度学习方法的发展使得快速分类和处理大规模数据成为可能，因此将深度学习方法应用于电能质量扰动分类领域具有潜在优势［8-9］。文献［10］提出了基于Hoeffding Tree 算法的在线电能质量扰动分类方法，首先结合小波变换和离散傅里叶变换进行电能质量扰动检测，然后应用Hoeffding Tree 算法建立增量分类训练模型；文献［11］提出了一种基于稀疏自动编码器SAE（Sparse Auto-Encoder）深度神经网络的电能质量扰动算法，该算法利用稀疏自动编码器对电能质量扰动原始数据进行无监督特征学习，自动提取数据特征的稀疏特征表达。

本文提出了一种基于侧输出融合卷积神经网络SFCNN（Side-output Fusion Convolutional Neural Network）的电能质量扰动分类方法，能够自动对电能质量扰动信号进行特征选择及分类。针对一维序列的电能质量扰动信号，在卷积一层采用一维卷积，实现对电能信号序列的有效提取；通过对卷积神经网络CNN（Convolutional Neural Network）的低、中、高层信息进行特征融合，侧向输出融合分类结果，能够更好地把握信号的整体特征和局部特征，有效提高分类精度；通过批量归一化BN（Batch Normalization）结构和学习率设置优化CNN，避免过度拟合等问题；利用添加高斯白噪声的仿真数据对CNN 进行训练，提高网络的抗噪性。仿真和实测数据验证了本文方法的有效性。

1 CNN

CNN 是一种监督学习的网络模型，广泛应用于图像识别、语义分割、EGG 分类等领域，取得了令人瞩目的效果［12-13］。传统的CNN 包含卷积层、池化层、全连接层和Softmax 分类层［14］。在利用CNN 处理图像时，可以将其看作一个函数，函数的输入、输出分别为原始图像、分类的结果，即：

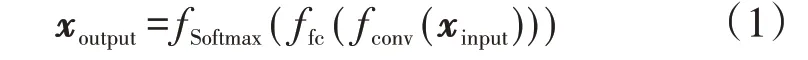
式中：xinput、xoutput分别为输入、输出；fconv(·)为卷积层运算；ffc(·)为全连接层运算；fSoftmax(·)为Softmax分类层运算。式（1）中包含可变的参数运算，CNN的训练过程即通过改变参数值，使网络获得良好的训练效果。为便于说明，下文对CNN 的各层进行说明时，均将该层作为第l层。

CNN组成说明如下。

1）卷积层。卷积层是CNN 自学特征提取的核心步骤，该层通过在数据上滑动卷积核，并与其覆盖的数据进行卷积操作提取特征。卷积层的运算为：

式中：fdown(·)为下采样函数，通常选取为最大池化函数（取局部感受视野内的各节点最大值）或平均池化函数（取局部感受视野内各节点平均值）；n为神经元个数。

3）全连接层（Dense层）：全连接层对卷积层和池化层提取到的特征进行综合，计算特征对应的类别，输出分类信息。全连接层的运算为：

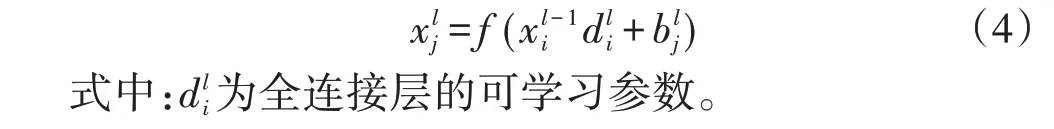
4）Softmax 分类层。Softmax 分类层是具有激活函数的全连接层，其用于建立特征与类别之间的完全连接，Softmax 分类层的输出值为输入样本属于相应类别的样本的概率，因此Softmax 分类层的神经元数量等于分类类别数量。第m个类别的Softmax 分类层的输出为：

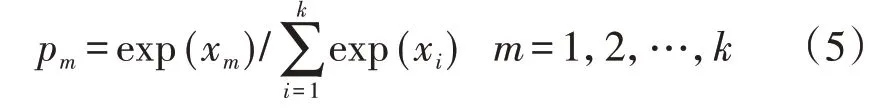
式中：k为样本类别数；pm为该样本被分为第m个类别的概率；xm为第m个类别的输出层待激活的神经元。

5）BN 层。BN 层一般位于卷积层或全连接层之后，通过规范化层输入数据解决数据内部协变量移位问题。BN层的主要原理公式为：

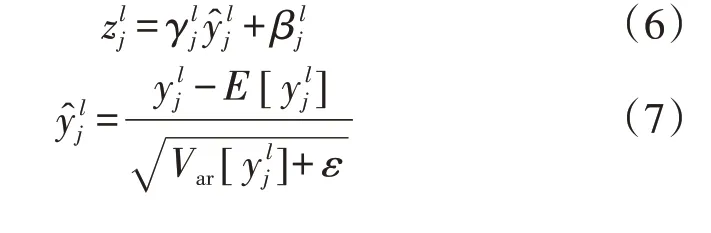
2 SFCNN分类模型

2.1 SFCNN的设计要求

在设计SFCNN 时，需要考虑电能质量扰动信号的2个因素。

1）电能质量扰动信号为一维信号，而CNN 广泛应用于二维图像的识别，文献［15］利用Wigner-Ville技术将一维电能质量扰动信号传输到二维图像文件中，然后利用CNN 进行识别，但这将增加计算量和操作复杂度，此外，将一维电能质量扰动信号转换至二维图像文件的过程中，可能会丢失重要信号细节特征。为使CNN 能够更好地识别一维电能质量扰动信号，需要对传统CNN的卷积层进行改进。

为了更好地对一维电能质量扰动信号进行分析处理，卷积层采用一维卷积滤波器。与传统二维卷积相比，一维卷积的计算量较少，只需要执行线性操作即可。则卷积层输出可表示为［16］：

2）电能质量扰动信号比较复杂，且复合扰动时有发生，训练后的CNN 应具有很强的泛化能力，可以精确识别各种类型的电能质量扰动，这就要求CNN 能够关注到扰动信号中的细节特征。此外，真实的电能质量扰动信号总是包含噪声，因此训练后的CNN应具有很好的抗噪性。

2.2 SFCNN结构

本文设计的SFCNN 结构如附录A 图A1 所示。SFCNN 结构包含S1—S3这3 个单元结构，每个单元结构将卷积层、BN 层、池化层组合在一起作为特征提取器；将S1—S3的卷积层的卷积滤波器数量分别设置为32、64、128 台，以逐层加深网络；将卷积步长设置为小步长1，使网络能够关注到电能质量扰动信号的细节特征，从而更加全面地提取特征；池化层用于提取电能质量扰动信号的显著特征，同时减少网络参数，由于最大池化方式的降噪效果要好于平均池化方式，因此池化层采用最大池化方式；在卷积层和池化层中间嵌入BN层对数据进行归一化处理，防止内部数据过度拟合，并提高网络的收敛速度；S1—S3的输出经过Flatten 层后分别展平为n维特征向量Ssideoutput1—Ssideoutput3，为了更好地比较融合层输出与卷积低、中、高层输出，搭建网络模型时，使用函数式应用程序接口（API）构建多输出模型，在S1—S3的Flatten 层后添加全连接层，最后由Softmax 分类层得到各单元结构的分类准确率。

通过对ResNets、GoogleNet 等先进的经典CNN模型进行分析可知，在网络传递过程中，网络低层更加关注细节特征，提取到的低层特征伴随着网络的深入进行传递，逐步提取到高层特征，在该过程中，低层特征难免会丢失。因此本文利用融合层对不同卷积层的输出进行融合，融合层结构如图1 所示。融合层的输入为特征向量Ssideoutput1—Ssideoutput3，融合层将这3 个特征向量首尾相连，拼接为1 个特征向量，从而实现特征融合。融合信号包含电能质量扰动信号的各级特征，且各级特征之间可以互补，低层特征可协助SFCNN提取适当的高层特征，提高SFCNN识别电能质量扰动的能力。

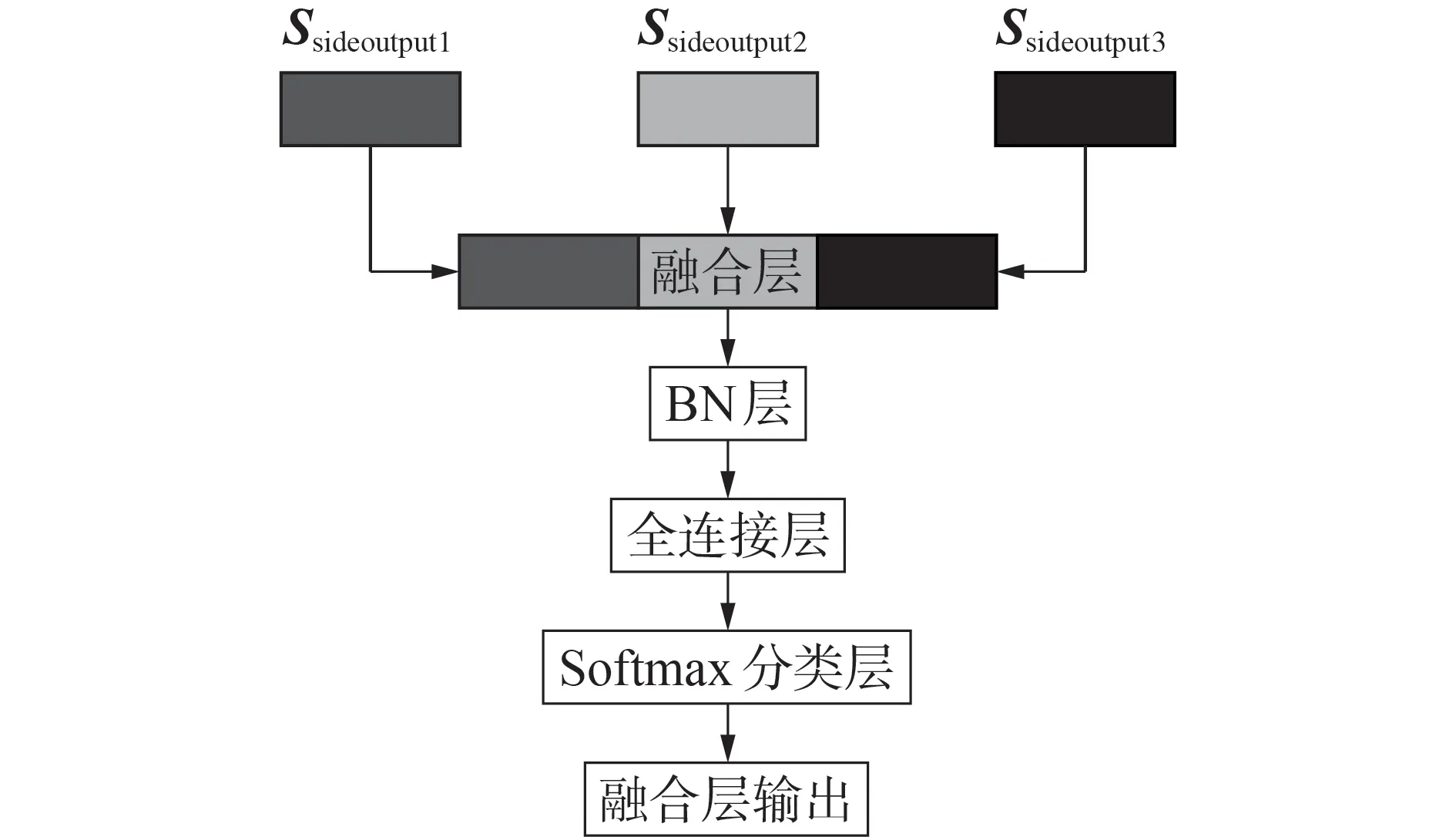
图1 融合层结构Fig.1 Structure of fusion layer

3 仿真分析与结果验证

3.1 实验准备及数据获取

采用包括纯正弦波在内的15 种电能质量扰动信号来评估所本文所提基于SFCNN 的电能质量扰动分类方法的性能。电能质量扰动信号由10 种单一类型和5 种复合类型的信号组成，前者包括纯正弦波形（C1）、暂降（C2）、暂升（C3）、中断（C4）、谐波（C5）、脉冲瞬态（C6）、振荡瞬态（C7）、闪变（C8）、电压切痕（C9）和尖峰（C10）信号，后者包括谐波暂降（C11）、谐波暂升（C12）、谐波中断（C13）、暂降闪变（C14）和暂升闪变（C15）信号。图2为典型电能质量扰动仿真信号波形图，图中幅值为标幺值，后同。参数变化符合IEEE Std 1159—2019标准中的参数方程［17］。

图2 仿真信号波形图Fig.2 Waveforms of simulative signals

仿真信号在MATLAB 环境下产生，采样频率设置为6.4 kHz，单个样本数据长度为1 280，通过随机更改约束参数，可以生成无限数量的数据。因此，仿真信号可以满足深度学习对训练数据数量的要求。每类电能质量扰动信号有500 个样本，共产生4 500个训练集、1 500 个测试集。为了便于计算损失函数，利用one-hot 编码表示标签数据，例如［1，0，0，0，0，0，0，0，0，0，0，0，0，0，0］表示样本属于第1 个类别。

实际的电能质量扰动信号采集过程不可避免地会受到采集设备以及环境噪声的干扰，为了提高SFCNN 的泛化性，在采样信号中叠加信噪比为50、40、30、20 dB的噪声作为干扰以模拟真实信号，使用不同水平的模拟噪声来训练SFCNN。表1为本文所采用的数据集。

表1 训练样本数据集Table 1 Training sample dataset

3.2 仿真数据验证

基于Keras 框架训练SFCNN，实验训练阶段设置小批次数据量为128，训练迭代轮次为50，通过训练集和测试集中的交叉熵损失LCE和分类准确率rc来评价SFCNN 的性能。网络模型精度越高，交叉熵损失越小，说明网络模型性能越好。训练集和验证集的分类准确率与交叉熵损失对比如图3 所示。由图可见，采用随机小批量方式进行50 次迭代训练期间，在20 次迭代之后训练集和验证集的分类准确率几乎相等，最高分类准确率在99.5%以上。

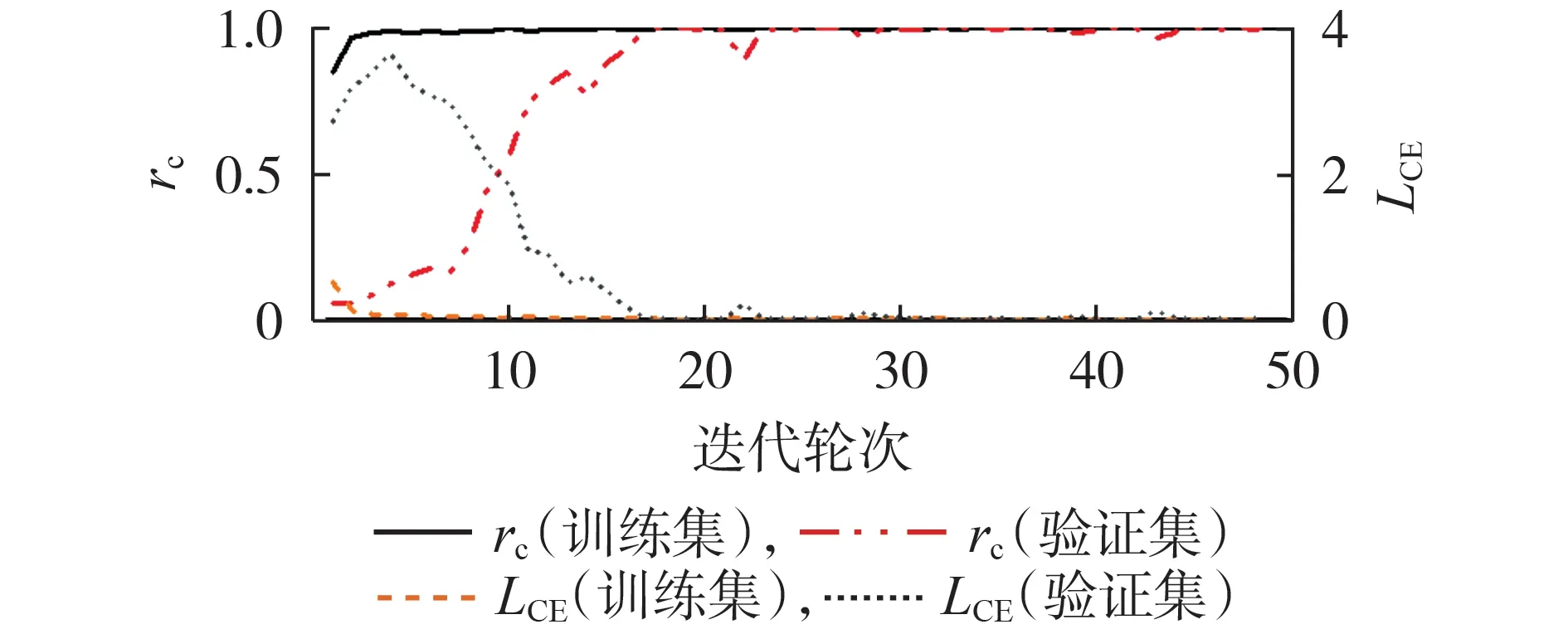
图3 训练集和验证集的分类准确率与交叉熵损失的对比Fig.3 Comparison of classification accuracy rates and cross entropy losses between training set and verification set

为进一步验证融合层的性能，将融合层的分类准确率与卷积低、中、高层的分类准确率进行对比，结果见图4。由图可见：迭代轮次较少时，融合层的分类准确率明显高于卷积低、中、高层的分类准确率；随着迭代轮次的增加，卷积中、高层的分类准确率明显增加，但融合层的分类准确率始终高于卷积高层的分类准确率，可见进行特征融合后分类效果较好。

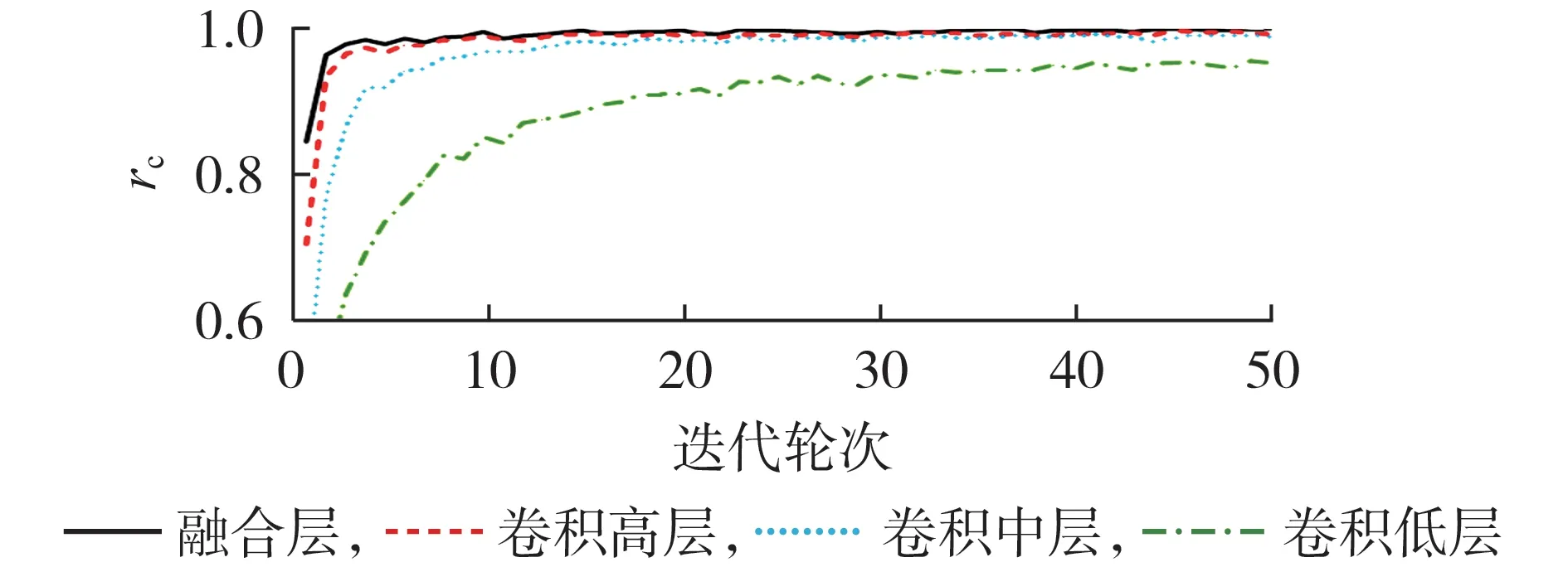
图4 融合层与各卷积层的分类准确率比较Fig.4 Comparison of classification accuracy rates between fusion layer and convolutional layers

3.3 SFCNN性能优化设计

为确定学习率α对SFCNN 性能的影响，在不同学习率下对SFCNN进行训练优化，结果如图5所示。由图可见，学习率较低时网络收敛速度较慢，学习率过高又会导致网络学习性能不稳定，综合来看，学习率为0.001 时SFCNN 的性能最好，因此本文设置学习率为0.001。

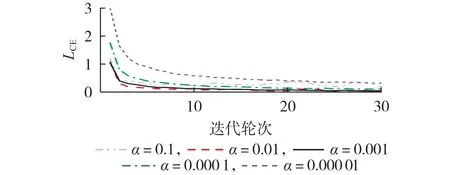
图5 不同学习率下的交叉熵损失对比Fig.5 Comparison of cross entropy losses among different learning rates

为验证BN 层对于SFCNN 性能的影响，对比包含和不包含BN 层的SFCNN 的分类准确率和交叉熵损失，结果如图6 所示。由图可以看出，包含BN 层的SFCNN 的分类准确率要高于无BN 层的SFCNN，其交叉熵损失更小，收敛速度更快，可见BN 层可以优化网络模型结构，防止网络的过拟合。

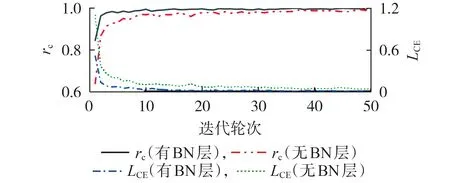
图6 有、无BN层情况下的分类准确率与交叉熵损失的对比Fig.6 Comparison of classification accuracy rates and cross entropy losses between with and without BN layer

3.4 特征可视化分析

为了更加直观地理解SFCNN 对于电能质量扰动信号的特征提取过程，采用t 分布随机近邻嵌入（t-SNE）技术［18］，对输入数据及融合层输出进行可视化。设置t-SNE的迭代轮次为1000、困惑度为30，对输入数据以及融合层输出特征的可视化结果见附录A 图A2和图A3。由图A2可见，输入数据分布杂乱，彼此重叠交叉；由图A3 可见，经过SFCNN 处理后，同类别的数据聚合在一起，不同类别的数据之间距离变大，没有重叠现象，正常信号和不同类别的电能示例扰动信号在二维平面上均能明显区分，说明了特征融合的有效性。

3.5 SFCNN与现有方法的比较

为了验证本文方法的优越性，将本文算法与3种先进的深度学习算法进行对比，对比算法简要介绍如下。

1）深度CNN（DCNN）：选取文献［19］提出的具有6 个标准卷积层的DCNN，卷积核大小设置为3，步长设置为1，各卷积层过滤器的数量设置为32、32、64、64、128、128，全连接层数为3。

2）长短期记忆网络（LSTM）：采用3 层堆叠式LSTM 结构，各层的LSTM 记忆节点数分别为32、32、32，激活函数为tanh。

3）CNN-LSTM：文献［20］设计了具有2层标准卷积层的CNN，卷积核大小设置为3，卷积层过滤器数量为64和128，将其与LSTM结合进行电能质量扰动信号分类，LSTM层数为1，LSTM记忆节点数为50。

设置迭代轮次为50 次，在相同配置的计算机和数据集上对4 种算法进行训练，训练时间为算法迭代一次所用时间，性能对比结果如表2 所示。表中，RSN为信噪比。由表可见：LSTM 的训练时间最短，但在各种信噪比下的分类准确率均低于其他方法；综合考虑训练时间和分类准确率，本文所提的SFCNN取得了较好的效果，优于其他3种深度学习算法。

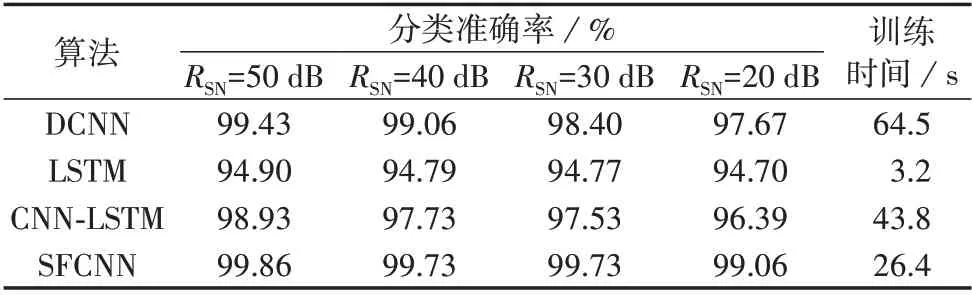
表2 4种深度学习算法的性能比较Table 2 Performance comparison among four deep learning algorithms

将SFCNN 与文献［2］采用的DWT 和分层极限学习机（H-ELM）方法（DWT+H-ELM），文献［21］采用的ST 和概率神经网络（PNN）方法（ST+PNN）、文献［22］采用的可调品质因子小波变换（TQWT）和随机森林（RF）方法（TQWT+RF）进行对比，结果如表3所示。表中，“—”表示文献［21］中未直接给出分类准确率。传统的电能质量扰动分类方法中，对信号分解后要对特征进行选择，关于特征数量的选取并没有明确的规定，文献［21］仅选取了4个特征，在30 dB的信噪比下，分类准确率为98.63%，而文献［22］选取了16 个特征进行分析，在相同的噪声条件下，分类准确率达到了98.13%，两者准确率接近，说明特征的类型及数量差异导致了分类结果的差别。本文所提基于SFCNN 的多层信息融合结构可以自动提取有效特征，不仅简化了电能质量扰动识别的过程，而且缩短了特征的提取和选择时间，训练后在各种噪声条件下的分类准确率均高于其他传统方法。

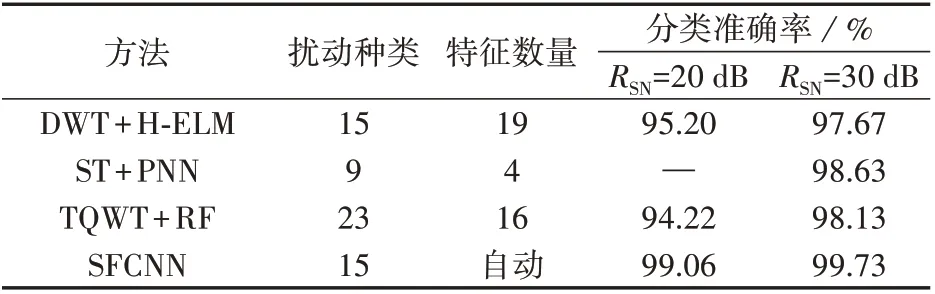
表3 SFCNN和传统方法的分类准确率对比Table 3 Comparison of classification accuracy rates between SFCNN and traditional methods

3.6 实测数据验证

为了验证本文方法对实测信号的适用性，采用一组实测信号来测试SFCNN 的分类性能。实际信号来自IEEE PES 数据库提供的用于电能质量扰动分类的数据，每个信号的长度为1 536，信号采样率为每周期256个点。

由于网络模型需要大量数据进行训练优化，数据的优劣直接决定所训练模型的适应性和可行性。针对个别类别的数据量少、数据分配不均衡的问题，采用数据增强的方法，通过随机裁剪、添加高斯噪声、随机翻转操作进行数据增强，增加训练数据量。以实测暂态振荡信号为例，进行数据增强后的结果见图7。

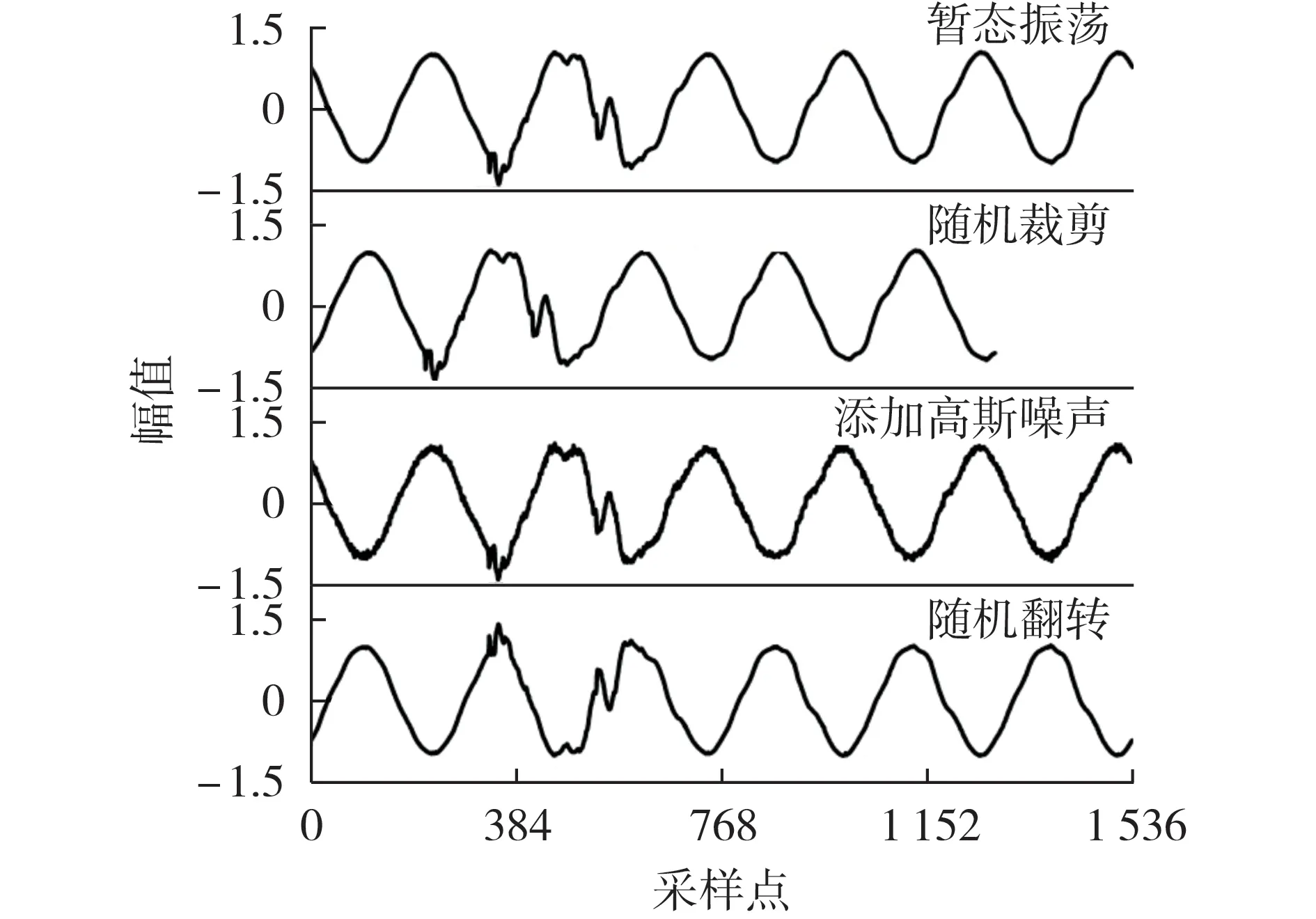
图7 数据增强结果示例Fig.7 Example of data enhancement results

对数据集进行增强后，训练集、测试集的样本数量分别为3 000、500。使用增强后的数据集训练本文所提SFCNN和3.5节中的DCNN、LSTM、CNNLSTM，得到的电能质量扰动分类结果如表4 所示。可以看出，SFCNN 对增强后的实测数据的平均分类准确率为97.2%，低于仿真结果，其主要原因是训练数据是使用仿真软件生成的，与真实数据有一定的差别，而真实数据的信号所受干扰更加复杂，且实测数据量较小，类别之间分布不均匀，以及人工标注存在误差等，容易造成网络训练准确率有所下降。

表4 数据增强后的实测信号分类结果Table 4 Measured signal classification results after data enhancement

4 结论

本文针对传统电能质量信号扰动识别存在的人工选取特征困难、计算量较大等缺陷，提出了一种基于深度学习的SFCNN 进行电能质量扰动信号分类，主要工作及结论如下。

1）构造了一种新型的侧输出融合结构，该结构可整合不同卷积层的信息，自动提取特征，实现电能质量扰动信号分类。

2）采用一维卷积处理电能质量扰动信号，将BN层引入SFCNN，以加快网络收敛速度，防止过拟合。

3）本文所提的SFCNN 可以将传统电能质量扰动检测和识别系统的扰动特征提取选择和分类2 个主要模块融合到一个学习体中，提高了分类准确率，节省了人力并简化电能质量扰动信号分类流程；仿真和实测数据验证了本文所提的SFCNN 可以有效地学习分类电能质量扰动信号，分类准确率较高，且抗噪性能较好；SFCNN 的输入数据以及融合层输出特征的t-SNE 可视化结果也从侧面说明了SFCNN 的有效性。

附录见本刊网络版（http：//www.epae.cn）。