考虑用户需求的电动汽车虚拟同步机辅助调频控制策略

2021-11-20李家浩李泽宁王业庭王世丹

电力自动化设备 2021年11期

苏粟，李家浩，李泽宁，王业庭，夏冬，王世丹

（1. 北京交通大学国家能源主动配电网技术研发中心，北京 100044；2. 国网新源控股有限公司，北京 100761；3. 国网天津市电力公司经济技术研究院，天津 276000；4. 国网北京市电力公司海淀供电公司，北京 100000）

0 引言

随着能源危机的加剧，作为新能源汽车代表的电动汽车EV（Electric Vehicle），已被公认为21 世纪汽车工业发展的主要方向，为此世界各国高度重视EV 的开发和推广［1］。我国“十二五”期间规划加大对EV 等新能源领域的投入和支持力度，为国内EV市场的启动和加速发展提供了强大的动力［2］。EV的快速发展将对电网产生巨大的影响，从而促进了车网互动V2G（Vehicle-to-Grid）技术的研究［3］。EV不仅可以作为负荷，也可以作为分布式储能为电网提供辅助服务［4］。其中，EV 向电网提供的辅助调频服务被认为是V2G 最有价值和前景的研究方向［5］，并已逐渐成为研究热点之一［6］。

由于传统的V2G技术“只管自身放电，不顾及电网”，当大量EV 入网后会造成电网惯量以及阻尼缺失的问题。虚拟同步机VSM（Virtual Synchronous Machine）技术作为解决这一问题的有效手段受到了国内外学者的广泛关注［7］。VSM 有虚拟同步整流器VSR（Virtual Synchronous Rectifier）与虚拟同步发电机VSG（Virtual Synchronous Generator）2 种工作模式，其主要工作原理为模拟同步机组的电磁、阻尼特性，使变流器的运行特性更接近于同步机［8］。将虚拟同步发电技术应用于V2G 参与调频的过程中，可以有效解决大量EV入网时造成的惯量、阻尼缺失问题，提高电力系统的稳定性。

目前，关于EV 参与调频的研究主要包括2 个方面：①对EV 与可再生能源进行协同配合调频，如文献［9］提出一种时滞环境下应用EV和电热泵协同参与系统负荷频率控制的调控策略；文献［10］研究了EV 接入高风电渗透率的丹麦电网参与调频的方法；②对EV自主参与频率调整的方法进行研究，如文献［11］提出了EV 参与一次调频的自适应下垂控制模型，并详细仿真了EV 参与一次调频对电网的影响；文献［12］提出了一种计及EV 辅助调频的负荷频率控制联合优化方法，有效地改善了负荷频率控制的稳态响应速度，优化了系统的调频性能；文献［13］针对家用EV用户的差异性，在出行链理论的基础上提出了一种计及停车时长充裕度以及分时电价的充电需求分布分析方法，但是没有考虑EV参与调频辅助服务；文献［14］基于VSM 提出了一种电网友好的EV 快充解决方案，可以在减小对电网影响的同时对EV 进行快速充放电；文献［15］设计了基于VSM 的辅助调频控制算法，通过计算“功率参考值修正量”改变EV 的充放电功率参考值，使得EV 参与微电网的一次、二次调频；文献［16］将VSM 技术应用于V2G 中，并基于电池的荷电状态SOC（State Of Charge）以及电网频率波动，设计了模糊控制器用于解决VSM 的智能充放电问题，但并未考虑用户充电需求；文献［17］提出了根据已入网时长内EV的平均充电功率Pav反映用户充电需求的方法，但EV 入网剩余时间的平均充电功率可能偏离Pav，那么以Pav反映用户的充电需求就有可能出现偏差，且并未研究EV向电网放电的情况；文献［18］设置了一个可参与调频的SOC 阈值，当EV 的SOC 达到该阈值时，则可以通过V2G 参与电网调频，但这种控制方式并不能反映用户的需求程度与调频功率之间的关系。

合理的EV 调频策略需要兼顾电网与用户二者的需求，为此本文采用电网友好型的VSM 技术来控制EV 参与调频，并在文献［17］的基础上进行改进，提出一种更合理的反映用户需求程度的参数，设计T-S模糊控制器控制EV通过充放电参与调频辅助服务，可以在充电时间结束时达到用户期望SOC。首先，基于VSG 技术建立了EV 充放电模型；然后，将所提参数应用到EV 的一、二次调频过程中，并设计了输出精度更高的T-S 型模糊控制器来参与二次调频，由于输出为输入的线性函数，T-S 型模糊控制器可以根据调频参与度因子的大小更精确地控制EV充放电；最后，通过仿真对比验证了所提控制策略的有效性和优越性。

1 EV充放电模型架构

1.1 基于VSG的EV模型

本文研究的EV 充放电模型如图1 所示，其由VSG 模块、双向DC／DC 变流器模块、调频参与度因子计算模块、一次调频模块以及二次调频模块构成。其中，VSG 模块具有变流、补偿阻尼的功能；双向DC／DC 变流器模块用于稳定直流母线电压；调频参与度因子计算模块综合用户期望充电时间Tpl、期望SOCSSOC，e以及当前SOCSSOC，1计算得到反映用户充电需求程度的调频参与度因子α，将其与电网频率偏差Δf输入一、二次调频模块，分别得到一次调频功率P1和二次调频功率P2，最终相加得到VSG 的有功参考功率Pset，用于控制EV智能充放电。

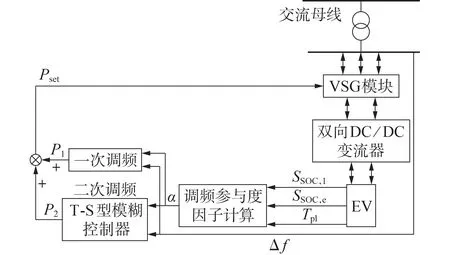
图1 EV充放电模型Fig.1 Charging and discharging model of EV

1.2 VSG的电路及控制结构

VSG 的电路拓扑结构如图2 所示。EV 动力电池通过前级双向DC／DC 变流器与后级DC／AC 变换器进行充放电。其中，双向DC／DC 变流器采用电压电流双环控制来稳定直流侧电压；DC／AC 变换器采用VSG 控制策略，根据辅助调频模块输出的功率控制EV 进行智能充放电。图2 中，Vn为直流侧电压；Vga、Vgb、Vgc为电网侧三相电压；ea、eb、ec为VSG输出电压；ia、ib、ic为VSG 输出电流；Rg、Lg分别为电网侧电阻、电感；Rs、C、Ls分别为直流侧电阻、电容、电感，这三者共同构成滤波器，用于滤除变流器输出的谐波电流；Va、Vb、Vc为电容电压降；U*dc为直流母线参考电压，即双向DC／DC 变流器的电压外环参考信号；ω为VSG转子的实际角频率；f为电网频率。

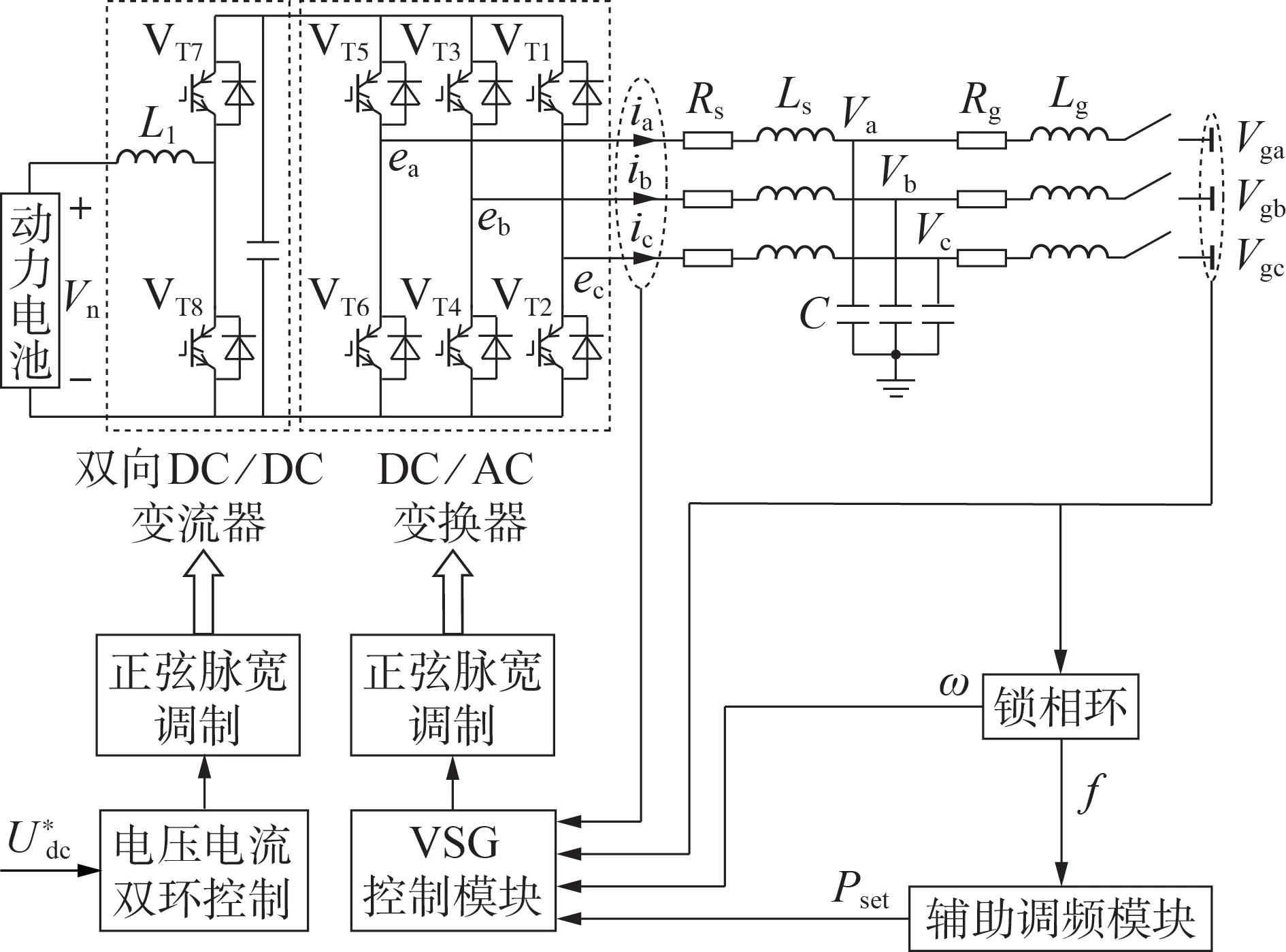
图2 VSG的电路拓扑结构Fig.2 Topological structure of VSG circuit

目前，关于VSG 的建模已有诸多研究，且对于机电部分的建模较为统一。本文采用文献［7］中可同时反映VSG 的机电与电磁暂态特性的同步机模型，可增强虚拟定子与转子之间的联系，更接近VSG的特性。VSG的运动方程可表示为：

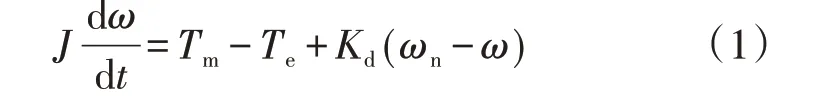
式中：Te、Tm分别为电机的电磁转矩、机械转矩；J为VSG 的转动惯量；Kd为转子的阻尼系数；ωn为转子的参考角频率。

电磁转矩Te的计算式为：

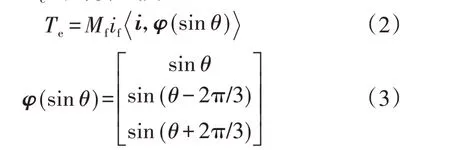
式中：Mf为电机定子与转子之间的互感；if为定子的励磁电流；i为VSG 输出的三相电流向量；θ为转子磁场与a 相定子绕组之间的角度；⋅，⋅表示向量的点乘运算。

VSG 输出电压e和VSG 输出的无功功率Q分别为：

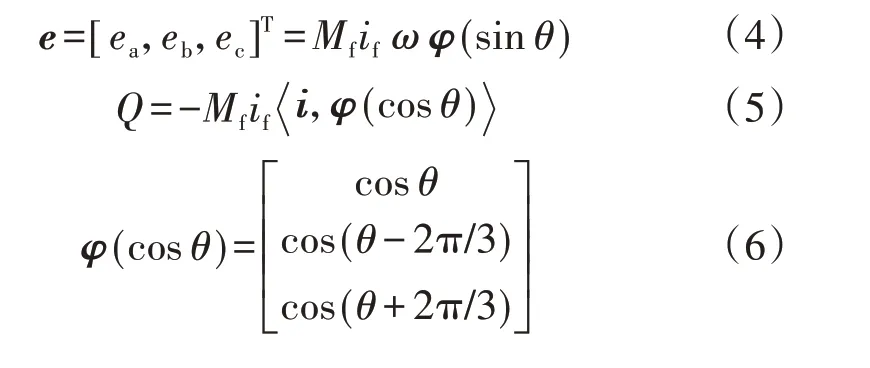
在图2 所示结构图中，将滤波器的Ls、Rs分别等效为VSG 定子绕组的电感、电阻，将VSG 输出电压ea、eb、ec等效为电机电动势，将电容电压降Va、Vb、Vc等效为发电机定子电压，将VSG 输出电流ia、ib、ic等效为定子电流，则可以将图2 所示电路的交流侧在数学上等效为1 台VSG，这样EV 入网时就具备发电机的惯性、阻尼特性以及电压／频率下垂特性，其控制结构如图3 所示。图中，Qset为设定的无功参考功率，一般设置为0；Dp为频率环的下垂系数；Dq为电压环的下垂系数；Vm、Vr分别为电网电压有效值及其参考值；K为积分系数。

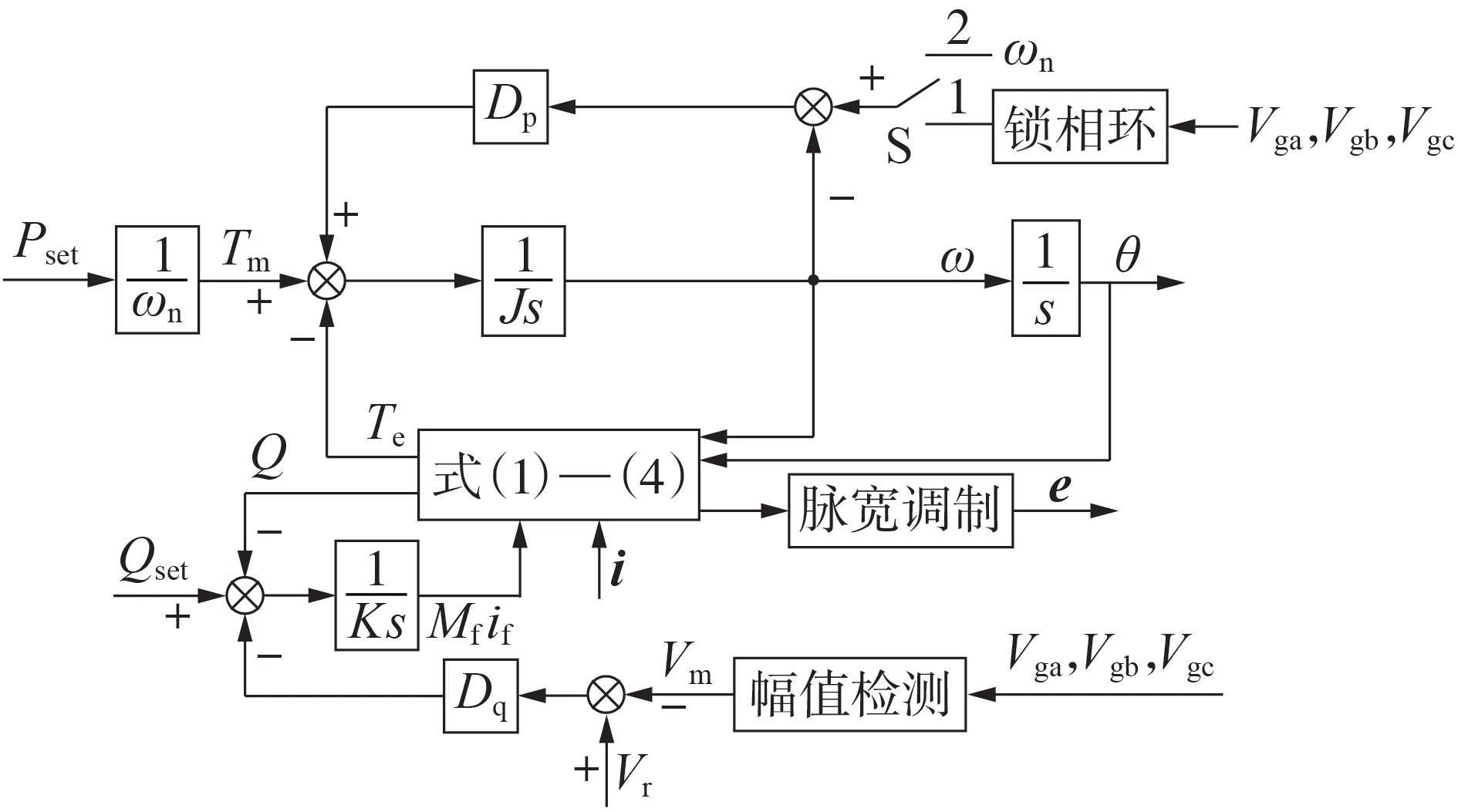
图3 VSG的控制结构Fig.3 Control structure of VSG

根据开关S 位置的不同，VSG 有2 种工作模式：①当开关S 位于2 时，VSG 工作在下垂控制模式，具有频率／电压下垂特性；②当开关S 位于1 时，VSG工作在PQ控制模式，输出给定的有功参考值。在本文研究中，使VSG 的有功／频率环工作在下垂控制模式，可根据电网频率波动实现一次调频。无功／电压环同样工作在下垂控制模式，可实现无功／电压的调节。

2 EV辅助调频控制策略

2.1 调频参与度因子α

EV 参与电网辅助调频时需要考虑用户的充电需求。而反映用户充电需求的参数主要有用户期望充电时间Tpl和在规定时间内期望达到的SOC 值2个。本文设计了一种更加合理的、可以反映用户充电需求的参数——调频参与度因子α，设计原则如下：检测并计算EV在剩余入网时间内能否以额定功率充电达到用户的期望SOC，如果以额定功率充电达到期望SOC 的时间小于剩余入网时间，则表示可以满足用户的充电需求，EV处于可以参与V2G调频的“可控状态”；如果以额定功率充电达到期望SOC的时间大于或等于剩余入网时间，则表明不能满足用户的充电需求，EV 处于只能单向充电的“充电状态”。这样就可以在入网时间等于用户设定的时间时，保证达到期望SOC。定义反映用户需求程度的调频参与度因子α的计算式为：

本文设置α的临界值为0，若α<0，则表明EV在剩余入网时间内不足以充电至期望SOC，此时EV 工作在额定功率充电模式，不参与电网调频；若α=0，即Tpl=t1+t2，则EV 停止参与电网调频，并以额定功率充电，这样能保证EV在剩余入网时间内刚好充电至期望SOC，以满足用户的充电需求；若α>0，则表明EV 的剩余入网时间充足，可以参与电网调频，且α越大，调频能力越强。用户可根据自身的计划充电时间与SSOC，e设置α的取值，当用户设定的α<0时，表示用户不希望EV 参与调频，EV 工作在额定功率充电模式下。而对于可参与调频的EV而言，考虑到充电桩的占用问题以及实际的充电情况，本文将α的取值限制在［0，1］范围内，这样当α取值趋近于0时，可以控制EV 的充放电功率随α取值的减小衰减至0，从而避免过充与过放。

2.2 EV参与一次调频的控制策略

采用下垂控制实现EV参与一次调频，规定功率流动的正方向为由电池流向交流侧电网，且为了减少电池的充放电次数，防止EV 频繁充放电，设置了一次频率死区fdeath。EV 参与一次调频的下垂特性曲线见附录A 图A1。设电网的额定频率为fn，当电网频率偏差Δf=f-fn处于［-0.05，0.05］Hz 范围内时，EV不动作。

在传统的一次调频过程中，功率的变化仅由频率决定且与频率呈负线性关系，忽略了EV固有的交通属性，容易造成EV 过充和过放，偏离用户的充电计划。本文进一步考虑EV的移动储能特性，即考虑用户的充电需求特性，当α取值较小时，EV 应多充电少放电；当α取值接近1 时，EV 应多放电少充电。本文基于调频参与度因子α，设最大下垂系数为Kmax，那么设置放电时的下垂系数为αKmax，充电时的下垂系数为(1-α)Kmax，这样就可以根据α的取值大小自适应调整下垂系数。自适应下垂系数的变化曲线如图4所示。

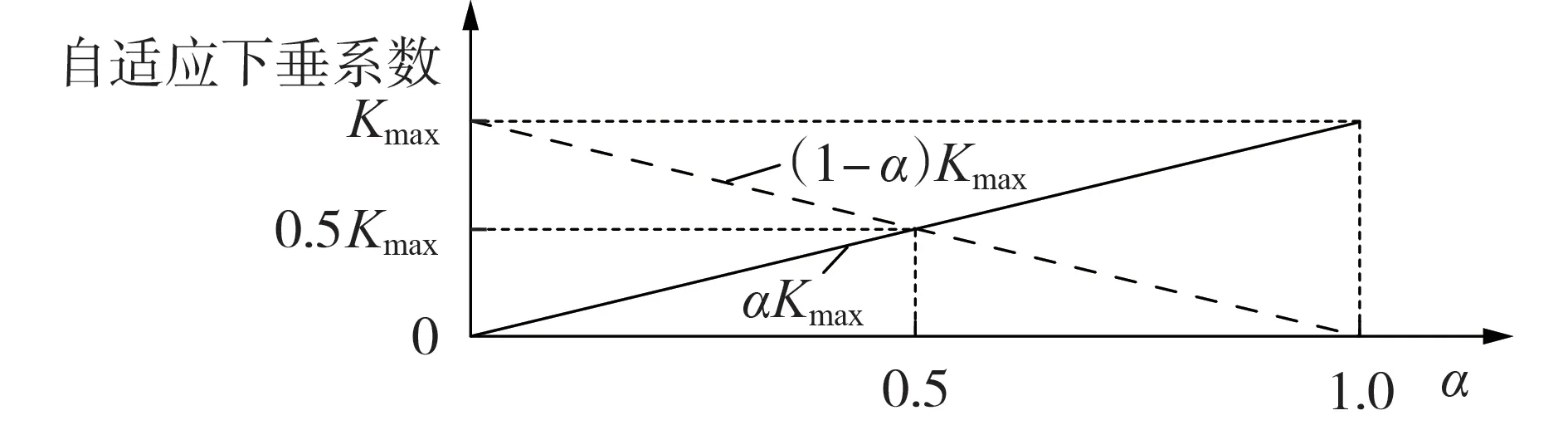
图4 自适应下垂系数的变化曲线Fig.4 Change curve of adaptive droop coefficient

则EV参与一次调频的功率P1可以表示为：

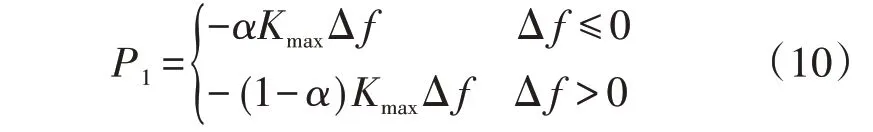
当α>0时，EV参与电网调频。若电网频率不高于额定频率，EV 将向电网输出功率，此时α会缓慢降低并逐渐趋近于0，则放电功率会随着α的减小衰减到0，避免了过放；若电网频率高于额定频率，EV将从电网吸收剩余功率，此时α会缓慢增加并逐渐趋近于1，则充电功率会逐渐减小为0，避免了过充。当α<0 时，EV 不参与电网调频，工作在额定功率充电模式。

EV 参与一次调频的控制策略框图见附录A 图A2。为了防止EV 在Δf=0.05 Hz 处频繁充放电，加入了滞环控制，用于提高系统稳定性。功率限制模块用于限制EV的最大充放电功率。

2.3 EV参与二次调频的控制策略

当电网频率波动过大且仅靠一次调频作用不能使频率偏差保持在允许范围内时，就需要增大或减小EV的充放电功率以参与电网的二次调频，本文设置二次调频的动作阈值为|Δf|≥0.1Hz。

EV 参与二次调频的充放电功率与用户的充电需求、电网频率之间存在复杂的非线性关系，无法用固定的数学模型进行描述。而模糊控制可以将人为经验转化为相应的控制策略，对难以建立模型的系统实现有效的控制。文献［17］设计了Mamdani型模糊控制器，用于控制EV 充放电，但Mamdani 型模糊控制器的输出结果不连续，且存在模糊误差。本文采用控制精度更高的T-S 型模糊控制器，其输出为输入变量的线性函数，无需再进行去模糊化，大幅提高了控制精度，且可由模糊控制器的输出直接得到EV的充放电功率，无需设计参考功率。

本文所采用的T-S 型模糊控制器的一个输入量为Δf，用于反映电网的频率波动；另一个输入量为α，用于反映用户的充电需求。由于T-S 型模糊控制器的输出为输入函数的线性函数，当α取值接近于0时可以控制放电功率减小至0，保证电池不会过放，在满足用户需求的前提下，参与电网的辅助调频服务。

输入量Δf与α均采用运算简单且效率高的三角形隶属度函数μ(x)来定义模糊变量的语言值［16］。

1）电网频率偏差Δf的模糊化。

考虑到3 000 MW 以下系统允许的电网频率偏差范围为±0.5 Hz，本文将电网频率偏差的模糊语言变量Δf͂论域定义在闭区间［-0.5，0.5］内，量化因子取值为1，其论域内有5个模糊语言变量｛NB，NS，Z，PB，PS｝，分别表示电网频率偏离额定频率的程度为负大、负小、零、正小、正大。Δf的隶属度函数见附录A图A3。

2）调频参与度因子α的模糊化。

将调频参与度因子的模糊语言变量ᾶ论域定义在区间［0，1］内，量化因子取值为1，其论域内有5个模糊语言变量｛Z，S，M，L，VL｝，分别表示α偏离1 的程度为零、小、中等、大、极大。α的隶属度函数见附录A图A4。

本文所采用的模糊控制规则如式（11）所示。

模糊控制规则的设计依据如下：EV 的二次调频功率由电网频率偏差Δf与调频参与度因子α共同决定。当系统负荷增多导致Δf<0 时，若用户的充电需求小，即α取值接近于1，控制EV 向电网放电，且α取值越大，放电功率越大；若α取值接近于0，虽然此时电网频率低于额定值，但由于用户的充电需求很高，因此设置EV工作在不放电或者以小功率充电的模式，设计二次调频功率Pi2主要由biα决定，这样可以控制EV 放电功率随α取值的减小而减小至0；而当系统负荷减少导致Δf>0 时，EV 全部工作在充电模式，用户的充电需求越高，则EV 充电功率越大，因此设计充电功率随着α取值的减小而增大，此时设计二次调频功率Pi2主要由c决定，c会随着不同的情况变化，这样可实现充放电功率的精细控制。

根据上述分析，设计充放电模糊控制规则如表1 所示。表中，Ki=1000i（i=1，2，…，6），单位为W，正值表示放电，负值表示充电。

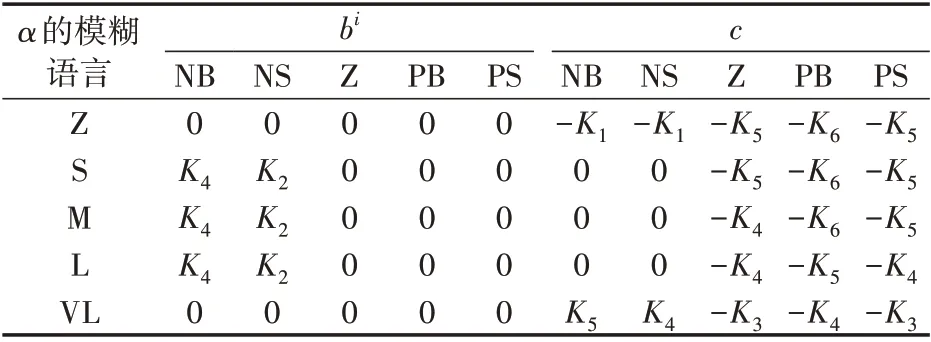
表1 充放电模糊控制规则Table 1 Fuzzy control rules for charging and discharging power

EV 参与二次调频的控制框图见附录A 图A5。监测器实时采集EV 的当前SOC，并综合用户设置的期望SOC、期望充电时长Tpl计算调频参与度因子α，模糊控制模块根据计算所得α的值以及当前电网频率偏差输出二次调频功率，最后采用功率限制模块设置的功率限值Plimit对输出功率进行限制。

3 仿真分析

本文选取某单区域系统为例进行仿真分析，其额定发电功率为300 MW，额定频率为50 Hz，EV 动力电池采用应用广泛的磷酸铁锂电池，额定充放电功率为8 kW。在MATLAB R2017a／Simulink 环境下搭建仿真模型，并对所提控制策略进行仿真验证。为了实现对模型进行较长时间的仿真研究，逆变器采用平均值等效模型，允许使用较大的仿真步长。VSG仿真参数见附录B表B1。

3.1 转动惯量和阻尼系数验证

VSG 技术在EV 参与调频时可以为电网提供惯性和阻尼支持，对此进行仿真验证：EV 在初始时刻以3 kW 功率放电，在t=4 s时放电功率变为8 kW，不同转动惯量J和阻尼系数Kd下VSG 的响应功率曲线见附录B 图B1。由图B1（a）可以看出：当J=0.1 kg·m2时，VSG响应功率的变化速度最快，响应时间约为0.05 s，且超调量为0；而当J=0.25 kg·m2时，VSG响应功率的变化速度变缓，响应时间约为0.1 s，且出现超调量；当J=0.5 kg·m2时，VSG响应功率的变化速度最慢，响应时间约为0.3 s，且超调量最大。可见，转动惯量J可以延缓功率的响应速度，从而降低频率的变化速度。由图B1（b）可以看出：当Kd=6时，VSG 响应功率的振荡幅值最大，且动态响应时间最长，呈现欠阻尼状态；当Kd=12 时，响应功率的振荡幅值变小且响应时间缩短；而当Kd=18 时，VSG 可以由变化之前的稳定值平滑地过渡到新的稳定值，且响应时间缩短，呈现过阻尼状态。可见，阻尼系数Kd可以抑制功率响应的振荡，且Kd值越大，动态响应功率振荡幅值的衰减速度越快。

3.2 充放电控制策略的有效性验证

本节对所提EV 参与调频的控制策略进行仿真验证。首先，根据用户的充电需求即α的取值对EV进行分类，设计4 辆不同状态的EV 代表4 种不同类型的用户：EV1—EV4分别代表充电需求低、中等、大、极大的用户。然后，考虑电网频率接近额定频率、电网频率偏高、电网频率偏低这3 种电网运行工况。最后，为了测试EV 充放电控制策略，设置如下时序进行仿真测试：［0，2］s 电网频率为50 Hz（运行工况1），（2，8］s 频率发生幅值为0.3 Hz 的正弦波动（运行工况2），（8，14］s 频率发生幅值为-0.3 Hz 的正弦波动（运行工况3）。EV 的仿真参数见附录B 表B2。仿真结果见附录B图B2。

1）运行工况1。

由图B2 可以看出，［0，2］s 内电网频率等于额定频率，负荷需求与发电机出力平衡，一、二次调频模块均不动作，由于EV4的α<0，其在任何情况下都以额定功率充电，SOC 匀速上升，而EV1—EV3的充放电功率为0，SOC 保持不变。此外，除了EV4的α有所上升外，EV1—EV3的α都有不同幅度的下降，这是因为虽然EV1—EV3的充放电功率为0，但其入网时间越来越短，从而导致α呈逐渐减小的趋势。

2）运行工况2。

（2，8］s 内，电网中的有功功率过剩，电网频率高于额定频率，一、二次调频模块在满足动作阈值时动作，EV1—EV4均工作在充电模式，SOC有不同程度的升高。其中，EV1的α最大，表明其入网时间可以充分满足用户的需求，因此其充电功率最小；EV2的α接近于0.5，同样呈减小的趋势，表明用户的充电需求程度为中等，且其充电功率大于EV1；EV3的α接近于0 并不再减小，表明在其入网时间内以额定功率充电刚好能充至用户的期望SOC，因此其充电功率接近额定充电功率；EV4的α<0，故其以额定功率充电。

3）运行工况3。

（8，14］s 内，电网处于负荷高峰时段，电网频率低于额定频率，一、二次调频模块在满足动作阈值时动作。此时，α值越大的EV，其放电功率越大。其中，EV1当前的α值最大，因此其放电功率最大，SOC下降最快；EV2的α值小于EV1的α值，故其放电功率也小于EV1的放电功率，SOC 下降速率小于EV1；EV3的α值接近于0，因此其工作在小功率放电或者不放电模式，SOC 几乎保持不变；而EV4仍然以额定功率充电，SOC 缓慢升高。此外，与运行工况1 类似，除了EV4的α有所上升外，EV1—EV3的α均有不同幅度的下降。

由上述结果可知，本文所提控制策略可以根据电网频率波动、调频参与度因子的大小智能控制EV充放电，既考虑了用户的充电需求，又能为电网提供辅助调频服务。

3.3 模糊控制策略的效果验证

为了说明本文所提控制策略（下文简称本文策略）的优越性，在相同的仿真条件下将其与文献［17］中的控制策略（下文简称策略1）进行对比，并选择电网频率偏高的运行工况进行模拟，从而体现控制策略在应对极端情况时的能力。仿真条件设置如下：策略1 的充电因子在0～2 范围内变化，本文策略的调频参与度因子在0～1范围内变化，分别观察2种控制策略在频率偏差为±0.4 Hz时的功率响应特性。仿真结果见附录B 图B3。由图B3（a）可知，当频率偏差为0.4 Hz 时，应控制EV 充电。当策略1 的充电因子在0～1 范围内变化时，EV 先充电，然后充电功率逐渐减小为0，但充电功率变化不平滑，这是因为Mamdani 型模糊控制器的输出结果不连续，存在控制偏差；而本文策略的模糊输出是连续的，不存在控制偏差，因此其输出随调频参与度因子的增大而逐渐减小至稳定值，功率变化平滑。由图B3（b）可知，当频率偏差为-0.4 Hz 时，控制充电需求程度不高的EV 放电，同时控制充电需求程度高的EV 工作在不放电或以小功率充电的模式。当策略1 的充电因子在0～1 范围内变化时，模糊控制输出为0；而当充电因子大于1 时，EV 开始放电，放电功率随充电因子的增大而增大，但放电功率变化不平滑。当本文策略的调频参与度因子接近于0 时，对用户充电需求程度高的EV 以小功率充电，随着参与度因子的增大，EV 放电功率线性增大，大幅提高了控制的精度，且功率变化平滑。

3.4 多辆EV的调频作用验证

以附录B 图B4 所示的典型单区域电力系统调频模型为例，分析采用智能充放电控制策略接入电网的EV 对系统频率的影响。其中火电机组为系统的调频机组，原动机为非再热式汽轮机。

由于本文采用的是VSG 模型，在建立等效模型的过程中EV 调频模型需要反映VSG 的功率响应特性，本文采用EV 二阶惯性响应函数，如式（13）所示［17］。

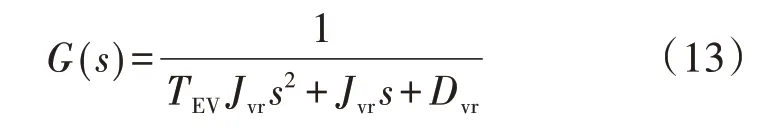
式中：TEV为VSG 的固有时间常数；Jvr、Dvr分别为VSG的等效虚拟惯量、等效虚拟阻尼。

EV 参与调频的模型如附录B 图B5 所示。仿真仍选取上述4 种具有代表性的EV，具体参数见附录B 表B3。基于本文所提EV 辅助调频模型，首先在阶跃负荷扰动下对策略1 和本文策略的调频效果进行仿真对比，设置在t=250 s时发生15 MW 的负荷突变，观察2 种控制策略下的系统频率响应，结果见图5（a）；然后在随机负荷扰动下对策略1 和本文策略的调频效果进行仿真对比，结果见图5（b）。

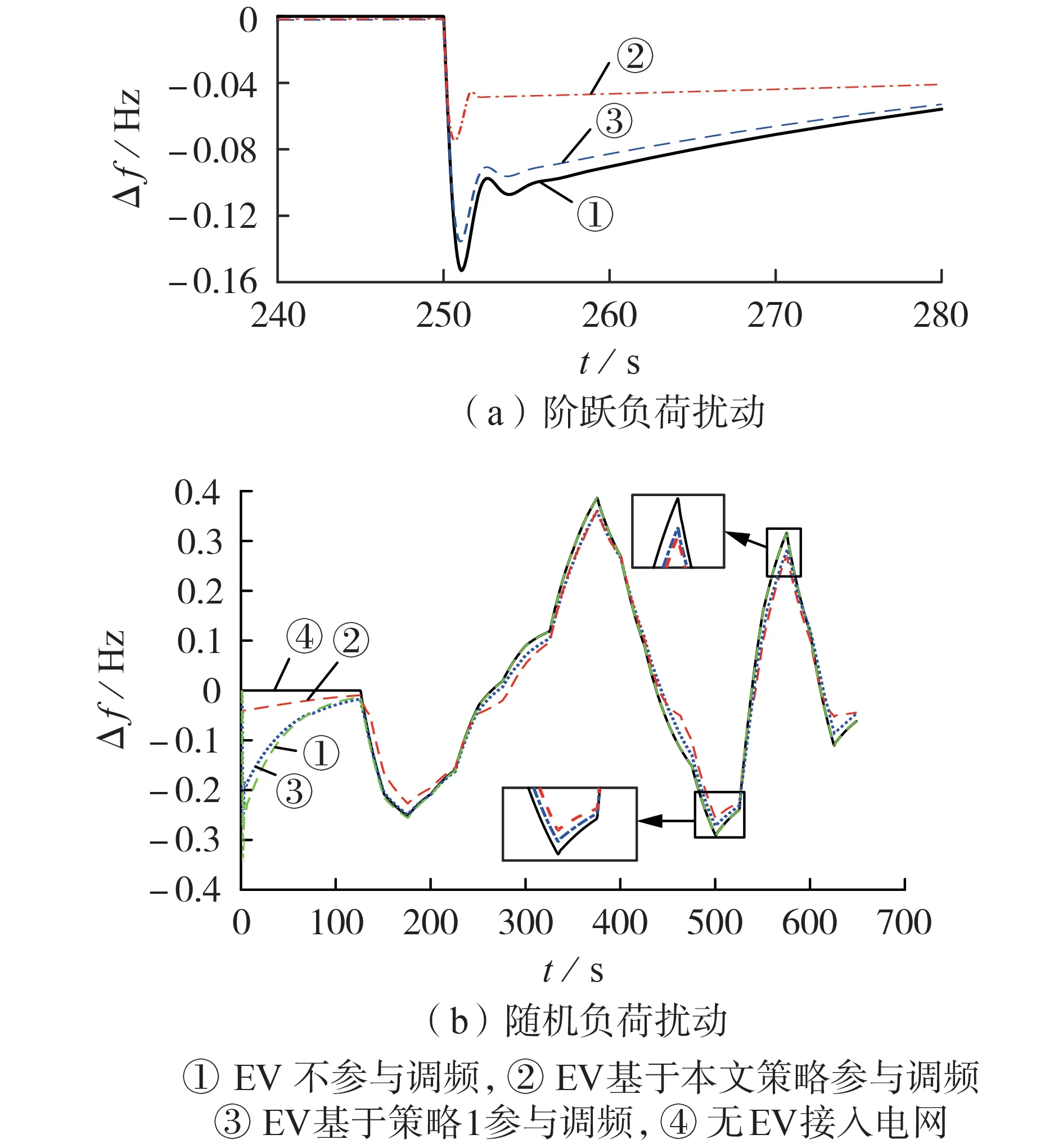
图5 多辆EV的调频效果Fig.5 Frequency regulation effect of multiple EVs

由图5（a）可以看出，当负荷突变增大时，相比策略1，采用本文策略时的系统频率偏差更小，因此本文策略的调频效果更好。这是因为当频率偏差小于0时，本文策略可以控制EV 向电网放电，而策略1只是减小了充电功率，EV 仍处于充电过程，相当于负荷。可见，在发生负荷突变增大时，采用本文策略的效果更好。由图5（b）可以看出，在［0，125］s 内，如果无EV 接入电网，则电网频率偏差为0；当大量EV在t=0 s 时接入电网但不参与调频时，相当于系统接入了大量负荷，电网频率会发生较大程度的跌落；而当EV 在t=0 s 时接入电网并参与调频时，相较于采用策略1，采用本文策略时的频率跌落明显更小。在电网负荷低谷（t=375 s 和t=575 s）时，策略1 与本文策略的调频效果相近，采用本文策略时的频率偏差稍小于采用策略1 时的频率偏差。而在电网负荷高峰（t=175 s 和t=500 s）时，由于采用本文策略的EV 可以向电网放电，补偿电网的功率缺额，而采用策略1 的EV 只是减小充电功率，因此采用本文策略时的频率偏差明显小于采用策略1 时的频率偏差。随着时间的推移，EV 接入但不参与调频的频率偏差变化曲线与无EV 接入时的频率偏差变化曲线逐渐重合，这表明由于系统自身的频率调节作用，原动机逐渐发出接入电网EV 所需的充电功率，EV 恒功率充电不再对电网的频率产生影响。

多辆EV 参与调频的仿真结果见附录B 图B6。由图可见：在电网高峰负荷时段，电网频率低于额定频率，EV1、EV2的α较大，可以参与电网的二次调频，因此电网负荷高峰时段该2 种类型的EV 按照α值的大小向电网输出功率，α值越大，则输出的功率越大，SOC 随之降低；而EV3、EV4的α很小，故这2 种类型的EV 均以额定功率充电，SOC随之升高。在电网负荷低谷时段，电网频率高于额定频率，需要EV 充电来储存电网中的剩余有功功率，α越小的EV，其充电功率越大，因此EV4的充电功率最大，EV1的充电功率最小，SOC均有不同程度的升高。

由上述仿真结果可以看出，采用本文策略的多辆EV接入频率波动的电网时，可以在满足用户充电需求的同时参与电网的辅助调频服务，减小了电网频率波动，有效地实现了“削峰填谷”。仿真进一步对本文策略与文献［17］所提控制策略进行了对比分析，仿真结果表明本文所提控制策略在发生阶跃负荷扰动以及随机负荷扰动时都能更加有效地减小频率偏差，提高电力系统的稳定性。