磁偏置超导故障限流器限流响应模型与并网运行研究
2021-11-20诸嘉慧韦德福秦汉阳朱义东严植泳陈盼盼张宏杰杨艳芳
诸嘉慧,韦德福,王 帅,秦汉阳,朱义东,严植泳,陈盼盼,张宏杰,杨艳芳,邹 军
(1. 中国电力科学研究院有限公司,北京 100192;2. 国网辽宁省电力有限公司电力科学研究院,辽宁 沈阳 110006;3. 北方工业大学 电气与控制工程学院,北京 100144;4. 清华大学 电机工程与应用电子技术系电力系统及发电设备控制和仿真国家重点实验室,北京 100084)
0 引言
随着我国电网规模的逐渐扩大,电网中的线路阻抗越来越小,一旦发生短路故障,将会对电力系统的安全性带来极大的影响。目前,在广州、上海等大型城市负荷中心已经出现断路器开断容量难以满足短路需求、采用高压等级的断路器又会增加成本的难题[1]。超导故障限流器SFCL(Superconducting Fault Current Limiter)集触发检测、快速限流和自我恢复功能于一身,是解决电网短路故障的一种有效方案[2-4],目前成为各国关注的热点。
近年来,国内外研究人员基于不同的限流原理,发展了多种针对电网应用的SFCL。耐克森公司研制出了被称为CURL10 的三相10 kV/10 MV·A 的电阻型SFCL,并在德国奈特芬市的莱茵韦斯特伐伦电力公司进行了并网试验[5]。2014 年,美国应用材料公司在纽约Knapps Corner 变电站安装并在网测试了15 kV/400 A的SFCL系统。日本、韩国也分别研制出了66 kV/0.75 kA的桥式SFCL[6-7]和22.9 kV/0.63 kA 的混合式单相SFCL[8]。我国正在开展面向实用化的超导故障限流技术研究。中国科学院电工所已研制出10.5 kV/1.5 kA 的三相桥路型SFCL 和40 kV/2 kA超导直流限流器原型样机[9-11]。北京云电英纳超导公司在云南普吉电站测试了35 kV/1.2 kA饱和铁芯型SFCL[12-13]。上海交通大学、华中科技大学也分别开展了纯电阻型和磁通约束型配电网级SFCL样机研究[14]。
本文将断路器的并联技术与SFCL相结合,基于高耦合分裂电抗器提出一种新型自触发磁偏置超导限流技术[15],可有效解决限流开断的问题。该SFCL由双分裂电抗器、无感型超导限流组件和快速开关组成,通过对开关进行控制,具有分级限流功能,可实现故障电流在首半波的限流响应和快速失超恢复。基于MATLAB/Simulink 软件搭建包含超导限流组件和双分裂电抗器的磁偏置SFCL 的10 kV 线路运行等效模型,理论分析了磁偏置SFCL在稳态运行以及在不同短路故障角下的限流运行性能,获得SFCL 限流过程中失超电阻和温度的变化规律,最后通过实验验证了限流特性。研究结果为磁偏置SFCL样机应用于电网的研究提供了重要的理论依据。
1 磁偏置SFCL运行系统设计
1.1 拓扑设计
磁偏置SFCL 拓扑如图1 所示[15]。回路系统主要由电网电源、线路阻抗(Rline和Lline)、磁偏置SFCL、负载阻抗(Rload和Lload)、线路断路器K2组成。其中,磁偏置SFCL 由高耦合双分裂电抗器(2 个绕组电感分别为L1和L2,L1=L2=L,互感M=αL,α为耦合系数)、无感型钇钡铜氧(YBCO)超导限流组件Rsc和快速开关K1三部分组成。双分裂电抗器同名端反向并联,超导限流组件Rsc分别与L2和快速开关K1串联,然后与L1并联。图1 中,Ia为回路总电流,I1为支路1 流经的电流,I2为超导限流组件支路(支路2)电流,且Ia=I1+I2。
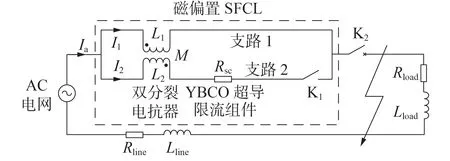
图1 SFCL系统拓扑Fig.1 Topology of SFCL system
1.2 运行原理和特色
正常运行时,磁偏置SFCL中超导限流组件为超导态,因此电阻为0;双分裂电抗器的2 个绕组由于反向相连,因此互感电压相互抵消,仅有漏抗接入回路中,对电网正常运行的影响不大。
当发生线路负载短路故障电流冲击时,磁偏置SFCL 将呈现逐级限流的特性,其故障限流过程分为2个阶段。第1阶段:在故障电流冲击下,I1和I2相应增大,当I2超过超导组件的临界电流时,YBCO 超导限流组件自动触发失超,迅速上升的失超电阻实现第1 级限流。第2 阶段:当YBCO 超导限流组件的电阻达到失超电阻值后,快速开关K1触发断开(通常在短路发生后10 ms)。此时,支路2 被断开,只剩支路1 接入回路,进行第2 级限流,直到故障电流减小到线路断路器K2的遮断容量,由K2切断回路。在完成故障电流首半波限流后,伴随支路2 被断开,YBCO 超导限流组件开始迅速恢复到超导状态,等待断路器K1的下一次闭合。
可见,该磁偏置SFCL具有如下特色:首先,在稳定运行时双分裂电抗器由于支路高度耦合使总压降较低,因此通流损耗比较小;其次,该SFCL具有支路分流能力,相比仅靠超导组件限流的方式,可以减小对YBCO 超导限流组件的通流要求,从而减少超导材料用量;再次,超导触发限流和恢复过程实现条件要求较低,不需要电力电子元件的控制信号,失超恢复较快;最后,能在故障电流首半波实现一级限流,在第2 个半波进行二级限流,具有数毫秒内限流响应速度,提高了SFCL的技术经济性。
1.3 运行状态方程
将双分裂电抗器进行支路解耦后,在正常运行状态下,由于YBCO 超导限流组件的阻抗一般是微欧级,并且双分裂电抗器两支路上的电抗产生的互感磁动势已经相互抵消,因此SFCL接入后基本不会对线路正常运行产生影响。SFCL 的稳态运行阻抗ZSFCL见式(1),正常稳态运行时ZSFCL随α的增加而线性减小,变化区间为[0,jωL/2],其中ω为角频率。

当线路发生短路故障后,2 条支路的电流I1和I2随之迅速增加,当I2超过了YBCO 超导限流组件的临界电流后,YBCO 超导限流组件逐渐开始失超,电阻上升,此时2 条支路的阻抗不再相等,导致I1>I2,互感磁动势不再相互抵消,这期间由双分裂电抗器和YBCO 超导限流组件共同限流,限流阻抗ZSFCL如式(2)所示,限流过程中ZSFCL随α的变化呈现复杂的非线性关系,而且考虑到Rsc为指数函数模型[16],所以限流过程中ZSFCL是一个复杂的双变量函数。
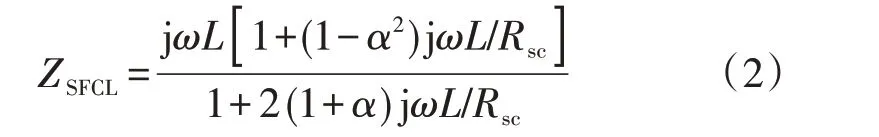
YBCO 超导限流组件在失超状态下会产生大量热量,为了保护YBCO 超导限流组件,快速开关K1在首半波完成限流后就立即断开(一般是10 ms 后)。故障电流将转移到双分裂电抗器的支路1 继续进一步限流,此时限流阻抗ZSFCL见式(3),直到回路电流达到线路断路器K2的遮断容量,K2断开故障线路。此过程中,ZSFCL与α无关,为支路1电抗。

2 基于MATLAB/Simulink的磁偏置SFCL磁热特性模型设计
考虑到基于单个超导失超特征值(n-value)的超导特征模型不能全面体现过流冲击时超导带材的电阻变化行为,为准确拟合超导带材随时间变化的失超过程,本文根据YBCO超导带材的电流密度J与临界电流密度Jc的倍数关系,提出了一种超导失超特征值时间分段等效法,实现了对超导材料非线性失超转变过程的细分化处理,完成了YBCO 超导限流组件磁热耦合建模,获得失超电阻的变化规律。
根据不同的临界电流倍数将整个通流过程划分为多个区间,因此每个区间可用不同的失超特征值n来等效。例如,将YBCO 超导带材的整个通流过程分为F个区间段,则对应的节点D=1,2,…,F-1,定义节点D处的电流密度JD=[1+2(D-1)]Jc,其中Jc为临界电流,如图2 所示。图3 为YBCO 超导带材电阻率ρYBCO的等效计算模型示意图。本文将超导带材等效为YBCO 超导层与金属稳定层的并联结构,采用失超特征值区间分段计算法,将YBCO 超导层电阻率用多个区间电阻率函数ρ1(J)、ρ2(J)、…、ρF-1(J)进行叠加等效,然后与金属稳定层电阻率ρstab并联,实现对YBCO超导带材电阻率的等效建模。

图2 通流区间分段模型Fig.2 Current-carrying segmented model

图3 YBCO超导带材电阻率等效计算模型Fig.3 Equivalent model of resistivity calculation of YBCO superconducting tape
所提出的超导通用等效电阻率分段函数见式(4)、(5),其中每个区间电阻率函数ρD(J)(D=1,2,…,F-1)对应的失超特征值为ni,由超导材料临界电流特性曲线测量获得。
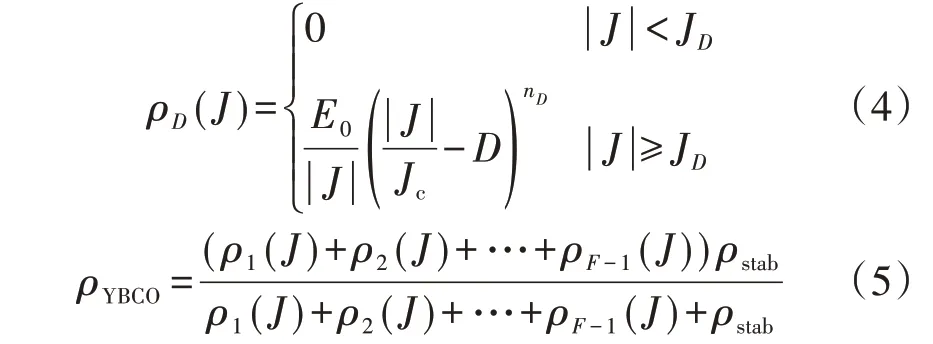
本文中,将磁偏置SFCL 中YBCO 超导带材的通流过程分为3个区间段和2个节点(即F=3),经计算可得2 个节点处的电流密度分别为J1=Jc和J2=3Jc,电阻率ρ1(J)、ρ2(J)分别见式(6)、(7),YBCO超导层电阻率为ρ1(J)和ρ2(J)的叠加。

式中:n1、n2和E0可以从文献[16]中得到;临界电流密度Jc由式(8)计算得到。
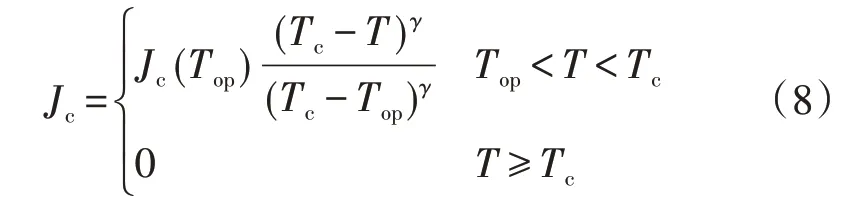
式中:Top为YBCO 超导带材在正常工作下的参考温度;Tc为超导带材的临界温度;γ为温度变化系数。
由此可知:
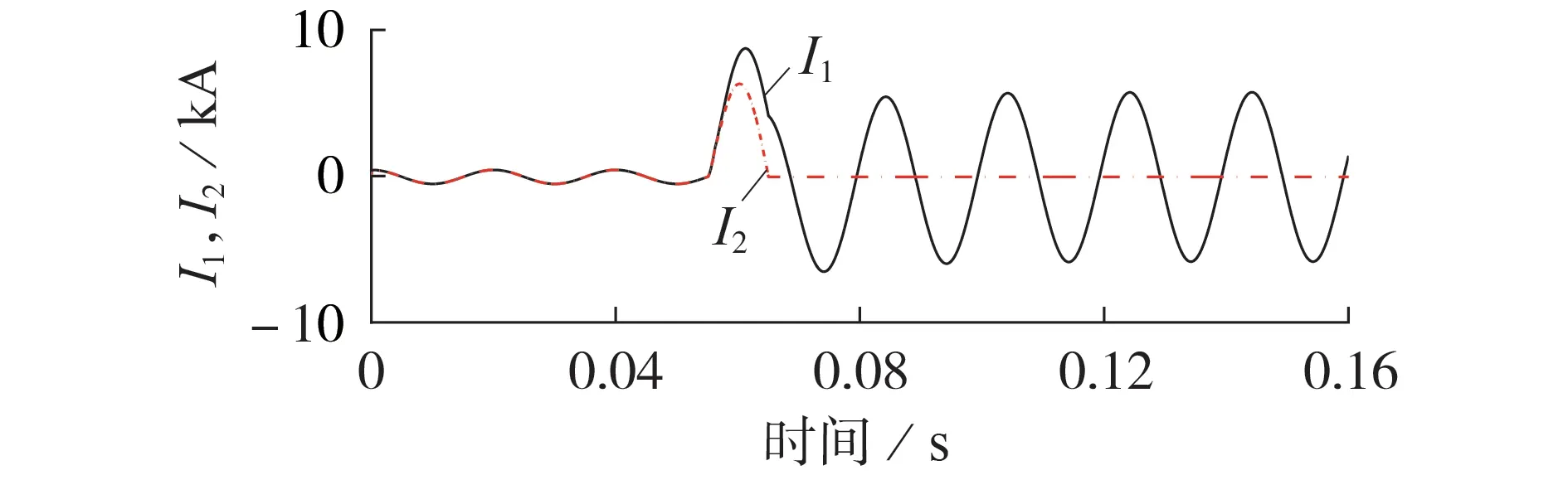
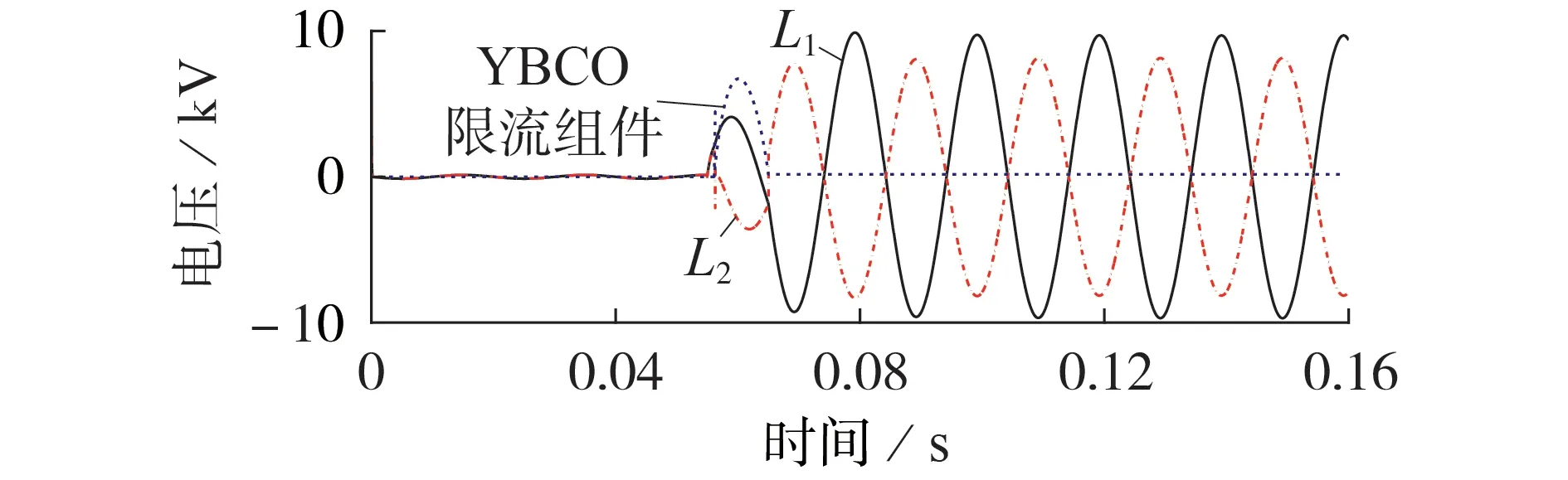
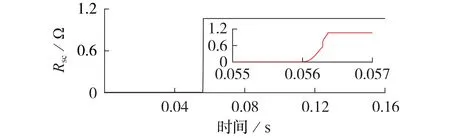
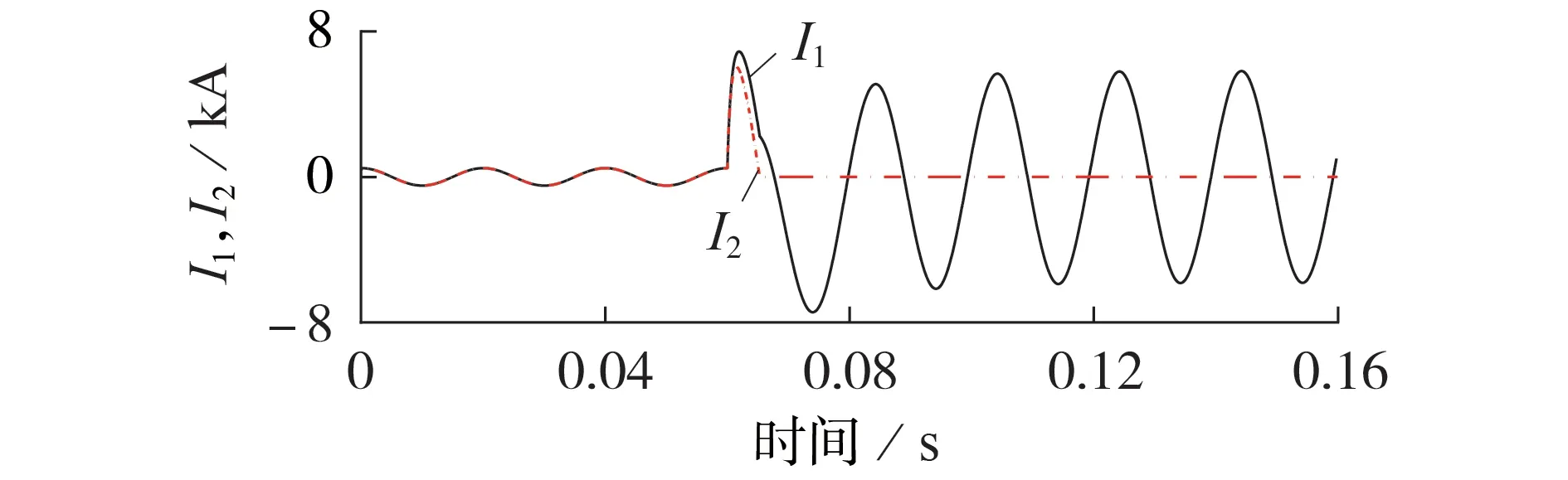
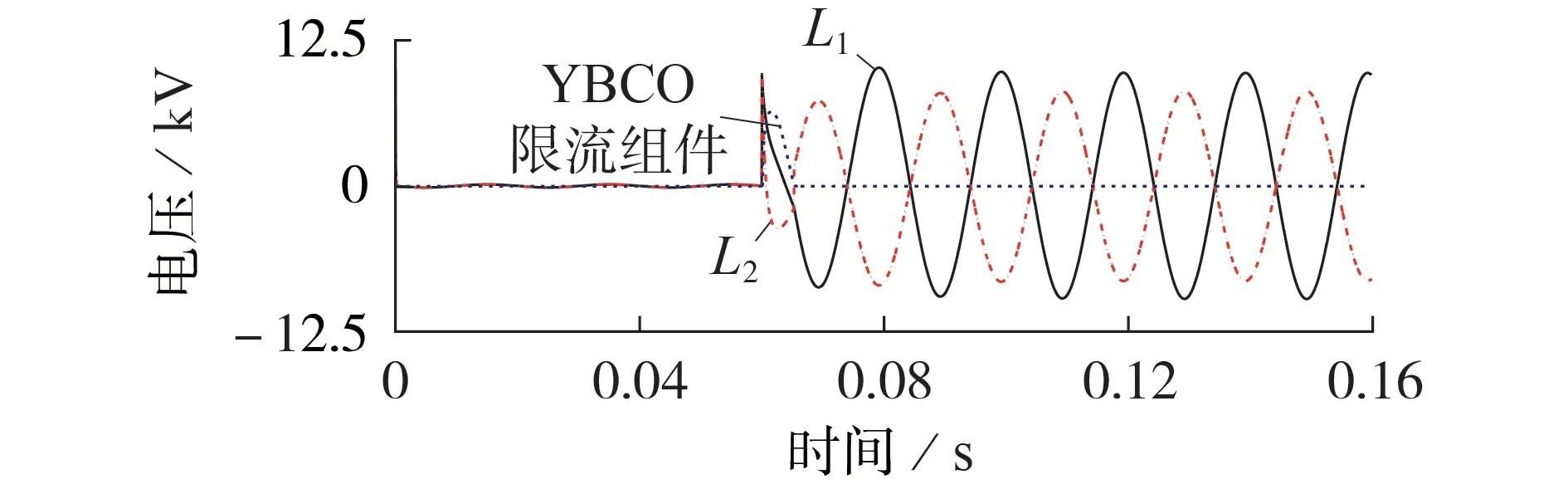
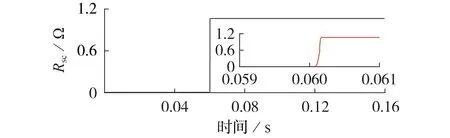
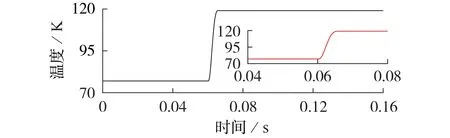
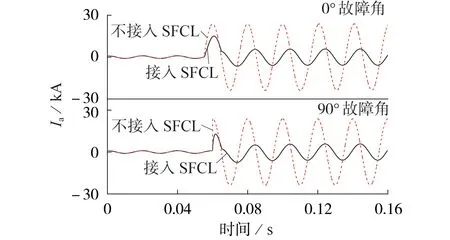
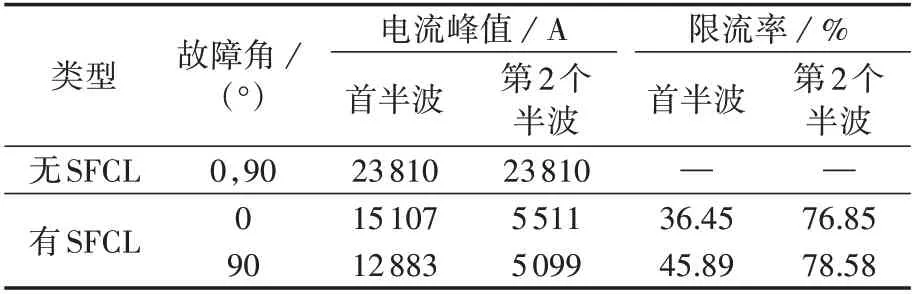
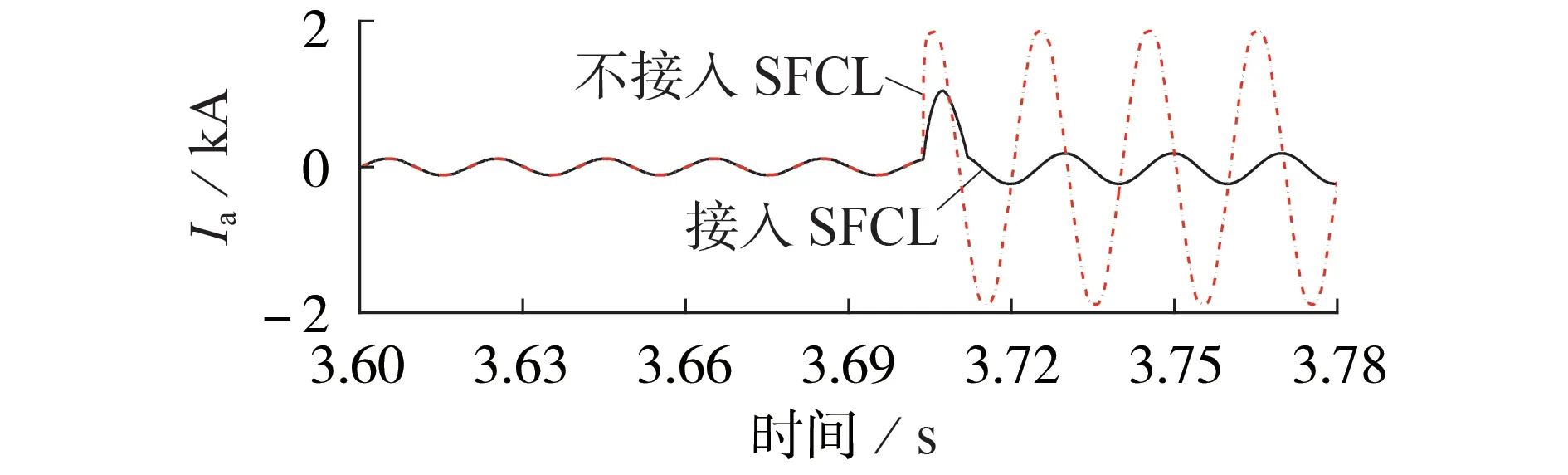
1)第1 区间,0 2)第2 区间,Jc≤J<3Jc,将ρ1(J)和ρ2(J)叠加后,此阶段采用n1值计算YBCO超导层电阻率; 3)第3区间,J≥3Jc,将ρ1(J)和ρ2(J)叠加后,此阶段采用n2值计算YBCO 超导层电阻率。考虑到此区间YBCO 超导带材中稳定层的电阻率ρstab小于YBCO超导层电阻率,故将进行分流。 此时,YBCO超导带材的等效电阻率ρYBCO为: 由于瞬间增大的电流密度会令超导材料进入高速失超传播状态[17],因此在大电流冲击下,单位长度YBCO 超导带材在时间t内产生的温度变化量ΔT见式(10)[18],被冷却介质带走的传热功率P见式(11)。 式中:I为电力线路电流有效值;h为对流换热系数;As为换热面积;h为对流换热系数;Top取77 K;t为每次计算时间间隔,由采样率确定;m=dA,为单位长度YBCO 超导带材的质量,d、A分别为YBCO 超导带材的密度和横截面积;cheat为YBCO 超导带材的比热系数,取cheat=241 J/(kg·K)[19]。 在大电流冲击瞬间,由于液氮汽化后会在超导带材周围形成氮气隔离区,不发生液氮换热。因此,本文中在故障电流冲击10 ms 期间,近似认为热平衡方程是绝热模型,即令式(11)中h=0。 假设某10.5 kV 负荷集中的电网结构可简化为图4 所示线路图,磁偏置SFCL 与线路阻抗Zline,负载阻抗Zload和线路断路器K2串联共同接入10.5 kV 母线,短路开关K3与Zload并联,通过触发K3闭合,实现10.5 kV线路负载短路故障。 图4 磁偏置SFCL并网系统模型Fig.4 Model of grid-connected system with magneto-biased SFCL 磁偏置SFCL 采用YBCO 涂层导体的材料参数见附录A 表A1,系统运行仿真参数见附录A 表A2。应用MATLAB/Simulink软件,建立的含磁偏置SFCL的10.5 kV 并网运行系统的仿真模型见附录A 图A1。其中通过改变变压器副边接线方向模拟双分裂电抗器同名端反接关系,YBCO 超导限流组件使用S-Function 模拟超导电阻暂态磁热耦合变化过程(见式(6)—(11)),从而实时控制YBCO 超导限流组件失超电阻输出[20-22]。 当短路开关K3闭合,线路发生负荷短路故障10 ms 后,快速开关K1在检测到回路电流过零点时立即断开支路2,故障电流转移到双分裂电抗器支路1 中,研究此过程中SFCL 在不同短路故障角下的限流效果。设定YBCO 超导限流组件临界电流为1 kA,仿真时长为0.16 s。分别在0.055 s 和0.06 s发生负荷短路,利用2个时刻的故障电流为0和最大值,来模拟0°和90°这2种极端故障角的限流运行情况,并评价限流效果。为简化模型,将负载阻抗Zload设置为阻性负荷,产生的故障电流峰值为23.81 kA。 3.2.1 SFCL最小故障角限流特性 在t=0.055 s 时,触发0°最小故障角短路。图5为故障限流过程中,SFCL 中双分裂电抗器2 条支路的电流波形。由图可知,系统发生短路故障后,支路1 和2 在故障初始时期继续进行均流,但在t=0.058 s(即短路故障发生3 ms 后),YBCO 超导限流组件失超产生的电阻大于支路1 的阻抗,故障电流便不再均匀地流过2 条支路,而是偏移到了阻抗较小的支路1,当t=0.065 s 时,YBCO 超导限流组件所在支路在故障触发10 ms 被断开后,故障电流全部转移到支路1,此时支路2的电流降为0。 图5 SFCL中2条支路电流曲线(0° 故障角)Fig.5 Current curves of two branches in SFCL when fault angle is 0° 图6 为故障限流过程中,SFCL 中双分裂电抗器2条支路的电压和YBCO 超导限流组件的电压波形。由图可知,双分裂电抗器的2 条支路电压互为反向,而在t=0.065 s时切除支路2后,L2上仍然有感应电压存在,并且与L1的电压大小相等、方向相反。YBCO超导限流组件的电压在故障限流的10 ms 内,随失超电阻的产生而产生,当支路2 的电流降为0 后,其电压也降为0。 图6 SFCL各组件电压曲线(0°故障角)Fig.6 Voltage curves of components in SFCL when fault angle is 0° YBCO 超导限流组件在故障触发后的失超电阻波形如图7所示。在发生了近乎24倍故障电流冲击下,YBCO 超导限流组件立刻进入高速失超传播状态,失超电阻在短路故障触发时刻(即t=0.055 s)后的0.35 ms 内,迅速增加到1.06 Ω 设计值,并保持稳定。而且,失超电阻的增长率随故障电流的增加而变大,失超电阻导致了双分裂电抗器的2 条支路不再均匀分流。 图7 YBCO超导限流组件失超电阻变化波形(0°故障角)Fig.7 Variation curve of quench resistance of YBCO superconducting unit when fault angle is 0° 图8 为YBCO 超导限流组件在0°故障角短路电流冲击下的温度变化过程。随着YBCO 超导限流组件的失超电阻增加,温度从77 K 逐渐增大,由于限流期间近似为绝热环境,所以在t=0.064 s,即短路故障发生9 ms后,温度上升到146 K就一直保持不变。 图8 YBCO超导限流组件温度变化波形(0°故障角)Fig.8 Variation curve of temperature of YBCO superconducting unit when fault angle is 0° 3.2.2 SFCL最大故障角限流特性 在t=0.06 s 时,触发90°最大故障角短路故障。图9 为该故障限流过程中,SFCL 中双分裂电抗器2条支路的电流波形。由图可知,短路时刻支路1和2的电流为最大值,伴随YBCO 超导限流组件产生失超电阻,2 条支路电流不再均流分布,在t=0.07 s(即故障触发10 ms后),支路2被断开,故障电流全部转移到支路1,此时支路2 的电流变为0。这些变化过程与0°故障角的变化规律一致,但发现首半波中支路1和2的电流峰值下降更明显。 图9 SFCL的2条支路电流曲线(90°故障角)Fig.9 Current curves of two branches in SFCL when fault angle is 90° 图10 为SFCL 中双分裂电抗器的2 条支路的电压和YBCO 超导限流组件的电压波形,其变化规律与0°故障角的情况相似。但在t=0.06 s,由于故障触发瞬间短路电流为最大值,电流突变导致双分裂电抗器的L1和L2上都产生了尖峰脉冲电压干扰,会对超导绕组绝缘带来影响。 图10 SFCL各组件电压曲线(90°故障角)Fig.10 Voltage curves of components in SFCL when fault angle is 90° YBCO 超导限流组件在故障触发后的失超电阻波形如图11 所示。由图可知,尽管稳定后的超导失超电阻值仍为1.06 Ω,但90°故障角下的失超过程更短,失超电阻在短路故障触发时刻(即t=0.06 s)后的0.2 ms 内增加到1.06 Ω,其增长速度是0°故障角时的1.75倍。可见短路故障角对失超电阻的变化过程具有较大的影响。 图11 YBCO超导限流组件失超电阻变化波形(90°故障角)Fig.11 Variation curve of quench resistance of YBCO superconducting unit when fault angle is 90° 图12 为90°故障角短路电流冲击下YBCO 超导限流组件的温度变化波形。由图可知,相比于0°故障角的情况,由于失超电阻增加速度加快,使得故障电流限制效果更好,因此回路电流峰值更小,由失超电阻产生的热功率也相应变小,因此YBCO 超导限流组件的温度反而变小。同理在绝热条件下,在t=0.066 s(即短路故障发生6 ms 后),温度上升到120 K 保持不变,相比于0°故障角的最高温度146 K,温度降低了17.8%。 图12 YBCO超导限流组件温度变化波形(90°故障角)Fig.12 Variation curve of temperature of YBCO superconducting unit when fault angle is 90° 图13为有、无SFCL作用的回路总电流波形对比图。由图可知:在0°故障角下,SFCL接入后,故障电流首半波的电流峰值从23810 A减小到15107 A,首半波之后(即t=0.065 s),电流峰值继续减小到5511 A;在90°故障角下,SFCL接入后,首半波的电流峰值减小到12 883 A,在首半波后的电流峰值继续减小到5 099 A,故障限流效果好于0°故障角的情况。 图13 接入SFCL前、后回路总电流波形对比Fig.13 Comparison of current curves between with and without SFCL 定义磁偏置SFCL的限流率k为: 式中:ifault为故障电流波形峰值;ilimit为SFCL接入后的电流波形峰值。 表1为磁偏置SFCL在0°和90°故障角下的限流率比较。SFCL 在首半波将故障电流限制下来之后,继续通过双分裂电抗器中L1限流的效果也十分明显。在给定负载条件下,90°故障角下的首半波限流率为45.89%,第2 个半波的限流率达到78.58%,比0°故障角下首半波的限流率36.45%大了9.44%,而且从图13 中可知,由于90°故障角下线路短路电流波形中存在一些非周期分量,导致电流波形向下偏移,因此在支路1接入时,该时刻电流峰值比0°故障角下的值要小一些,但很快伴随非周分量衰减结束,二者电流波形峰值趋于相同。同时可见,快速开关K1的分断电流不足故障电流的1/2,在超导支路断开之后的电流值相比无SFCL时的电流下降明显,从而可以降低线路断路器K2的遮断容量。从上述仿真结果可知,SFCL 在不同故障角下都产生了良好的限流效果,其中90°故障角的限流效果更加明显,较好地实现了逐级限流的设计目的。 表1 不同故障角下限流率比较Table 1 Comparison of current limiting rates under different fault angles 为了验证磁偏置SFCL 的限流性能,进行了工频过电流冲击实验。限流实验平台如附录A 图A2所示,主要包括试验电源、无感超导单元、双分裂电抗器、实时监控系统、低温液氮罐、负载电阻柜和快速开关。限流试验分为2 个阶段:首先,在没有SFCL 接入下测量发生负载短路故障时的回路总电流;然后,将SFCL 接入电路,在相同的故障条件下测量限流情况。图14 为触发90°故障角下的回路总电流实验波形,在没有SFCL 接入的情况下,短路电流峰值为1 838 A,接入SFCL 后,首半波限流率k=(1 838-1 040)/1 838=43.4%,第2 个半波限流率k=(1 838-190)/1 838=89.66%,两级限流效果显著,且与仿真规律非常相似,验证了所提磁偏置SFCL拓扑的有效性和故障响应模型的正确性。 图14 回路总电流实验波形(90°故障角)Fig.14 Experimental waveforms of circuit current when fault angle is 90° 针对电网短路故障限流问题,本文提出了一种自触发阻感混合式的磁偏置SFCL 拓扑结构,建立了基于失超电阻率分段模型的含磁偏置SFCL 的10.5 kV 并网系统仿真模型,获得了电网不同短路故障角下SFCL 的磁热特性和回路电流的变化规律。本文得到的主要结论如下。 1)磁偏置SFCL 的拓扑结构能够实现逐级限流效果,快速开关K1的分断电流不足故障电流的1/2,能有效降低线路断路器的遮断容量,具有较好的技术经济性。 2)磁偏置SFCL 在90°故障角下的限流效果更加明显,首半波的限流率为45.89%,第2 个半波的限流率达到78.58%。失超电阻变化率随故障电流的增加而增大,90°故障角下的失超限流电阻的变化率是0°故障角下的1.75 倍;由于限流率较大,90°故障角下由热积累产生的温度最大值相比0°故障角时降低了17.8%。 3)当线路主要为阻性负载,额定工况下发生短路故障时,线路中的自由分量较小,SFCL 可使线路很快趋于稳定。 4)工频过电流冲击实验结果验证了所提磁偏置SFCL的逐级限流性能和限流响应模型的正确性。 笔者后续将进一步研究传热条件下YBCO 超导限流组件的失超恢复过程。 附录见本刊网络版(http://www.epae.cn)。
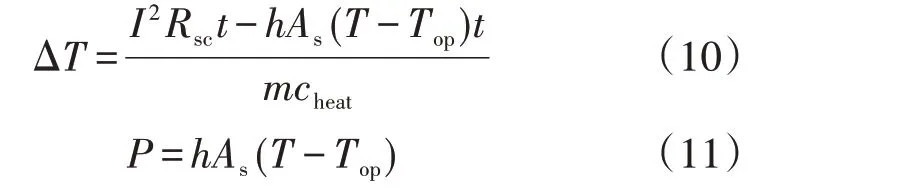
3 磁偏置SFCL运行仿真与结果分析
3.1 含磁偏置SFCL的10.5 kV并网系统模型

3.2 SFCL限流过程仿真与分析

3.3 SFCL故障限流率比较

4 实验与结果
5 结论
