基于Bezier曲线的CIGS薄膜光伏电池I-V曲线简单拟合方法
2021-11-20朱显辉苏勋文
师 楠,朱显辉,苏勋文
(1. 黑龙江科技大学 工程训练与基础实验中心,黑龙江 哈尔滨 150022;2. 黑龙江科技大学 电气与控制工程学院,黑龙江 哈尔滨 150022)
0 引言
薄膜光伏电池和传统的硅基电池相比,具有节省材料、理论效率高和便于安装等优点,因此备受重视,被称为第2 代光伏电池技术,其正在成为当前光伏电池产业的主要发展方向之一[1-2]。
目前铜铟镓硒(CIGS)薄膜光伏电池是薄膜光伏电池中效率最高的模块之一。据不完全统计,截至2019年5月,凯盛科技和神华等企业的CIGS 商业化模块的光电转换效率约为16%,汉能集团的CIGS模块的实验室光电转换效率已达到了22.9%[1]。CIGS模块的商业化进程正处于起步阶段,虽然目前市场份额不多,但发展迅猛。
CIGS 等薄膜光伏电池从生产材料到制备工艺等均与硅基电池有较大的差异,该差异导致CIGS 模块的电流-电压输出特性与硅基光伏模块不同[3-4]。鉴于CIGS薄膜光伏电池的电流-电压输出特性曲线(即I-V曲线)是进行光伏最大功率点跟踪、故障检测和经济效益评估的必要前提,对其进行研究具有的重要理论和现实意义[5]。
在CIGS 模块商业化进程的起始阶段,CIGS 模块I-V曲线的建模问题得到了重点关注。例如文献[6]利用现场实测的方式给出了CIGS 模块的I-V曲线的特点;文献[7-8]分别分析了老化和阴影对CIGS模块输出特性的作用效果;文献[9]讨论了温度对CIGS 模块输出特性的影响规律;文献[10]提出了一种利用四参数超越方程描述CIGS 模块输出特性的方法,文献[11]利用简化超越方程求解CIGS 模块的I-V曲线,并尝试利用最大功率点对精度进行校验,但文献[10-11]采用的迭代等数值求解方法需要大量的仿真时间;文献[12]通过大量实测数据探讨了双二极管模型中二极管的扩散电流和复合电流随辐照度的变化规律,文献[13]提出了一种无需实验,仅利用厂商给定数据的差分进化算法计算双二极管模型的7个未知参数,文献[12-13]重点是对CIGS模块的超越方程的未知参数进行求解,并未给出对应的I-V曲线,因此无法直接应用于最大功率点跟踪等工程实践中。
为解决上述问题,本文利用Bezier 曲线优良的数据拟合能力,提出一种利用2条二阶Bezier曲线直接拟合CIGS 薄膜光伏电池的I-V曲线的简单方法,并以通过弦截法迭代求解的数值结果为基准,将拟合结果和文献[10]的建模结果进行了对比分析,验证了所提方法的准确性。和已有的CIGS 薄膜光伏电池建模方法相比,本文所提方法无需任何实验测试数据,也无需对超越方程的参数进行迭代等数值求解,仅利用厂商数据即可直接给出CIGS 薄膜光伏电池的I-V曲线,计算简单、耗时较短,且精度较高。
1 基于Bezier曲线的光伏电池建模方法
文献[14]提出了利用Bezier 曲线拟合光伏电池I-V曲线的方法,本节对其进行简要说明。
1.1 采用2条Bezier曲线拟合I-V曲线的基本思路
Bezier 曲线拟合的基本思路是利用一条光滑曲线逼近预先确定的空间数据点位置,由伯恩斯坦基函数构造的Bezier曲线表达式φ(x,y)如式(1)所示。
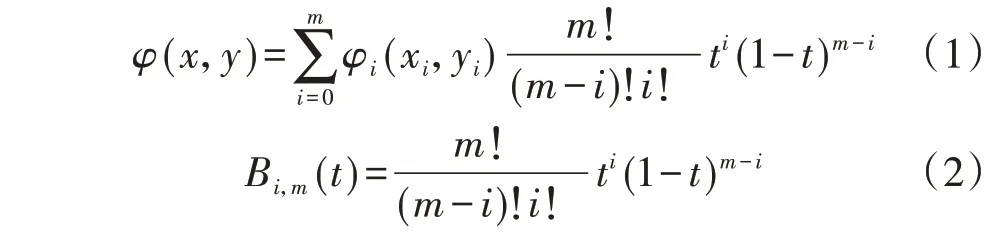
式中:m为Bezier曲线的阶数;φi(xi,yi)为Bezier曲线中的控制点;0≤t≤1;Bi,m(t)为伯恩斯坦基函数。
给定式(1)中的控制点φi(xi,yi),t取[0,1]范围内的任一个数值都可以得到1 个φi(xi,yi),遍历[0,1]范围内的t值后,即可得到Bezier曲线的轨迹。
由Bezier曲线的端点性质可知,当t=0和t=1时,Bi,m(t)=1,则式(1)满足:
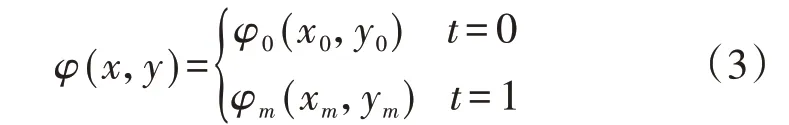
式(3)表明Bezier 曲线通过且仅通过第1、m+1个控制点,即Bezier曲线通过其起点和终点。
为了保证Bezier 曲线通过CIGS 薄膜光伏电池的短路电流点、最大功率点和开路电压点,以一条Bezier 曲线拟合CIGS 薄膜光伏电池的I-V曲线的最大功率点左侧的输出特性,并将短路电流点和最大功率点作为本条Bezier 曲线的起点和终点;以另一条Bezier 曲线拟合I-V曲线的最大功率点右侧的输出特性,并将最大功率点和开路电压点作为该条Bezier曲线的起点和终点,以得到较好的拟合效果。
1.2 Bezier曲线控制点的讨论
进一步分析式(1)可知,Bezier 曲线的阶数m越大,控制点的数量和曲线的计算就越复杂。考虑到一阶Bezier 曲线为一条直线,无法满足要求,为保证计算的简单性,本文采用二阶Bezier 曲线对CIGS 薄膜光伏电池I-V曲线进行拟合。
2 条Bezier 曲线相交于最大功率点,保证2 条曲线在交点处的平滑过渡,对CIGS 薄膜光伏电池的最大功率点跟踪和性能评估至关重要。为此,本文所提方法构造经过最大功率点,且与经过开路电压点和短路电流点的直线平行的直线,在该直线上寻找Bezier 曲线控制点。通过在所构造的直线上选取2条二阶Bezier 曲线的控制点,使2 条Bezier 曲线在交点处的一阶导数均为0,满足一次导数相等的条件,确保了2条Bezier曲线的平滑过渡。
为了进一步明确Bezier 曲线的控制点对曲线的影响规律,给出基于不同控制点得到的二阶Bezier曲线如图1所示。图中,L为连接开路电压点KU(Voc,0)和短路电流点KI(0,Isc)的直线,Voc、Isc分别为开路电压点的电压值、短路电流点的电流值;LP为经过最大功率点KP(Vm,Im)的直线,且LP与L平行,Vm、Im分别为最大功率点对应的电压、电流值;LG为假定的实际光伏I-V曲线。以最大功率点KP右侧曲线为例,分别以最大功率点KP(Vm,Im)和开路电压点KU(Voc,0)作为二阶Bezier 曲线的起点和终点,选取LP上的C1和C2作为控制点时,可分别得到Bezier 曲线LC1和LC2。由图1 可见,控制点与最大功率点KP(Vm,Im)的距离越小,所得Bezier 曲线的凹特性越显著,否则凸特性就越显著;最大功率点左侧的Bezier曲线的拟合效果和右侧类似,此处不再赘述。
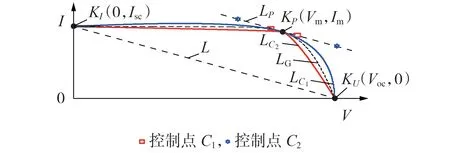
图1 基于不同控制点得到的Bezier曲线Fig.1 Bezier curves based on different control points
由上述分析可知,通过选择适当的控制点可以找到能够较好地拟合CIGS 薄膜光伏电池的I-V曲线的Bezier 曲线,从而精确刻画CIGS 薄膜光伏电池的输出特性。
2 定端点弦截迭代求解的参考基准
为了讨论Bezier 曲线对CIGS 薄膜光伏电池I-V曲线的拟合效果,需给出误差分析的参考基准。文献[15]已经考察了以迭代求解的数值结果作为误差分析基准的可行性。本节基于五参数超越方程,同样利用迭代法求解CIGS 薄膜光伏电池的I-V曲线,并将迭代求解的数值结果作为分析Bezier 曲线拟合误差的基准。
若要求解CIGS 薄膜光伏电池I-V曲线的数值解,则需要已知超越方程的5 个未知参数,但厂商数据手册并未给出这5 个未知参数的值[16]。为此,首先利用定端点弦截迭代算法对超越方程的5 个未知参数进行求解。忽略影响较小的常数项后,CIGS 薄膜光伏电池的超越方程形式如式(4)所示。
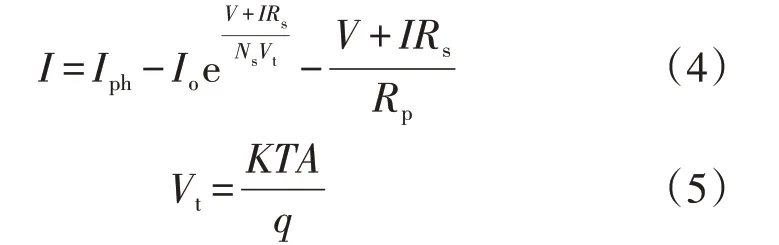
式中:Iph为光生电流;Io为二极管暗电流;Ns为串联电池数;Rs为二极管串联电阻;Rp为二极管并联电阻;Vt为PN 结热电压;K为Boltzmann 常数;T为二极管结温(单位为K);A为二极管品质因子;q为电子电量。
为求解式(4)中的Iph、Io、Rs、Rp和A,将厂商数据手册给定的短路电流点KI(0,ISC)和开路电压点KU(Voc,0)代入式(4)可得:

基于式(6)、(9)、(11)—(13)可求解CIGS 薄膜光伏电池的超越方程的5 个未知参数。其中,式(11)—(13)为隐函数形式,需要以定端点弦截法进行求解。定端点弦截法是一种以牛顿迭代为基础的改进数值计算方法,其基本思路是利用2 个确定点之间的差商代替牛顿迭代法中的一阶导数,以避免复杂的偏导数求解过程,其迭代求解通式见式(14)。
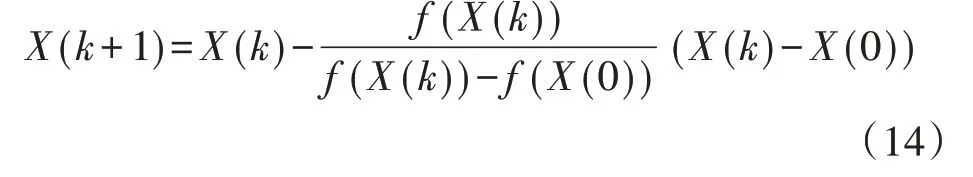
式中:X(k)和X(k+ 1)分别为第k次和第k+1 次迭代解,k=1,2,…;X(0)为迭代初始值;f(·)为待求解的函数。
利用定端点弦截法对CIGS 薄膜光伏电池超越方程参数进行迭代求解时,需要对式(11)—(13)进行适当的变换,将Vt、Rs和Rp代替式(14)中的X,即可实现Vt、Rs和Rp的迭代求解。以Rs为例,定端点弦截法需要2 个初值,所以需要预先给定Rs(0)和Rs(1),定端点弦截法求解流程图见附录A图A1。
利用定端点弦截法对7 种不同的CIGS 薄膜光伏电池的超越方程进行求解,得到超越方程的5 个未知参数的求解结果如表1所示。
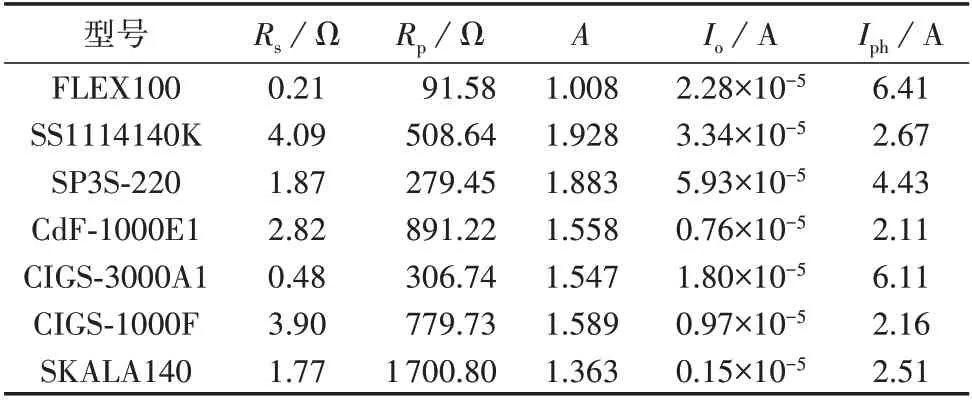
表1 CIGS薄膜光伏电池的超越方程的未知参数求解结果Table 1 Solutions of with unknown parameters for transcendental equation of CIGS thin-film photovoltaic cells
利用表1 可以得到参数已知的CIGS 薄膜光伏电池的超越方程形式。值得注意的是,此时需再次利用定端点弦截法对参数已知的超越方程进行迭代求解,才能得到CIGS 薄膜光伏电池的I-V曲线的数值解,并将其作为Bezier 曲线的拟合误差分析基准。该过程与超越方程的未知参数求解过程类似,本文不再赘述。
3 Bezier曲线控制点拟合规律
基于第1 节中的方法,利用Bezier 曲线对表1 中的CIGS 薄膜光伏电池的I-V曲线进行拟合,通过调节控制点的位置,得到不同精度的I-V曲线,从中选择精度最高的I-V曲线作为最佳拟合结果。以迭代计算结果为基准,分析最佳拟合结果的误差,结果如表2 所示。表中,emax和eav分别为拟合最大相对误差和平均相对误差。由表2 可见,Bezier 曲线对7 种不同的CIGS 薄膜光伏电池的拟合最大相对误差均小于1.8%,平均相对误差均小于1%,达到了较高的拟合精度。
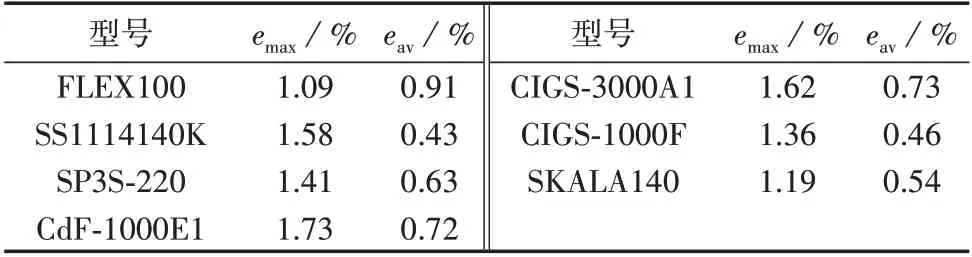
表2 Bezier曲线拟合误差Table 2 Error of Bezier function fitting
为探索拟合结果最佳的Bezier 曲线的控制点分布规律,给出基于某控制点得到的Bezier曲线如图2所示。图中,KIC(VC,IC)为控制点,(VC,IC)分别为控制点的坐标;O1(Vo,Io)为过KIC(VC,IC)所作的横轴的垂线与过KP(Vm,Im)所作的纵轴的垂线的交点,(Vo,Io)为交点的坐标。
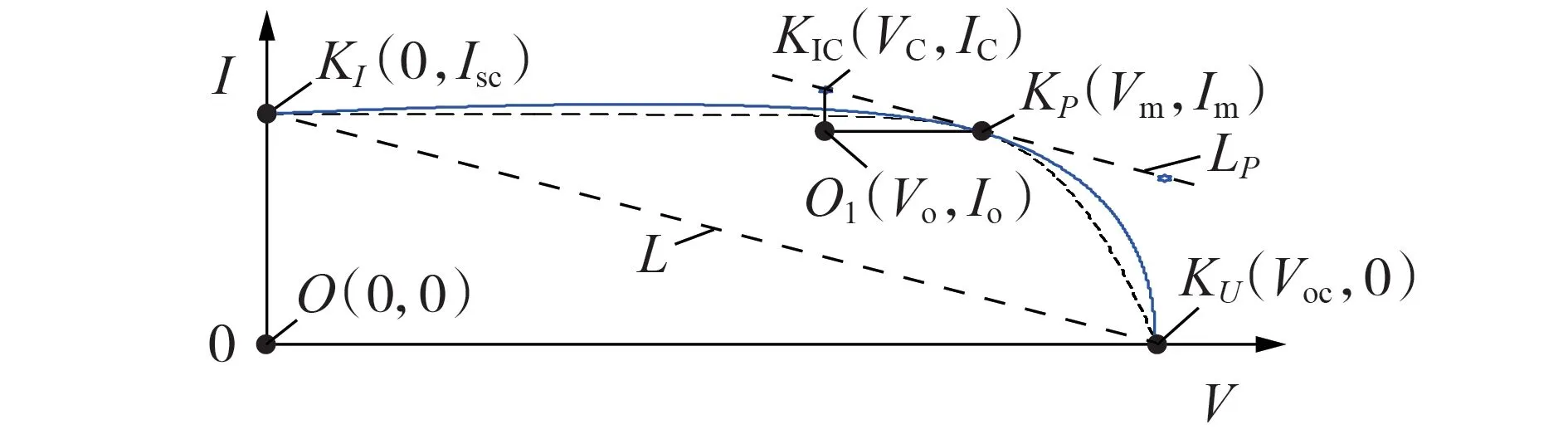
图2 基于某控制点得到的Bezier曲线Fig.2 Bezier curves based on a control point
由第1节分析可知,Bezier 曲线控制点的位置决定了曲线的凹凸程度,在图2 所示情况下,控制点距离最大功率点KP(Vm,Im)越远,Bezier 曲线的凸特性越显著。同时,考虑到光伏电池的填充因子FFF是能够全面表征CIGS 薄膜光伏电池I-V特征的系数,满足:

由图2可以看出,△KIOKU和△KICO1KP呈相似关系,因此,可按照相似三角形的性质确定Bezier 曲线控制点的位置,以简化分析和计算过程。
综合分析上述因素,本文选取控制点KIC(VC,IC)与最大功率点KP(Vm,Im)的距离LICP以及短路电流点KI(0,Isc)与开路电压点KU(VOC,0)的距离LIU之比作为纵坐标,以FFF作为横坐标,得到KP(Vm,Im)左、右两侧曲线控制点位置与FFF之间关系的拟合规律如图3所示。图中,λf和λr分别为KP(Vm,Im)左、右两侧的LICP与LIU之比。
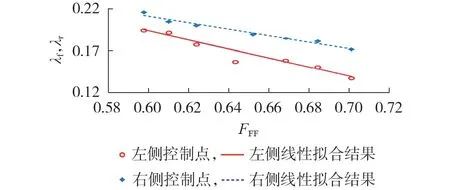
图3 7种CIGS薄膜光伏电池控制点拟合规律Fig.3 Fitting law of control points of seven CIGS thin-film photovoltaic cells
进一步给出λf、λr与FFF之间的拟合规律分别如式(16)、(17)所示。

基于式(16)、(17)可以得到最大功率点左、右侧控制点与最大功率点的距离,进而得到控制点的坐标,从而得到对应的Bezier 曲线用于拟合CIGS 薄膜光伏电池的I-V曲线。本文方法无需进行任何实验,仅利用厂商数据手册给定的参数即可有效拟合不同厂家和型号的CIGS薄膜光伏电池的I-V曲线。
4 拟合规律的验证
为验证式(16)、(17)所示的拟合规律,重新选取4 种不同厂家和型号的CIGS 薄膜光伏电池的I-V曲线进行拟合,4种电池的型号、参数如表3所示。

表3 4种CIGS薄膜光伏电池的型号和参数Table 3 Types and parameters of four CIGS thin-film photovoltaic cells
将本文的拟合结果与文献[10]的求解结果进行对比分析。文献[10]利用简化的四参数模型和迭代求解建立了CIGS 薄膜光伏电池的输出特性曲线,具体形式如式(18)所示。

式中:Rs和A的计算公式分别如式(19)和式(20)所示。

将厂商给定的数据代入式(18)—(20)中,可得到CIGS 薄膜光伏电池I-V曲线的超越方程,利用MATLAB 的fsolve函数进行迭代求解,即可得到文献[10]的求解结果。
基于表3 中的厂商给定参数,利用式(16)、(17)分别确定2条二次Bezier曲线控制点位置,进而利用Bezier曲线实现CIGS薄膜光伏电池的I-V曲线拟合。将所得Bezier 曲线和文献[10]的求解结果与本文第2节所得的参考基准进行对比,结果如图4所示。进一步分析图4 中的Bezier 曲线拟合结果和文献[10]的求解结果与参考基准的误差,结果如表4所示。

图4 4种CIGS薄膜光伏电池的拟合结果Fig.4 Fitting results of four CIGS thin-film photovoltaic cells
由表4 可见,本文方法对4 种CIGS 薄膜光伏电池的I-V曲线的拟合最大相对误差小于2%,平均相对误差小于0.8%,均小于文献[10]对应的误差。另外,本文方法针对1000个数据点的平均计算时间为72 ms,文献[10]方法针对501 个数据点的平均计算时间为20.4 s。可见,与传统方法相比,本文方法不仅精度更高,且计算过程简单、耗时更短,降低了计算成本。
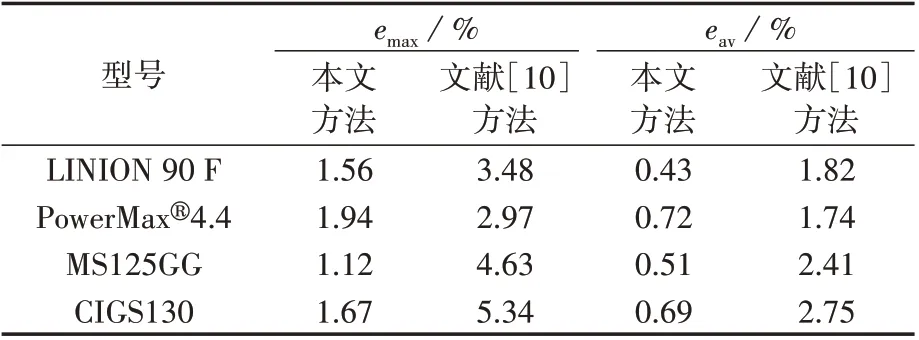
表4 4种CIGS薄膜光伏电池的拟合误差Table 4 Fitting erros of four CIGS thin-film photovoltaic cells
5 结论
本文主要利用厂商给定数据,采用Bezier 曲线拟合CIGS 薄膜光伏电池的I-V曲线并进行验证,主要贡献如下:
1)明确了利用2 条二阶Bezier 曲线对CIGS 薄膜光伏电池的I-V曲线进行拟合的思路,进一步探讨了控制点位置对Bezier曲线形状特点的影响效果;
2)构建了定端点弦截迭代算法的误差分析基准,并分别实现了对CIGS 薄膜光伏电池超越方程中的未知参量和CIGS 薄膜光伏电池I-V曲线的数值求解;
3)研究了2 条二阶Bezier 曲线最优控制点位置与CIGS 薄膜光伏电池填充因子之间的函数关系,提出了一种CIGS 薄膜光伏电池I-V曲线拟合方法,该方法简单准确且无需迭代等复杂数值计算,仅需厂商数据手册提供的开路电压、短路电流和最大功率点数据即可进行拟合。
附录见本刊网络版(http://www.epae.cn)。
