计及市场化电价信号导向的含高比例水电输电网扩展规划

王富阳，刘友波，胥威汀，苟 竞，刘 方，苏韵掣，刘俊勇

（1. 四川大学 电气工程学院，四川 成都 610065；2. 国网四川省电力公司经济技术研究院，四川 成都 610041）

0 引言

随着电力体制的进一步改革，电力市场化程度不断提高［1］，传统电力规划缺乏市场经济与电价导向的价值内涵，难以反映未来一段时期竞争市场模式下全局供需态势对电网投资收益、市场主体意愿和社会效益的量化影响。在电力市场交易中，水电凭借较低的边际成本，价格竞争优势明显，但由于其受地理位置限制，电源点往往远离负荷中心，导致外送通道断面阻塞，局部窝电现象严重。因此需通过电网输电线路扩展规划疏导水电外送阻塞断面，促进水电资源消纳，推动资源优势转化为经济优势。在放松管制的市场环境下，电网企业盈利模式发生转变，双边交易与集中式交易合约能否完成交割直接影响企业效益，若能通过电网扩展规划带动区域负荷增长以及促进清洁能源消纳，则不仅可降低社会用电成本，而且可提升系统过网利用效率，实现电网企业利益与社会利益激励相容。

传统电网扩展规划很少计及市场交易的价格出清信号影响，而多从运行方式、安全标准等角度提高电网的传输能力与稳定性以满足负荷需求［2］。在新一轮电改下，输配电环节被列为重要公共事业，电网作为垄断资源，输配电价由政府按照固定投资回报率的形式核定。根据经济学中的阿弗奇-约翰逊效应［3］，固定投资回报率模式易导致企业的过度投资倾向，浪费社会资源。因此，如何顺应电力市场化改革趋势，以市场化交易信号为导向，激励电网企业优化资源配置是亟待解决的问题。

电力市场环境下的输电网扩展规划研究主要考虑网络阻塞与输电投资，现有相关研究主要通过量化网络阻塞程度来评估不同规划方案对阻塞的疏导效果［2］，或分析输电阻塞对市场环境下电网扩展规划投资的激励作用［4］。文献［5］提出一种双边市场下以社会福利最大化为目标的输电网扩展规划方法，但是扩展规划结果与发用电双方的市场行为相互影响，该研究缺乏对市场主体意愿的考察。文献［6］根据输电网扩展规划模型，进行不确定性风电与负荷联合场景下的输电线路选址定容，该模型计及新能源接入对电网扩展规划决策的影响，使用k-means聚类计算典型源荷运行场景，对比不同场景下规划结果的差异。在高比例清洁能源接入下，由于清洁能源的市场行为及其波动性给电网带来运行方式的差异［7］，规划时需要全面考虑不同运行方式下的投资综合收益［8］。不同于风电在时空分布上存在的高不确定性，水电的主要问题在于电源地理位置偏远、丰枯出力差异巨大，导致丰水期水电聚集区域窝电现象严重，因此需根据其丰枯特性分析不同运行方式下电网扩展规划投资效益。针对电网规划所存在的过度投资倾向，文献［9］提出激励相容的输电成本有效性电网扩展规划模型，基于有效输电成本而非投资总成本对电网的投资收益率进行核算，该投资模型从成本核算角度引导资源优化配置。以市场信号为导向、以价值为激励引导电网投资行为是放松管制的市场模式下扩展规划研究的新思路。

本文提出计及市场电价信号导向的含高比例水电输电系统扩展规划模型，旨在以市场化电价信号引导扩展规划决策，促进水电资源消纳，从而降低社会用电成本，提高系统过网利用效率。上层规划决策模型计及电网企业作为投资主体的投资意愿，最大化规划投资收益，形成决策线路；下层市场出清模型以社会总发电成本最小为目标，采用改进的k-means 聚类算法根据水电出力以及负荷波动生成电网年运行典型日，并按其运行方式在规划后的网络进行市场交易出清，基于单时段用户响应模型量化线路规划后所能撬动的负荷增量，进而改进上层投资决策。该模型基于高比例水电网络潮流特点与水电的市场交易特性，以市场化的价格信号为导向进行电网扩展规划，同时以投资收益最大化激励电网的投资行为，促进含高比例水电输电系统的水电资源消纳。

1 计及市场化电价信号导向的含高比例水电输电系统扩展规划模型

目前我国水电发展迅速，在水资源丰富的地区，不同电压等级电网均有不同规模水电电源点接入，而目前的研究中还没有对含高比例水电输电系统概念的公认标准。含高比例水电输电系统由于水电外送断面压力显著，其丰枯特性导致不同季节节点边际电价差异巨大，可能会给市场交易主体以及电网的运行调度带来风险与困难。因此，本文主要研究水电聚集态势下，电网的市场交易信号特征及其对电网扩展规划决策的影响，为使模型达到实际规划应用效果，结合我国西南地区实际运行情况，本文定义丰水期水电占比达到70%的输电系统为含高比例水电输电系统。

阻塞反映出电网传输能力与源荷传输需求的不匹配，同时线路阻塞也会导致电力市场出清过程中节点边际电价出现阻塞分量。因此，可以将阻塞以市场交易信号即节点边际电价的形式向电网传递未来一段时间的规划需求与方向。

1.1 节点边际电价与阻塞盈余

市场化电价信号主要指市场出清过程所得到的节点边际电价，其反映了节点提升单位负荷所需的社会边际发电成本。本文使用直流最优潮流模型求解系统节点边际电价。直流潮流模型的基本形式为：

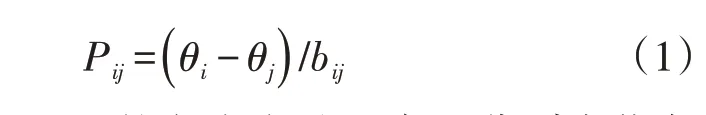
式中：Pij为线路i-j上的潮流流量；θi与θj分别为节点i与节点j的电压相角；bij为线路i-j导纳。

式（1）的矩阵形式为：

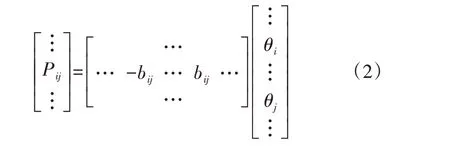
该矩阵展开式可简化写成Pz=Kθ。其中，Pz为线路潮流矩阵；K为式（2）中包含支路导纳信息的矩阵；θ为节点电压相角矩阵。

令T=KB-1，得到节点注入功率与相角有如下关系：

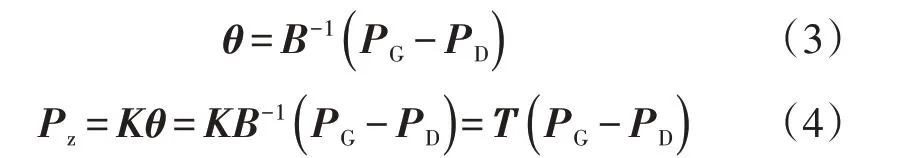
式中：B为节点导纳矩阵；PD为负荷参数矩阵；PG为发电机出力矩阵。根据直流潮流方程，可得到通用的直流最优潮流模型。本文市场交易模式采用集中交易模式，市场的报价采用单边报价，由电源侧上报报价曲线，用户作为价格的接收者［10］。具体出清模型的矩阵形式如下：

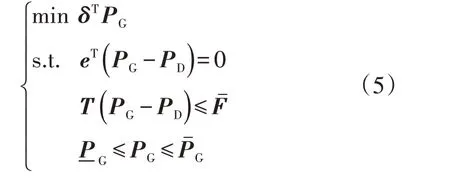
式中：μriTri为阻塞成本分量。线路阻塞导致系统中边际成本机组无法被调用，造成社会总用电成本的提高。对于含高比例水电网络，丰枯水季网络潮流差异显著，水电的低成本、丰枯差异明显、地理位置远离负荷中心等特点导致原有电网的阻塞问题愈加严重。当不同节点的节点边际电价存在差异时，不同节点之间的电力交易分别按照所在节点边际电价进行出清，这使得电力交易出现由阻塞所导致的交易盈余，将这种负面市场信号定义为阻塞盈余。

阻塞盈余Cs以下述形式量化网络阻塞的程度：

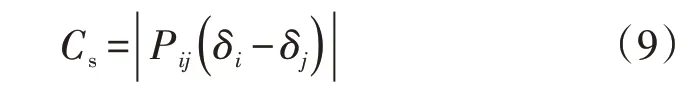
当全局电价差异较小时，阻塞盈余会相应减小。阻塞盈余反映了社会用电成本的浪费，因此在电力市场环境下分析电网规划决策时，经常将阻塞盈余作为阻塞分析的经济效益指标。

1.2 负荷价格弹性

需求价格弹性是指市场商品需求量对价格变动做出反应的敏感程度。负荷价格弹性反映负荷对于电价变化的敏感程度，量化电价差异对负荷的影响，体现了负荷侧对于电网扩展规划结果的满意程度。通过引入市场化电价信号后的区域负荷响应特征，量化线路规划后所能推动的负荷增量，可提升系统过网利用效率。本文主要分析规划后负荷的近似饱和状态，某一时段内负荷的平移以及不同地理位置之间负荷的相互替代对于电网长期运行中的负荷总量没有影响，因此本文只考虑功率可变负荷的自弹性，不考虑可平移负荷以及可中断负荷所带来的交叉价格弹性，故采用单时段节点用户响应模型。假设电价对负荷大小的影响为：

式中：Q′为响应后的负荷需求量；Q0为响应前的负荷需求量。假设用户的效益与用电量的函数为B(Q′)，则用户的收益E为：

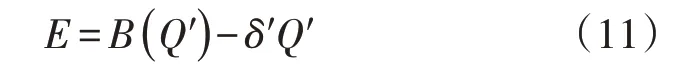
式中：δ′为响应后的节点边际电价。

为求得用户收益的最大值，则有：

在实际运行中，不同节点的负荷价格弹性受到地理位置、政策导向等多方面因素影响，这些影响难以通过精确的数学表达式表示，因此可采用模糊推理法［12］计算不同节点需求价格弹性系数。

1.3 计及市场化电价信号导向的输电网扩展规划模型

本文中计及市场化电价信号的输电网扩展规划模型采用双层规划模型。上层为规划层，对规划投资预算采用等年值法根据规划年限计算投资成本的净现值，相较于传统扩展规划模型中对单条线路是否投入的决策，该模型更加强调线路的投资组合收益，从多条待选线路中决策出最佳的线路投资组合。下层为出清层，采用改进k-means聚类得到含高比例水电网络全年典型运行方式，在不同运行方式下依托上层线路投资组合对市场交易进行出清，模拟市场化运行条件下以电价为引导的功率传输与外送以及水电消纳态势。新建的线路可以缓解功率传输阻塞，相应减少节点边际电价中的阻塞分量，进而通过价格的疏导来激励负荷增长，并通过引入区域负荷价格响应特征，量化规划带动的负荷增量，改进规划层决策。上、下层模型的逻辑关系如图1所示。

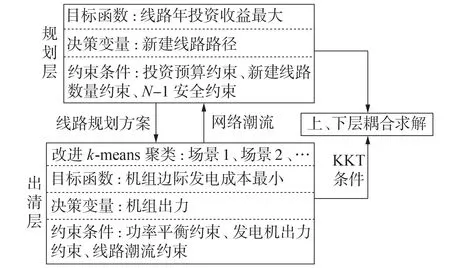
图1 上、下层模型的逻辑关系图Fig.1 Logic relationship diagram between upper and lower layer models

1.3.1 规划层模型

规划层模型以线路年投资收益Pro最大为目标，投资成本考虑施工材料成本、人工成本等，不同成本按照每千米进行统一折算，输配电价按照区域统一价格计算。目标函数表达式为：

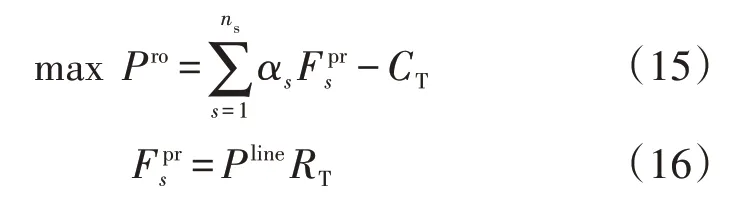
上层模型约束考虑线路投资的投资预算约束、新建线路数量约束以及N-1安全约束。

1）投资预算约束。

投资预算资金采用等年值法根据投资年限计算年等值投资成本，其表达式为：

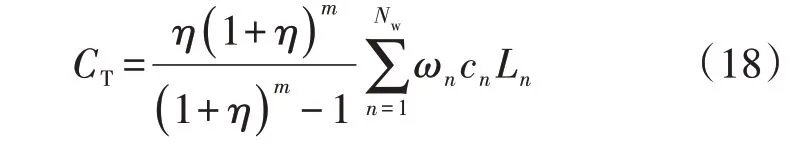
式中：η为贴现率；m为规划年限；ωn为待规划线路n的决策变量，其值为1 表示新建，为0 表示不新建；cn和Ln分别为线路n单位长度投资成本和总长度；Nw为待选集中线路数量。

线路的投资成本约束为：

式中：Cmax为投资预算最大值。

2）新建线路数量约束。

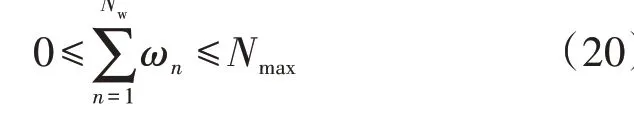
式中：Nmax为输电线路新建数量最大值。

3）N-1安全约束。

考虑到双层模型的求解与N-1安全校核同时进行会导致模型求解困难，本文采用规划决策与N-1安全校核分开进行的方式，在求解完上、下层规划决策后再进行新网络的N-1安全校核。如果N-1安全校核通过，则形成最终的扩展规划决策；否则，对上层模型添加最大利润约束，排除该不满足安全约束的扩展规划决策，进行新一轮的优化求解。

1.3.2 出清层模型

出清层模型即为前文所述的直流最优潮流模型，考虑不同运行方式下的出清情况，单一典型日运行方式下的出清模型如下。

目标函数为：

本文假设电力供应商在市场中的报价行为均是理性的，即以机组的边际发电成本报价。火电机组的发电机成本曲线可以用二次曲线表示，为了计算方便，以分段成本曲线代替二次曲线。水电机组的边际成本较小，近似以线性报价曲线来表示［13］。

约束条件考虑系统功率平衡约束、线路潮流约束以及发电机出力约束，分别如式（22）—（24）所示。

2 典型日选取与模型求解

2.1 典型日选取

典型日的选取是对电网长期时序变化场景的简化。负荷在不同时段不断变化，但其在固定时间周期内的变化趋势符合一种长期的规律［13］。同样，水电机组出力在一年中随着季节气候的变化呈规律性波动。在实际系统运行中，往往按照季节与负荷大小人为对全年运行方式进行划分，该方法能够较快速地解决大多实际规划运行问题，但由于缺乏科学理论依据，规划结果可能与预期存在较大偏差。因此，本文选取改进的k-means聚类算法对含高比例水电电网全年的运行方式进行聚类计算［13］，产生典型场景集。聚类样本的选择应充分覆盖整个运行周期，涵盖丰枯水季负荷大小方式运行下的各种场景［14］，并且所选择的聚类样本数据容量越大，聚类效果越贴近规划实际［15］。相较于传统k-means 聚类算法，改进k-means 聚类算法可以在聚类数范围内，通过比较CH（Calinski-Harabasz）有效性指标［16］，确定最优聚类数［17］，在聚类数取值范围［18］内比较不同聚类数下结果的CH指标。CH指标的定义如下：

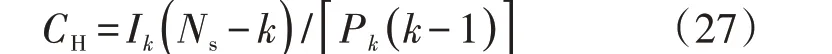
式中：CH为CH 指标值；Ik、Pk分别为聚类数k下类间与类内离差平方和；Ns为样本总数。寻找最优的聚类数，相当于寻找CH的最大值。算法的计算步骤如附录A图A1所示。

2.2 上、下层模型耦合

为了避免传统启发式算法的求解不稳定性［19］，对下层模型列写其KKT 条件，将双层优化模型转化为单层优化模型进行稳定求解［20］。模型的目标函数为式（15），上层模型的约束条件为式（18）—（20），下层模型的约束条件为式（22）—（26）。由于约束的矩阵形式表达式便于列写其KKT 条件，因此这里以矩阵形式列写下层约束的等效约束条件：

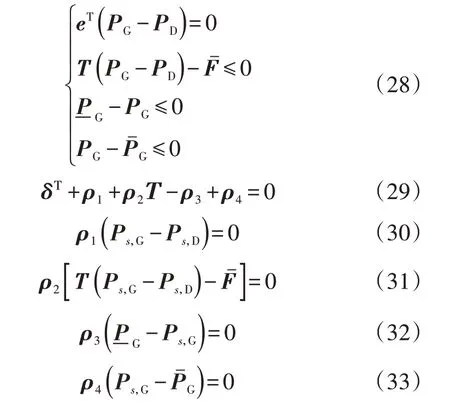
式中：ρ1—ρ4为等式约束与不等式约束的拉格朗日乘子向量；Ps，G、Ps，D分别为运行方式s下节点的发电机出力矩阵与负荷矩阵。式（29）—（33）为下层利用KKT条件引入的新的约束条件。

KKT条件将下层优化问题转化为一组等式约束条件并入上层，实现了上、下层模型的耦合，将双层规划问题转化为单层混合整数规划问题，该问题可调用成熟的商业求解器进行稳定求解。

3 算例计算

3.1 算例数据

本文算例采用修改的我国西部某区域实际电网，网络拓扑如附录A 图A2 所示。该网络共有91个节点，其中负荷节点63个，电源节点28个，包括火电站7 座，水电站21 座。水电站具有集中分布的特点，且与负荷集中区域地理距离较远，在丰水期具有显著的水电外送困难问题。

从规划年365 d的节点负荷、水电出力数据中选取各数据的最大值，并且按照比例对不同节点的负荷以及发电机出力进行折算，化归为0～1 之间的数据。采用改进的k-means 聚类算法计算得到最优聚类数为4。按照负荷以及水电机组出力的大小（丰枯水期）将全年运行方式聚类为4 种典型运行方式，可分别描述为丰水期负荷大方式运行（丰大）、丰水期负荷小方式运行（丰小）、枯水期负荷大方式运行（枯大）以及枯水期负荷小方式运行（枯小）。最终聚类出的4种典型运行方式的划归数据如附录A图A3所示。4 种典型运行方式在全年的时间占比均为25%，即：

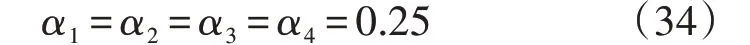
由于该实际网络为高电压等级输电网络，因此其中电源节点并非表示单一电站或机组，而是表示该节点挂接的所有机组的总和。不同节点按照主要挂接的机组种类分为水电节点与火电节点。所有节点出力与成本的对应数据见附录A 表A1、A2，水电按照线性成本函数报价，火电按照分段成本函数报价。

通过对该实际网络规划前典型日下的潮流分析可知，在水电聚集区域（如节点71—73等）丰水期水电利用率较低，因此将待选集设置在水电聚集区域的外送断面上，并综合考虑负荷大小及扩展规划距离问题，初步确定扩展规划的待选集为｛线路70-25，线路71-25，线路73-30，线路42-82，线路52-88，线路61-86，线路77-35｝（见附录A 中图A2 的虚线线路）。待选线路参数如表1所示。

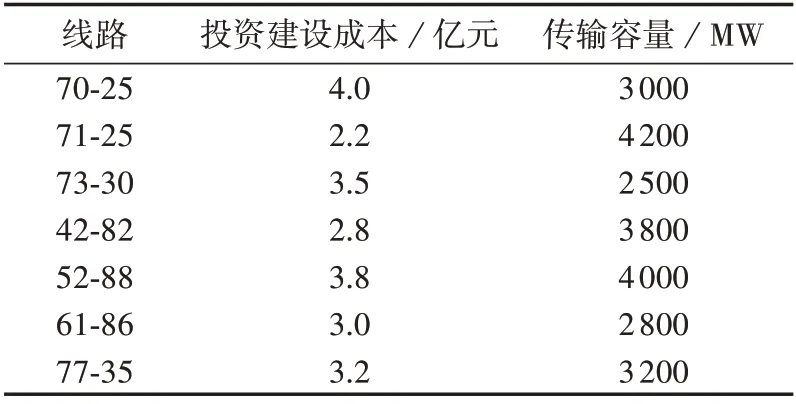
表1 待选线路参数Table 1 Parameters of lines to be selected

系统在丰大运行方式下的节点边际电价如图2所示，规划前全部4 种运行方式下的节点边际电价如附录A 图A4所示。丰水期水电资源丰富，节点大多按照边际成本最小的水电机组出清，这表明丰水期全局仍有大量水电有待消纳，节点之间的边际价格差异部分来源于不同水电机组边际成本的差异，同时水电外送通道容量不足导致部分节点只能就近消纳更高成本的火电机组；枯水期火电代替水电成为主要供电能源，除在枯小方式下少数没有被完全消纳的水电机组可以增加出力外，边际出清价格大多为火电机组边际成本，导致高比例水电系统丰枯节点边际电价差异巨大。因此，在规划时考虑实际运行中多种典型运行方式下的投资综合收益是极其必要的。扩展规划的整体目标在于打通水电通道，疏导系统节点边际电价，从而提升电价变化下的负荷增量，达到促进水电消纳、提高过网利用效率的目标。

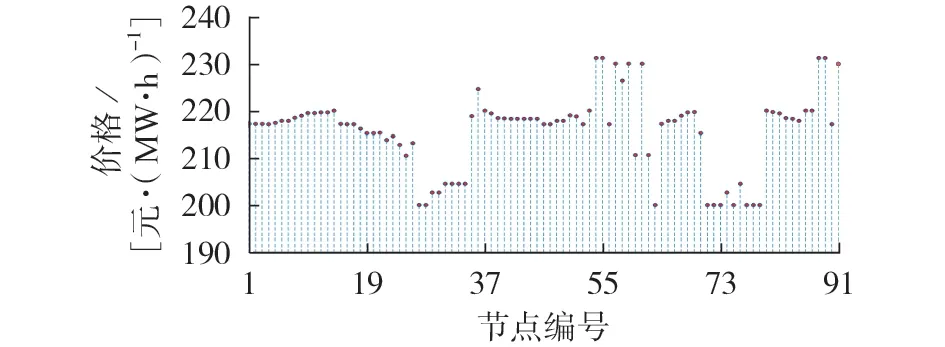
图2 丰大运行方式下系统节点边际电价Fig.2 Locational marginal price in wet season with high load

3.2 结果分析

为了对比不同规划方法的扩展规划效果，研究市场价格信号与负荷价格弹性对扩展规划结果的影响，本文分别采用3 种规划方案对上述系统进行扩展规划：case Ⅰ，考虑市场信号及负荷价格弹性的扩展规划，即本文提出的双层规划模型；case Ⅱ，省略式（24）、（25）的负荷弹性变化过程，直接将规划后的线路潮流返回上层，即考虑市场信号但不计及负荷弹性的扩展规划模型；case Ⅲ，基于直流潮流模型，考虑运行安全标准［21］但不考虑市场信号及负荷弹性的传统扩展规划模型。负荷价格弹性系数取一般工业负荷价格弹性系数ε=-0.6。3种规划方案的结果如表2所示。

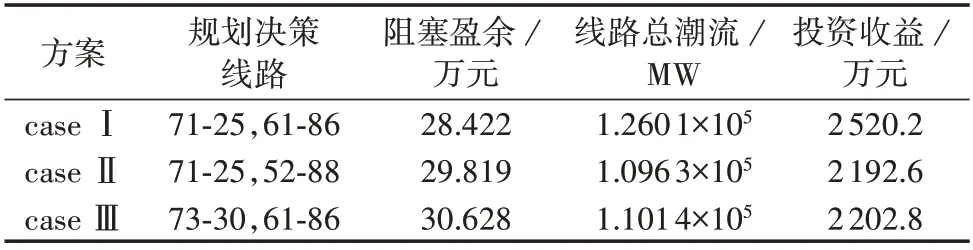
表2 3种规划方案的结果比较Table 2 Comparison of results among three planning schemes

为了更加清晰地比较3 种规划方案对系统节点边际电价的影响，图3给出了3种方案规划前后的节点边际电价曲线。

根据上述最优规划结果，规划后丰大运行方式下的节点边际电价如图4 所示。全部4 种运行方式下的节点边际电价见附录A图A5。

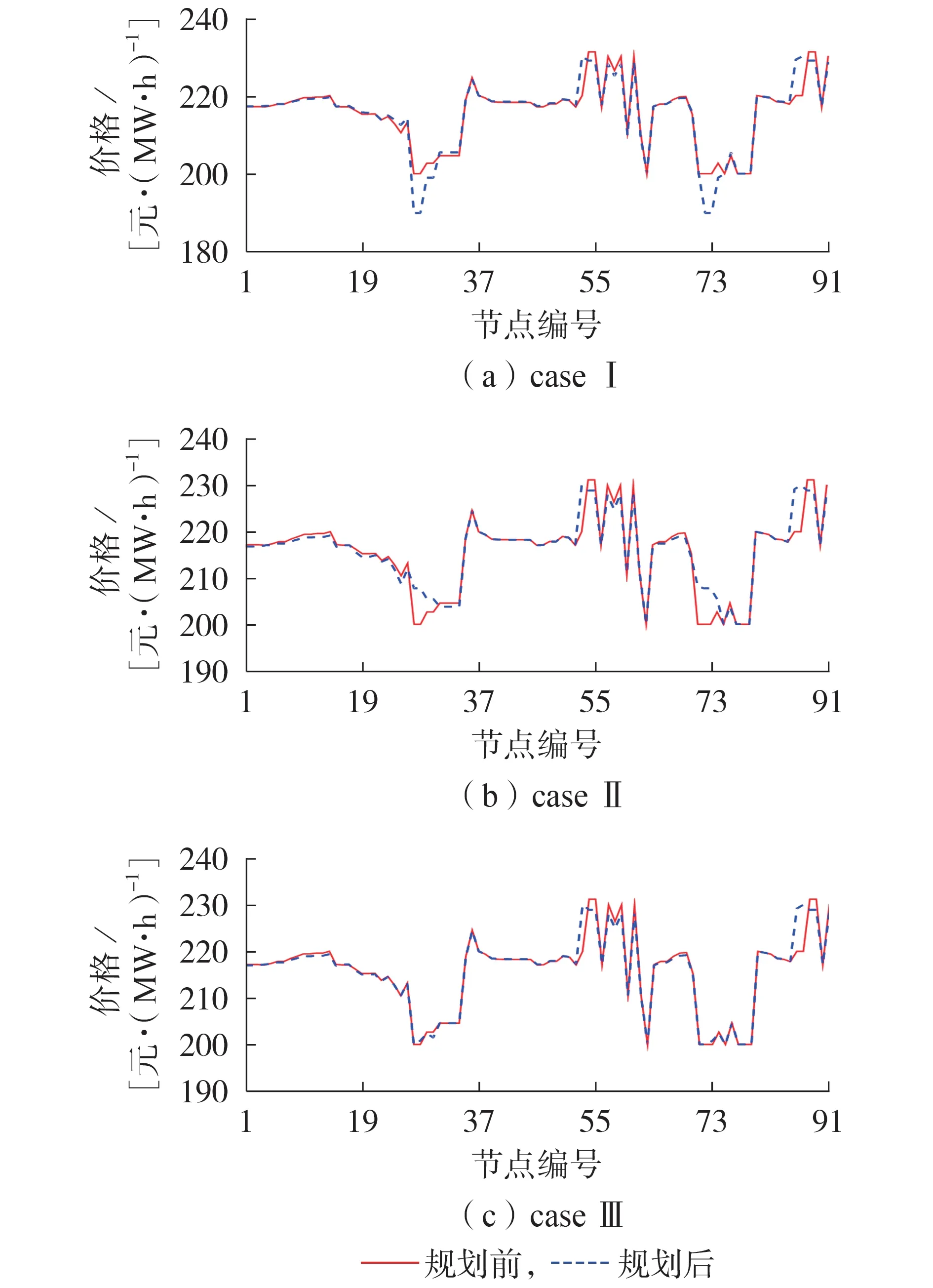
图3 3种规划方案下的节点边际电价对比Fig.3 Comparison of locational marginal price among three planning schemes

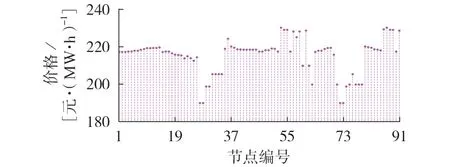
图4 规划后丰大运行方式下节点边际电价Fig.4 Locational marginal price in wet season with high load after planning

与规划前相比，除节点边际电价有明显下降趋势外，电价的区域波动性更小，不同节点边际电价趋于统一，即系统阻塞盈余减少。其中，在枯大方式下，由于负荷小方式运行，电源供电压力较小，规划后网络几乎无阻塞，系统基本按照统一边际电价出清。

从图3 规划前后节点边际电价的对比图可见，case Ⅰ的规划效果最优，节点27 的电价下降10.83元／（MW·h），节点73的电价下降9.92元／（MW·h），降幅达到5%，而case Ⅱ和case Ⅲ只在局部略微降低了节点边际电价，电价下降的原因在于规划前低价水电由于外送通道阻塞无法完全被消纳，扩展规划打通了水电通道，从而疏导全局电价，降低了社会总用电成本。比较表2 中不同方案的规划决策线路可知，case Ⅰ与case Ⅱ的规划决策线路均包含线路71-25，case Ⅰ与case Ⅲ则均包含线路61-86，而节点27、73 正处于case Ⅰ下节点边际电价下降最显著的区域，可见不同规划方案对电网阻塞断面都有一定的定位作用，均可以在一定程度上缓解断面阻塞问题。

但case Ⅱ由于缺乏价格弹性响应所带来的对负荷增量的考察，对阻塞盈余的疏导效果受限。同样case Ⅲ由于缺乏电价信号导向，仅以投资成本最小形成扩展规划决策，规划视角片面，对系统阻塞的定位与疏导能力有限。case Ⅱ电价仅在节点25、31分别降低了1.63、0.91 元／（MW·h），case Ⅲ电价仅在节点30下降了1.06元／（MW·h）。

阻塞盈余方面，盈余大小与相连节点边际电价差以及线路流量有关，case Ⅰ相比case Ⅱ阻塞盈余低0.139 7 万元，相比case Ⅲ降低0.220 6 万元。根据表2 中的线路总潮流可以看出，在不考虑负荷价格弹性的情况下，计及市场价格信号可以有效降低阻塞盈余，但在不撬动负荷增量的情况下，其是从降低网络通道流量的方向降低交易盈余，即促使负荷优先调用近距离低成本电源满足需求，这种规划方案忽略了电网自身的投资收益，以降低线路潮流为代价限制阻塞盈余。而计及负荷价格弹性时，在通道利用率增大的同时系统阻塞盈余减小，即该规划方案刺激了电价差均一地区不同节点的功率交换，而减少节点边际电价差明显线路的功率传输，从价格降低与流量增加2 个角度限制规划决策，从而得到投资收益最大与社会用电成本最小的最优决策。

另一方面，水电的跨区域消纳以及节点边际电价的下降提升了弹性负荷需求，需求增量带动过网潮流增加，从而提高了电网投资收益。规划后丰大方式下，由负荷价格弹性响应，系统总增负荷需求提高406.1 MW，水电增发出力3 689 MW，系统总过网潮流提高2 947 MW。需求价格弹性放大了市场化电价信号对扩展规划的量化影响，反映出市场需求侧交易主体的扩展规划意愿。

网络阻塞导致全局用电成本的提高，类比节点边际电价的定义，线路减少单位传输容量所导致增加的用电成本即为总用电成本关于线路容量的灵敏度。而不同规划方案对阻塞断面定位效果不同，由前文可知，相比传统规划模型方案，本文方案效果更好。因此可从节点边际电价的计算机理出发分析本文所提方法对阻塞定位的能力。类比其求解思路，同样可以求解KKT 等式中总用电成本对线路容量的灵敏度，即线路约束拉格朗日乘子。

图5 为规划前后线路容量约束对应的拉格朗日乘子对比图。拉格朗日乘子大小表示线路减少单位传输容量后系统总的发电成本增量，即提高的社会总用电成本，其值为0表示线路不存在阻塞。由图5可以看出，线路28（即线路25-27）和线路86（即线路77-36）的拉格朗日乘子明显下降。而求解得到的规划决策线路正是位于阻塞线路所在区域，这表明实际运行中的网络阻塞程度与模型中线路约束拉格朗日乘子相对应，通过以用电成本最小为目标求解最优潮流，可以对网络阻塞断面进行预先定位，从而优化扩展规划待选集的选取。规划后线路66（即线路60-62）的拉格朗日乘子有所提升，其原因在于系统阻塞缓解带来节点边际电价的下降，本文模型考虑了节点边际电价下降对负荷的激励作用，因此，负荷的增长会给原有线路的传输带来更大的压力，有限的投资预算无法缓解每条线路的传输压力，这也从侧面反映了考虑负荷价格弹性的必要性。

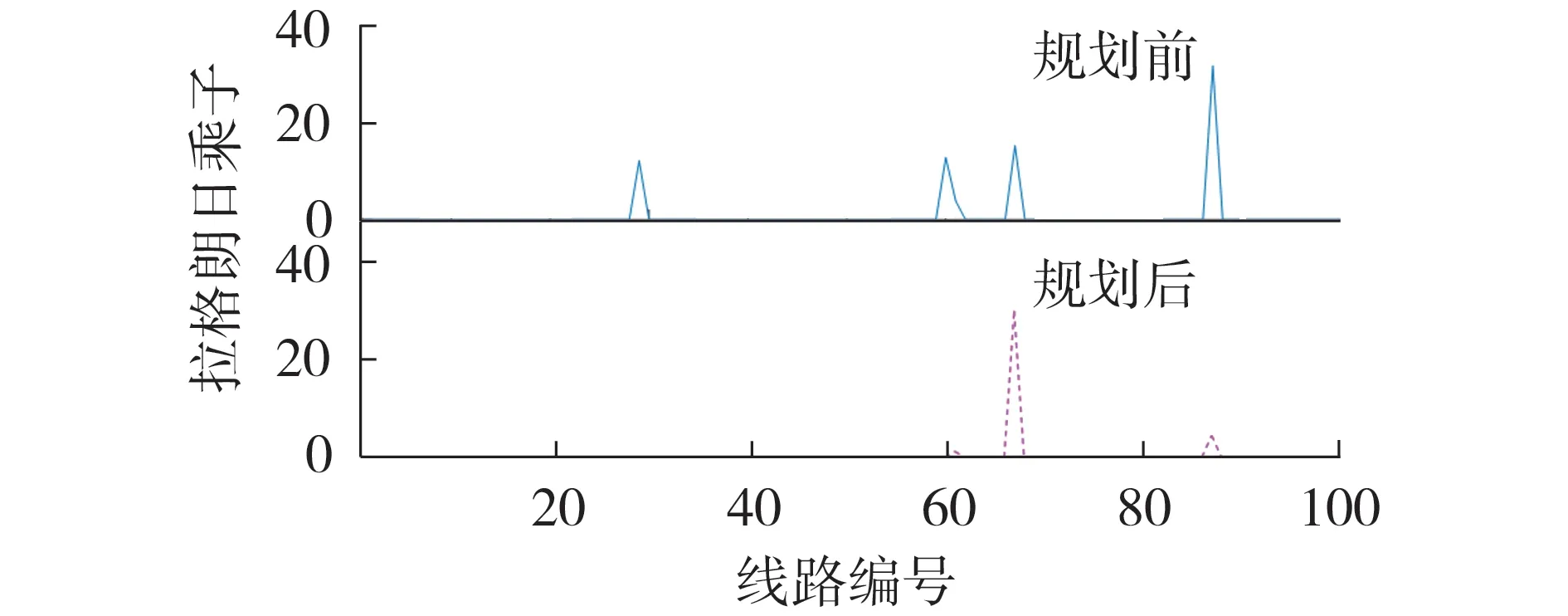
图5 规划前后线路容量约束对应的拉格朗日乘子对比Fig.5 Comparison of Lagrange multiplier corresponding to line capacity constraints between before and after planning

全局水电消纳比例是衡量区域水电消纳水平的重要参数，表3给出了4种运行方式下扩展规划前后区域内的水、火电出力。

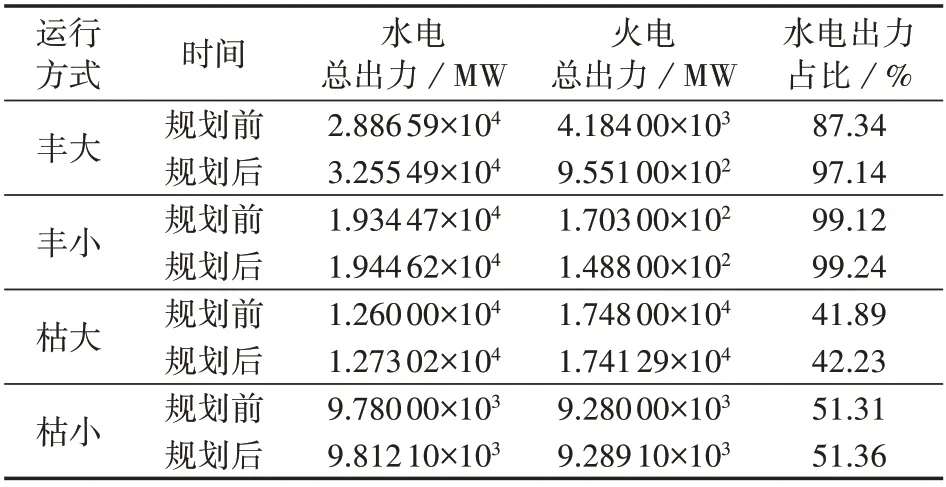
表3 4种运行方式下的水、火电出力Table 3 Hydro and thermal power output under four operation modes

在枯水期水电资源短缺，外送通道压力小，仅有的水电可以轻松地被市场消纳，因此弃水问题多发生在丰水期。丰小方式下负荷远小于网络传输上限，阻塞问题并不突出，规划前后水电消纳变化较小，而丰大方式下，水电的消纳问题最为突出。从表3可以看出，规划后丰小、枯大、枯小3种方式下水电出力占比稍微提高，而丰大方式下水电出力占比提高了9.8%，可见规划决策明显提高了丰水期水电外送通道的传输能力，在负荷大方式下尽可能多地调用水电资源满足负荷需求，从而减少了丰水期弃水。

4 结论

在电力市场化改革深入推进的背景下，本文将市场化交易信号纳入电网扩展规划研究，以高比例水电输电网络作为载体，提出计及电价信号导向的高比例水电输电网扩展规划模型。与传统扩展规划相比，本文提出的规划方法以市场交易信号为导向，计及节点负荷价格弹性，可以有效缓解网络阻塞，在促进水电资源消纳的同时撬动负荷需求增长。

实际含高比例水电输电系统的算例分析表明，所提出的扩展规划模型提高了电网投资收益，降低了社会用电成本，实现了社会福利最大化。同时，通过对网络阻塞盈余等交易信号的分析，该模型可以对阻塞断面进行定位，并评估不同线路阻塞对社会用电成本的量化影响。后续将进一步深化对实际输电网扩展规划问题数学模型本质的研究，结合更多实际算例开展模型应用。

附录见本刊网络版（http：//www.epae.cn）。