基于反演滑模控制的叉车式AGV 路径跟踪

2021-11-20向中凡刘建新王玉超

西华大学学报（自然科学版） 2021年6期

李航，向中凡，刘建新，王玉超，王强

（西华大学机械工程学院，四川成都 610039）

自动导引车（automated guided vehicles，AGV），又名无人搬运车，是一种自动化的无人驾驶的智能化搬运设备，能够沿着规划的路径进行跟踪前进，属于移动式机器人系统[1]。自动导引车（AGV）在智能搬运系统中起着核心作用[2]。随着物流仓储行业及制造行业的不断发展，智能化、低成本化、高效率化、高集成化成为了叉车行业发展的方向，随着机器人技术的发展和对先进搬运系统需求的增长，自动引导车的应用逐渐普及[3-4]。

如何保证叉车式AGV 的路径跟踪精度，是叉车式AGV 实现工程应用必须解决的问题。文献[5]提出了一种反正切函数改进指数趋近律的方法，解决了趋近律无法趋近于原点的问题，保证了在滑模面附近滑动，但是存在参数选择不确定性，跟踪精度不高的问题；文献[6]提出了双幂次趋近律的控制方法，解决了收敛速度的问题，但在外界干扰下运动稳定性和精度都会下降。文献[7]提出了一种多幂次趋近律的滑模控制方法，解决了抖振现象、收敛速度较慢及动态响应不平滑等问题，但也存在平衡点动态不稳定以及对于多幂次的系数难以确定的问题。文献[8]将组合趋近律的反演滑模控制算法应用于差速驱动的AGV，取得了较好的跟踪效果。文献[9]将模糊控制算法应用于单舵轮AGV 的路径跟踪，减少了振动幅度，但是未能实验验证。文献[10]将自适应的反演滑模控制算法应用于全向AGV，从理论分析的角度看，其在减弱抖动方面有效，但是在实际的测试过程中其自适应参数的选择和调试所需的工作量较大。从公开发表的文献来看，滑模控制算法在单舵轮叉车式AGV路径跟踪及抖振控制方面的应用研究很少。本文针对叉车式AGV 的路径跟踪以及抖动控制的问题进行研究，提出了一种适用于叉车式AGV 的由幂次趋近律和反正弦函数构成的滑模控制方法。

1 叉车式AGV 运动学模型

叉车式AGV 的底盘结构主要有五轮式和三轮式。三轮式叉车AGV 的承重能力、灵活性和稳定性都较差。五轮式叉车AGV 相较于三轮式，在舵轮左右两侧各增加1 个万向轮，提升了稳定性，能辅助转向，其综合性能优于三轮式[11]。本文假设叉车式AGV 在运动过程中不考虑车轮的侧向滑动以及侧向力，故该叉车式AGV 的车辆模型示意图如图1 所示。

图1 叉车式AGV 模型示意图

将图1 所示模型转换为基于阿克曼的转向原理的车辆运动学模型，如图2 所示。

图2 叉车式AGV 运动学模型

图2 中：XOY为全局坐标系；xAy为局部坐标系；叉车式AGV 从动轮轴线的中心为局部坐标系的原点；L为叉车的轴线距离；W为叉车从动轮的中心距离；θ为局部坐标系与全局坐标系的夹角；δ为主舵轮与局部坐标xAy中x轴的夹角；O′为叉车式AGV 转弯半径的中心；R为转弯半径；叉车式AGV 的中心参考点是叉齿的2 个从动轮的中心轴线的中点，即A(xa,ya)；主舵轮的中点在全局坐标系中的坐标为B(xb,yb)；v为主舵轮的速度；ω为叉车式AGV 的转向角速度。

原型系统通过NAV350 激光雷达导航传感器来进行定位，并获得激光雷达传感器在全局系中的坐标点C(xc,yc)。由于点A与点C不重合，因此需要进行空间坐标系的转换。以主舵轮点B为中心点，根据叉车式AGV 的运动学模型，其运动学方程为：

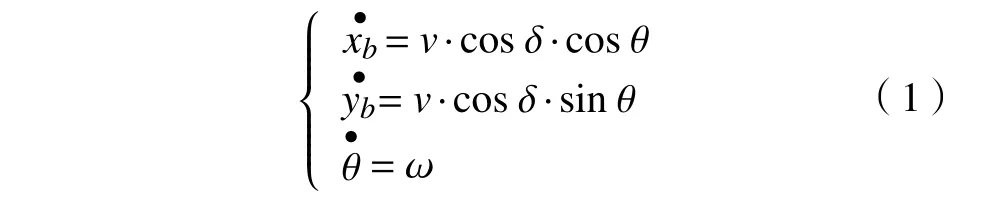
根据图2 中的运动学模型，可得

由于激光雷达传感器的安装位置和主舵轮的位置重合（忽略安装误差），所以激光传感器的扫描位置C(xc,yc)与B(xb,yb)在局部坐标系xAy中重合，即

通过式(4)的转换可以得到叉车式AGV 的坐标原点A在全局坐标的位置，为

通过对式（4）化简可得式（5），即为叉车式AGV 的参考原点在全局坐标系上的坐标点A(xa,ya)，然后再对式（5）求导，可得到式（6）。

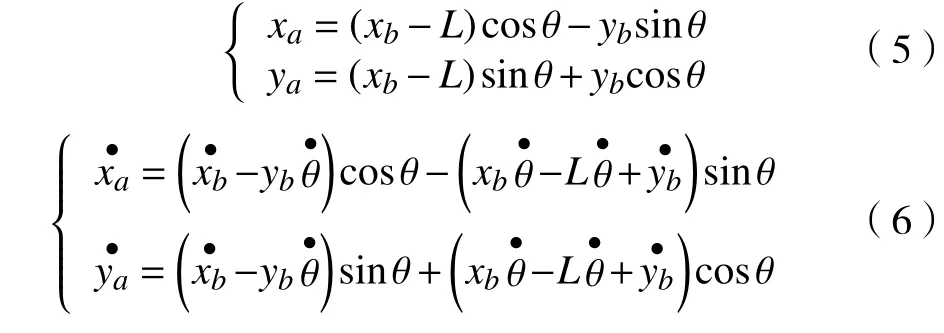
将式（1）和式（2）代入式（6），得：

以点A为原点的运动学方程表示式为

2 趋近律的设计

为了降低滑模控制的抖振，提高路径跟踪的精度，本文采用一种基于新型趋近律的滑模控制方式，即由幂次趋近律和反双曲正弦函数构成的趋近律[14—15]。

利用特殊幂次函数fal(x,α,δ)设计一种趋近律，非线性函数fal(x,α,δ)为

式（10）中，0 ＜δ＜1，α＞ 0，δ为fal(x,α,δ)在原点附近正负对称线性段的区间长度。并且fal(x,α,δ)为非连续函数，当求其一阶导数时，可按x的取值区间分段计算。本文提出的新型趋近律的表达式为

其中s为滑模函数,ε ＞ 0，k＞ 0,arsh(s) 为反双曲正弦函数。

将式（10）和式（12）代入式（11）可得式（13）。

3 反演滑模控制器的设计

反演滑模控制器是将叉车式AGV 的当前姿态p(x,y,θ)与期望位姿pr(xr,yr,θr)的误差作为控制器的数据输入，控制即对速度v和转向角δ进行控制。为控制器设计方便，令控制输入(u1,u2)可以表示为(δ,v)，该控制量是对叉车式AGV的单舵轮进行控制跟踪的主要参数，所以该控制器的主要控制方式是首先计算出叉车式AGV 的速度和角速度，然后根据数学模型计算出对叉车式AGV 的单舵轮进行控制的控制量即为(u1,u2)，从而实现路径跟踪的目标[16]。

为了实现叉车式AGV 的路径跟踪控制，本文采用基于新型趋近律的滑模控制方法，并结合叉车式AGV 的运动学模型，得出叉车式AGV 的路径跟踪控制结构框图，如图3 所示。

图3 控制结构图

首先设计该模型的滑模面切换函数。由于是对叉车式AGV 的位姿进行控制，所以需要分别设计滑模面切换函数。根据反演法，滑模面的切换函数如式(14)所示，由横向位移误差、纵向位移误差进行滑模面[17]设计得到。由此可得趋近律如式(15)所示。其中i=1,2,3。

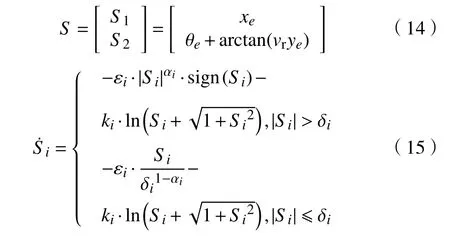
通过滑模控制器计算后的误差状态方程可以解得横向、纵向以及姿态角的误差值，即

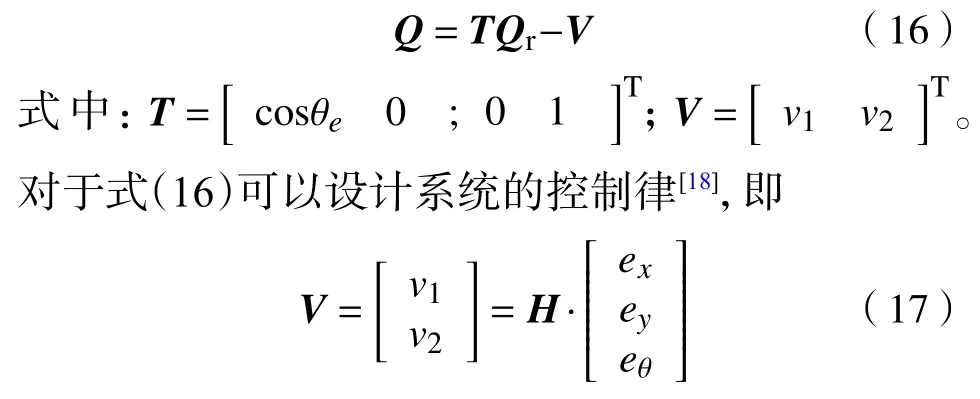
其中增益矩阵H为

将式（17）和式（18）代入式（16），可得

给出期望的叉车式AGV 的运行速度和角速度，将其代入式（19），可得

将计算得到u2值代入式（2），得到u1值，为

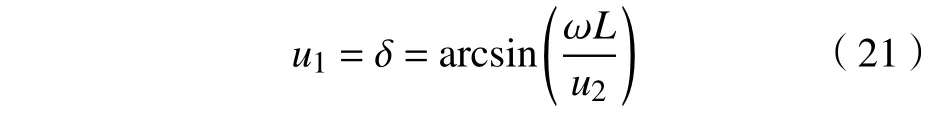
由此通过滑模控制器的计算可以得到叉车式AGV 的控制量u1、u2，最终实现对期望路径的跟踪。

4 实验验证

MATLAB 软件提供了一个动态系统建模、仿真和综合分析的集成环境[19]。利用MATLAB 软件对叉车式AGV 的运动学模型和新型趋近律的滑模控制器进行路径跟踪仿真。因为该控制器是基于新型趋近律的滑模控制，所以为了消除运行中由于符号函数引起的抖动，利用饱和函数代替符号函数[20-21]，饱和函数的表示式为

式中，参数 δ＞0，称为边界层。采用饱和函数sat(S/δ)代替符号函数后，在边界层内采用线性化反馈控制，在边界层外采用切换控制。在路径跟踪仿真实验中，由于规划的路径主要是直线和圆弧，所以跟踪实验主要是直线和圆弧跟踪路径。

4.1 仿真验证

笔者通过在MATLAB 软件中进行运动仿真，从而得出在不同趋近律的实验条件情况下，叉车式AGV的运动跟踪效果。在仿真实验中，叉车式AGV的初始位置为，期望的控制量。通过实验可以得到指数趋近律、等速趋近律、幂次趋近律、新型趋近律的跟踪效果，如图4 所示。其中：新型趋近律的跟踪响应时间更快，趋近速度更快；等速趋近律的跟踪响应速度最慢。