环中幂等元的积与差的n-强Drazin逆

魏玉洁，邹红林

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

1 引言与预备引理

设R是有单位元的结合环。N(R)表示R上所有幂零元组成的集合。令comm(a){x∈R|ax=xa}，comm2(a){x∈R|yx=xy,∀y∈comm(a)}.

为了读者的方便，我们先介绍相关概念。

定义1[8]设a∈R.若存在x∈R满足下列条件：

xax=x,ax=xa,a-a2x∈N(R)

则称x是a的Drazin逆，记为x=aD.若x存在，则它一定唯一。RD表示R中所有Drazin可逆的元素组成的集合。

定义2[1]设n∈,a∈R.若存在x∈R满足下列条件：

xax=x,ax=xa,an-ax∈N(R)

则称x是a的n-强Drazin逆，记为x=ansD.若x存在，则它一定唯一。RnsD表示R中所有n-强Drazin可逆的元素组成的集合。特别地，当n=1时，称x是a的强Drazin逆。记为x=a1sD=asD.用RsD表示R中所有强Drazin可逆的元素组成的集合。

关于n-强Drazin逆，文献[9]中有以下结论，本文直接以引理的形式给出。

引理1[9]设n∈，则a∈RnsD当且仅当a-an+1∈N(R).

引理2[9]设n∈，若a∈RnsD，则a∈RD且aD=ansD.

根据引理2和文献[8]中的定理1可知：设a∈RnsD.若ab=ba，则ansDb=bansD，即ansD∈comm2(a).

引理3 1) 设n∈，a,b∈R使得ab=0，则a,b∈RnsD⟺a+b∈RnsD.

2) 设n∈，a,b∈R使得ab=ba=0，则a,b∈RnsD⟺a+b∈RnsD.此时

(a+b)nsD=ansD+bnsD.

引理4[9]设a,b∈RnsD，且ab=ba，则ab∈RnsD且(ab)nsD=bnsDansD.

由引理2知，(ab)nsD=(ab)D，再结合文献[10]的引理2 ：(ab)D=bDaD=aDbD，所以有，

(ab)nsD=aDbD=ansDbnsD.

引理5[9]若a,b∈R，n∈，则ab∈RnsD⟺ba∈RnsD，此时，(ba)nsD=b((ab)nsD)2a.

(ap+b(1-p))nsD=ansDp+bnsD(1-P).

证明 因为p2=p，所以p∈RnsD且pnsD=p.已知ap=pa，bp=pb，由引理4得，

ap∈RnsD且(ap)nsD=ansDP，

b(1-p)∈RnsD且(b(1-p))nsD=bnsD(1-p).

因为ap·b(1-p)=b(1-p)·ap=0，结合引理3 2)得，

ap+b(1-p)∈RnsD,(ap+b(1-p))nsD=ansDp+bnsD(1-p)

引理7[9]若a,b∈R，n∈，则1-ab∈RnsD⟺1-ba∈RnsD.

2 主要结果

设p,q是环R中任意两个幂等元，这一节我们将给出(p-q)2，pq，-(pq-qp)2，(pq+qp)2，pq+qp和pq-qp有n-强Drazin逆的一些条件。

定理1 设p,q是环R中任意的两个幂等元，则下列命题彼此等价：

二是要学习和实践马克思主义关于坚守人民立场的思想。学习这一思想的现实意义在于增强“共产党人不忘初心、牢记使命的自觉担当”，明确践履“理论自信”的归宿。

1) 1-pq∈RnsD2) 1-pqp∈RnsD3)p-pqp∈RnsD4)p-pq∈RnsD，

5)p-qp∈RnsD6) 1-qp∈RnsD7) 1-qpq∈RnsD8)q-qpq∈RnsD，

9)q-qp∈RnsD10)q-pq∈RnsD.

证明 由引理7可知，1)和6)等价.这里只须证1)～5)等价。

1)⟺2) 由引理7得，1-pq=1-p(pq)∈RnsD⟺1-(pq)p=1-pqp∈RnsD.

2)⟹3) 设1-pqp∈RnsD，因为p2=p，所以p∈RnsD且pnsD=p.又因为p(1-pqp)=(1-pqp)p，根据引理4得，p-pqp∈RnsD.

3)⟹2) 假设p-pqp∈RnsD，令a=p-pqp，b=1，显然有a,b∈RnsD且ap=pa,bp=pb，结合引理6得：ap+b(1-p)=1-pqp∈RnsD.

3)⟺4) 因为p-pq=p(1-pq)，p-pqp=(1-pq)p，由引理5得，

(1-pq)p∈RnsD⟺p(1-pq)∈RnsD，即p-pqp∈RnsD⟺p-pq∈RnsD.

4)⟺5) 根据引理5可知，p-pq=p(1-q)∈RnsD⟺(1-q)p=p-qp∈RnsD.

如果将定理1中的p，q分别用(1-p),(1-q)代替，可以得到下面的结果：

推论1 设p,q是环R中任意的两个幂等元，则下列命题彼此等价：

1)p+q-pq∈RnsD2)p+(1-p)(q-qp)∈RnsD

3) (1-p)q(1-p)∈RnsD4)q-pq∈RnsD

5)q-qp∈RnsD6)p+q-qp∈RnsD

7)q+(1-q)(p-pq)∈RnsD8) (1-q)p(1-q)∈RnsD

9)p-qp∈RnsD10)p-pq∈RnsD

引理8[9]设n,k∈.若a∈RnsD，则ak∈RnsD且(ak)nsD=(ansD)k.

该引理的逆命题不一定成立，即ak∈RnsD⟹/a∈RnsD.下面举例说明：

22-(22)n+1=1-1n+1∈N(3).

但是由于

所以a=2不一定是n-强Drazin可逆的。

定理2 设p∈R，q∈R且p2=p，q2=q，则下列命题彼此等价：

1) (p-q)2∈RnsD;

2) 1-pq∈RnsD;

3)p+q-pq∈RnsD.

证明 1) ⟹ 2) 假设(p-q)2∈RnsD.令a=(p-q)2，b=1显然有a,b∈RnsD，且ap=pa，bp=pb.根据引理6得，ap+b(1-p)=1-pqp∈RnsD.再结合定理1中1)和2)可知，1-pq∈RnsD.

2) ⟺ 3) 由定理1中1)和4)知，1-pq∈RnsD⟺p-pq∈RnsD.因为(p-pq)q=0，由引理3 1)有，q∈RnsD,p-pq∈RnsD⟺p+q-pq=(p-pq)+q∈RnsD.

3) ⟹ 1) 假设a=1-pqp,b=1-(1-p)(1-q)(1-p)，显然ap=pa，bp=pb.因为

1-(1-p)(1-p)(1-q)=p+q-pq∈RnsD

所以由引理7得b∈RnsD。再由定理1 2)和推论1 1)知，a∈RnsD，注意到(p-q)2=ap+b(1-p)，根据引理6有(p-q)2∈RnsD.

注记1 如果把定理2 1)中的(p-q)2换为p-q，则有 1)⟹ 2) ⟺ 3)，但

p+q-pq∈RnsD⟹/p-q∈RnsD.

根据引理8和例1知，p-q∈RnsD⟹(p-q)2∈RnsD，但是(p-q)2∈RnsD⟹/p-q∈RnsD.

由定理2知，p+q-pq∈RnsD⟺(p-q)2∈RnsD，所以p+q-pq∈RnsD⟹/p-q∈RnsD.下面的例2也说明p+q-pq∈RnsD⟹/p-q∈RnsD.

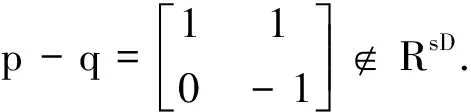
将定理2中的p用1-p代替，则有推论2.

推论2 设p，q∈R,且p2=p，q2=q，则下列命题彼此等价：

1) (1-p-q)2∈RnsD;

2) 1-q+pq∈RnsD;

3) 1-p+pq∈RnsD.

定理3 设p，q∈R,且p2=p，q2=q，则下列命题彼此等价：

1)pq∈RnsD;

2) (1-p)(1-q)∈RnsD;

3) (1-p-q)2∈RnsD.

证明 假设p′=1-p，q′=q,则q′-p′q′=pq∈RnsD，p′-p′q′=(1-p)(1-q)，p′-q′=1-p-q.下证命题1)～3)是等价的：

1) ⟺ 2) 由定理1 4)和10)知，p′-p′q′∈RnsD⟺q′-p′q′∈RnsD，所以 1)和 2)等价。

1) ⟺ 3)由定理2 1)和2)和定理1 1)和10)知，

(p′-q′)2∈RnsD⟺1-p′q′∈RnsD⟺q′-p′q′∈RnsD

即(1-p-q)2∈RnsD⟺pq∈RnsD，证毕。

定理4 设p，q∈R,且p2=p，q2=q，若pq∈RnsD，p+q∈RnsD，则(pq+qp)2∈RnsD.

证明 根据引理8可知，p+q∈RnsD⟹(p+q)2∈RnsD.根据定理3知，

pq∈RnsD⟺(1-p-q)2∈RnsD

又因为，

pq+qp=(p+q)(p+q-1)=(p+q-1)(p+1)，

再结合引理4得出，(pq+qp)2=(p+q)2(1-p-q)2=(1-p-q)2(p+q)2∈RnsD.

定理5 设p，q∈R,且p2=p，q2=q，若pq∈RnsD，p-q∈RnsD，则-(pq-qp)2∈RnsD.

证明 类似定理4的证明易知：p-q∈RnsD⟹(p-q)2∈RnsD，pq∈RnsD⟺(1-p-q)2∈RnsD.

因为pq-qp=-(p-q)(1-p-q)=(1-p-q)(p-q)，从而有

(pq-qp)2=-(p-q)2(1-p-q)2=-(1-p-q)2(p-q)2.

所以结合引理4可得，

-(pq-qp)2=(p-q)2(1-p-q)2=(1-p-q)2(p-q)2∈RnsD

注记2 定理5不能说明(pq-qp)2∈RnsD.容易证得a∈RD⟺-a∈RD，但是在n-强Drazin逆中a和-a的n-强Drazin可逆性一般没有明确的等价关系.即，在一般情况下如果a∈RnsD，不一定有-a∈RnsD.

定理6 设p,q∈R，且p2=p，q2=q，若p+q-1∈RsD，p+q∈RsD，则pq+qp∈RsD且

(pq+qp)nsD=(p+q-1)nsD(p+q)nsD=(p+q)nsD(p+q-1)nsD.

证明 假设p+q-1∈RnsD，p+q∈RnsD，因为，

(p+q-1)(p+q)=(p+q)(p+q-1)，

根据引理4，

pq+qp=(p+q)(p+q-1)∈RnsD，

(pq+qp)nsD=(p+q-1)nsD(p+q)nsD=(p+q)nsD(p+q-1)nsD.

引理9[9]设n∈，a,b∈RnsD使得a2b=aba，则ab∈RnsD.

定理7 设p，q∈R,且p2=p，q2=q使得pq=pqp，qp=qpq.若p-q∈RnsD，p+q-1∈RnsD，则pq-qp∈RnsD.

证明 假设p-q∈RnsD，p+q-1∈RnsD.令a=p-q，b=p+q-1，则有a,b∈RnsD，a2b=(p-q)2(p+q-1)=0，aba=(p-q)(p+q-1)(p-q)=0，即a2b=aba.根据引理9得，ab=(p-q)(p+q-1)=pq-qp∈RnsD.

注记3 定理7反过来不一定成立.

p2=p，q2=q，pq=pqp，qp=qpq.

显然pq-qp=0∈RsD，但是p-q=-1，根据引理1有，-1-(-1)2=1∉N(3)，从而有

p-q∉(3)sD.