幂级数和函数的求法

张海涛

（山西大同大学数学与统计学院，山西大同 037009）

幂函数的和函数的计算在高等数学中是教学重点,也是学习的难点，而且在考研中也是常见的考点。文献[1−3]总结了一些简单的方法，而课本上关于和函数的求法，例题和习题中的类型较少，因此，学习起来有一定的困难,把和函数的求法分三类进行讨论，给出了不同类型的级数计算的方法,希望对初学者在此部分的学习有引导作用。为了叙述简便，在解题过程中忽略收敛域的问题，总假设所有的计算都是在收敛域的范围内进行。

1 利用和函数的定义进行计算

和函数的定义是前n项和的极限,这种类型，就是最常见的级数和的公式，它的典型特点是n只出现在指数上。所谓越基础越重要,值得单独列出来熟练掌握，要熟练到看到就能写出，举几个例子：

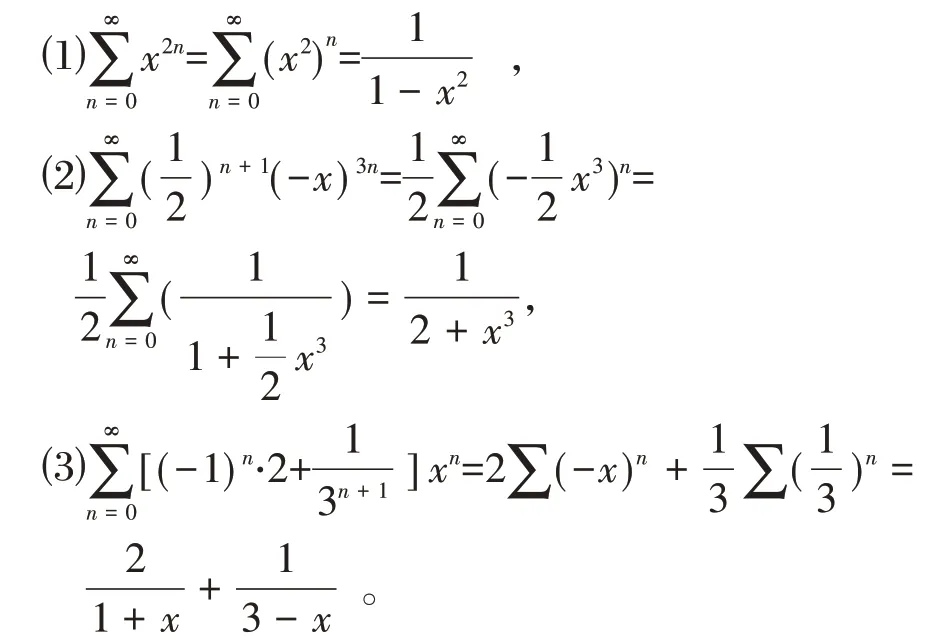
在实际解题过程中，要注意符号的下标，否则容易犯错误。比如:

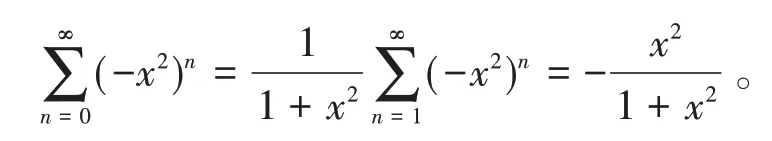
简单的方法就是看幂级数的第一项是什么，一般而言，基本型和式的分子就是第一项。

2 利用幂级数的逐项微分和逐项积分的性质

幂级数的和函数有如下性质

性质1幂级数的和函数在其收敛域上I可积,并有逐项积分公式

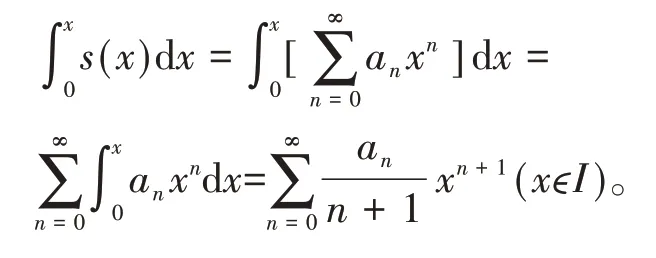
逐项积分后所得到的级数和原级数有相同的收敛半径[4]。

性质2幂级数的和函数在其收敛区间(−R，R)内可导，并有逐项求导公式

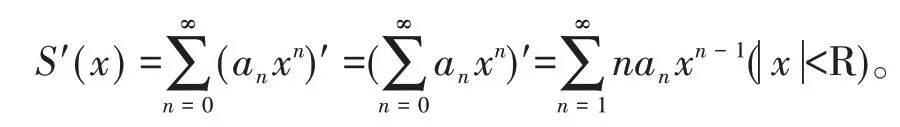
逐项求导后所得到的级数和原级数有相同的收敛半径[4]。

运用此类方法，或者先积分后求导，后者先求导后积分，或者求导求积分多次联合并用。这种类型最为常见，主要特征就是含的式子是有理式，若出现在分母中，考虑求导,若出现在分子中考虑积分。

3 利用幂级数展开式直接求和

常见的五大级数展开式

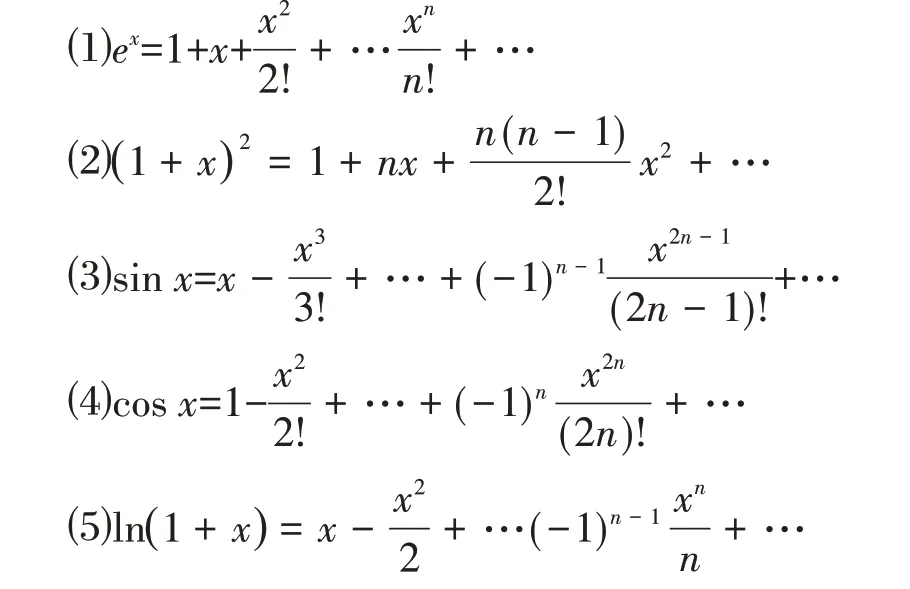
当幂级数的一般项系数的分母为n的阶乘时，常用此方法，一般是先找出与所给级数相近的某个初等基本函数的展开式，再进行尝试。这类型的题目常需要特别的技巧，计算量也较大，要掌握其方法，需要从易到难逐步熟悉。

令x=1，就得到所求结果为

幂级数的和函数的求法是级数这部分内容的重点和难点，在平时学习中要注重练好基本功，对于常见的方法要熟练掌握。除了文中的方法，还可以由已知幂级数建立关于和函数的微分方程求解，或者利用幂级数的下标变换求和函数。对于一些求数列前n项之和的，也可以转化为幂级数的求和问题。这类题目，难度较大，综合性较强。要通过勤加练习，加以巩固。