一种三对角矩阵的相似对角化及其应用
2021-11-19张兴刚
张兴刚,曹 磊
(1.贵州大学 物理学院,贵州 贵阳 550025;2.中国电建集团贵阳勘测设计研究院,贵州 贵阳 550081)
颗粒介质的静力学问题是颗粒物质研究中基础且重要的方面,它与实际应用密切相关(例如,工程中地基的承载能力、砂石骨料的受力结构,材料科学中颗粒材料的力学性能,等等),对于其它复杂体系(例如,悬浮液、泡沫、胶体等)的理解也有重要的意义[1-2]。人们在很早的时候就发现,筒仓中的粮食与水在静力学方面有很不相同的表现,粮仓底部所受压力会随粮食堆积高度的增加而趋于饱和,这就是颗粒物质静力学中一个著名的效应——粮仓效应[1,3]。早在1895年,德国工程师Janssen就提出了基于一定假设的连续介质模型,对粮仓效应进行解释。然而,颗粒物质是一种典型的复杂体系,目前还没有关于颗粒介质静力学的系统、成熟的理论,许多基本问题仍需深入探究。因此,自上世纪九十年代的颗粒物质研究热潮以来,仍有许多研究者对粮仓效应及相关的问题进行研究[4-13]。例如,最近有关反粮仓效应[11]和磁性颗粒体系粮仓效应[12]的工作。已有的研究工作以实验和计算机模拟为主,理论方面也主要是对Janssen模型、OSL模型等宏观唯象模型[4]的讨论,对于粮仓效应产生的微观机理以及唯象参数与微观结构的联系还不是很清楚。为了深入认识颗粒介质所服从的力学规律,很有必要加强颗粒体系的微观结构、力网、力传递等问题的研究,基于微观的几何和力学分析建立体系的微观特征与宏观性质之间的联系[13-15]。
对于圆盘的晶格堆积,文献[6]中通过结构和力学平衡的分析得到了相邻两层颗粒间力传递的规则,并且利用力传递规则得到了随着堆积层数增加容器底部总压力会趋向饱和的结果。对于非晶格的堆积结构,不借助计算机模拟很难从理论上直接进行结构和力学的分析。标量q模型是研究颗粒堆积中力的几率分布的一个著名的模型[15]。为了便于从理论上研究筒仓底部压力分布与顶部压力分布的关系,可以采用q模型的基本思想,将筒仓中随机堆积的颗粒体系抽象简化为格点系统。本文以二维筒仓中随机堆积的颗粒体系为物理背景,建立了一个由吸收系数p和侧向传递系数q决定的格点系统模型,该模型的解析求解涉及到三对角形式的传递系数矩阵A(p,q)的相似对角化。文中通过相似变换将A(p,q)对称化,并且提出基于二阶差分方程的方法对矩阵的特征值和特征向量进行分析和计算;最后,将相关的数学结果用于讨论粮仓效应的有关问题。
1 力传递的数学模型
为讨论问题方便,这里主要研究二维的情形,将粮仓效应中的物理体系抽象为图1所示的带有边界的格点系统。在格点系统中,一个格点等效于一小团颗粒,第m行n列的格点用符号P(m,n)表示,格点的总行数M≥2,总列数N≥5,并且每个格点都受到重力m0g的作用。类似于标量q模型,这里主要关注每个作用力在竖直方向上的分量,因此在下面的讨论中,所说的作用力一般是指力在竖直方向上分力的大小。顶部各个格点所受的压力可用行向量f0=(f01,f02,…,f0N)描述,底部各个格点对容器底的压力用fM=(fM1,fM2,…,fMN)描述。为了给出底部压力分布fM与顶部压力分布f0的关系,需要结合实际物理体系的特征定义恰当的相邻两层格点间力传递的规则。这里以随机堆积为物理背景,定义了图1所示的一种典型的力传递规则。规定同一行的格点间没有竖直方向的分力,不相邻的两行格点间也没有相互作用。对于任意格点P(m,n),称其所受的重力、顶部对其产生的压力、以及第m-1行格点对其产生的作用力为输入力;将P(m,n)对第m+1行格点、及其对容器的作用力称为输出力;对于每一个格点,只有上述五种竖直方向分力的存在,为了保证格点在竖直方向的力平衡,总输入力必须等于总输出力。图1中用实线箭头比较完整地画出了第一行格点的各个输入力及输出力的情况(重力没有画),图中的虚线箭头上也标出了每种输出力对应的系数。记P(m,n)所受的总输入力为wmn,总输入力向量wm=(wm1,wm2,…,wmn),重力向量b=(m0g,m0g,…,m0g),有,
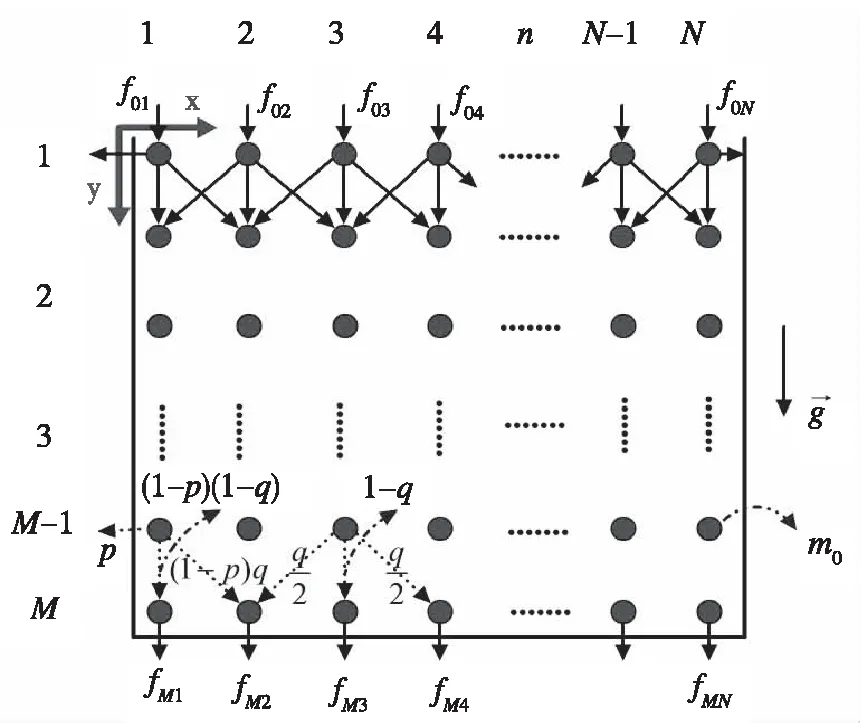
图1 格点系统模型中力的传递Fig.1 Rules of force propagation in the lattice system
w1=f0+b=(f01+m0g,f02+m0g,…,
f0N+m0g)
(1)
图1中定义的力传递规则,用数学语言表达就是当1≤m≤M-1时,有力传递方程
wm+1=wmA+b
(2)
其中,N阶矩阵
A(p,q)=

(3)
称其为传递系数矩阵,它是一个三对角矩阵[16]。传递系数矩阵只由p和q这两个参量确定,因此为了表述方便,称这个模型为pq模型。模型中的p称为吸收系数,反映了由于容器侧壁与颗粒的摩擦所导致的格点总输入力被器壁吸收的程度,它满足0≤p<1;若容器侧壁与颗粒无摩擦,则p=0,有摩擦时0 由图1中定义的力传递规则,有fM=wM;因此由(1)、(2)两式可以导出fM与f0的关系。假设存在可逆矩阵Q使A=QΛQ-1,并且假设A-E可逆(E是N阶单位矩阵),不难导出 fM=f0QΛM-1Q-1+bQ(Λ-E)-1(ΛM-E)Q-1 (4) 于是从理论上计算fM的关键在于考虑传递系数矩阵A的相似对角化以及矩阵A-E的可逆性。 D-1AD=B(p,q)= (5) (6) 为了给出矩阵P与Λ,需要求解B的特征值与特征向量。设xT=(x1,x2,…,xN)T是B的特征向量,λ是相应的特征值,那么应该有, (B-λE)xT=0 (7) 传统的方法是先由B的特征方程计算特征值,再将特征值代入方程组(7)求相应的特征值。与传统的计算方法不同,这里采用直接分析齐次线性方程组(7)的方法,通过同时进行特征值与特征向量的计算从而简化理论分析过程。将(5)代入(7)可得带有边值条件的差分方程, (8) 这个差分方程的边值条件比较复杂。引入新的变量yT=(y1,y2,…,yN)T,定义可逆变换yT=DxT;由(8)可得到关于yT的差分方程, (9) 由于B是对称矩阵,其特征值都是实数,因此只需在λ∈的范围内讨论方程(9)。可以根据二阶常系数差分方程的理论求(9)中差分方程的通解。该差分方程对应的特征方程为 (10) (1)第一种情况λ′2=1:方程(10)有二重解r1=r2=λ′,此时(9)中差分方程的通解为 yn=c1λ′n+c2nλ′n,1≤n≤N (11) 以y1和yN为边值,那么(11)中的待定系数c1与c2应该满足, (12) 这个方程组中系数矩阵行列式不为0,容易得到向量(c1,c2)T的唯一解,将其解代入(11)式有, (13) 利用(13)得到y2、yN-1关于y1、yN的表达式,考虑到λ′2=1并且将它们代入(9)中的边值条件有, (14) 记这个关于向量(y1,yN)T的方程组的系数矩阵行列式为det(p,q,N,λ′),显然λ′2=1所对应λ要成为特征值需要满足方程, det(p,q,N,λ′)=0 (15) 为方便起见,分两种情况进行讨论: ①当λ′=1时,方程(15)可写为 p(N-1)[2q(1-p)+p(N-1)]=0 (16) ②当λ′=-1时,方程(15)可写为 p(1-2q)(N-1)[p(N-1)-2q(1+p(N-2))]=0 (17) 利用λ=q(λ′-1)+1,(16)、(17)式,以及上述讨论过程不难得出下面的结论。 可将λ′=-1代入(14)式,给出(y1,yN)T的通解;然后利用(13)式得出向量yT,再利用xT=D-1yT并且单位化后就可得到结论2中相应于λ=1-2q的单位特征向量。 (2)第二种情况λ′2≠1:方程(10)有两个不同的根r1、r2,此时(9)中差分方程的通解为 可以用复函数简化问题的讨论,设自变量z定义在复平面上,复余弦与复正弦函数分别定义为 (19) 记集合S1={z|lmz=0},S2=Pz|Rez=kπ,k∈},S3=S1∩S2,显然S1就是复平面上的实轴,那么有, 定理1当且仅当z∈S1∪S2时,函数cosz取实数值;z∈S3时,cos2z=1;z∈S1-S3时,cos2z<1;z∈S2-S3时,cos2z>1。 定理2函数cosz与sinz的零点都在实轴上。 运用复数的知识不难证明这两个定理,这里不再赘述。利用根r1、r2的形式并且结合定理1,可以设λ′=cosz,不难得出r1=eiz、r2=e-iz;需要注意的是由于λ′∈、λ′2≠1,因此只需在z∈(S1∪S2)-S3的范围内讨论问题。于是(9)中差分方程的通解变为 yn=c1einz+c2e-inz,1≤n≤N (20) 以y1和y2为边值,那么(20)中的待定系数c1与c2应该满足, (21) 利用定理2易知该方程组中系数矩阵行列式在整个z∈(S1∪S2)-S3的范围内都不为零,容易得到向量(c1,c2)T的唯一解,将其解代入(20)式有, (22) 利用(22)得到yN-1、yN关于y1、y2的表达式,将它们代入(9)中的边值条件有, (23) 这个关于(y1,y2)T的方程组的系数矩阵行列式为 (24) 显然当λ′2≠1时矩阵B的特征值就由方程 det(z,p,q,N)=0 (25) 中z的解的情况决定。这是一个复杂的三角方程,可以通过令z′=ez从而将其转化为关于z′的高次代数方程;求出该高次代数方程的所有解便可得到B(p,q)的所有特征值,进一步可利用(22)式求出所有相应的特征向量,从而解决A(p,q)的相似对角化问题。但是,一般情况下只能求该方程的数值解,因此为了得出解析的结果只能对一些特殊的情况进行讨论。明显p=1/2、q=1是最简单、在物理上也属于比较典型的情形,因为它相当于筒仓系统中颗粒与器壁的摩擦不是很小也不是很大,并且颗粒团由于成拱效应明显而几乎不向其正下方传递力的情况。此时方程(25)为 sin(N+1)z=0 (26) (27) (28) 由结论1,当容器侧壁与颗粒有摩擦(即p≠0)时,1不是B(p,q)的特征值,易知这时矩阵A(p,q)-E是可逆的。因此p≠0时可以利用(4)式给出容器底部压力分布fM与顶部压力分布f0的关系。利用上面介绍的方法可以求出B(p,q)的所有特征值和特征向量,于是由(4)、(5)、(6)式可得, (29) 可以将这个公式用于讨论粮仓效应等力学问题。在粮仓效应的有关实验中,通常关注容器底部测得的有效质量Me(即底部的总压力与重力加速度g的比值)与容器中颗粒总质量Mt的关系。对于p=1/2、q=1这种典型的情况,如果容器顶部无压力,那么可由(27)、(28)、(29)式得到, (30) 其中,fMn是向量fM的第n个分量。在实际问题中更关心M和N远大于1时Me随Mt变化的大致情况。明显(30)式的求和部分只有当k取奇数时才有贡献,而且随着k的增大求和部分会迅速地减小并趋于0;于是对于近似地讨论问题可以取一级近似,得到, (31) 设M=h(N+1)2,其中h可间接地反映堆积的高度。当N>>1时(31)式简化为 (32) (33) 利用Janssen模型[1,4]可以得到Me=Ms(1-e-Mt/Ms),其中Ms叫作饱和质量;显然(33)式的结果与Janssen模型得到的结果很接近,这说明本文中的pq模型也可以解释粮仓效应,它在一定程度上正确反映了筒仓系统中力传递的特征。利用(29)式,还可以比较方便地讨论容器底部的应力分布、点载荷的响应等方面的力学问题。当然,如果要深入了解p和q对这些力学问题的影响,就需要求解方程(25);根据前面的数学讨论,在一般情况下应该结合数值计算才能解决这个问题。 为了从微观上理解粮仓效应,我们针对二维随机堆积建立了一个格点系统模型——pq模型。该模型的解析求解涉及到三对角形式的传递系数矩阵A(p,q)的相似对角化,这也是本文的重点。我们通过相似变换将A(p,q)对称化,并且提出基于二阶差分方程的方法比较有效地解决了该对称矩阵的特征值和特征向量的计算。对于p=1/2、q=1这种典型的情况,我们解析地导出了粮仓底部的有效质量随颗粒总质量的变化关系;其它p,q取值的情况也可转化为数值求解高次代数方程(25)的问题。本文讨论的pq模型只是格点系统模型中一种可能的力传递形式,对于不同的堆积结构和环境条件,可能具有不同的力传递规则,在数学上一般表现为不同的传递系数矩阵。本文提出的理论方法对于其它传递系数矩阵的情形有借鉴的价值,研究的结果也能加深对微观力传递规则与宏观压力分布之间关系的认识。2 矩阵A(p,q)的相似对角化
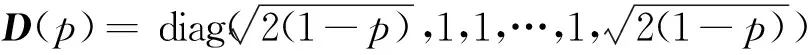
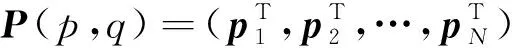
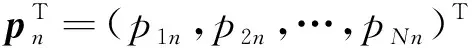
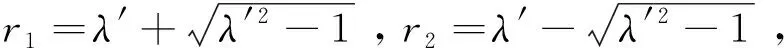
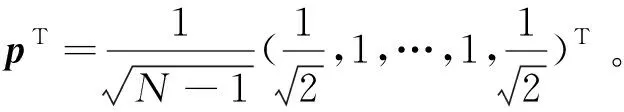
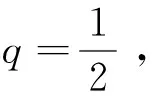
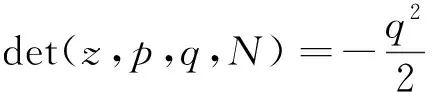
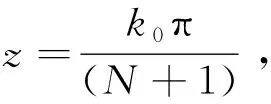
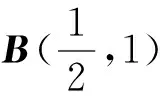
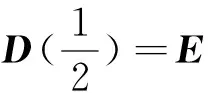
3 应用与讨论
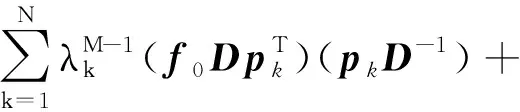
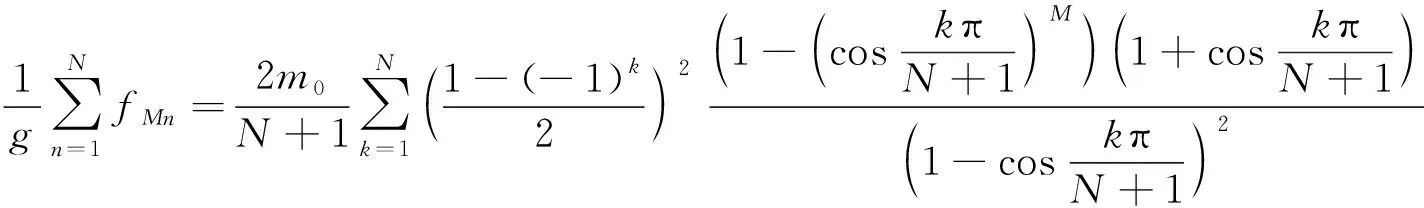
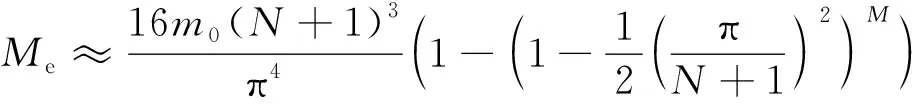
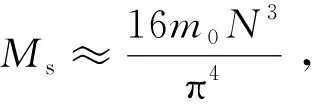
4 结论
