碰碰车低速正碰撞动力分析与比较

赵九峰

(河南省特种设备安全检测研究院，河南 郑州 450000)

随着社会的发展和大众生活水平的提高，休闲娱乐成为人们日常生活的一个重要组成部分，游乐设备也越来越受大众欢迎[1]，碰碰车作为一种传统的游乐设备，玩法多样，适合多人一起游戏，可以进行追逐、碰撞、围堵、反弹、抢位、对抗、配合打援等，每种游戏形式都可以获得不同的快乐。碰碰车是一种互动性和参与感比较强烈的游乐设施，是一款适合亲子、情侣、朋友之间一起参与的游乐形式[2]。

碰碰车在运行过程中，车体之间、车体与防撞梁不断发生碰撞，经常承受作用时间很短但幅度很大的碰撞冲击载荷。碰碰车周围都有一层缓冲胎，减小碰撞时的冲击力和对乘客人身安全的影响。传统的游乐设施结构计算中，采用一个放大的冲击系数考虑碰撞冲击载荷的影响[3]，设计时一般无法准确计算；同时游乐设备行业部分学者认为，碰碰车以额定速度对面正碰撞时效果要远大于碰碰车与静止的防撞梁碰撞效果。由于碰撞时间短、过程复杂，样机碰撞试验难以精确地测验碰撞过程中的受力变形[4]。为了解决当前碰碰车设计时碰撞冲击系数理论计算不精确，同时验算不同工况下碰撞效果的目的，以有限元仿真技术和结构动力学理论为基础，应用有限元工程分析软件[5]，对碰碰车的两种典型的正碰撞工况进行模拟分析和对比研究：

工况1：碰碰车和防撞梁正碰撞；

工况2：两辆碰碰车对面正碰撞。

1 运行原理

根据取电方式的不同，碰碰车分为天网碰碰车、地网碰碰车和电瓶碰碰车。其中的地网碰碰车由于故障率低，保养方便等优点，成为国内广泛流行的一种碰碰车。地网碰碰车通过地板提供电力，可以在整个地板上形成两个极性，车架下面的取电轮接触到地网取电。驱动系统采用直流电机驱动，前轮结构和驱动电机一体，可以360°旋转。碰碰车被一层橡胶缓冲胎包围，缓冲胎为橡胶材料，作为一种超弹性材料，具有回弹性强、变形量大、拉压性能好等特点，碰撞时具有缓冲吸能作用[3]。

碰碰车主要由车架、缓冲胎、操纵系统、驱动轮等组成，结构简图如图1所示。

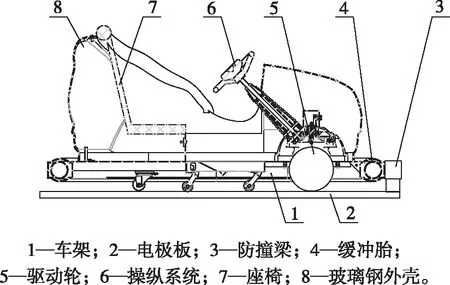
图1 碰碰车结构简图Fig.1 Bumper car structure diagram

2 理论分析

碰撞过程可分为两个阶段，以两辆碰碰车对面正碰撞为例，碰撞的第一阶段，缓冲胎在两车挤压下发生形变，两车的速度在形变产生的弹性恢复力作用下发生变化，形变达到最大时两车的速度相等，也称为压缩阶段；碰撞的第二阶段，缓冲胎由于形变开始反弹，在弹性恢复力作用下两车相互脱离接触，车速也随之变化，直到缓冲胎弹性势能完全释放，两车脱离，也称为恢复阶段[6]。

碰碰车碰撞的过程属于冲击载荷变形和非线性动态接触的过程[7]，在碰撞过程中将动能转化为其他形式的能，主要为缓冲胎的应变能，由于橡胶为回弹性强的材料，最后缓冲胎的应变能再次转化为碰碰车的动能，因此碰碰车的碰撞可以视为物理学中的完全弹性碰撞。碰碰车的相互作用阶段可以简化为近似的质量-弹簧系统模型描述。碰碰车两种工况碰撞力学模型如图2所示。

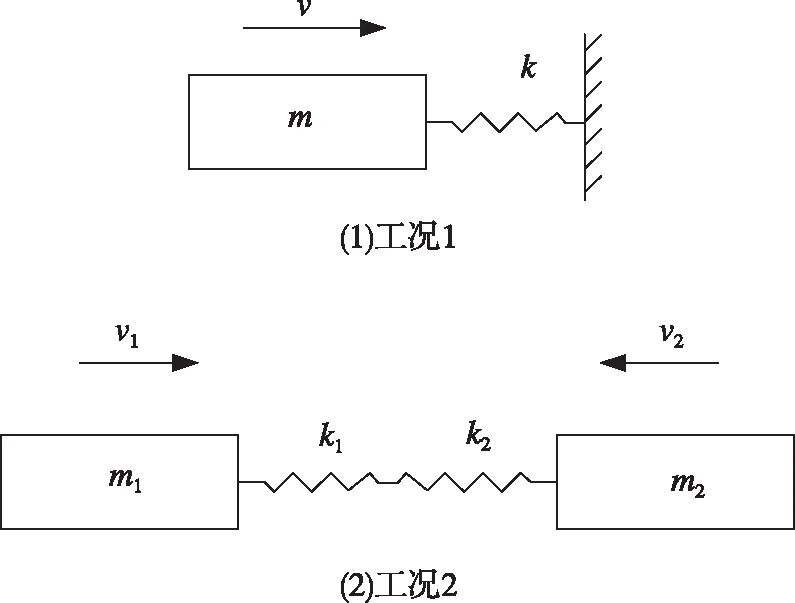
图2 两种碰撞工况的力学模型Fig.2 Mechanical models of two collision conditions

理想状态下完全弹性碰撞没有机械能损失，即同时满足动量守恒定理和机械能守恒定律[8]：

动量守恒方程：

(1)

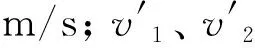
机械能守恒方程：

(2)

由公式(1)可知，两物体相同质量和相同速度相对正碰撞(m1=m2=m，v1=v2=v)，最终两物体以相同的速度弹开，速度大小不变，速度方向相反。同时碰撞的压缩阶段结束瞬间，两车的速度为0，此时对单个物体，动能完全转化为弹簧的应变能Ek，J，由胡克定律可得

(3)

式中：k为弹簧的劲度系数，对两个相同物体相碰，k1=k2=k，N/m；Δx为单根弹簧的最大压缩量，m。

3 有限元模型

瞬态动力学分析可以用来对承受碰撞冲击的结构的动力响应过程中的能量、速度和应力强度进行模拟计算[9]。利用ANSYS Workbench软件的瞬态动力学分析模块Transient Structure对碰碰车两种碰撞工况进行仿真模拟，求解碰撞过程中的能量、速度和应力随时间的变化。

依据本次碰撞仿真的试验目的以及碰撞过程中的变形特点，为保证计算准确、减小计算规模并使模型能够反映碰碰车真实的力学特性，对碰碰车结构进行适当简化[10]，忽略碰碰车玻璃钢外壳、操纵系统、驱动轮等，在车架结构上附加质量单元(point mass)，用来模拟乘客和座舱等质量。

碰碰车满载时的总质量m=420 kg(含2名乘客)，碰碰车架和防撞梁材料为Q235B，缓冲胎的材料为橡胶，碰撞前碰碰车的最大水平速度v=1.5 m/s。在建模、加载及求解过程中不考虑材料塑性影响[10]，定义各部分的材料属性，材料属性如表1所示：

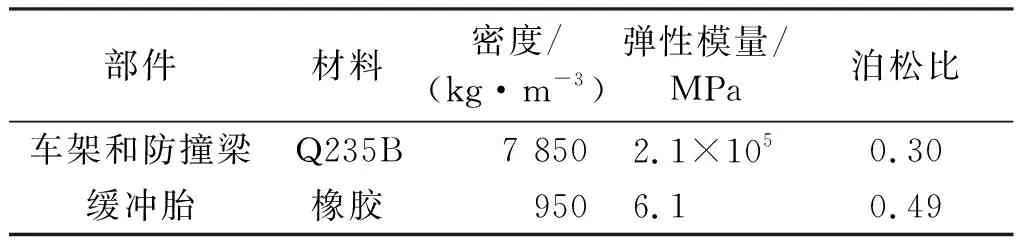
表1 材料的力学性能[11]Tab.1 Mechanical property of main materials[11]

缓冲胎为赋予橡胶材料，碰碰车和防撞梁由型钢和钢板焊接而成，赋予Q235B材料，以板壳为主建立有限元模型，即采用4节点的壳单元SHELLl81，使用四边形和三角形混合单元，在缓冲胎与防撞梁的可能接触部位，因碰撞接触产生应力，对网格进行细化。防撞梁设为刚性体，其它部件为柔性体，两种碰撞工况下的有限元模型如图3所示。

图3 有限元模型Fig.3 Finite element models

对可能发生碰撞的部位施加面-面无摩擦接触(frictionless),为了避免单元节点相互穿透，接触算法选择法向拉格朗日(normal Lagrange),对于碰撞冲击类型，时间步控制选择预测碰撞(predict for impact)[12]。车架底部施加竖直方向平动位移约束(displacement)，定义初始速度，在初始条件下定义车速为1.5 m/s，在整个分析过程中，初始速度仅仅是碰撞前的初始值。

4 碰撞分析

4.1 分析设置与结果提取

对碰碰车的两种碰撞工况进行碰撞仿真分析，使用Newmark时间积分的方法在离散的时间点上求解，两个连续时间点之间的时间增量称为积分时间步长(integration time step)，算法可以自动调节至适合的步长，使误差的估计逐渐趋于零，从而得到这种有效方法可靠的数值解[13]。初始时间步为0.005 s，最小时间步为0.001 s，最大时间步为0.01 s。考虑缓冲胎在碰撞过程中的大应变，打开大变形设置(large deflection)；考虑碰撞体之间动量交换和惯性效应，打开时间积分设置(time integration)，用于计算结构冲击或快速的时变载荷下的结构动态响应[14]。总分析时间设为0.1 s，求解完毕通过后处理查看两种工况下的分析结果，提取两种工况下数据曲线进行对比分析。分析结果如图4所示。

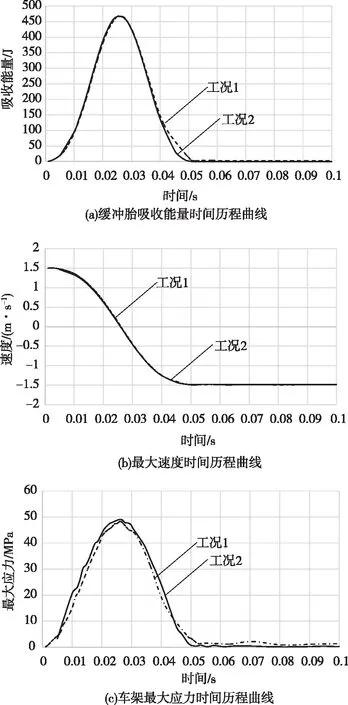
图4 两种碰撞工况的分析结果对比Fig.4 Comparison of analysis results of two collision conditions

4.2 仿真结果分析

两种工况下单个缓冲胎的低速吸能时间历程曲线如图4(a)所示，两种碰撞工况下的缓冲胎总吸收能量曲线基本一致。在压缩阶段，碰撞时能量吸收不断增加，直至0.025 s左右吸能曲线达到峰值[15]，而后进入恢复阶段，能量开始释放，0.05 s后能量释放完毕，碰撞结束。碰撞过程中最大吸收能量为468 J。碰撞过程中最大吸收能量的理论值由公式(3)可得

两种工况碰撞过程中缓冲胎吸收能量的仿真值与理论值的误差小于1%，仿真结果略小于理论计算值，说明还有不到1%的动能转化为车架的应变能，表明缓冲胎起到很好的缓冲吸能作用。

两种工况下单个车辆的最大速度时间历程曲线如图4(b)所示，两种碰撞工况下的速度曲线基本重合。碰撞前的速度为1.5 m/s，在0.025 s时瞬时碰撞速度为0，碰撞结束后，即在0.05 s时，速度为-1.5 m/s(负号表示反向)。碰撞前后速度大小没有变，速度的方向相反，与理论分析吻合。

两种工况下车架的最大应力时间历程曲线如图4(c)所示，两种碰撞工况下车架的最大应力曲线基本吻合。图中可以看出，在0.025 s时，车架应力达到最大峰值，车架的最大应力为49.5 MPa，0.05 s碰撞结束后，车架的应力趋于0。

5 结语

利用有限元软件ANSYS Workbench的瞬态动力学分析模块，对两种碰撞工况下的碰碰车建模和分析，进行碰撞冲击模拟计算，提取两种工况下的吸收能量、最大速度和最大应力的时间历程曲线，并进行对比分析和研究，分析结果表明：

1)两种工况下的瞬态动力学分析，吸收能量和速度的仿真结果与理论分析一致，表明仿真分析的过程可靠性与结果合理性。

2)碰碰车的吸收能量曲线、最大速度曲线和最大应力曲线在两种碰撞工况下几乎重合，表明在质量和速度相同的条件下，碰碰车与静止的防撞梁正碰撞与两辆碰碰车对面正碰撞时效果相同，可以用碰碰车与防撞梁的正碰撞代替两辆车对面正碰撞去验算校核碰碰车的结构强度。

3)碰碰车的缓冲胎在碰撞过程中吸收总动能的99%，起到很好的缓冲吸能作用。