新冠疫情对高速公路交通量的影响评价
2021-11-18武亚鹏李慧颖卢冬生许熳灵
武亚鹏,李慧颖,卢冬生,许熳灵
(中南勘察设计院集团有限公司,湖北 武汉 430073)
受2020年新冠疫情影响,我国经济受到了冲击,其中交通运输、旅游等服务行业受到的影响最大[1],第一季度同比下降5%以上。根据疫情防控需要,2020年1月23日至4月8日,武汉市及湖北省内其他城市陆续采取封城、交通管制等隔离措施,湖北省高速公路交通量急剧下降。同时,2020年2月17日至5月6日国务院对全国高速公路采取免费政策,高速公路运营企业通行费收入受到严重影响[2]。因此,有必要对高速公路交通量受此次疫情的影响程度进行研究分析,揭示相关机理,寻找相应对策。
疫情对交通运输业、旅游业造成影响的相关研究可分为两类,下面分别进行介绍。第一类是通过建立预测模型对入境旅游人数、客运量、经济等研究对象进行分析:孙根年等[3]利用本底趋势值方法,建立SARS确诊人数与客运量之间的空间统计模型,分析二者之间的相关性;朱迎波等[4]以疫情危机过程中人们的心里变化趋势为轴线,采用ARIMA模型对SARS影响初期、恢复期等阶段中国入境旅游人数进行了分析;肖海军等[5]采用多阶方程拟合,利用干扰函数改进的方式,建立了SARS危机后期旅游人数预测模型;桂文林等[6]采用ARIMA模型,建立了铁路客运量本底趋势值计算模型,并评估了SARS事件对铁路客运造成的影响;Fathima T K等[7]、Kuo H I等[8]均采用ARIMA模型研究禽流感、H1N1流感等传染疾病对旅游业造成的影响;闫明月等[9]依据百度指数与2019年全国高速流量数据,采用神经网络方法建立了疫情对全国高速流量影响分析模型。第二类是通过一些相关数据统计,定性地分析疫情危机对旅游业、铁路客运量等方面的影响:Khan H等[10]对传染病、森林火灾等危机影响下新加坡旅游业变化趋势进行阐述;曾本祥等[11]对SARS疫情期间中国旅游业相关数据进行统计分析,定性地阐述短期危机对旅游业的影响;吕宛青等[12]则详细梳理了2020年云南省接待游客数量,分析新冠疫情对旅游业的影响。
综上所述,国内外专家学者更趋向于采用损失率等指标来定量评价疫情危机对交通运输业、旅游业造成的影响,是由于此类方法具有直观性、准确性等突出特点,能够揭示相关影响机理。其中的ARIMA模型和回归模型在分析过程中应用较为广泛,属于成熟模型,而且ARIMA模型具有无需依靠外生变量、操作简单、响应迅速的优点。因此,文中以高速公路交通量作为直接研究对象,以经济恢复程度及疫情发展趋势为依据,采用时间序列分析、回归分析等多种方法,建立疫情对高速公路交通量影响的定量分析模型。
1 高速公路交通量本底趋势值预测
依据本底趋势值理论,高速公路交通量本底趋势值是指在不受新冠疫情影响下,高速公路交通量(收费流量,下同)按照正常环境所应有的发展趋势和时间规律。
文中选取湖北省某高速公路(以下简称:A高速公路)为研究对象,采用时间序列法[13]对其2020年交通量本底趋势值进行研究。时间序列法在交通量预测中应用较为广泛[14],主要是利用历史交通量数据,分析交通量一般变化趋势,并将此趋势向后推延,从而推算出未来交通量。按时间序列法的基本分析思路可将模型分为指数平滑、季节分解、回归模型及ARIMA模型4类,其中的ARIMA模型是国内外应用较为广泛的一种方法,其能够综合考虑各种变动因素,具有良好的精度,因此,文中采用ARIMA模型对A高速公路交通量本底趋势值进行预测。
ARIMA模型简记为ARIMA(p,d,q),共包含3个部分:自回归模型AR(p),移动平均模型MA(q)以及差分次数d(一般情况下d<2)。ARIMA(p,d,q)模型结构为
r(B)▽dyt=θ(B)εt
(1)
式中:yt为t时间节点高速公路交通量数值;▽d=(1-B)d,d为差分次数,B为延迟算子,且Bnyt=yt-n;r(B)=1-r1B-r2B2-,…,rpBp为自回归系数多项式,p为自回归阶数,r1,r2,…,rp为自回归参数;θ(B)=1-θ1B-θ2B2-,…,θqBq为移动平滑系数多项式,q为移动平均阶数,θ1,θ2,…,θq为移动平滑系数;εt为残差或白噪声序列。
文中以A高速公路2018—2019年共24个月的路段平均交通量作为基础数据,通过SPSS采用“专家建模”的方法进行ARIMA(p,d,q)模型计算。计算结果显示:ARIMA(0,2,6)模型的平稳R2为0.682,显著性为0.038(ρ<0.05),因此,模型拟合度良好,并向后预测12期的A高速公路路段平均交通量,将其作为2020年月平均日交通量的本底趋势值。
2 新冠疫情期间交通量统计分析
2.1 新冠疫情危机生命周期分析
胡鞍钢[15]、郭捷等[16]、郑拓[17]、陈恩等[18]均认为疫情突发事件具有生命周期性,因此,依据斯蒂文·芬克的危机4阶段生命周期模型,将此次新冠疫情危机分为征兆期、爆发期、高峰期、后疫情期4个阶段,具体时间节点及各阶段与高速公路相关政策梳理如表1所示。

表1 新冠疫情发展各阶段对高速公路交通量影响
2.2 新冠疫情各阶段交通量变化情况统计
统计了A高速公路收费站2019年12月1日至2020年2月29日的日交通量(见图1)。统计显示:2019年12月28日受元旦假期影响,收费站日交通量出现激增;2020年1月1日起收费站日交通量开始明显下降,至1月7日逐步又恢复至前一个月的平均水平。由此可见,疫情征兆期对高速公路交通量影响较小。

图1 A高速公路收费站2019年12月1日至2020年2月29日的日交通量
2020年1月23日武汉市发布封城通告,至26日A高速公路收费站日交通量急剧下降至400 veh·d-1左右。由此可见,疫情爆发期及高峰期由于各项疫情防控政策以及出行意愿的下降,高速公路交通量出现断崖式回落。
同时,文中统计了2018年1月至2020年12月A高速公路路段月平均日交通量的本底趋势值与实际值(见图2)。统计显示:随着抗疫工作获得阶段性胜利,国内经济逐步恢复,至2020年9月,高速公路交通量基本恢复正常水平。由此可见,后疫情期高速公路交通量开始逐步恢复,至9月份达到正常水平。

图2 A高速公路2018年1月至2020年12月路段月平均日交通量实际值与本地趋势值
2.3 高速公路交通量损失率计算
依据A高速公路2020年交通量本底趋势值以及实际值计算其损失率,具体算式为
βl=(yb-yr)/yb
(2)
式中:βl为A高速公路交通量损失率,yb为交通量本底趋势值,yr为交通量实际值。
计算结果显示:A高速公路交通量损失主要发生在2020年1月至8月之间,其中第一季度损失率达到86.38%,第二季度损失率达到41.47%,7月和8月约为10.69%,全年损失率约为24.04%。1月 末至4月末受疫情防控政策影响,其交通量损失可直接预见,而5月至9月(后疫情时期)处于交通量恢复阶段,且存在小范围的疫情反复,其交通量变化机理具有较高的研究价值,因此,文中重点研究后疫情时期高速公路交通量预测模型的建立。
3 后疫情时期高速公路交通量预测
文中采用回归的方法,重点分析后疫情时期高速公路交通量变化趋势,研究疫情与交通量之间的相关机理。
3.1 自变量和因变量选择
选取新增感染人数、境外输入人数、百度指数(新冠肺炎,武汉)、当月地区生产总值、当月高速公路收费天数等影响因素作为模型自变量,因变量则选择A高速公路的月平均日交通量(收费流量,下同)。
3.2 自变量标准化处理及筛选
为消除自变量之间量纲和数量级差异带来的影响,确保结果的可靠性,需要对原始数据进行标准化处理[23]。由于选取的自变量中存在为0的情况,因此,选用z-score法(正规化方法)对自变量进行标准化处理,算式为
(3)
式中:yi为第i个自变量标准化后的数据,xi为第i个自变量原始数据。
针对初选自变量与因变量进行相关性分析(见表2),结果显示:新增感染人数、当月地区生产总值、当月高速收费天数与因变量呈显著相关(ρ<0.05)。因此,在自变量中将百度指数(新冠肺炎,武汉)和境外输入人数去掉。

表2 自变量与因变量显著性相关分析结果
3.3 预测模型的建立
1)首先,采用主成分分析法对自变量进行降维处理,使用SPSS软件计算主成分荷载向量为
(-0.833,0.945,0.836),特征值分别为2.286、0.576、0.170,选取特征值大于1的为主成分,即提取到1个主成分,记为第1主成分,特征值为2.286,占总方差的76.2%。第1主成分系数是由主成分荷载向量除以其特征值算数平方根得到,经过计算可得新增感染人数、当月地区生产总值、当月高速收费天数3种自变量的主成分系数,值分别为(-0.550,0.625,0.553),即第1主成分表达式为
x′=-0.550x1+0.625x2+0.553x3
(4)
式中:x′为第1主成分;x1,x2,x3分别为新增感染人数、当月地区生产总值及当月高速收费天数。
2)其次,针对第1主成分,采用一次线性、二次曲线、三次曲线、复合曲线、对数、幂、指数、Logistic等多种方程形式与因变量进行拟合分析,得到三次曲线拟合度为最好结果,具体如表3、图3、图4所示。在图3中,复合、指数及Logistic三者的回归方程一致,故线条重合。

图3 主成分与因变量拟合曲线

图4 2020年模型预测结果与实际值对比
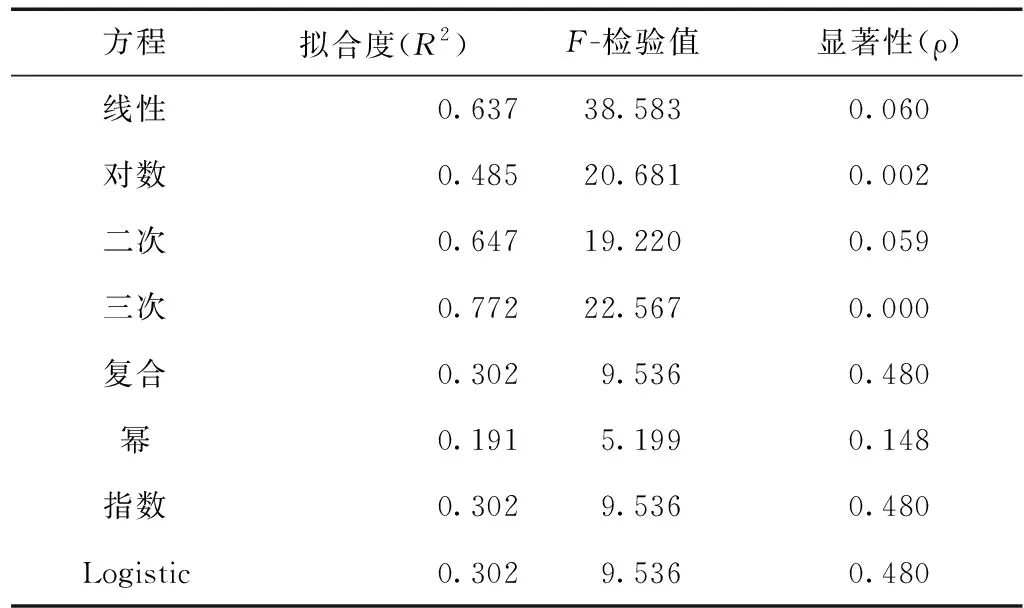
表3 主成分与因变量各拟合方程拟合度
因此,文中选择三次曲线方程将第1主成分与因变量进行拟合,从而得到A高速公路月平均日交通量的预测式为
6.88x1x2+6.91x2x3-6.08x1x3)-1.90x1+
2.61x2+1.91x3+2 508.90
(5)
式中:yk为A高速公路月平均日交通量预测值;x1,x2,x3分别为新增感染人数、当月地区生产总值及当月高速收费天数。
总体看,疫情影响下预测值与实际值误差应控制在±5%以内,处于可接受范围,表示该模型能够在封城措施解除后,根据疫情发展趋势、经济恢复程度及收费天数等因素有效判断高速公路交通量(收费流量)的变化情况。
4 结 语
1)受新冠疫情影响,湖北省A高速公路收费的车流量2020年全年损失率在24%以上,疫情爆发期及高峰期受管控措施及免费政策影响,收费车流量损失率接近90%,后疫情时期随着经济复苏逐步恢复至正常水平,损失率约为10%。
2)后疫情时期并未出现明显的报复性出行数据(由于节假日7座及以下客车免收通行费),上半年损失未得到充分补偿。对于高速公路运营企业来说,面临着债务违约、信用等级下降等诸多风险,应充分利用现有政策,积极争取延长经营期限、财政补贴以及税收优惠等补偿。
3)此模型未充分考虑收费标准调整、收费减免等国家政策以及局部疫情防控措施对高速公路交通量带来的影响,只是单纯依靠数据解释交通量波动,存在一定局限性,在后续研究中将考虑引入解释变量,丰富自变量类型,改进预测模型。
