轨道不平顺的评价检测及噪声处理方法

胡哨刚，孔祥芳,叶海波，肖志锋，冯 博，旷利平

(1.湖南高速铁路职业技术学院, 湖南 衡阳 421000；2.中国铁路广州局集团有限公司,广东 广州 510000)

轨道的平顺性不仅与铁路行车安全密切相关，同时也影响旅客乘车的舒适度，轨道的平顺性已成为当前衡量线路质量的关键指标[1-3]。国内外学者在轨道不平顺研究方面开展了大量工作，尤其在轮轨激励影响方面的研究成果颇丰。Dumitriu等[4]通过数值模拟来计算评估转向架的振动行为；Kedia等[5]利用列车与轨道的相互作用模型研究对列车诱导振动和噪声的影响；Wang等[6]建立轴承热分析模型分析高速铁路轨道不平顺对牵引电机轴承热特性的影响；李再帏等[7]从轮轨动力学角度建立行车安全性的极限状态方程；王平等[8]建立一种车轮不圆顺幅值快速测量模型进一步研究轨道谱；林玉森等[9]、陈杨等[10]分别探讨桥上列车走行性及高速列车小幅蛇行运动与轨道不平顺之间的关系。

在轨道不平顺评价研究方面，选用的研究对象为轨道谱和轨道质量指数(TQI:Track Quality Index)。陈果等[11]分析了目前广泛应用的几种轨道不平顺模拟方法，构造了基于频域功率谱等效的新算法；陈宪麦等[12]利用Welch改进周期图算法获得秦沈客运专线功率谱密度( Power Spectrum Density)；练松良等[13]利用计算机动力模拟仿真计算轨道不平顺激扰下客车和货车的动力响应；杜振军等[14]通过HHT边际谱提取铁路轨道不平顺频率结构信息；高望翰等[15]、余翠英等[16]和高建敏[17]利用改进的Welch周期图法，验证中国高速无砟轨道原始谱优于德国和美国；张煜等[18]、杨雅琴等[19]分别尝试建立轨道不平顺状态评价模型和劣化自适应分段模型；钱雪军[20]提出采用遗传算法进行最佳滤波器的设计；Li等[21]设计轨道不平顺性指标的相关分析方法。

在预测研究方面，James[22]根据分形理论对轨道平顺性进行评价，并利用双分析的方法实现对高低不平顺的预测;朱洪涛等[23]、赵隽等[24]建立自回归积分滑动平均模型(简称ARIMA)，分别对杭深线潮汕站4条到发线和盘营高铁下行区段进行轨道不平顺预测。回归分析建立的预测方程是基于自变量的变化来探索TQI的变化，当前影响TQI的因素比较繁杂，因此，无法据此建立准确的回归方程；李仕毅等[25]提出一种基于灰色成分数据模型的轨道不平顺指标结构预测模型，灰色预测对于波动性较大的数据拟合较差;针对轨道不平顺具有较强非线性的特点，彭丽宇等[26]用BP神经网络方法对重载铁路轨道不平顺的7项参数进行预测，但BP神经网络在推理过程中采用的线路有时不太灵活，这也影响最终的推理结果；卡尔曼(Kalman)滤波是以估计预测状况与真实状况之间均方误差最小为目标的一种滤波方法，可以预估信号过去和现在的状况，甚至预估将来状态，计算量相对较小，因此，被广泛应用于铁路、通信、导航、制导及控制等多个领域[27]。

当前关于轮轨激励影响及轨道谱方面的研究较多，而对轨道检测数据的修正和去噪研究较少，且采用的方法缺乏对噪声的分类处理。TQI数据通常为非等时距，不进行分类去噪处理，不仅采集的检测数据误差较大，也影响最终的预测精度。基于此，文中结合TQI轨道质量指标，在对动静态检测方法进行比较的基础上，通过对京广下行线开行轨检列车进行轨道动态检测，针对收集到的轨道病害检测数据，提出不良数据筛选原则及修正方法，引入卡尔曼滤波方法对数据进行去噪，并在京广下行线验证去噪处理效果。

1 轨道不平顺性评价方法

目前，工务部门进行轨道不平顺评价时主要采用TQI、峰值扣分法及轨道谱方法。峰值扣分法局限于仅反映轨道局部病害的类型及位置，缺乏对线路完整区段病害和状态的全面评价。轨道谱全称为轨道不平顺单边功率谱密度，能够清晰地刻画某一段随机轨道不平顺中包含的波长信息及波长对应的谱密度值，TQI为在200 m范围内综合评价轨道整体质量的一种评价指标。TQI及轨道谱可以对轨道整体的平顺性水平进行有效反映，能够为后续轨道不平顺性的发展趋势提供准确数据。TQI的算式为

(1)

我国200 m区段具体速度等级对应的TQI标准值如表1所示。

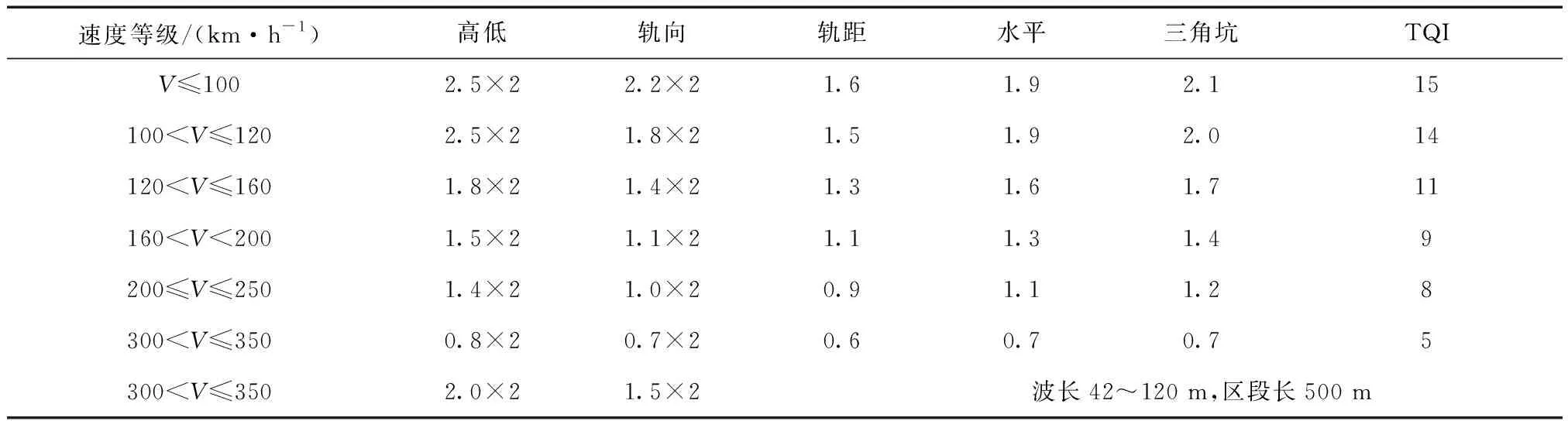
表1 我国200 m区段具体速度等级对应的TQI管理标准 mm

2 轨道病害检测数据采集及分析

2.1 轨道不平顺性检测方法比较

静态检测是指轨道在不受轮轨作用力时的几何尺寸状态，通常采用人工或轨检仪对线路轨道进行测量。轨检仪是一种利用电子传感技术对线路内部几何尺寸进行测量并保存的仪器。轨检仪相对于手工检测来说，检测水平及效率有了较大提高。动态检测是指开行轨检列车通过某轨道线路区段时，对列车横向、垂向加速度及乘车安全性和舒适性等的评价，并由轨道检测列车按照惯性基准法，将检测到的TQI各项指标数据实时显示为波形记录图，存储于计算机磁盘。

相对于轨道的静态检测，动态检测指标更能体现车辆在轨道上的真实运行效果。其原因在于轨道的动态检测不仅能体现轨道的静态几何状态对车辆运行的影响，还可反映出动力车辆、轨道、路基等对行车安全与舒适度的影响。动态检测的优势在于检查项目更完全、精准度更高、可靠性更强、技术上更先进，数据处理能力也更强大。

2.2 轨道病害动态检测数据采集

在京广下行线开行轨检列车采集多段轨道不平顺数据，轨道波形如图1所示。

图1 轨道病害波形

由波形图可以看出，京广线普遍存在的病害为高低、三角坑不良、轨距变化不良、曲率与超高逆向不平顺、轨向与超高逆向不平顺、整公里横加和垂加峰值偏大，变化较急促，线形不柔和。

3 轨道不平顺的检测数据去噪

在获取轨道不平顺数据的过程中，由于检测环境及设备影响，通常检测数据中包含有噪声成分。为了能够后续准确地对轨道不平顺状态进行评价，需要对检测原始数据中的噪声进行处理。在实际检测数据中，主要包括局部粗大异常值及噪声两种误差。

3.1 不良数据的筛选原则及修正方法

由于检测系统涉及的传感器较多，其检测环境相对较为恶劣，检测过程也是动态的，因此,在TQI指标检测过程中会有振动等多个因素影响检测数据的准确性，特别是会出现数据丢失、异常增大的突变值等情况。在计算轨道质量参数时，需要对这些异常数值进行处理。

由于轨道是连续的，且钢轨具有一定刚度，相邻检测点之间的距离间隔较小，变化过渡相对较为平滑，因此，相应的轨道参数不会发生突变。基于此，对于丢失的数据可考虑通过前后相邻点参数均值来代替，得到的估计值为

(2)

当选用参数个数n较小时，得到估计值可能受局部检测点的噪声影响较大；当选用参数个数n较大时，得到估计值受噪声影响较小，但会受到距离点较远轨道参数值的影响。因此，参数个数n的选择不宜过大或过小，通常为4～6个比较合适。

对于局部的异常突变值，可通过拉依达准则进行剔除，即3σ原则。假设轨道质量中各参数的检查数据仅含随机误差，对一定检测区间内的数据进行计算可得到均值和标准偏差，根据3σ原则，实际偏差在[μ-3σ,μ+3σ]上的概率为0.997 4，对于超过[μ-3σ,μ+3σ]的误差，定义为粗大误差，对异常粗大数据进行删除，对删除掉的异常突变值，同样可考虑使用相邻检测均值进行估计。

3.2 基于Kalman滤波的数据去噪

解决随机线性离散系统的状态或参数估计问题可选用卡尔曼(Kalman)滤波方法，建立离散随机差分方程预估离散时间的过程变量，相关参数如表2所示，算式为

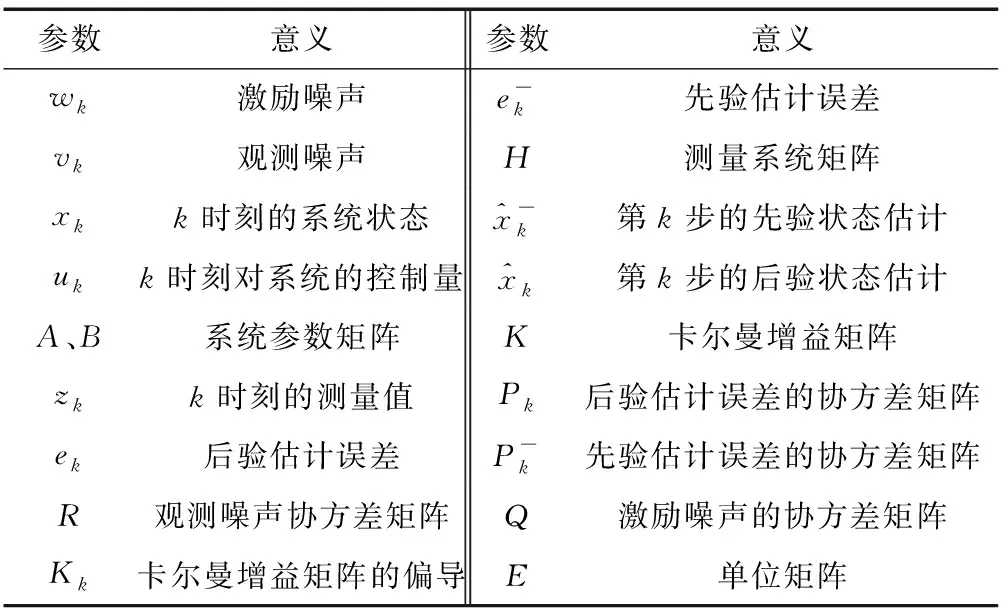
表2 相关参数说明

xk=Axk-1+Buk-1+wk

(3)

根据观测方程，可得到对应的观测变量为

zk=Hxk+vk

(4)

定义系统状态的先验估计误差和后验估计误差分别为

(5)

则协方差矩阵为

(6)

(7)

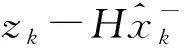
(8)

令一阶导数为0，对K求偏导可得

(9)

(10)

(11)

同理，得离散Kalman滤波状态更新方程为

(12)

(13)

(14)

3.3 实证分析

1) 2月25日在京广下行(1 337.600～1 567 km)0.2 m处采集数据进行经典Kalman滤波去噪处理，以左右轨向为例(见图2)。由图2左右实测轨向数据滤波对比看，Kalman滤波效果较好，实时性强，能够有效去除高斯噪声及非高斯噪声。

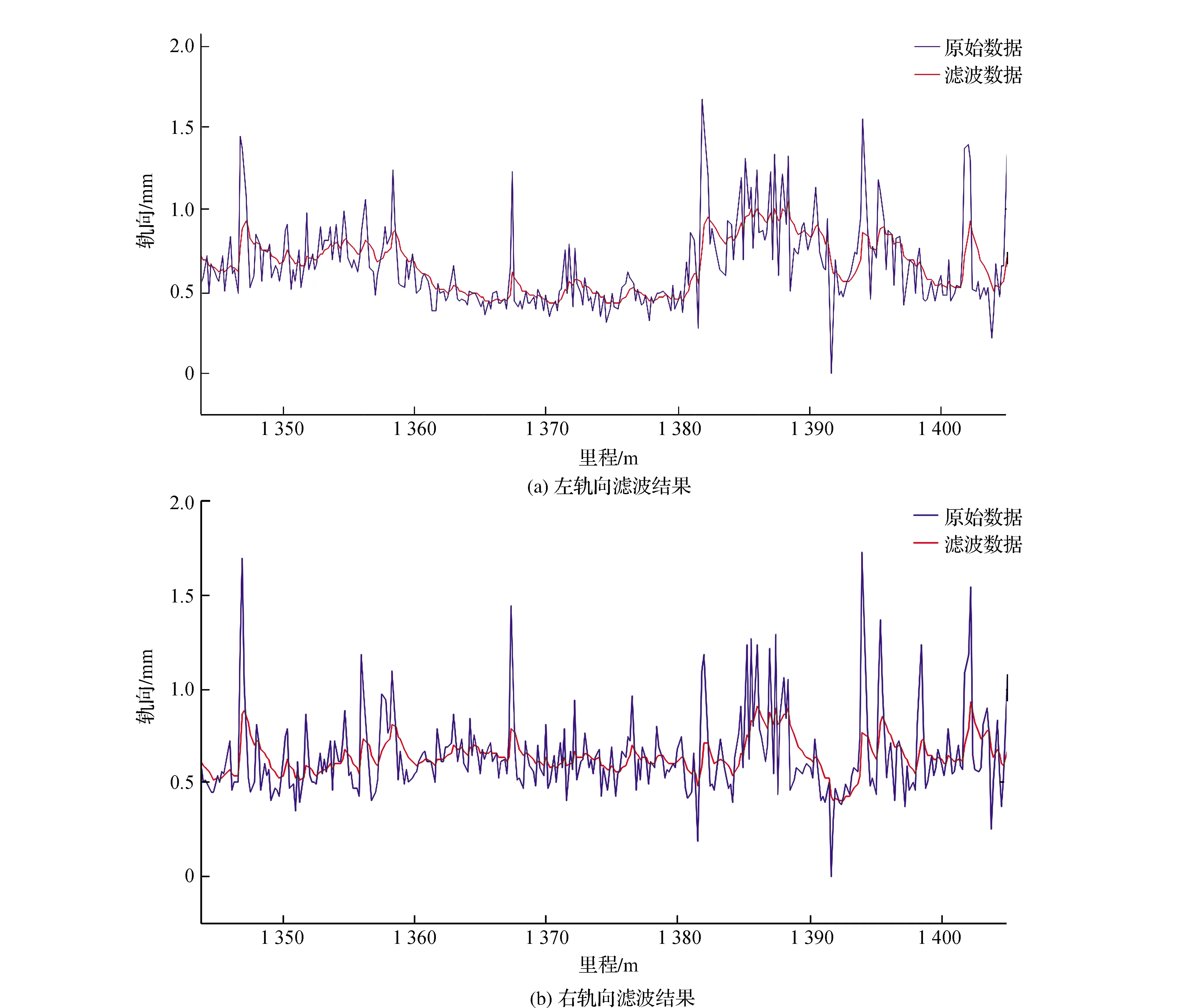
图2 实测轨向数据Kalman滤波结果对比

2) 选取未进行Kalman滤波去噪的线路与经过滤波去噪后的线路做精调后的实证比对，如图3所示。从图3检测数据波形比对看，未采用Kalman滤波去噪为导向线路的左高低问题消灭不彻底，线路平顺质量仍较差。

图3 检测数据波形比对

4 结 论

1) 相对于峰值扣分法只能对轨道进行局部不平顺评价，TQI及轨道谱方法不仅能反映出轨道整体的平顺性水平，而且可为轨道发展预测趋势提供准确数据；相对于静态检测，轨道动态检测指标更能体现车辆、路基、道床及轨道等对铁路行车安全带来的作用与影响。

2) 将经典卡尔曼滤波方法应用于京广线实例中，在对不良数据筛选及修正后，进行去噪处理，结果显示滤波效果相对较好。与未采用Kalman滤波去噪为导向的线路作精调后的TQI指标对比，采用Kalman滤波去噪的线路明显轨道平顺质量更高。

3) 对于京广线轨道病害可采取以下整修措施：一是提高作业标准，精简细修，重点解决短波病害，尽量消除4mm左右的水平短波变化，整修峰值超过4mm的小高低；二是组织精拨精捣，整治轨向水平复合不平顺病害，消除超高与曲率逆向不平顺和超高与轨向不平顺病害；三是对曲线线路进行精测，利用维修时间对欠超高较大的曲线进行精调。