基于相图几何特征的夹芯梁蒙皮裂纹识别方法

黄雅华，陈建恩*，葛为民，刘 军

(1. 天津理工大学天津市先进机电系统设计与智能控制重点实验室，天津 300384；2. 天津理工大学机电工程国家级实验教学示范中心，天津 300384)

1 引言

裂纹是工程结构最典型的损伤形式，它的出现会影响结构的力学性能，其发展演化更是会为工程结构的安全带来严重隐患和危害。诸如超声波、红外线等局部检测技术，仅适用于静态结构的裂纹检测，对于复杂结构损伤或结构内部损伤，这些检测手段往往无法适用。基于振动特性的整体检测技术通过探测裂纹对结构振动响应的影响识别裂纹位置和深度。相比局部检测技术，该类技术更加高效且具有更强的适应性，此外，基于振动特性的裂纹识别方法可以对裂纹进行实时检测，在不影响工程结构正常运行的情况下完成检测工作。

任何结构都可以看作是由质量、刚度、阻尼所组成的力学系统，裂纹的出现必然会影响结构的振动特性。目前，基于固有频率[1，2]、模态振型[3]、频响函数、柔度矩阵、振动功率流等[4，5]振动信息的裂纹识别方法得到了不同程度的发展，然而，每类方法均存在各自的缺点[6，7]。一些非线性振动特征被逐步用于裂纹识别，这些方法往往可以在裂纹形成前期就可以对其动态特性进行有效的描述，谐波响应是应用最为广泛的非线性损伤指标[8]。此外，基于结构分岔特性、非线性强弱程度及非线性模态的裂纹识别方法也取得了一定的进展[9，10]，但由于非线性问题的复杂性，这些方法在工程应用上仍需进一步开发。理论上讲，任何能够反映裂纹特征的模态参数或振动信号变化都可以用来进行裂纹检测，构建更为丰富的裂纹识别指标，尤其是针对微小裂纹的识别指标，仍是一个重要的研究方向。

点阵夹芯结构[11]是一种在航空航天领域有了一定应用的基础材料，其线性和非线性动力学特性的研究已较为深入[12，13]。Li等[14]利用有限元软件对具有杆件损伤的点阵夹芯板的动力学特性进行了研究。Tian等[15]基于振动信号对点阵夹芯板的蒙皮剥离进行了探测。对于点阵夹芯结构的损伤识别仍是一个亟待解决的问题。

相图是非线性分析中常用的分析手段，包含了丰富的振动信息。相图中的轨道在横坐标上的投影体现了位移的信息，在纵坐标上的投影体现了速度的信息，整个轨道也表示出位移与速度之间的关系。裂纹的出现和演化必然会对相图轨道产生影响，目前，有较多文献利用相图轨道的变化对裂纹参数进行定性分析[16，17]。其中，文献[16]通过分析相图形状随裂纹参数的变化规律，研究了含蒙皮裂纹夹芯梁的振动特性，指出了相图几何特征在裂纹识别方面的潜力，然而在相图特征的定量分析方面仍有待突破。Andreaus 等[18，19]提出利用相图中轨道的偏心率和偏移量差作为损伤指标的裂纹识别方法，使相图信息能够用于裂纹的定量分析，而这两个指标均只用到轨道的位移信息。本文中，对相图的几何特征进行深入的挖掘，提出基于轨道包含面积的裂纹识别方法，并对含蒙皮裂纹点阵夹芯梁的动力学特性进行了分析。

2 裂纹梁的动力学方程

图1(a)为点阵夹芯梁芯层的一个单胞，其中rc表示杆件半径，α表示杆件的倾角，l表示杆件长度。此外，h表示梁的总厚度，hc=lsinα表示芯层的厚度，hf表示蒙皮的厚度。

本文基于Allen的经典夹芯梁理论展开研究[20]。图1(b)为一段含裂纹简支夹芯梁的示意图，蒙皮裂纹位于上面板距离z轴L0的位置，裂纹深度为a，梁长度为L。夹芯梁的等效模型如图1(c)所示，其中μ和m分别表示系统的等效阻尼和等效质量。

图1 含裂纹点阵夹芯梁模型

在振动过程中，等效刚度随裂纹位置和深度的变化而变化，且被描述成一个随时间变化的周期函数，用下式表示

k(t)=ko+kΔC[1+cos(ωt)]

(1)

其中ko为夹芯梁在裂纹完全张开时的等效刚度，kΔC为等效刚度变化的幅度。考虑系统承受简谐激励，获得外激励作用下单自由度含蒙皮裂纹简支点阵夹芯梁的动力学方程为[16]

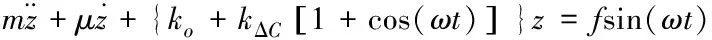
(2)

其中，f为激励幅值，ω为激励频率。对上述方程进行无量纲化处理，获得含蒙皮呼吸裂纹点阵夹芯梁的无量纲动力学方程如下[16]，具体过程详见参考文献。

3 裂纹参数对夹芯梁振动响应的影响

3.1 裂纹参数对夹芯梁相图的影响

取夹芯梁蒙皮和芯层的材料参数及夹芯梁的结构参数为：材料密度ρ=2770kg/m3，弹性模量E=71GPa，泊松比ν=0.33，芯层杆件半径r=1mm，杆件倾斜角α=45°，芯层高度hc=15mm，蒙皮厚度hf=1.5mm，夹芯梁长度方向取25个单胞，单胞的底边长取a=28mm。将芯层等效为连续均匀的材料，其相对密度和等效剪切模量由文献[21]给出。利用龙格库塔法对方程(3)进行数值仿真，取μ=0.2，f=6。采用主共振频率ω=4作为激励频率，将夹芯梁振动的位移与速度看作裂纹位置比(β=Lo/ L)和裂纹深度比(ξ=a / hf)的函数，得到夹芯梁在不同裂纹参数下的相图。

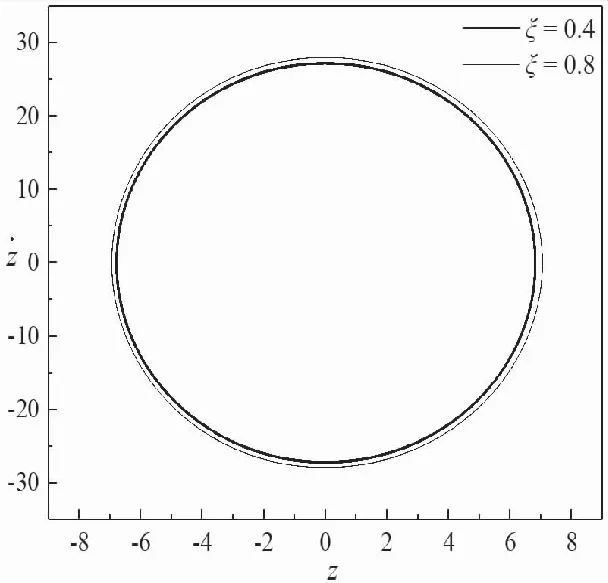
图2 激振频率为ω=4，裂纹位置比为β=0.5时，夹芯梁在不同裂纹深度比下的相图

图2表示裂纹位置比β=0.5时，夹芯梁在不同裂纹深度比下的相图。相图曲线呈较规则的单环形，且裂纹参数的变化必然导致相图面积的变化。在主共振频率激励下，梁的振幅随着裂纹深度的增加而增加。由于相图同时包含了位移和速度的丰富信息，可利用相图的几何特征进行裂纹识别。

3.2 相图的定量分析

本文采取“像素法”计算相图上各闭合曲线的面积。为获得分辨率一致的相图，保持图形中XY轴的区间刻度一致，然后在MATLAB默认窗口截取图像。激振力f=6时将X轴的横坐标区间设为[-8， 8]，Y轴纵坐标区间设为[-30， 30]。保持裂纹深度比或位置比不变，用主共振频率ω=4作为激励频率绘制夹芯梁的相图，在默认成图窗口截取只含X轴、Y轴和相图曲线的图片。

图3 MATLAB对相图的处理过程

图3是MATLAB对相图的处理过程。用MATLAB读取图像，对其进行二值化处理，对封闭区域进行边缘检测，去除边界，对封闭区域标号，并提取各连通封闭区域为白色区域，分别得到相图在各个象限分布的区域如图3(b)所示，计算白色区域的像素。

本文采用主共振激振频率(激振频率ω=4)对夹芯梁进行激励，研究夹芯梁在不同裂纹参数下相图面积的变化情况。

3.2.1 裂纹深度ξ变化对参数η的影响

由图2可以看出随着裂纹深度的变化，相图面积呈现缓慢变化的趋势。并且，具有不同裂纹参数的点阵夹芯梁的相图面积比较接近。为形象描述这种“微小变化量”且使识别指标更具有区分度，本文采用“准标准差”处理相图面积，给出下式

图4 裂纹位置比β=0.4，裂纹深度比和激振力变化对参量η的影响

M表示不含裂纹的相图面积；xn表示裂纹位置比β不变时，裂纹深度比ξ在0.2～0.8范围内变化的相图面积(即x1，x2…x7分别表示ξ=0.2， 0.3， …， 0.8的相图面积)。定义相图面积参量η，该参量表示当裂纹深度比ξ由0.2到0.8变化时，含裂纹相图面积和无裂纹相图面积的差值与准标准差的比值，即

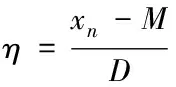
(5)

图4是主共振发生时，在裂纹位置比β=0.4处，激振力f与裂纹深度比ξ的变化对相图面积参量η的影响。图4中可以看出，随着裂纹深度比ξ的增加，η呈逐渐上升趋势；随着激振力的增加，参量η的变化不明显。

3.2.2 裂纹位置β变化对参数η′的影响

x′n表示裂纹深度比ξ不变，裂纹位置比β在0.1～0.5范围内变化时相图的面积(即x′1，x′2， …，x′5分别表示β=0.1， 0.2， …， 0.5的相图面积)，准标准差记为

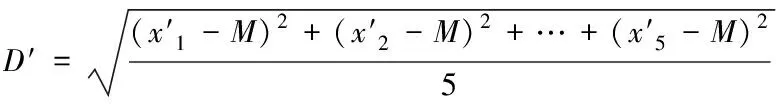
(6)

η′表示当裂纹位置比β由0.1到0.5变化时，含裂纹相图面积和无裂纹相图面积的差值与准标准差的比值，得到下式：

(7)

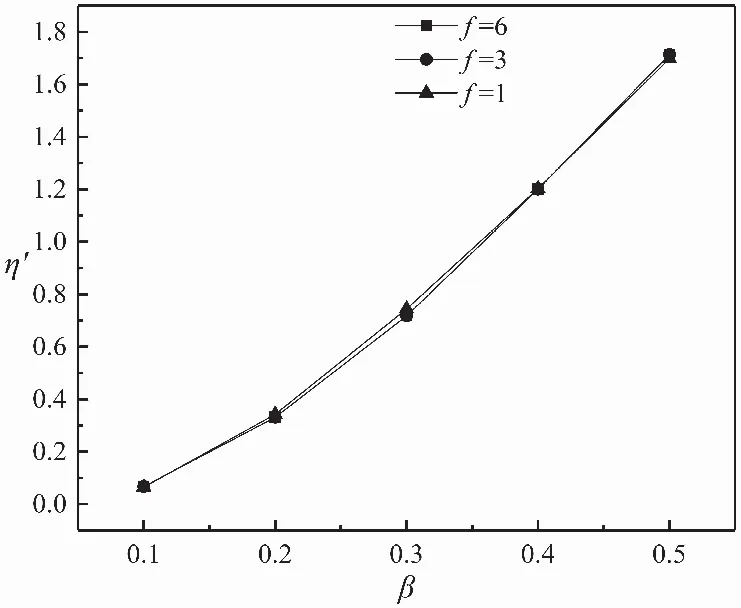
图5 裂纹深度比ξ=0.5时激振力与裂纹位置比的变化对参量η′的影响

图5是主共振发生时，在裂纹深度比ξ=0.5处，激振力与裂纹位置比β的变化对相图面积参量η′的影响。图5中可以看出，随着裂纹位置比β的增加，η′的值逐渐上升；随着激振力的增加，参量η′的变化同样不明显。外力作用对η和η′的影响极小，这有利于利用参量η和η′的关系来识别并确定裂纹参数。

3.2.3 裂纹位置β和裂纹深度ξ同时变化对参量η、η′的影响

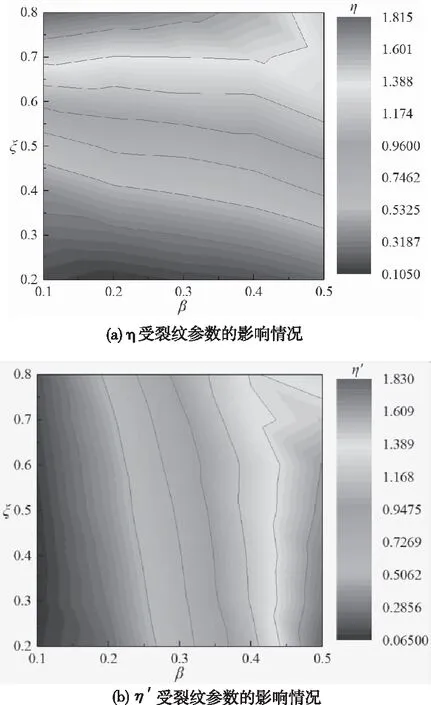
图6 裂纹参数变化对参量η和η′的影响

图6是裂纹参数变化对相图面积参量η和η′的影响。为便于观察参量的数值分布情况，在图6(a)、(b)中标出七条等高线。图6(a)是分别在β=0.1， 0.2， …，0.5的五个裂纹位置上，裂纹深度比ξ在0.2～0.8之间变化得到的参量η的等高线图。例如，在图6(a)中，过β=0.2作垂直于横坐标的辅助线，在该辅助线上，裂纹位置比β=0.2保持不变。可以看到随着裂纹深度比ξ增大，η呈逐渐增加的趋势。图3(b)是分别在ξ=0.2， 0.3， …， 0.8的七个裂纹深度中，裂纹位置比β在0.1～0.5之间变化得到的参量η′的等高线图。例如，在图6(b)中，过ξ=0.4作垂直于纵坐标的辅助线，在该辅助线上裂纹深度比ξ=0.4保持不变。可以看到随着裂纹位置比β增大，η′呈逐渐增加的趋势。等高线的存在表明在相同的η或η′值处会存在不同的裂纹参数，因此需要在相同条件下同时获得一组η和η′值来实现对裂纹参数(位置、深度)的识别。

为了验证该方法的合理性，现选取四种不同的裂纹情况，利用像素法求得不同裂纹参数的相图面积参数η和η′如下表1所示。

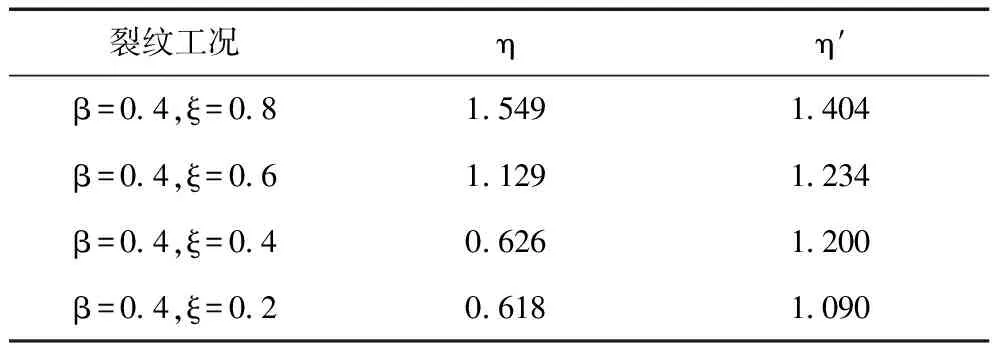
表1 不同裂纹参数下η和η′的值

图7 裂纹参数识别

在图6(a)、(b)上分别找到对应于表1中不同裂纹参数的相图面积参量η和η′的等高线，将η曲线和η′曲线置于同一图中，进而可利用η和η′曲线对裂纹位置比和裂纹深度比进行识别。例如，已知裂纹位置比β=0.4，裂纹深度比ξ=0.8时，η=1.549、η′=1.404，在图6(a)上找到η=1.549的等高线，并在图6(b)上找到η′=1.404的等高线，将η=1.549曲线和η′=1.404曲线置于同一图中，其交点对应的横坐标和纵坐标分别为裂纹位置和深度。同理可得到β=0.4、ξ=0.6， 0.4， 0.2时，η和η′曲线的组合图，如图7所示。故凭借η和η′的数据可以实现对裂纹参数的准确定位。

4 结论

本文提出了利用相图几何特征进行裂纹识别的方法。采用“像素法”获得主共振频率激励下含裂纹与不含裂纹的相图面积，利用“准标准差公式”研究了主共振发生时，夹芯梁在不同激振力作用下，其相图面积受裂纹深度或裂纹位置影响而变化的情况。定义相关的相图面积参量为η和η′。研究结果显示，在裂纹参数相同时，激振力大小对参量η和η′的影响极小。在同一激振频率下，裂纹参数是影响相图面积参量变化的主要因素。

随着裂纹位置或者裂纹深度的增加，参量η和η′都呈现逐渐增大的趋势。参量η的等高线近似水平方向分布，η′的等高线近似竖直方向分布，等高线的存在表明，对于相同的相图面积参量，往往会对应不同的裂纹参数。找到η和η′这两条关系曲线，可以得到与裂纹位置和裂纹深度有关的唯一交点。该方法的识别精度取决于相图面积比的测算精度。

本文通过定量分析相图的几何特征，利用不同参量的等高线交点识别裂纹参数，取得了较为满意的理论结果。该方法还可扩展为提取相图的局部几何特征来识别裂纹参数。但获取“准标准差”的前提是需要获得每组裂纹参数下夹芯梁振动的相图面积，要获得某组裂纹参数对应的等高线交点的前提也是需要预先计算出每组裂纹参数所对应的η和η′数值。换言之，只有预先通过理论计算或实验得到如图6的等高线图，才能进一步对裂纹进行识别。因此，目前本方法仅适用于简单结构的裂纹识别，对于复杂工程结构的裂纹参数识别仍需做进一步的研究。