基于Lasso与禁忌搜索的患者检查需求预测

卿 玥，耿 娜，祝延红

(1. 上海交通大学机械与动力工程学院，上海 200240；2. 上海交通大学中美物流研究院，上海 200030；3. 上海交通大学附属第一人民医院，上海 200080)

1 引言

及时的图像检查对于患者病情诊断和后续手术安排至关重要。准确预测患者需求，有利于图像检查资源的能力分派，减少患者术前等待时间，缩短住院时长，提高病床利用率。

患者需求预测问题，现有研究主要集中在急诊患者需求预测，预测方法可分为线性和非线性方法。大部分相关研究均采用线性预测，常用方法有多元回归分析和时间序列分析。文献[1]发现相较单变量季节Holt-Winters指数平滑法，多变量向量自回归模型在预测急诊患者需求时准确度更高。文献[2]应用基于条件极大似然法的泊松自回归模型预测急诊患者日需求。文献[3]考虑气候、时间因素和患者分类，对比简单季节指数平滑、三次指数平滑、季节自回归差分移动平均(SARIMA)和多元SARIMA四种方法预测急诊患者需求的效果。文献[4]对急诊部门住院患者需求和住院时长进行短期预测，对比了移动平均、简单指数平滑和自回归差分移动平均模型(ARIMA)的预测效果。文献[5]采用ARIMA模型对两类急诊患者需求及其总需求进行预测。文献[6]综述了预测急诊和门诊患者需求的历史文献，对比分析了带有时间变量的回归分析和时间序列模型。

非线性方法以神经网络模型为主。文献[7]应用回归分析和人工神经网络(ANN)对急诊患者需求进行短期、中期和长期预测，发现ANN在中短期预测中占优。文献[8]提出基于ANN的三阶段方法论，用于预测急诊患者日需求并量化预测变量的相对重要程度。文献[9]针对三家不同规模医院的急诊患者日需求预测，分析比较了多元线性回归、SARIMA、指数平滑和ANN多种方法的预测效果。

现有文献对患者需求的研究主要采用单个预测方法进行预测，常用方法各有优劣：多元回归模型和时间序列分析具有技术理论成熟与算法简单等优点，但均基于线性分析，不能准确拟合非线性关系；BP神经网络模型(BPNN)能拟合复杂的非线性关系，但容易陷入过拟合。为综合利用各方法优点并避免单个方法的局限性，很多学者采用组合预测方法进行预测[10]。传统的组合预测方法仅考虑单一的预测性能指标。但预测方法在某一性能指标上表现好，不能就此说明其预测性能好。基于此，有必要同时考虑多个性能指标，并提出有效的预测方法以实现多个性能指标的平衡。另外，检查需求预测与急诊患者需求预测有一定相似性，但检查项目和患者需求的多样性使其受到多种因素影响，导致预测模型的输入变量较多。为减少非关键变量的影响，有必要通过适当的方法，减少预测模型的输入变量。

因此，本文拟引入Lasso方法进行输入变量的降维，基于多元线性回归模型(MLR)[11]、BPNN[8]和多元自回归差分移动平均模型(ARIMAX)[12]等常用的患者需求预测方法进行组合预测，并在此基础上，提出禁忌搜索对组合中的权重进行优化，解决了传统组合预测方法难以同时考虑多个性能指标的问题。

2 基于Lasso降维与禁忌搜索权重优化的组合预测方法

2.1 预测框架

提出的基于Lasso降维与禁忌搜索权重优化的组合预测方法的预测框架如图1所示。数据准备与预处理模块从医院数据中提取历史患者检查需求，并进行数据预处理以保证样本数据的可靠性。Lasso降维模块从候选变量中选择最优输入变量子集，剔除冗余和不相关的变量。然后将最优输入变量子集分别输入MLR、BPNN、ARIMAX和Naïve[13]模型，对所选输入变量与检查需求之间的关系进行建模。最后，用禁忌搜索优化各单预测方法的权重，并基于该权重进行多预测方法组合预测。禁忌搜索算法是邻域搜索方式的一个拓展，由一个初始解开始，在划定的空间内朝着使目标函数值最优的方向进行迭代变换，通过一种动态的记忆结构来设定相应的禁忌准则，避免陷入局部最优[14]。

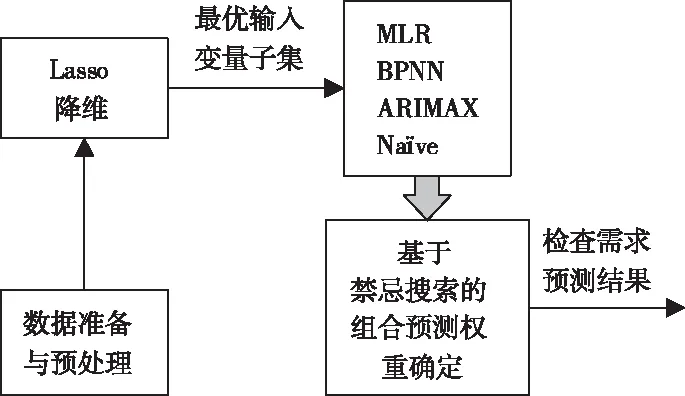
图1 预测框架

2.2 Lasso方法

将与响应变量无关的预测变量作为输入变量，会增加预测模型复杂度、降低模型解释力并导致庞大的计算量。Lasso方法通过系数缩减进行变量选择，能有效降低模型复杂度并显著提高预测准确度[11]。

Lasso的系数β通过求解下式的最小值得到

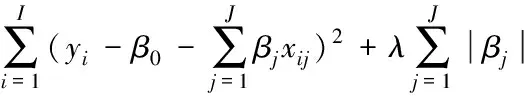
(1)

I为样本观测个数，J为输入变量个数，i用于索引样本观测(从1到I)，j用于索引输入变量(从1到J)，yi表示第i个观测的响应变量值，β0表示所有X为零时Y的均值，βj表示第j个预测变量和响应变量之间的关联，xij表示第i个观测的第j个输入变量值，λ是调节参数(λ≥0)。

式 (1) 中，第一项为残差平方和，与最小二乘法相同；第二项为压缩惩罚，当β1，…，βJ接近零时较小，具有将βj估计值往零的方向进行压缩的作用。调节参数λ，控制这两项对回归系数估计的相对影响程度，综合权衡偏差与方差，通过交叉验证法确定取值。

2.3 基于禁忌搜索的权重优化方法

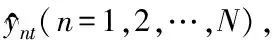
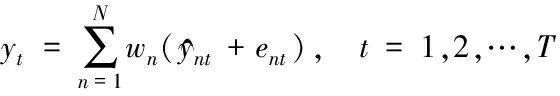
(2)

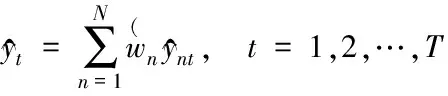
(3)

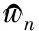
确定每种模型的权重系数是建立组合预测模型的关键。以最小化绝对误差之和为目标的优化问题如下：

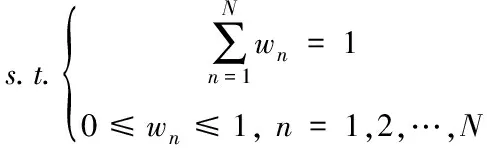
(4)

本文提出了基于禁忌搜索的权重优化方法，以优化训练集的性能指标值为目标函数，为每种预测方法赋予适当的权重以提升预测效果。

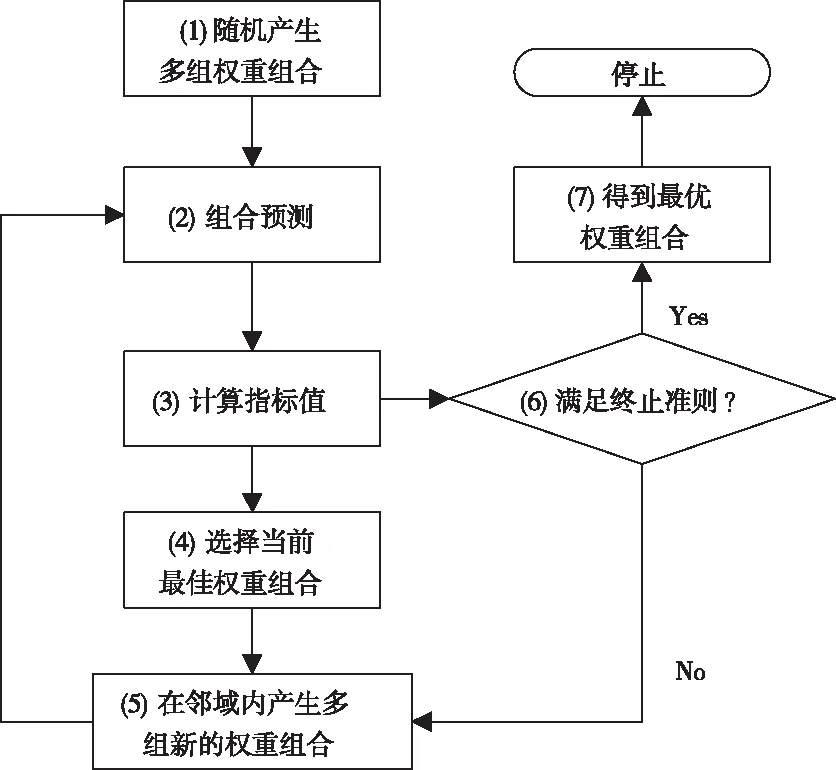
图2 基于禁忌搜索的权重优化流程图

基于禁忌搜索的权重优化方法流程如图2所示。首先设置禁忌表长度、候选解数量、每次迭代保留的最佳候选解个数以及最大迭代步数。主要步骤如下：

1) 随机产生多组权重组合

2) 组合预测

用 1) 产生的权重组合，基于MLR、BPNN、ARIMAX和Naïve四个方法的预测值，得到该组权重组合下的组合预测结果(目标性能指标值)。

3) 计算指标值

计算每个权重组合对应的目标性能指标值。

4) 选择当前最佳权重组合

5) 在邻域内产生多组新的权重组合

将 4) 产生的当前最佳权重组合作为当前解，然后在当前解的邻域中搜索若干候选解，取使得目标性能指标值最优的候选解作为新的当前解。为避免已搜索过的局部最优解的重复，用禁忌表记录已搜索的局部最优解的历史信息。通过特赦准则赦免一些被禁忌的较好解，从而保证多样化的有效搜索。

6) 算法终止准则

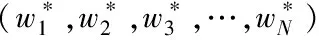
3 数值实验

3.1 实验设计

3.1.1 数据预处理

本文基于上海某三甲综合医院2014年1月1日到2014年12月31日的住院患者检查需求数据，考虑CT、磁共振和彩超三种图像检查，将患者分为七类，如表1所示。预测模型均采用10折交叉验证进行数据重抽样。

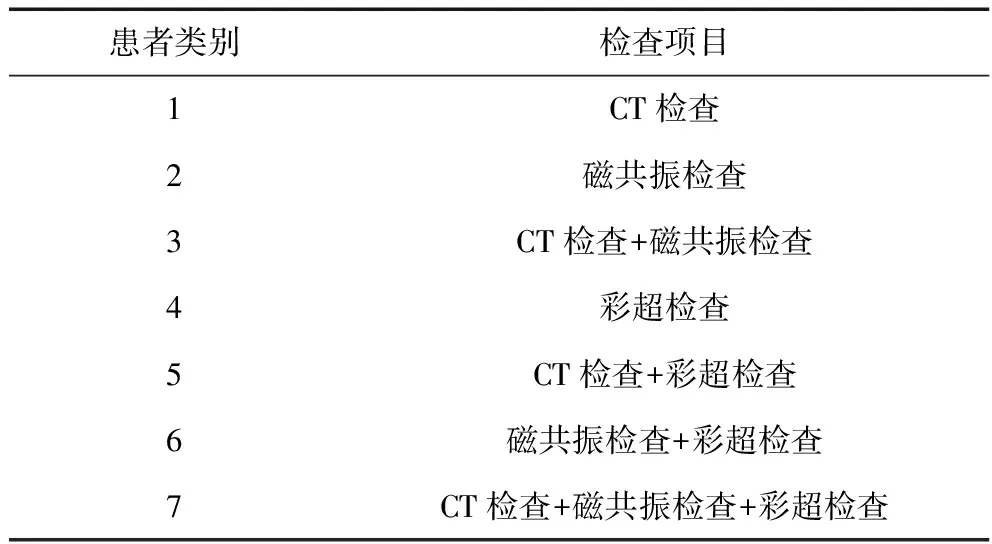
表1 患者分类

实验数据集时间范围为2014年1月1日到12月31日，共365天，无缺失值。由于检查科室在节假日只接收急诊患者，故节假日需求作为异常值被剔除。实验采用最小-最大归一化方法[16]统一输入变量的数据范围。

3.1.2 性能指标

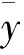
1) 决定系数(R2)

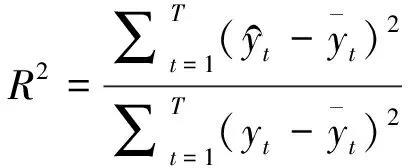
(5)

2) 平均绝对百分误差(MAPE)

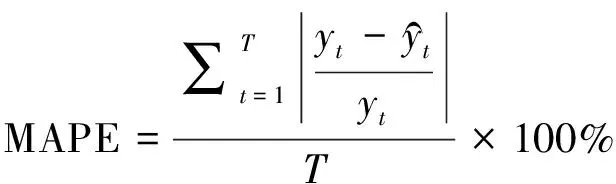
(6)

3) 均方根误差(RMSE)

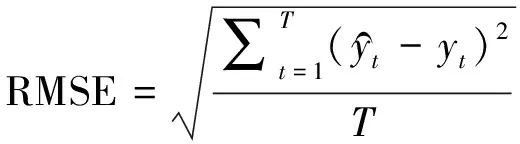
(7)

3.1.3 影响图像检查需求的候选输入变量选择

结合相关文献、数据可得性和对检查科室医务人员的访谈，选择时间、气候和检查需求量相关的30个候选变量如表2所示。针对每类患者的需求数据，应用Lasso方法从候选变量中选取对检查需求有重要影响的输入变量。七类患者检查需求的降维结果详见附录A。

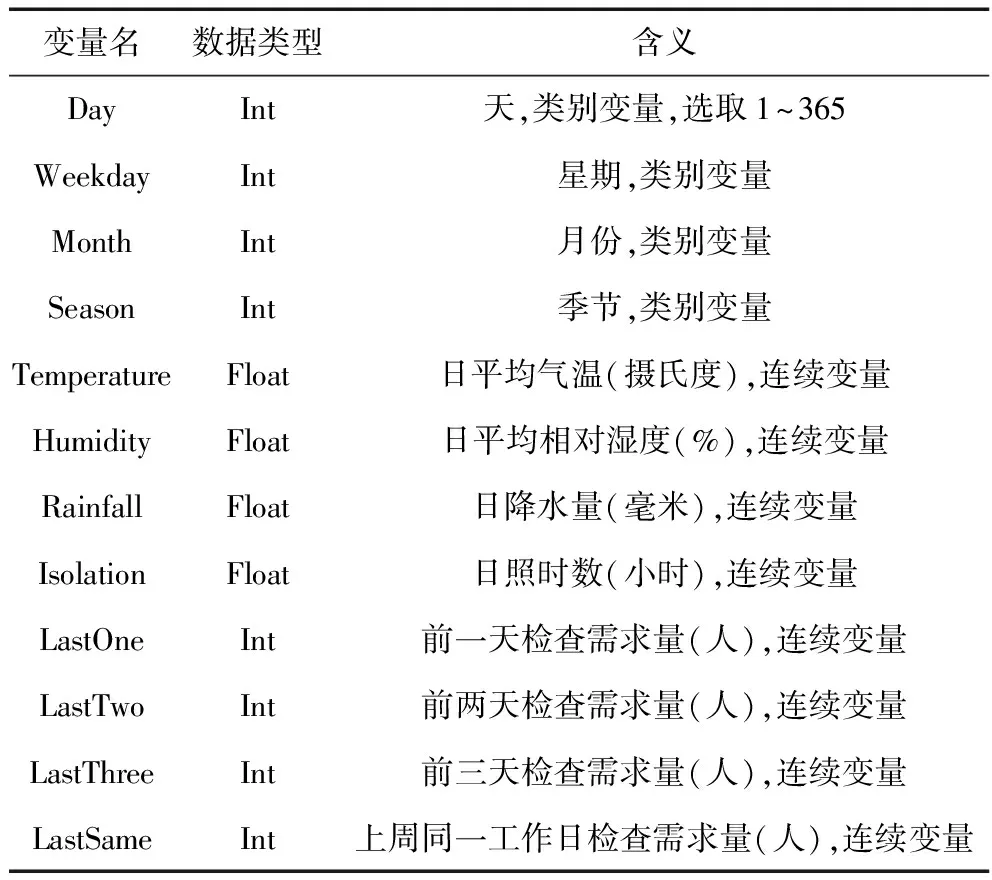
表2 候选变量

3.1.4 参数设置

禁忌搜索算法中，禁忌表长度选取10，邻域中的候选解数量为15，每次迭代保留10个最佳候选解，最大迭代步数设置为30(经实验观测，此设定可使算法收敛)。

三层神经网络具有良好的逼近性能[17]，故本文采用三层BPNN。用试错法确定最优的隐藏层神经元个数。

根据自相关和偏自相关函数图，通过试错法确定ARIMAX模型的参数值：差分次数d，自回归项阶数p以及移动平均项阶数q。

假定患者检查需求呈星期规律，Naïve方法即为预测日的检查需求量等于上周相同工作日的历史检查需求量。

3.2 实验

3.2.1 实验1：组合方法与单方法的预测性能比较

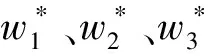
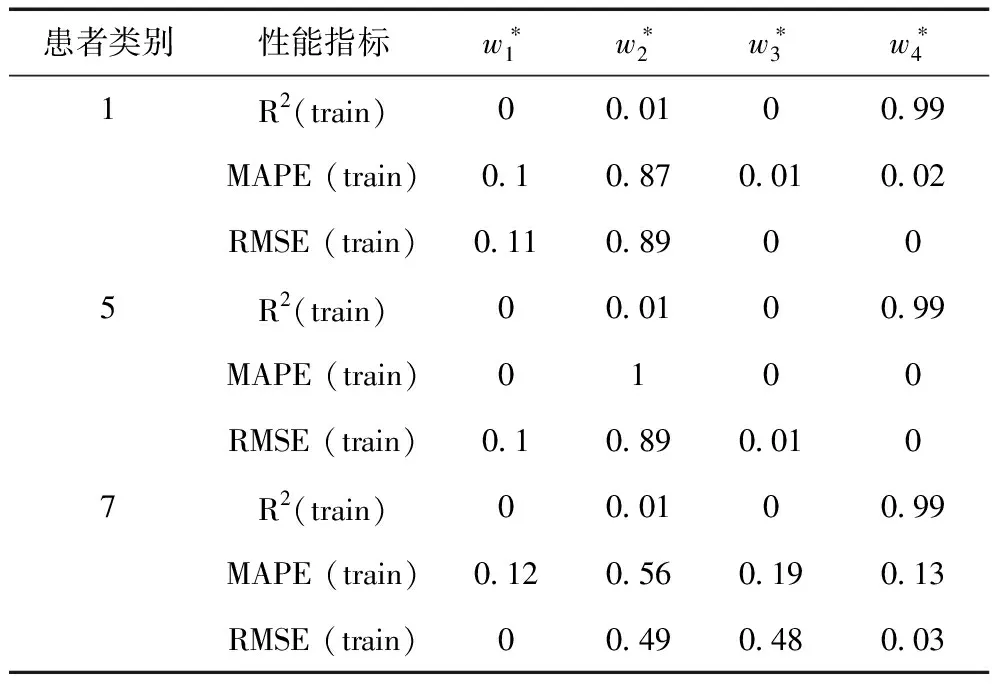
表3 最优权重组合

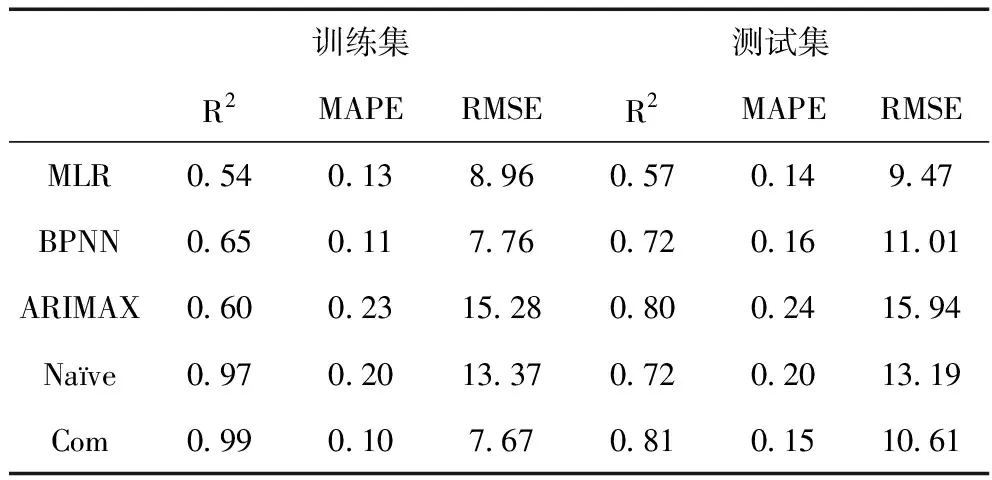
表4 第1类患者预测性能对比

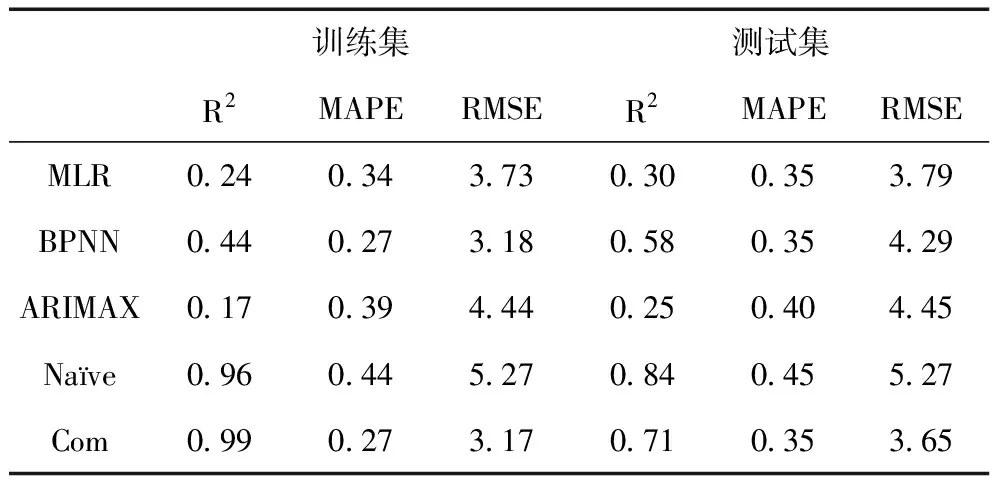
表5 第5类患者预测性能对比

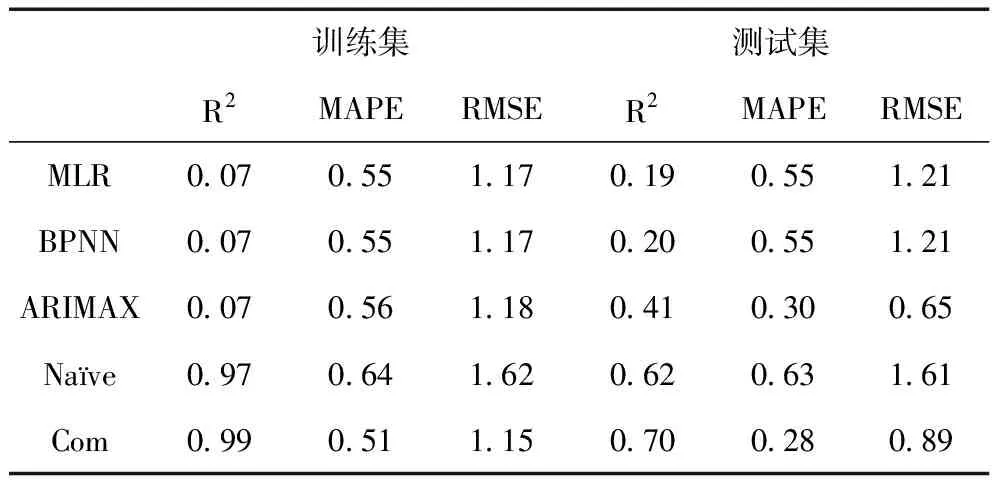
表6 第7类患者预测性能对比

基于七类患者检查需求的预测结果，图3进一步对比了组合方法和四种方法的性能。柱形条表示对应预测模型根据特定性能指标生成的最优指标值的患者类型数量。以组合方法(Com)为例，其对应的R2(test) 柱形条表示组合方法在5类患者需求数据的测试集的R2指标值比MLR、BPNN、ARIMAX和Naïve方法更优。

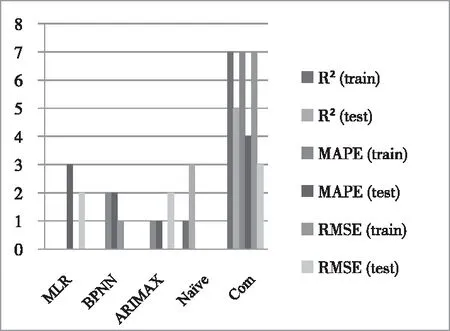
图3 组合方法与单方法性能比较

结合预测结果，组合方法的R2、MAPE和RMSE指标值优于单方法或接近最佳取值。例如，表4所示第1类患者需求预测结果，组合方法在训练集的R2指标值比单方法改善了2%及以上，在测试集的R2指标值和训练集的RMSE指标值改善了1%及以上，在训练集的MAPE指标值改善了9%及以上，而测试集的MAPE指标值0.15与其最佳取值0.14接近、测试集的RMSE指标值10.61与其最佳取值9.47接近。由此可见，本文所提组合预测方法综合了四种方法的优势，实现了R2、MAPE和RMSE三个性能指标的平衡，预测性能优于单方法预测。

3.2.2 实验2：禁忌搜索与Lasso降维对预测性能的影响

为进一步验证本文提出的组合预测方法的性能，以第1类患者检查需求数据为例，运用传统的权重组合预测方法[15]进行预测，两种组合方法的预测性能对比如表7所示，Com*行表示传统线性加权组合预测方法。两种组合方法的MAPE和RMSE指标值接近，而本文所提组合预测方法在训练集和测试集的R2指标值分别改善了52%和53%。由于传统线性加权组合预测方法是以最小化绝对误差之和为单一目标，不难理解其预测结果会在与优化目标高度相关的指标MAPE和RMSE上表现较好，而在R2指标的效果差。本文所提出的组合预测方法，考虑了多个性能指标的平衡，能同时优化R2、MAPE和RMSE三个指标，提升了预测精度。

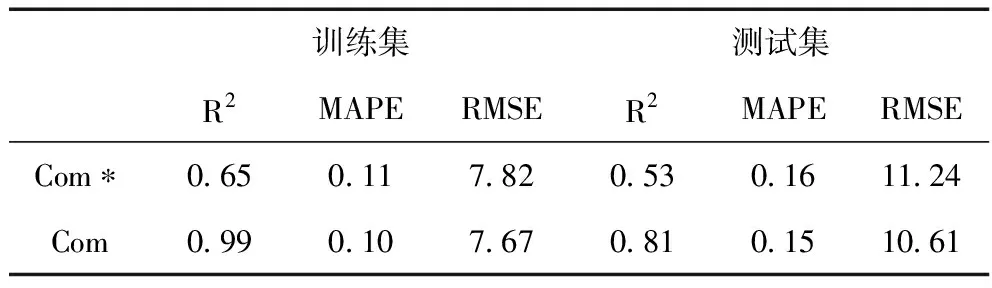
表7 两种组合方法预测性能对比

基于第1类患者检查需求数据，表8所示，星号行(*)表示未进行Lasso降维的模型预测结果，其余行表示采用Lasso降维后的结果。以测试集的三个指标为例，R2改善了至少5%，MAPE改善了4%～26%，RMSE改善了3%～19%。Lasso降维后，无论是单方法还是本文所提出的组合预测方法，在R2、MAPE和RMSE指标的预测性能均优于未降维的结果。

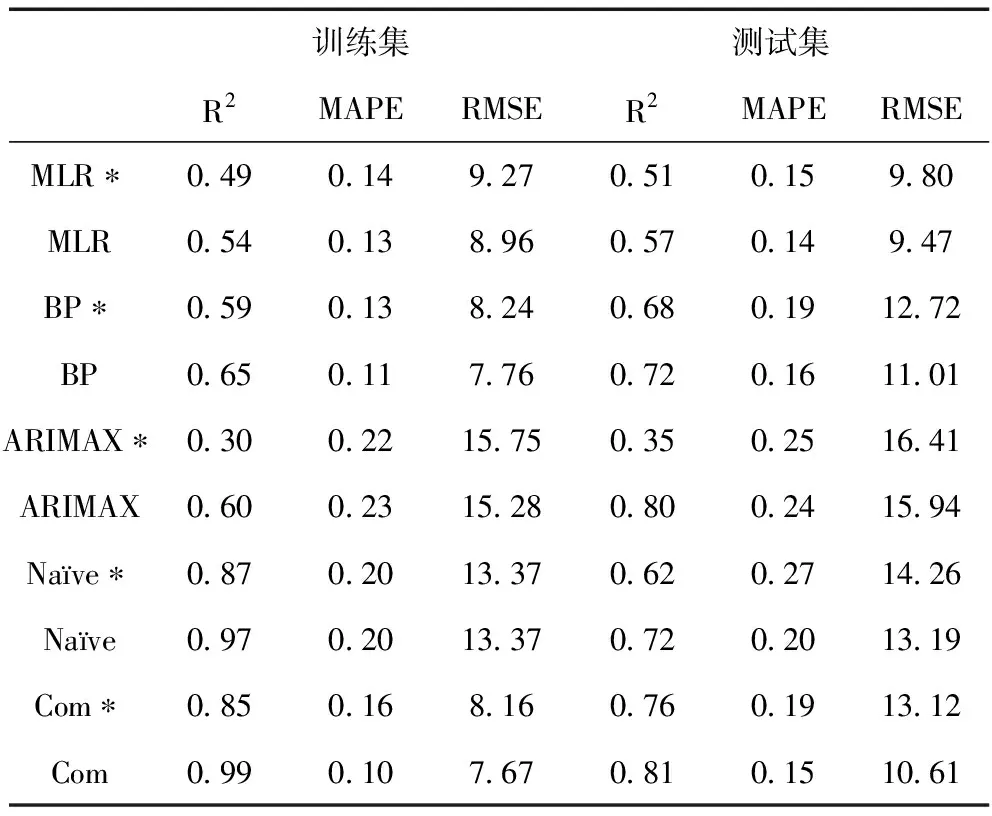
表8 Lasso降维对预测性能的影响

4 结论

本文针对住院患者图像检查的多需求预测问题，采用Lasso降维筛选输入变量，结合常用患者需求预测模型提出组合预测方法进行预测。实验结果表明，该组合方法吸收了单模型的优点，综合考虑了多个性能指标的平衡，在R2、MAPE和RMSE三个指标上，预测性能相比单模型预测有所提升，并验证了禁忌搜索与Lasso降维能有效改善预测精度。基于本文对图像检查需求的预测结果，可进一步研究检查设备的能力分派与患者调度。