基于支持向量机的复杂地质分形特征自动提取
2021-11-18张钰帆王艳霞
张钰帆,郑 寒,王艳霞
(西南林业大学,云南 昆明 650224)
1 引言
地质复杂程度主要是某一地区水文、矿产、构造、岩相、岩性以及地层等各种地质内容变化的程度。相对的来说,变化较小的简单、变化较大的复杂,介于两者间视为中等。它是影响地质工作方法的选取、效率以及工作量大小等重要因素,同样也是制定地质工作计划的依据之一[1]。其中地质复杂程度主要是指工作区域中,各种各样的地质条件以及地质状况总称,例如:地质特征是否明显、断裂构造是否发育,地层的变化是否频繁等。通常来说,地质情况越复杂,所需要的观察点就多一些,相反就会少一些,对应的效率会造成一定影响。而地质复杂的程度与自然地理条件是影响地质测量工作效率两个主要因素,在制订劳动定额时,需要先对两个因素进行分类,反之,即会使劳动定额缺失准确性,影响劳动定额生产、调动职工的劳动积极性。为此,相关学者进行了研究,取得了一定的进展。张雁等人提出基于地质成因的砂岩储层微观孔隙结构分形特征分析方法[2],通过扫描电镜等对松辽盆地大庆长垣渗透性砂岩储层微观分形特征进行分析,通过成岩作用以及次生孔隙的发育情况研究地质成因,此方法能够有效实现地质分形特征的提取,但是精准性不佳。张鹏等人对黔西北地区龙潭组海陆过渡相泥页岩孔隙分形特征进行研究[3],通过FHH模型获取页岩孔隙分形维数,分析页岩其它地质参数与分形维数的相关性,得到其分析特征结果。此方法能够获得较为全面的地质特征,但是勘探工作效率较低。
为了解决上述方法中存在的问题,精确的找出某种物质,本文提出一种基于支持向量机的复杂地质分形特征自动提取方法,能够很好的区分出泥岩性质,完成地质勘探工作。
2 支持向量机下分类平面获取
2.1 最佳分类平面
先考虑最简易两种线性可分,把最佳的分类面完成简化,将其转变成最佳分类直线。具体如图1所示。
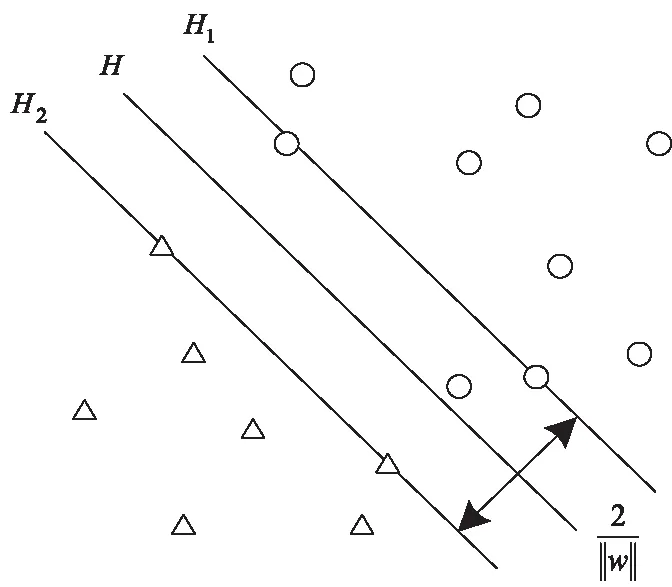
图1 最佳分类平面
通过图1能够看出,○与Δ分别表示两种可分的训练样本,而H分类面就是把两种样本精确无误分开,分成H1,H2使二者分别代表两种样本内离H最近的点,并且要平行于H平面。将H1与H2间距离称之为两种分类间隔。最佳分类面不仅要确保两种标本无错分开,且还要让分类的距离达到最大。主要是前者可以确保经验风险达至最低,不过后者会致使推广性界置信的范围达到最低,即为真实的风险达到最低[4]。
线性可分样本的集主要为n个样本(xi,yi),其中i=1,2,…,n,x∈Rd,y∈{-1,1}代表类别标号。而处在高维的空间内,分开两种样本的分类超平面需要满足g(x)=w·x-b=0。利用归一化处理向量系数w,能够致使全部的样本满足|g(x)|≥1,所以图1内H1与H2分别要满足公式为
H1:w·x-b=+1
(1)
H2:w·x-b=-1
(2)
将式(1)、(2)总结,全部样本的精准分类公式为
yi(w·xi-b)-1≥0
(3)
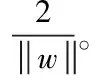
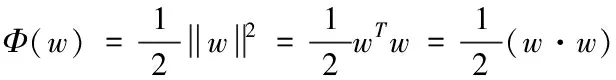
(4)
风险最小就是指求解最佳的分类面处于式(3)约束时,能够求出式(4)内Φ(w)极值。而超平面H1与H2样本点即为式(9)内所获的极值样本点,同时支持最佳的分类面,因此将其称之为支持向量[5]。
而为了对上述问题解答,需要对w与b采用最小化的Lagrange泛函数,具体公式可以得到
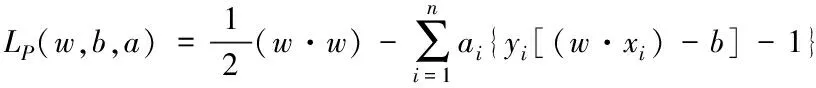
(5)
式中:σi>0,i=1,2,…,n为引入Lagrange的系数,经过约束优化理论条件,在式(5)内的极值问题可以简化成对偶的问题,具体公式为
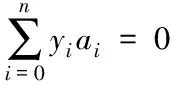
(6)
σi≥0i=1,2,…,n
(7)
而下极大化的泛函公式为
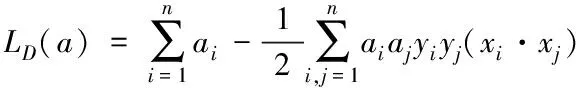
(8)
通过KT条件能够看出,不等式约束条件下,二次函数的极值拥有唯一的解答,具体最佳公式为
ai[yi(w·xi-b)-1],i=1,2,…,n
(9)
式中:σi≥0相应的样本xi现实中即为支持向量,a′代表优化的最佳解,具体通过可以通过式(8),得到最佳平面系数的向量公式为
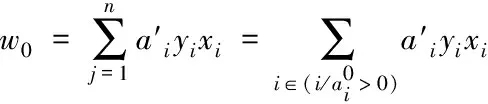
(10)
基于最佳超平面分类规则,能够利用下列指示函数进行表述,具体公式为
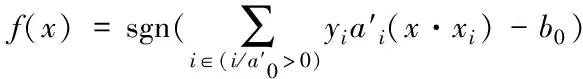
(11)
而常数b0能够通过式(9)在两种样本内获得随意的一个支持向量[6]。
2.2 广义最佳分类面
真实的情况内,在对噪声或其它的干扰因素所造成的线性不可分问题进行考虑,不能够按照要求令样本落在图1内H1与H2超平面间,在引入参量ξi≥0,则式(8)内约束的条件能够推广成公式为
yi(w·xi-b)-1+ξi≥0,i=1,2,…,n
(12)
广义最佳超平面的解决问题,即为在条件式(12)与ξi≥0,i=1,2,…,n约束下极小化的泛函数,具体公式为
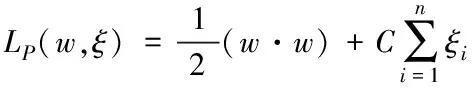
(13)
式中:常量C可以对越界的样本点施加惩罚系数,即而在算法复杂度以及样本错分率间进行折中,在C→∞时,即可以成为最优分类理想的状况[7]。
和以上解决方式相同,式(13)的转变形式与式(8)同样的对偶问题,具体将约束条件转换成公式为
0≤ai≤C,i=1,2,…,n
(14)
2.3 非线性可分下高维空间映射
讨论线性超平面以及推广形式,说明最佳的分类判别函数在式(11)内,仅包括待预测的样本以及支持向量间内积,通常需要考虑分类的问题处于定义特征的空间内,并不一定是线性可分的,因此采用非线性的映射T把特征x映射到高维线性特征空间F内,具体公式为
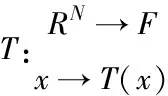
(15)
接着利用之前所介绍的广义最佳分类面方法进行解决,而高维线性空间内积公式为
K(xi,xj):=T(xi)·T(xj)
(16)
式中:K(xi,xj)代表核函数,选取要满足的Mercer条件。
上述支持向量机的优点,是无须知道必要映射的T具体形式,只需要定义高维空间内积的运算K(x,y)即可完成,这样就算是经过变换之后,空间维数同样会增加许多,不过复杂度的计算也并没有较大变化[8]。
3 复杂地质分形特征自动提取
3.1 分数布朗运动法
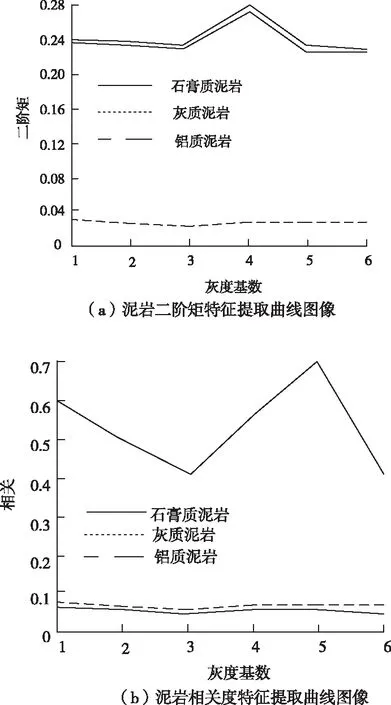
假设x∈En(En为n维的欧式空间),f(x)为关于x实值的随机函数,如果具有常数H(0 (17) 式中:F(t)为一个和x·Δx没有关系的分布函数,那么f(x)将称为分维布朗函数。 如果F(t)的服从均值是0,方差则为σ正态分布,那么实际的布朗噪声具体公式为 (18) 将式(18)两边取对数,那么可以得到公式为 (19) D=3-H (20) 式中:D代表分维数。 抽取异常重磁分维数方法如下: E[|f(X+ΔX)-f(x)|]→E[i](i=1,2,…,k) (21) 其中 (22) 2)对式(19)采用最小二乘法,算出H与lgC结果。 通过频率域角度观看分维值,能够反映出不同频率能量关系,例如从低频向着高频的能量衰弱。在从空间域角度观看,分维数能反映出目标区域地形复杂程度,非常直观的表示表面粗糙程度,D越大,则表面的起伏就越剧烈,且相关程度就越低。D越小,则表面变化就越缓慢,而相关程度就越高。 选择需要两部分复杂地质图像样本,计算图像内的方差、均值、相关性、对比度以及角二阶矩。 L代表灰度级的个数,P(m,n)代表共生矩阵第m行和第n列元素值,其主要是以灰度级m作为起点,生成灰度级n概率。 具体角二阶矩公式为 (23) 对比度公式为 (24) 式中,t代表灰度级。 而相关性G公式为: (25) (26) (27) (28) (29) 式中:μ1,μ2代表均值,σ1,σ2代表方差。 均值E计算公式为 (30) 方差σ计算公式为 (31) 式中:μ代表P(m,n)均值。建立特征子向量P1=[β,α,G,E,σ]。 分解两部分的样品图像尺度是3,计算各个尺度低频系数图像的方差、均值、相关性、对比度以及角二阶矩。建立特征子向量P2=[βLL(i),αLL(i),GLL(i),ELL(i),σLL(i)]i=1,2,3,其中:βLL(i)、αLL(i)、GLL(i)、ELL(i)、σLL(i)分别代表分解尺度是i时LL子带的方差、均值、相关性、对比度以及角二阶矩。 而HH子带系数的均值公式为 (32) 式中:HH(i)代表分解尺度值是i时的子带HH,m代表系数的行数,n代表系数的列数,M代表总系数的行数,N代表总系数的列数。而其它子带的系数均值能够利用类似方法计算。经过分解以后各个分解尺度均值公式为 (33) (34) 其它子带系数的方差能够利用类似方法进行计算。 经过分解以后,各个分解尺度总方差公式为 (35) 建立特征子向量P3=[μ(i),σ(i)]i=1,2,3,构建纹理特征向量P=[P1,P2,P3]。即完成复杂地质特征提取工作。 图像收集系统采用Canon EOS 20D照相机,配上Canon Macro MP-E65mmf/2.81-5X微距镜头。在进行实际拍摄的过程内,镜头至岩屑距离8cm,避免出现过多阴影。实验样品采用《岩谱色谱集》内铝土质泥岩、石膏质泥岩、灰质泥岩一共3种泥岩样品,将粉砂岩、灰质粉砂岩、粉细砂岩、中砂岩以及石英砂岩5种作统一砂岩样品。 将拍摄的复杂土质样品图像,截取整幅正方形大小为128×128的小图像。泥岩标准图像样品取样为120幅,实际现场截取样品为200幅,砂岩标准图像样品截取110幅,实际现场截取样品为300幅。 通过计算4种纹理特征向量,获取3种泥岩表面纹理,仅以两种特征向量进行举例,具体如图2所示。 图2 泥岩的特征向量提取曲线图像 通过图2能够看出,不同类型的泥岩表面纹理特征数据存在显著差异,因为这些参量代表图像纹理特征的某一个方面性质,所以利用对比这些参量,能够反映出不同图像的纹理特征差异,因此把作为分类器输入的特征矢量,分类识别泥岩表面的纹理是可行的,能够完成对不同泥岩分类。 而在图2(a)内,曲线表示各个泥岩二阶距的特征,数值越大,则说明纹理就越粗,即为能量越大,图内表示铝土质泥岩与石膏质泥岩两条曲线的差距较大,因为铝土质泥岩的值要比石膏质泥岩大很多,这就说明铝土质泥岩的纹理要比石膏质泥岩纹理粗,即能量也大,以此就能够利用二阶矩区分开两种泥土种类。不过其中表示灰质泥岩与石膏质泥岩二阶矩曲线互相重叠,很难分辨。所以这时需要看图2(b)中,在图内曲线表示各个泥岩纹理对比度特征,其中表示石膏质泥岩与灰质泥岩对比度曲线差距比较大,因为灰质泥岩值要比石膏质泥岩值大许多,所以就表示灰质泥岩值要比石膏质泥岩纹理清晰许多,这时就能够区分开灰质泥岩值与石膏质泥岩,以此类推,本文方法能够通过提取的特征值轻松区分出3种泥岩。 本文提出的基于支持向量机的复杂地质分形特征自动提取方法,能够很好通过提取出的特征,区分各种泥岩,不过因为复杂地质中的存在较多种泥岩,部分泥岩的成分较为相似,可能会存在提取出的泥岩特征用于识别或分类时出现差错,导致最终结果偏移,影响勘探工作,所以未来本文需要进一步研究,提升地质特征提取的精度,尽可能的减少提取时误差。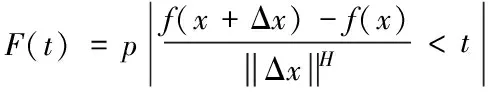
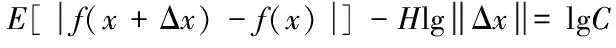
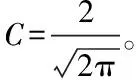
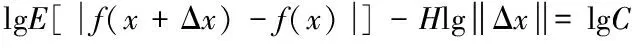
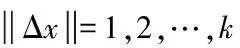
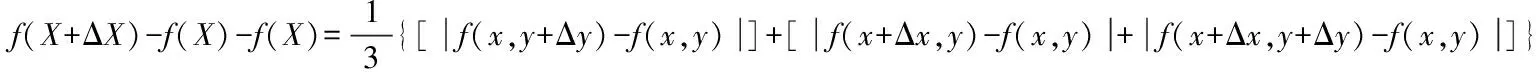
3.2 复杂地质特征提取
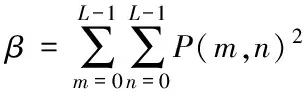
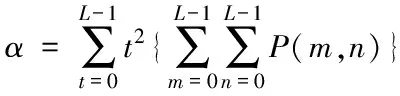
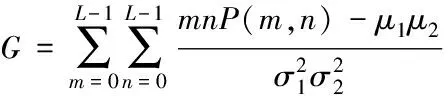
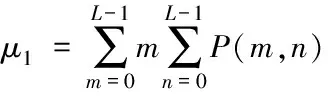
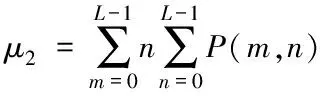
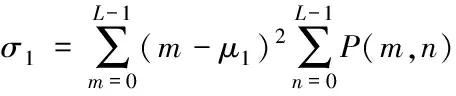


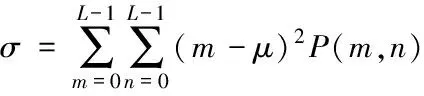
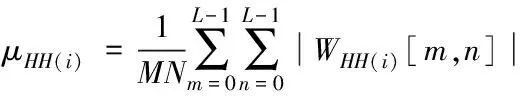
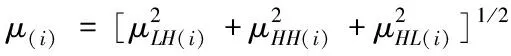
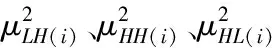
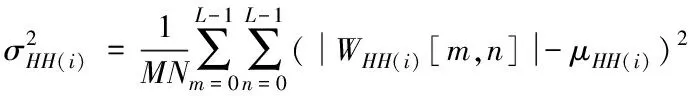
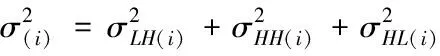
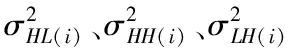
4 实验证明
4.1 实验环境
4.2 实验结果与分析
5 结束语
