基于余数系统蒙哥马利模乘器的RSA密码算法
2021-11-18程雨芊李智超
程雨芊,李智超
(山东大学(威海),山东 威海 264209)
1 引言
随着计算机网络技术的高速发展,社会信息化程度日益提升,使得网络信息的开放性与共享性更容易受到不安全因素的威胁,从而导致国家与社会领域中的动态信息和个人信息被泄露、窃取,所以信息安全问题引起了相关领域的广泛关注。作为信息安全领域的有力工具,密码技术不仅能够确保信息的安全性与完整性,还可以实现身份验证,提高系统安全性能[1]。密码技术凭借其安全保密功能与普遍应用性,具有更宽广的应用空间。二十世纪末期的三位著名密码学者创建了一种基于大数因子分解困难性的公开密钥密码,即RSA密码,作为当今最具影响力的公钥加密算法,RSA除了加密功能之外,还可以用来完成数字签名,所以该算法已经成为应用最为广泛的公开密钥密码之一。
文献[2]为了更好地观测到RSA的加密过程,将旁路电磁轨迹特征作为加密对象,对模板进行创建,通过识别未知测试轨迹中的加密操作,再与密钥相结合,得到密钥序列,经过分析移动设备PCM-9589F凌动主板的电磁旁路,构建一种旁路信号采集平台,利用提取到的RSA加密算法二进制密钥序列,完成密钥破解与算法设计。文献[3]针对海洋信息观测与无线组网安全通信需求,设计一种融合了AES算法、RSA算法以及消息认证码的一次性双向口令认证协议,通过评估RSA算法,改进算法流程,使资源消耗得到减少,从而提高通信安全。
由于上述文献中的RSA算法无法通过大位宽乘法实现模乘运算,因此本文设计出一种基于余数系统蒙哥马利模乘器的RSA密码算法。采用一组两两互素的整数对余数系统进行界定,并将余数系统的表示形式转变成常用的二进制数值表示形式,根据双模式乘法器与硬件平台创建模乘器,其输入端的初始操作是由系统总线传输,在主路选器上连接所有模乘器的输出端,确保下一周期的正常运转,经过嵌入ROM以便储存预计算数据。利用引入的蒙哥马利模乘来去除取模阶段的除法运算形式,从而改写余数系统转二进制数值的运算方式,以取模阶段中的参数为基础,运用一种近似方法的移位操作替换除法运算,并采用修整因子对产生的误差进行修正,使用barret约减算法完成模乘与模乘累加的取模操作,最后经过将大数分解成小数部分,令RSA密码算法得以实现。
2 余数系统蒙哥马利模乘器设计
因为余数系统(residue number system,简称RNS)具有高速、并行的模计算性能,通过一组互质的余数系统基[4],便能够将其分解为一个较大规模的数,从而利用一组小数完成并行计算,所以有效结合余数系统与蒙哥马利模乘,可以进一步使模乘运算效率得到提升,实现并行挖掘。
作为并行数值表征系统的余数系统,与一般系统相比,所有分量间均相对独立、并行,且没有进位。余数系统的界定方式为一组两两互素的整数,而余数系统的基则是该组互素整数集合[5]。假设B=(m1,m2,…,mk)为一个余数系统的基,故采用下列表达式来描述任意整数X
[X]RNS=(x1,x2,…xk)
(1)
式中,xi=Xmodmi。
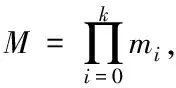
若想将余数系统的表示形式转变成常用的二进制数值表示形式,则需要通过下列公式达成
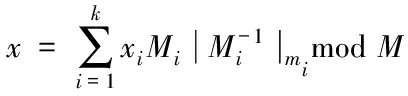
(2)
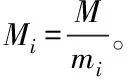
设定余数系统的a、b表示是a=(a1,a2,…,ak)与b=(b1,b2,…,bk),则利用下列表达式对其加、减以及乘运算法则进行描述
a⊗b=(|a1⊗b1|m1,|a2⊗b2|m2,…,|ak⊗bk|mk)
(3)
式中,⊗=(+,-,×)。
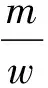
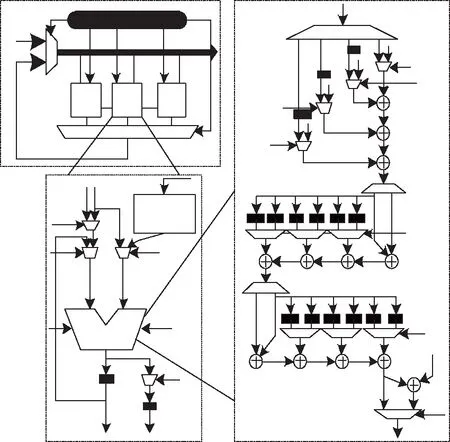
图1 余数系统蒙哥马利模乘器框架示意图
通过四状态下有限状态机的调度控制器对模乘器进行控制[6],系统总线将原始操作数据输送至模乘器的输入端,并在主路选器上连接全部模乘器的输出端,为总线入口挑选合适数据,确保下一周期硬件能够正常运转,而各模乘器间的数据通路则是为了基扩展的中间数据共享。
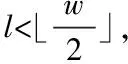
模乘器的核心模块是算术逻辑单元[7],用于完成乘法与乘累加运算,该模乘器的输入源分为三种:系统总线输入、存储于片内ROM的预计算数据以及算术逻辑单元的输出端数据。
基于余数系统的蒙哥马利模乘器储存空间如下表所示。

表1 余数系统蒙哥马利模乘器储存空间统计表
算术逻辑单元的构成部分为异或门与选通器,部分积累加器为其主要部分,用于计算多项式乘法,基本原理如下式所示
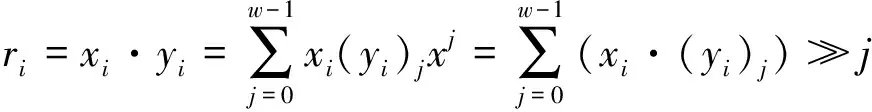
(4)
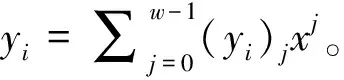
积累加器的加法器主要用于实现累加运算,维持其正常工作的前提条件是乘累加模式为启动状态。
3 RSA密码算法设计
由于余数系统中的运算式(3)无法完成并行化的除法运算[8],故引入蒙哥马利模乘来去除取模阶段的除法运算形式,进而对算法流程进行调整。
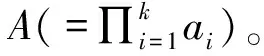
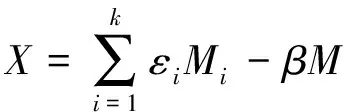
(5)
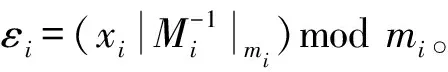
把M取模时所需的参数β引入上式,能够得到下列表达式
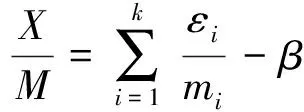
(6)
为了使硬件部分设计顺利完成,采取一种近似方法,将εi近似为高g位,mi近似为2r,从而推导出下列表达式
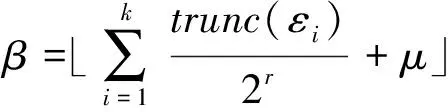
(7)
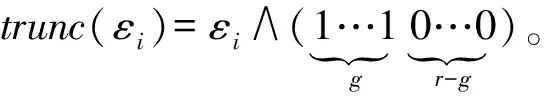
利用该近似方法对移位操作进行除法运算,使硬件架构复杂度下降,并采用修整因子对产生的误差进行修正。
通过二进制位扫描模幂算法对数据进行预处理,将数表示形式转变为蒙哥马利域的表示形式,按照幂指数有效位从高到低的顺序进行扫描,迭代次数为n,该值同时也表示幂指数的二进制比特位数。因为RSA协处理器的汇编代码控制整个循环阶段,因此能够实现不同密钥长度循环,因此该阶段为密码协处理器优化的重要阶段之一。
根据余数系统蒙哥马利模乘器中的数据依赖关系,构建RSA密码算法执行的预估时间公式
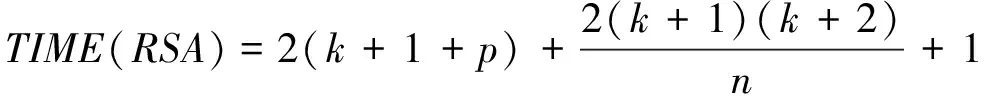
(8)
采用上列公式设定各单元数量,进而分析算法性能与芯片面积的关系,令不同的使用需求得到满足。
作为RSA密码算法的关键运算形式,模乘与模乘累加的取模操作可以通过barret约减算法的加法、乘法与移位实现。假设操作数的长度为z,下列公式即为barret约减算法操作复杂度的表示形式:
COMPLEXITY(barret)=2z2M+S+eA+kS+4T
(9)
其中,e取值为0或1,k≥0。两个n比特的数相乘为n2M,减法、加法以及移位操作分别是S、A和T。由于乘法的次数与乘数位数决定了其复杂程度,因此,硬件实现复杂度的最具代表项为2n2M。
设定基为一种特殊形式2n-ci,其中ci为一个较小的数,n则表示基的二进制比特位数,该形式的基不仅能够降低模乘复杂度,而且可以实现基的高效选取,究其原因是该形式基的模加运算只需执行两次加法运算即可完成,采取移位操作就可以实现其除法与取模操作。因此,采用下列公式对该形式基的整个取模操作复杂度进行描述:
COMPLEXITY(base)=ntM+ttM+3A+5T
(10)
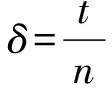
COMPLEXITY(base)=(δ2+δ)n2M+3A+5T
<0.75n2M+3A+5T
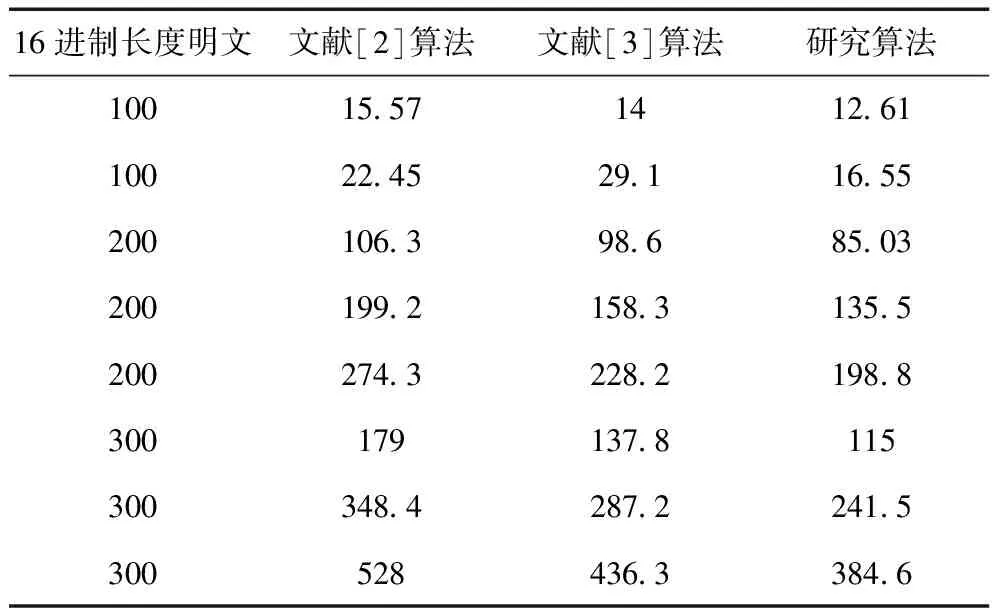
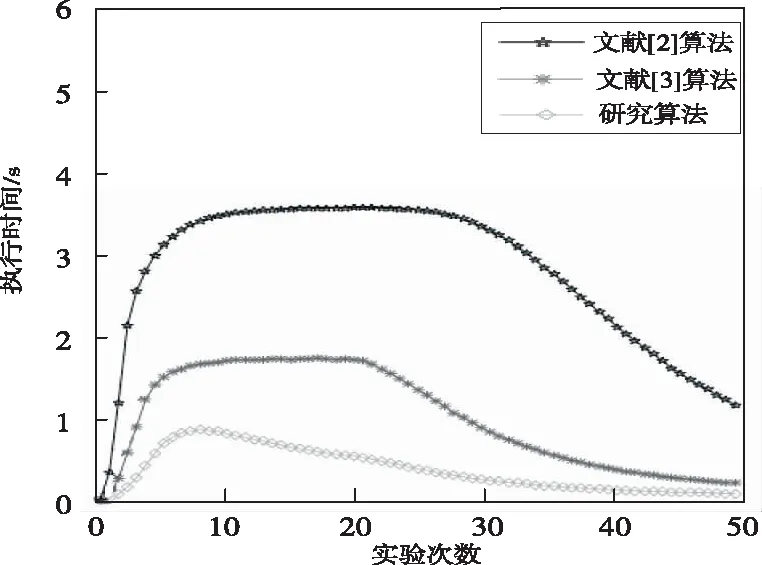
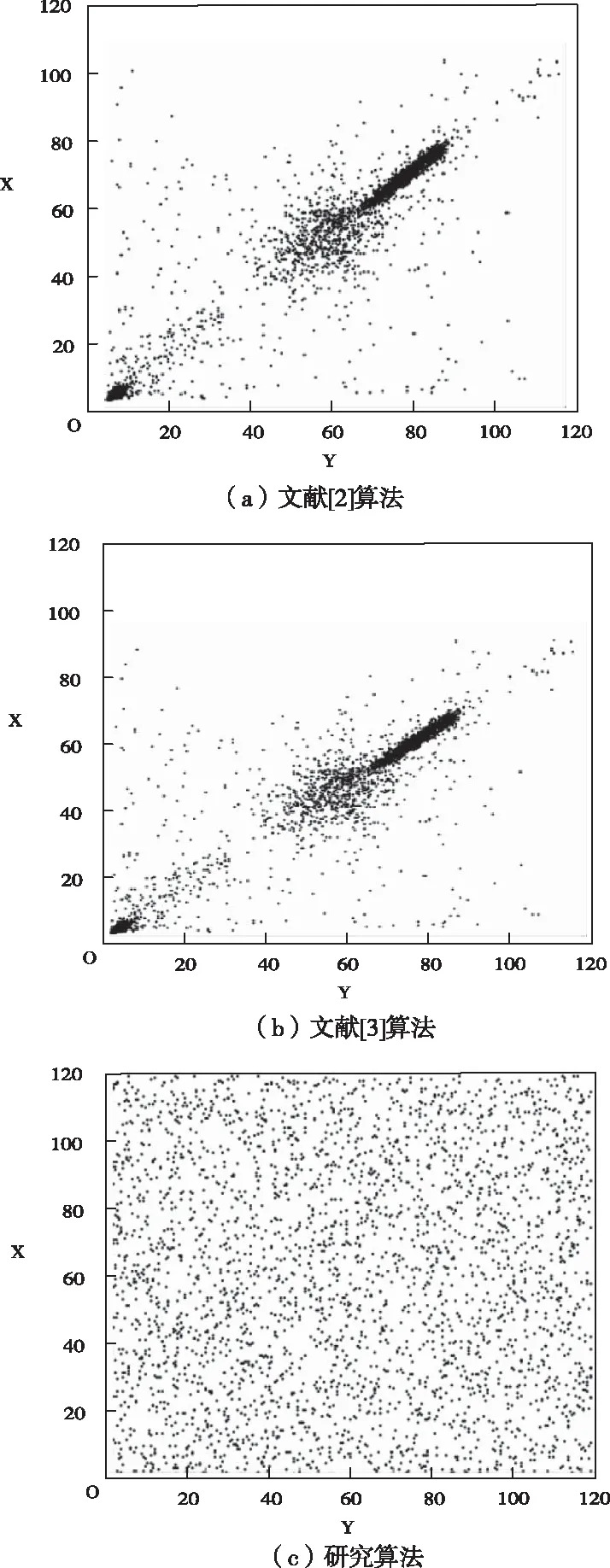
(11) 通过上式可知,该形式基的取模操作复杂度远比一般形式的小,从而令RSA密码算法的资源开销大幅度下降。 对大数Y进行分解后,m是二进制位宽[9],那么n是基二进制位宽,划分数量为p+1,那么得到 (12) 若大数Y被分解为P个部分,则表示形式如下所示 (13) 基于特殊形式的基,对式(2)进行改写,得到 (14) 如果εi与mi符合下列各条件式,则β为σk或者σk-1 (15) 按照位数从高到低的次序,采取相同转换方法,将Mi划分为p-1个部分,分解M为p个部分,且各部分均与硬件资源数据位宽相一致。 结合式(1),得出下列RSA密码算法的转换公式 xi=Xmodmi =(Xp2pn+Xp-12(p-1)n+…+X12n+X0)modmi (16) 为了验证本文提出的基于余数系统蒙哥马利模乘器的RSA密码算法的有效性,进行仿真。仿真环境的计算机配置是英特尔赛扬2.4G处理器,运行内存为512M,操作系统为Windows 10,程序编写软件为VC++6.0版本。 为了验证研究算法的可行性,对文献[2]算法、文献[3]算法以及研究算法分别进行仿真,所得的素数获取速率与RSA加密速率实验数据分别如下表所示。 表2 素数获取速率统计表(单位:s) 表3 RSA加密速率统计表(单位:ms) 通过上表中的各项数据可以看出,各算法的素数获取速度与RSA加密速度,均随着进制长度的增加而变慢。对于素数获取速率,相对于文献[2]算法,研究算法的速率分别提升了80%、44%、29.06%、36.48%,与文献[3]算法进行对比后,研究算法的素数获取速率则分别增加了41.67%、77.93%、56.54%、70.62%;对RSA的加密速率来说,相比文献[2]算法,研究算法的RSA加密速率分别上涨了19.01%、26.28%、20.01%、31.98%、27.52%、35.75%、30.68%、27.16%,而相对文献[3]算法,研究算法的加密速率上升幅度分别是9.93%、43.13%、13.76%、14.4%、12.88%、16.55%、15.91%、11.85%。通过以上两个结果验证了本文提出的基于余数系统蒙哥马利模乘器的RSA密码算法的有效性与可靠性。 在上述实验的基础上,对比三种算法的执行时间,结果如图2所示。 图2 三种算法执行时间比较 分析图2可知,文献[2]算法的执行时间在0-4.7s之间变化,文献[3]算法的执行时间在0-2.8s之间变化,而研究算法的执行时间始终低于1.0s,说明该算法的执行时间短、效率高。 比较三种算法的密码分布情况,结果如图3所示。 图3 密码分布情况比较 综合比较三种算法的密码分布情况可知,与其它两种算法相比,研究算法的密码分布更为均匀,说明该算法的加密性能更优。 随着信息技术的快速发展,信息安全问题日益突出,为了保证信息能够安全传输,因此RSA公钥加密算法被广泛应用于各个领域中。由于当前算法不符合大位宽的处理需求,执行时间长,所以本文设计了一种基于余数系统蒙哥马利模乘器的RSA密码算法。根据余数系统独特的无权属性,用一般二进制数值表示形式代替余数系统的表示形式。 利用双模式乘法器与硬件实现平台,设计余数系统蒙哥马利模乘器,采用余数系统通道组成各个模乘器,并微调至伪梅森素数,实现数据预计算。通过二进制位扫描模幂算法的预处理,将数表示形式转变为蒙哥马利域的表示形式,并按照幂指数有效位从高到低的顺序进行扫描,根据余数系统蒙哥马利模乘器中的数据依赖关系,构建RSA密码算法执行的预估时间公式,应用特殊基简化整个取模操作复杂度,采取相同转换形式实现RSA密码算法构建。实验结果表明,该算法素数获取速率与RSA加密速率高,执行时间短,加密效果更好。该算法为各领域的加密计算奠定了相关的运算基础,具有广阔的应用前景。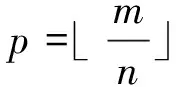
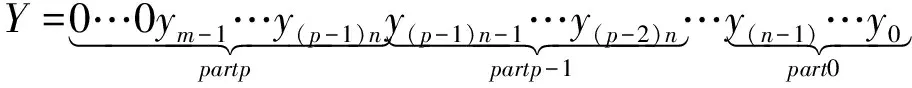
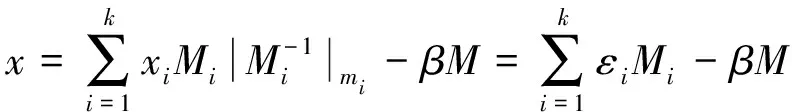
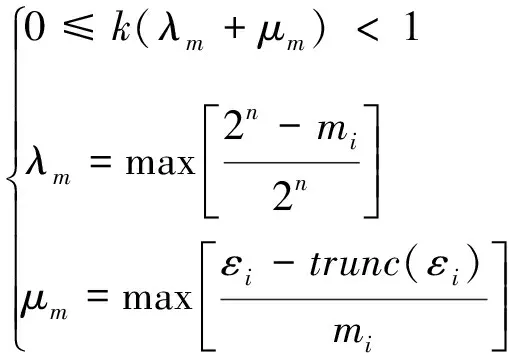
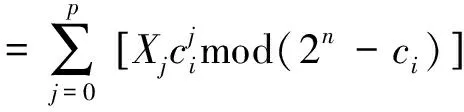
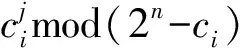
4 仿真研究
4.1 仿真环境
4.2 性能分析

5 结论
