基于灰色关联模型的遥测数据趋势异常分析

鄢青青 彭宗尧 柳振民

西昌卫星发射中心，西昌 615000

0 引 言

遥测数据反映了火箭飞行自身与内外环境的状态。趋势信息是进行火箭飞行故障诊断和排查的重要依据，可通过数据比对的方式来实现趋势一致性分析。目前，对数据趋势分析判读的方法主要有趋势预测[1]、统计假设检验方法[2]、残差分析法[3]、包络分析法[4]、相关系数法[5]、灰色关联分析[6]等。

灰色关联分析模型是根据序列曲线几何形状及空间距离来判断不同序列之间的联系是否紧密[7]。自1985年邓聚龙提出灰色关联度模型[8]以来，灰色关联分析已在多个领域得到应用和发展，如文献[9]基于形状相似性和距离接近性进行仿真一致性检验；文献[10]采用灰色关联模型评估空气质量趋势和空气污染治理效果；文献[7]和[11]分别基于相似性和接近性提出了4个关联度定义。

针对同参数不同历史过程数据的趋势一致性异常分析问题，通过计算分段关联度和分段异常度，增加关键局部异常的识别度，并提出基于异常均衡度和异常关联度的整体趋势异常评价方法，综合判断遥测数据的整体趋势与关键局部的异常情况。通过对历史数据进行分析，验证了该方法的可行性。

1 火箭遥测数据趋势异常问题

火箭遥测数据的趋势是判断火箭飞行状态的重要信息，其异常的时段、程度信息可用来定位、分析故障发生的原因、局部位置和影响范围等。

基于对比分析的遥测数据趋势异常分析方法，即趋势一致性分析，是以某参数在历史任务中的一次正常飞行数据作为参考序列，通过分析其当前数据(比较序列)与参考序列的趋势是否一致来进行故障状态识别或趋势预测。缓变遥测数据的趋势异常一般表现为与正常数据的局部持续的幅值偏差或从某时刻开始的长时间、跨时段幅值偏差，而偏差程度常表示所指示子系统的异常程度。

由于飞行弹道和火箭状态的差别，即使同样飞行正常的两个数据序列的趋势也并不完全一致，这种不一致主要体现在形状相似度、幅值距离和时长等方面。其中时长不一致易导致两个序列的相同特征部位发生平移和错位(如图1(a)所示)，增大一致性分析的难度；而因遥测数据的采样频率较高、火箭飞行时间较长，导致遥测数据的数据量极大，使局部幅值小偏差产生累积效应(如图1(b)所示)，影响后续时段形状相似性和距离接近性的分析准确性。

图1 同参数的数据序列不一致示例

火箭遥测数据可划分为不同的区间，对应箭上单机或子系统的不同工作或非工作时段，往往具有不同的变化特征和关注度，如在趋势分析中不加以区分，可能导致关键区间的相对较小异常被非关键区间的相对较大趋势异常掩盖。

2 灰色关联分析方法

(1)

表示X0和X1的灰色绝对关联度ε0i和灰色相对关联度r0i。

由于|s0|+|si|≥|s0-si|成立，故1+|s0|+|si|>|s0-si|也成立，如该不等式两侧同时加上左侧项，可得2×(1+|s0|+|si|)>1+|s0|+|si|+|s0-si|，即有下式表示的关系

(2)

由此可知，式(1)定义的灰色绝对关联度ε0i和相对关联度r0i的取值范围应为(0.5,1]，与邓氏灰色关联公理[8]中的规范性要求不符。

根据文献[11]对灰色相似关联度ψ0i和接近关联度ρ0i的定义，该关联度模型在数据量较小时能较好地反应两个序列的关联程度。当数据量较大时，除非两个序列极其相似且空间距离极小，否则即使存在很小的偏差，在大量数据的积累效应下，仍会导致|s0-si|远大于|x0(k)-xi(k)|的量纲级别，从而使关联度计算值在一个极小的值域内变化，并且关联度在区间(0,1]内呈严重不均匀分布。如图2所示，从某一温度遥测数据序列中选取时长为4000个时间单位的数据分段作为基准(如图2(a))，并从该数据序列中随机选取相同时长的分段与基准分段按文献[11]计算相似和接近关联度，共得约67000个结果，排序后绘制图2(b)。可见绝大部分关联度计算值均接近0，对分段间关联关系的反映不够准确。

图2 大数据量时的关联度分布示意

对数据量或序列长度较大的两个序列，大量小偏差的积累也易产生较低的整体关联度，从而掩盖局部趋势异常。如图3所示，序列X3有局部趋势异常，X1无局部趋势异常，分别计算X2与X1，X3的整体关联度(见表1)，可见X2与X3之间的整体关联度稍大于X2与X1的整体关联度，如果仅依据整体关联度，则无法发现X3的趋势异常问题。

图3 某参数的3个历史数据序列

表1 X2与X1，X3的整体关联度计算结果

综上所述，在应用文献[11]中灰色关联模型进行遥测数据趋势一致性分析中，数据量大、局部特征时轴偏移及幅值偏差累积等特点会掩盖局部异常、降低关联分析的准确性。

3 改进的趋势一致性异常分析方法

3.1 文献[11]中关联度模型的适应性改进

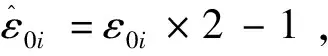
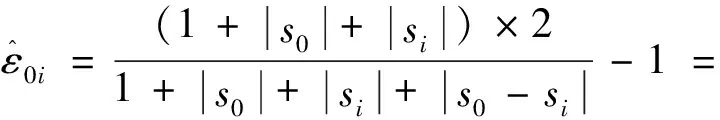
(3)

对文献[11]中灰色相似关联度ψ0i和接近关联度ρ0i模型做如下修改

(4)

(5)

图4 改进的相似关联度和接近关联度值域测试

3.2 遥测数据趋势一致性异常分析

3.2.1 分段异常度计算

遥测数据根据其关联控制参数的指令发出时间，可划分为具有不同的变化特征的区间[12]。

ym=ωm(1-Γm)

(6)

3.2.2 遥测数据整体趋势异常评价

通过异常均衡度和异常关联度2个指标来分析评价两个序列的整体趋势一致性异常情况。

(1)异常均衡度

为评价各分段异常度是否均衡，采取文献[13]改进的均衡度定义方法定义异常均衡度为

(7)

1)b(σ(y1,y2,…,yM))=b(y1,y2,…,yM)，σ(y1,y2,…,yM)是{y1,y2,…,yM}的一个置换；

2)Y≠0时，b(y1,y2,…,yM)=1；

3)b(y1,y2,…,yM)关于ym连续，∀m∈{1,2,…,M}；

(2)异常关联度

为评价比较序列X1的整体异常程度，采取类似接近关联度的方式，定义异常关联度为

(8)

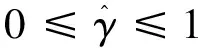
联合异常均衡度与异常关联度2个指标，可以分析两个序列的整体趋势一致性及其异常情况。2个指标的判读阈值可根据实际应用中的经验值、判读严格程度确定。

4 应用分析

4.1 分段关联度

取某参数的2个历史遥测数据序列X1和X2，序列X2时长较X1短约20s，且两个序列被4个关联控制参数时刻划分为5个对应分段。以序列X2为参考序列，则从图5中可见比较序列X1相对X2存在局部趋势异常。对5个分段分别进行插值对齐后组成新的序列X′1和X′2。

图5 遥测数据序列X1和X2分段插值后

对序列X′1和X′2分别计算各对应分段关联度、平均关联度(分段关联度的平均值)、整体关联度(X′1与X′2的关联度)见表2。分析可知，序列X′1和X′2的5个对应分段中，分段1和分段5的形状相似性较差，但分段1的距离接近性和相对始点变化速率相似性优于分段5，分段2～4的4类关联性均相对较好。

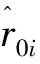
表2 遥测数据序列X′1与X′2的关联度

4.2 局部异常度

采用1～9标度法[14]获取序列X′1和X′2的5个对应分段的权重向量为ω′=(0.143,0.333,0.048,0.333,0.143)，ω″=(0.100,0.233,0.333,0.233,0.100)以及ω‴=(0.107,0.250,0.036,0.250,0.357)，计算各对应分段的异常度和平均异常度，计算结果见表3。

表3 遥测数据序列X′1与X′2的异常度

ω″相对ω′，分段3的权重明显增大，而其他几个分段权重不同程度减小，反映到表3可见，仅分段3的异常度增大，其他几个分段的异常度均减小。ω‴相对ω″，分段5的权重明显增大，而分段3的权重明显减小，且分段5的权重增大程度小于分段3的权重减小程度，但反映到各分段的异常度中，分段5的异常度增大程度却大于分段3的异常度减小程度。ω‴相对ω′，分段5的权重明显增大，其他几个分段权重不同程度减小，反映到各分段的异常度中，分段5的异常度明显增大，而其他几个分段的异常度均减小，而分段1的异常度减小程度也相对大于其他几个分段。

因此可知，权重可直接影响各分段的异常程度，特别是对存在趋势异常的分段1、5的影响更加明显(即使在权重接近的情况下比较，如ω″中分段3权重为0.333，ω‴中分段5权重为0.357，而ω‴作用下的分段5异常度明显大于ω″作用下的分段3异常度)。而平均异常度虽然也随异常分段的权重增大而有所增大，但幅度不明显，无法用于判断整体的异常情况。

4.3 整体趋势一致性异常评价

对遥测数据对齐序列X′1和X′2，分别以上述3个权重向量ω′，ω″和ω‴所计算的5个分段的4类异常度为异常度序列Y，根据式(7)计算3个权重向量下的4类异常均衡度如表4。

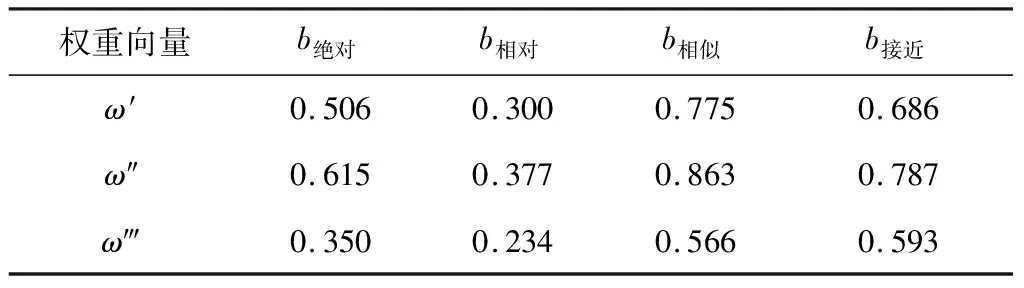
表4 3个权重向量下的4类异常均衡度

根据式(8)计算两个序列的异常关联度，同时，通过式(9)计算两个序列的分段综合关联度，对比如表5。

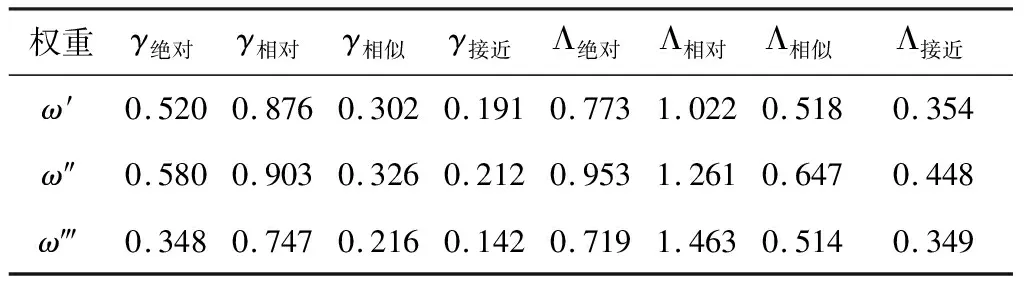
表5 异常关联度及其与综合关联度的对比

(9)

在上述两表中，比较3个权重向量作用下的整体趋势一致性，ω‴作用下γ绝对、γ相似、γ接近均较小，但b相似和b接近为中偏大，表明两个数据序列X′1和X′2在ω‴作用下相似性和接近性存在局部异常，从ω‴的取值可知，存在趋势异常的分段5的权重最大，而分段2、4也被相对较大的权重放大了异常程度，从而导致b相似和b接近为中偏大。ω′和ω″作用下γ绝对，γ相似和γ接近也偏小，但对应的异常均衡度b，b相似和b接近偏大，特别是ω″作用下的异常均衡度最大，说明ω″将原本的趋势异常分段的异常程度缩小，而放大了原本异常不明显的分段的异常程度，使趋势异常的局部增多而整体的异常程度稍有下降，这从ω″的取值可以看出，分段1、5的权重在3个权重向量中最小，而其他3个分段的权重增大。在3个权重向量作用下，γ相对均偏大，而b相对较小，说明两个序列相对始点变化率的相似度为中偏大，且存在少量局部异常，但局部异常程度偏小。

ω′相对ω‴减小了分段1、5的权重，增大了分段2、4的权重，使ω′作用下的异常均衡度和关联度相对ω‴作用下均有增大；ω″相对ω′进一步减小分段1、5的权重，增大分段3的权重，使异常均衡度和关联度进一步增大。

由此可知，异常均衡度和异常关联度准确反映了两个序列的整体趋势一致性，及其随权重向量的变化过程，有助于判断序列的整体趋势及局部异常情况。

将表5中的异常关联度与综合关联度、表2中的整体关联度对比发现，综合关联度不但无法直观反映整体趋势一致性，而且对权重变化的响应也不够灵敏(ω′相对ω‴作用下变化不明显)；而整体关联度对整体趋势一致性反映不够准确，更无法用于判断是否存在局部异常，也无法体现分段权重对整体趋势的影响。

5 结论

根据火箭遥测数据的特点，提出一种基于改进关联度模型的趋势异常分析方法。在对文献[11]中关联度模型进行适应性改进的基础上，通过计算分段关联度，降低局部幅值偏差累积和特征时轴偏移对整体关联度的影响；而引入权重的分段异常度则进一步增加关键局部异常的识别度。提出基于异常均衡度和异常关联度的整体趋势异常评价方法，以从整体上综合判断遥测数据的趋势一致性与关键(重要)局部的异常情况。通过对历史遥测数据序列进行分析，验证了基于改进灰色关联模型的遥测数据趋势异常分析模型的可行性。