半主动升沉补偿系统的非线性建模与仿真

展 勇， 吴少飞， 付钧升， 徐建安， 丁毅然

(哈尔滨工程大学 机电工程学院， 黑龙江 哈尔滨 150001)

引言

我国的海洋资源开发和海洋工程技术正处于快速发展阶段，对安全可靠的海工设备的需求日益增加。船舶在海上进行起重和打捞作业时，受风浪的影响，会产生剧烈的升沉运动，这会给海上作业带来很大的难度和安全隐患。为了提高起重机的定位精度和平稳性，需要将升沉补偿技术应用于起重设备上。目前，大负载升沉补偿技术主要被西方国家垄断， 但是国内的升沉补偿理论研究也取得了许多突破性进展。胡中望等[1-2]提出了一种船舶起重机半主动升沉补偿系统补偿控制方法，深入分析了重载半主动波浪补偿的功率特性，研究了海浪幅值、海浪周期和负载质量等参数变化对补偿精度和系统能耗的影响规律。姜浩等[3]设计了一种浮式钻井平台半主动波浪补偿系统，具有较高的补偿精度，实现了稳定钻压和提高钻速的目的。周利等[4]针对主动补偿系统的时滞性，设计了一种模糊预测控制算法，在提高系统稳定性的同时，保证了系统的抗干扰性。范珂等[5]设计了一种自适应鲁棒控制器，可以有效改善主动升沉补偿系统的非线性问题。

目前，国内外升沉补偿系统的研究主要集中在对机械结构和控制算法的改进上[6-8]，鲜有在建模时考虑液压缸所受的非线性力。实际上，液压缸在使用过程中，非线性力会使得系统响应变慢，误差增加。对液压缸进行非线性建模，可以提高升沉补偿系统建模的精确度，从而获得更加贴近现实的仿真结果。本研究着重对液压缸所受非线性摩擦力和非线性弹簧力进行建模，在此基础上提出了一种半主动升沉补偿系统的非线性建模方法，并提出了一种可以提高升沉补偿效率的方案。

1 液压缸所受非线性力的建模与仿真

1.1 液压缸的动力学模型

液压缸在工作过程中，除了会受到来自负载的推力和来自液压油的压力之外，还会受到非线性摩擦力和非线性弹簧力的影响，液压缸的动力学模型如图1所示。

图1 液压缸动力学模型

液压缸的动力学方程为：

(1)

式中，m—— 负载和活塞等效总质量

Fs—— 非线性弹簧力

Ff—— 非线性摩擦力

p1—— 进油腔压力

A1—— 进油腔横截面积

p2—— 回油腔压力

A2—— 回油腔横截面积

FL—— 负载力

1.2 非线性摩擦力的数学模型

液压缸在工作过程中受到的摩擦力是非线性的，摩擦因数的大小与润换状态的关系满足Streibeck效应[9]，非线性摩擦力与活塞相对运动速度v的关系如图2所示。

图2 摩擦力与活塞相对运动速度的关系曲线

本研究使用LuGre模型对液压缸的非线性摩擦力进行建模，该模型能较精确的描述摩擦的稳态、瞬态特性，如黏滑运动、预位移、静摩擦、库仑摩擦、Stirbeck 效应和摩擦滞后[10]，其数学模型可表示为：

(2)

式中，z—— 微观鬃毛的平均挠度

σ0—— 微观鬃毛的刚度

σ1—— 微观鬃毛的阻尼系数

σ2—— 系统的黏性摩擦因数

vs—— Stribeck临界速度

g(v) —— Stribeck 摩擦曲线函数

fc—— 库仑摩擦力

fs—— 静摩擦力

1.3 非线性弹簧力的数学模型

液压缸的弹簧刚度可以看作由液压油刚度和活塞杆刚度串联而成。液压油的弹性模量一般在1.4～2.0 GPa之间，而制作活塞杆的钢的弹性模量是液压油的100～150倍，所以可以忽略活塞杆的弹性变形，因此系统的非线性弹簧力主要来自于液压缸、进出油管路和蓄能器内的液压油所构成的液体弹簧[11]。

液体封闭容腔压力基本公式为：

(3)

式中， Δp—— 封闭容腔的压力变化值

Kv—— 液压油的体积弹性模量

ΔV—— 压力增大Δp时，封闭容腔体积的减小量

V—— 封闭容腔的初始体积

液压缸在工作时，活塞杆的移动会引起液体弹簧刚度的变化，其规律可以表示为：

k(x)=KvA1[1/(L1+x)+(A2/A1)/(L-L1-x)]

(4)

式中，L1—— 进油腔液柱初始长度

L—— 液压缸总行程

x—— 工作点位置

令y为活塞在工作点x附近的振动位移，即y=Δx。将式(3)在工作点处展开，可以得到：

(5)

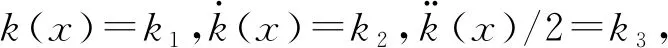
Fs=k(x+y)y=k1y+k2y2+k3y3

(6)

由于液压缸的弹性势能U具有对称性：

U=k1y2/2+k3y4/4

(7)

故液压弹簧力可以简化为：

(8)

1.4 两种非线性力的仿真结果

以被动补偿缸为仿真对象，根据式(2)，使用Simulink建立非线性摩擦力的仿真模型，由于LuGre模型中的一些参数难以通过实验测试，因此基于经验进行计算和估计相关参数[12-13]，如表1所示。

表1 非线性摩擦力仿真模型所需参数

用斜率为0.5的斜坡函数作为速度输入，得到的仿真结果如图3所示。

图3 非线性摩擦力模型仿真结果

以被动补偿缸为仿真对象，根据式(8)，使用Simulink建立非线性弹簧力的仿真模型，仿真需要的参数如表2所示。

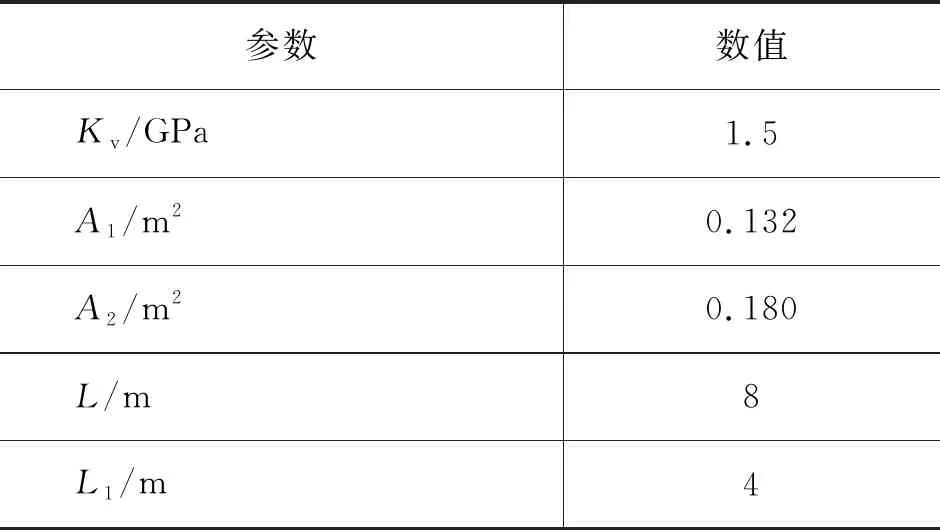
表2 非线性弹簧力仿真模型所需参数

用幅值为0.1 m、周期为10 s的正弦信号作为振动位移输入，得到的仿真结果如图4所示。

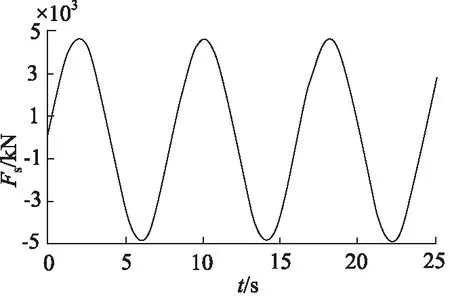
图4 非线性弹簧力模型仿真结果

2 被动升沉补偿仿真模型的建立

已知五级海况的波高为5～8 m，周期为3.8～13.6 s，本研究选用峰值为6 m、周期为10 s的正弦信号作为船舶的升沉位移信号。

为了研究液压缸非线性力对升沉补偿系统的影响，需要建立被动升沉补偿仿真模型，其原理如图5所示。

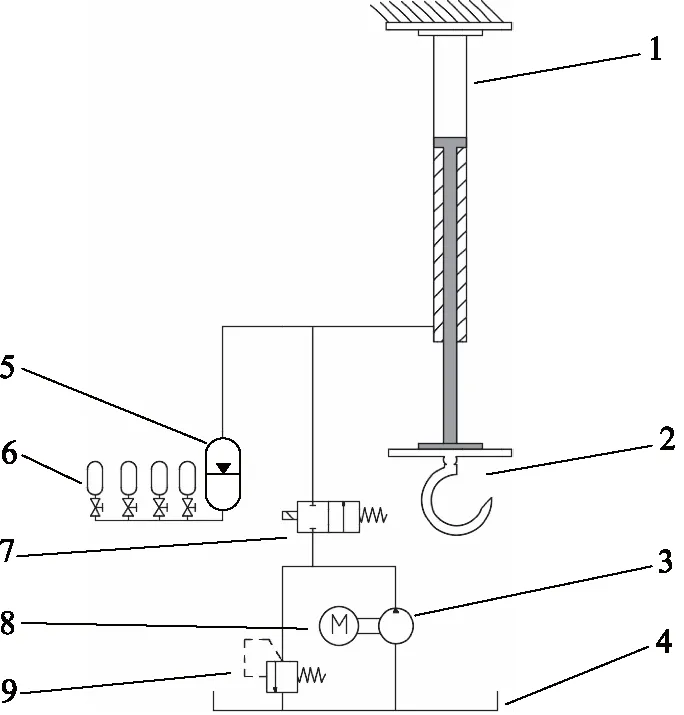
1.被动补偿缸 2.大钩 3.定量泵 4.油箱 5.蓄能器 6.气瓶组 7.开关阀 8.马达 9.溢流阀

本系统采用悬挂式布置，被动补偿缸1固定在船舶起重机上，活塞杆与大钩2采用法兰连接，大钩2与载荷连接，其余液压装置可布置于甲板上。开关阀7连通时，定量泵3可向蓄能器5和被动补偿缸1的有杆腔内供油；补偿系统工作时，开关阀7断开；吊放货物时，蓄能器5、气瓶组6和被动补偿缸1中的气体和液压油组成的气-液弹簧不断吸收和释放能量，进而达到升沉补偿的目的[14]。

使用AMESim和Simulink联合仿真，在AMESim中设置好液压油的体积弹性模量、液压缸长度、液压缸及活塞杆的直径等数值，AMESim在仿真过程中就会体现出非线性弹簧力对被动升沉补偿系统的影响，被动升沉补偿仿真模型如图6所示。

1.负载和活塞等效模型 2.速度传感器 3.蓄能器 4.管路 5.被动补偿缸 6.联合仿真模块 7.信号输入模块

图6中模块6将采集到的活塞相对于液压缸的速度信号，输入到Simulink中，经过计算得到非线性摩擦力的值，再将摩擦力的值返回到AMESim仿真模型中，作用于被动补偿缸上，建立模型所需的参数设置，如表3所示。

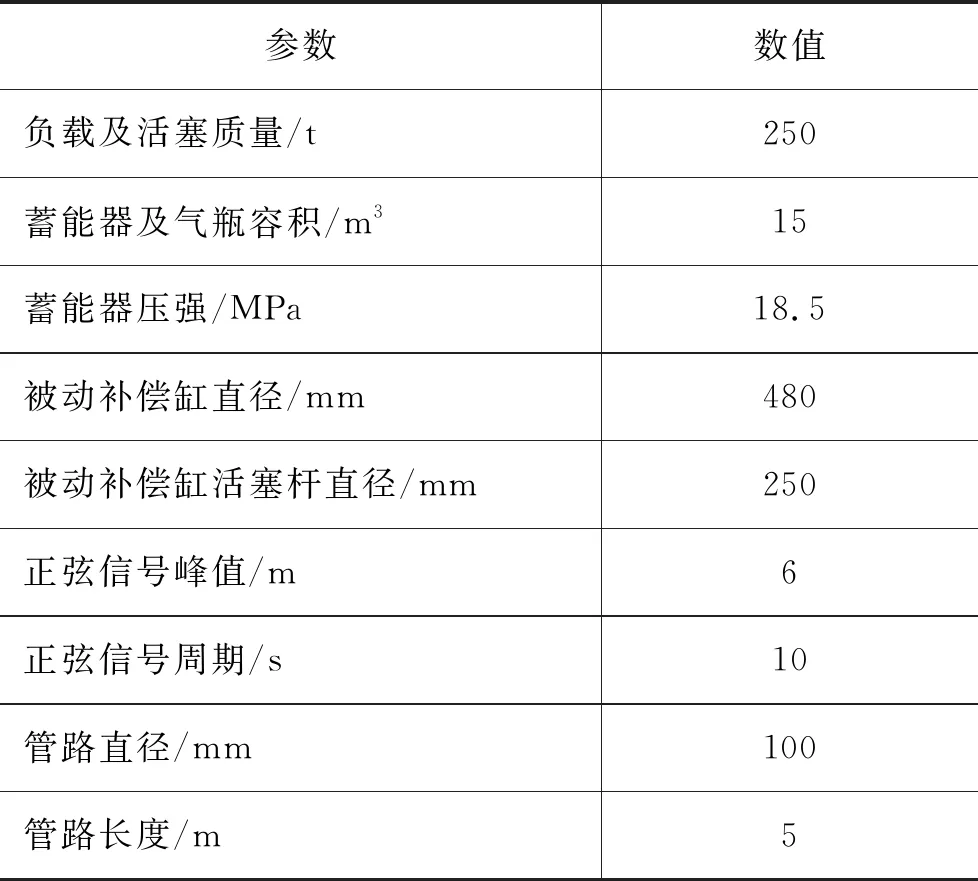
表3 被动升沉补偿模型所需参数

3 半主动升沉补偿仿真模型的建立

本研究设计的半主动升沉补偿系统是将1个被动补偿缸和1个主动补偿缸进行并联，共同对负载的升沉运动进行补偿，其原理如图7所示。

1.主动补偿缸 2.大钩 3.电磁换向阀 4.定量泵 5.油箱 6.被动补偿缸 7.蓄能器 8.气瓶组 9.开关阀 10.马达 11.溢流阀

本系统在图5所示的被动升沉补偿系统的基础上添加了主动升沉补偿部分。控制器通过采集载荷的升沉位移信号，经过处理后将其转化为活塞相对于液压缸体的期望位移，并利用此信号来控制电磁换向阀的开口方向及大小，控制主动补偿油缸的活塞位置，实现半主动升沉补偿[15-16]。

使用AMESim和Simulink联合仿真，建立半主动升沉补偿仿真模型如图8所示。

1.主动补偿缸 2.位移传感器 3.PID控制器 4.电磁换向阀 5.能耗计算模块 6.定量泵 7.马达 8.联合仿真模块

该模型中，摩擦力计算方法与被动升沉补偿相同，将计算得到的摩擦力分别加在主动补偿缸和被动补偿缸上。负载、输入信号和被动补偿部分的参数与表3中的一致，建立模型所需的其余参数设置如表4所示。

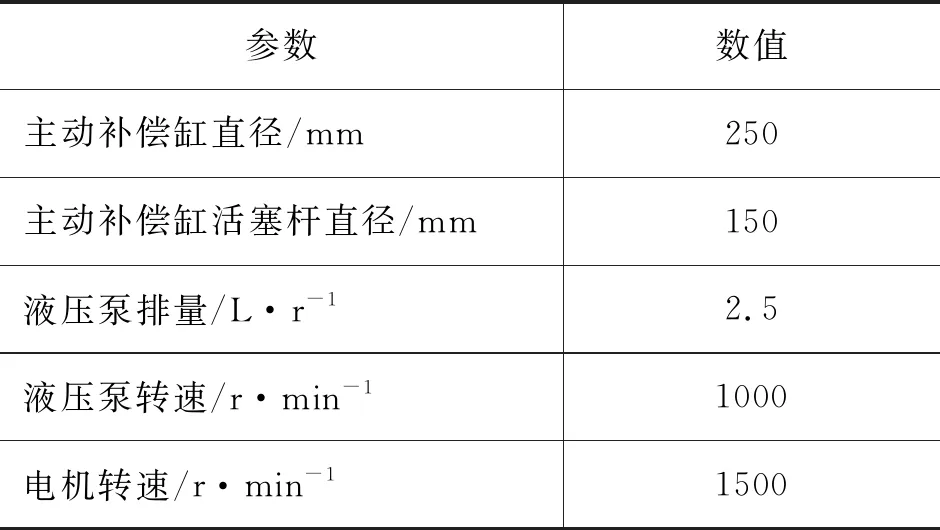
表4 半主动升沉补偿模型所需参数

4 仿真结果及分析

4.1 非线性摩擦力的影响

本节中将液压油体积弹性模量设置为1.7 GPa，非线性摩擦力的参数设置与表1相同。

分别在考虑非线性摩擦力和不考虑非线性摩擦力的情况下，对被动升沉补偿系统进行仿真，仿真结果如图9所示。

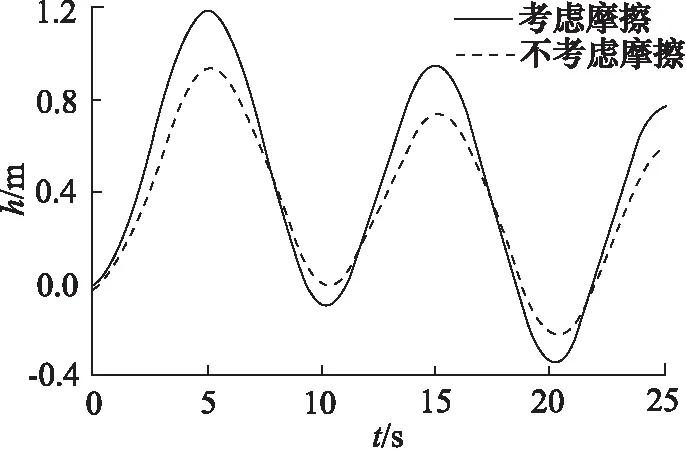
图9 非线性摩擦力对被动升沉补偿系统的影响

由图9可知，在船舶升沉位移峰值为6 m时，不考虑摩擦力影响的情况下，被动升沉补偿的负载位移h在0.95 m左右，补偿效率为84.2%；考虑摩擦力影响的情况下，被动升沉补偿的负载位移在1.2 m左右，补偿效率为80.0%。可以看出，在加入了非线性摩擦力之后，被动升沉补偿系统的补偿效果变差。

分别在考虑非线性摩擦力和不考虑非线性摩擦力的情况下，对半主动升沉补偿系统进行仿真，仿真结果如图10所示。

图10 非线性摩擦力对半主动升沉补偿系统的影响

由图10可知，在船舶升沉位移峰值为6 m时，不考虑摩擦力影响的情况下，半主动升沉补偿的负载位移在0.2 m左右，补偿效率为96.7%；考虑摩擦力影响的情况下，半主动升沉补偿的负载位移在0.55 m左右，补偿效率为90.8%。可以看出，在加入了非线性摩擦力之后，半主动升沉补偿系统的补偿效果变差。

4.2 非线性弹簧力的影响

根据式(3)可知，补偿系统内液压油的弹性形变与容腔内压力变化有关，被动升沉补偿系统和半主动升沉补偿系统的蓄能器压力变化如图11和图12所示。

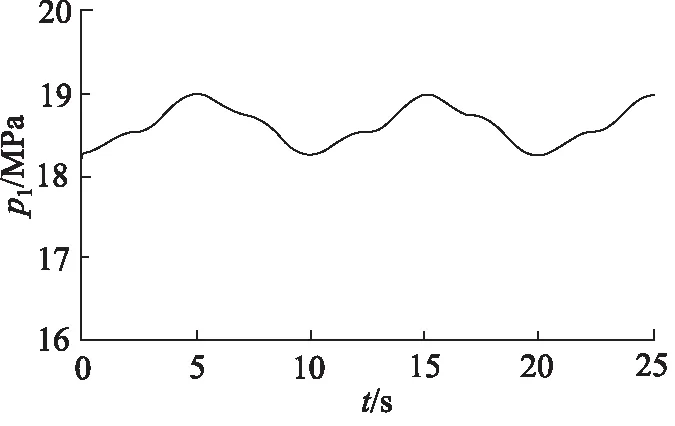
图11 被动升沉补偿系统蓄能器压力p1变化

图12 半主动升沉补偿系统蓄能器压力p2变化

已知被动补偿缸的有杆腔横截面积为0.132 m2，行程为7 m，被动补偿缸和蓄能器之间的油管孔径为100 mm，长度为5 m，蓄能器体积为2 m3。经过计算，在平衡位置时，被动补偿缸、管路和蓄能器内的液压油体积V1约为1.5 m3。由图11和图12可知，被动升沉补偿系统的蓄能器压力变化值Δp1约为0.8 MPa，半主动升沉补偿系统的蓄能器压力变化值Δp2约为1.2 MPa。取液压油体积弹性模量为1.5 GPa，将上述参数代入式(3)可得，被动升沉补偿系统内油液弹性变形量为：

(9)

同理可得，半主动升沉补偿系统的被动缸-蓄能器容腔内油液弹性变形量为：

(10)

在本研究设计的被动升沉补偿系统和半主动升沉补偿系统中，油液的弹性变形量相对较小。

在液压油的体积弹性模量为1.5 GPa和2.0 GPa，其他参数均相同的情况下，分别对被动升沉补偿系统和半主动升沉补偿系统进行仿真，结果如图13和图14所示。

由图13和图14可知，改变液压油的体积弹性模量对仿真结果的影响很小，综合式(9)和式(10)的计算结果， 可以认为液压油的弹性变形产生的非线性弹簧力对升沉补偿系统的影响很小，因此在仿真中可忽略不计。

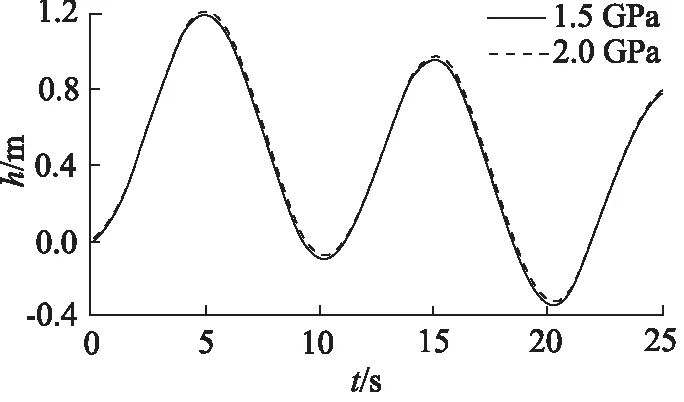
图13 非线性弹簧力对被动升沉补偿系统的影响

图14 非线性弹簧力对半主动升沉补偿系统的影响

4.3 提高半主动升沉补偿系统效率的方法

图8所示的半主动升沉补偿系统中，连接蓄能器和被动补偿缸的管路长度为5 m，直径为100 mm，长径比大于4，属于细长小孔，其流量公式可以表示为：

(11)

式中，d0—— 蓄能器和被动补偿缸之间的管路直径

Δp0—— 蓄能器和被动补偿缸之间的管路两端压力差

μ—— 油液的黏性阻尼系数

l0—— 蓄能器和被动补偿缸之间的管路长度

被动补偿缸单位时间内的活塞位移可以表示为：

(12)

式中，Ab为被动补偿缸有杆腔横截面积

由式(11)和式(12)可知，在其他条件不变的情况下，增大d0，可使该管路流量增大，单位时间内进出被动补偿缸的液压油体积增多，活塞运动的幅度增大，该公式同样适用于主动升沉补偿部分的管路。因此增大半主动升沉补偿系统的管路直径，可以提高升沉补偿效率。

为了验证该结论，分别在d0为100 mm和150 mm，其他参数均相同的情况下，对半主动升沉补偿系统进行仿真，结果如图15所示。

图15 管路直径对半主动升沉补偿系统的影响

由图15可知，增大蓄能器和被动补偿缸之间的管路直径，可以有效提高补偿效率。

5 结论

本研究建立了液压缸非线性摩擦力和非线性弹簧力的模型，在此基础上建立了被动升沉补偿系统和半主动升沉补偿系统的非线性仿真模型，由AMESim-MATLAB联合仿真结果可知：

(1) 液压缸非线性摩擦力对半主动升沉补偿系统的影响较大，使其补偿效率明显降低，而非线性弹簧力对升沉补偿系统的影响较小；

(2) 在其他条件不变的情况下，可以通过增大蓄能器和被动补偿缸之间的管路直径来提高半主动升沉补偿系统的补偿效率。

本研究限于实验条件，仅根据经验估计了非线性摩擦力LuGre模型中的一些参数，因此对得出的仿真结果仅能做出定性分析。下一步计划建立半主动升沉补偿系统的缩比样机，测量出液压缸的摩擦力-速度曲线，使用LuGre模型对测得的摩擦力进行拟合，验证本研究所建立的模型的正确性。