基于升力面自由尾迹的深海浮式风力机全耦合模型仿真研究
2021-11-17尹凡夫黄亚振
高 伟, 尹凡夫, 沈 昕, 黄亚振
(1.中国大唐集团科学技术研究院有限公司,北京 100040;2.中国大唐集团新能源科学技术研究院有限公司,北京 100052;3.上海交通大学 机械与动力工程学院,上海 200240)
近年来,随着陆上风电市场逐渐饱和,浮式风力机呈现出大型化、深海化的发展趋势。浮式风力机受力复杂,其气动、水动以及系泊之间存在更复杂的耦合关系,在考虑系统稳定性的同时又要兼顾浮式风力机的功率特性和经济性。基于固定式风力机或传统海洋工程结构体的计算方法无法完全满足浮式风力机的仿真需求。
浮式风力机气动预测方法主要包括动量叶素法(BEM)、基于N-S方程的计算流体力学(CFD)方法以及涡流理论[1-2]。目前,大多数浮式风力机工程计算软件的气动模块均基于BEM及其经验修正模型[3],但BEM存在很难捕捉流场细节的问题,且在高度非定常工况下其动量平衡假设不再成立[4]。CFD方法的计算精度很高, Tran等[5-6]运用重叠网格技术完成了浮式风力机在多种运动形式下的非定常气动分析。Liu等[7]将CFD方法推广到水动力求解中,开发了FOAM-SJTU求解器,完成了浮式风力机的全耦合模型代码。然而,CFD方法不能满足浮式风力机大量工况的计算要求。涡流理论的计算精度和效率均处于BEM与CFD方法之间,有望逐步替代BEM成为浮式风力机气动预测的主流方法。Jeon等[8]运用涡格法研究了NREL 5 MW某型浮式风力机在纵摇运动下的非定常气动特性。Wen等[9]利用自由尾迹模型评估了在纵摇运动下浮式风力机整个工作区域的功率性能。Shen等[10-11]开发了基于升力面自由尾迹模型的气动预测方法,完成了浮式风力机纵荡和纵摇运动的非定常气动特性分析。
综上,升力面自由尾迹的气动预测方法兼顾了计算精度和速度,但关于基于该方法的浮式风力机全耦合模型的研究还不够充分。笔者基于升力面自由尾迹方法建立浮式风力机的全耦合模型,考虑浮式风力机系统所受的气动力、水动力及系泊力,并采用多体系统动力学模型研究其运动响应。
1 研究方法
以Spar式深海浮式风力机为例,建立全耦合模型,见图1。
1.1 多体系统动力学模型
典型的浮式风力机系统可以简化为浮式平台、机舱、塔架和风轮(包括叶片和轮毂)4个刚性实体,浮式平台与塔架通过固定铰联结,无相对运动;塔架与机舱以固定铰联结;机舱与风轮通过旋转铰联结,暂不考虑变桨运动。建立的浮式风力机坐标系见图2。
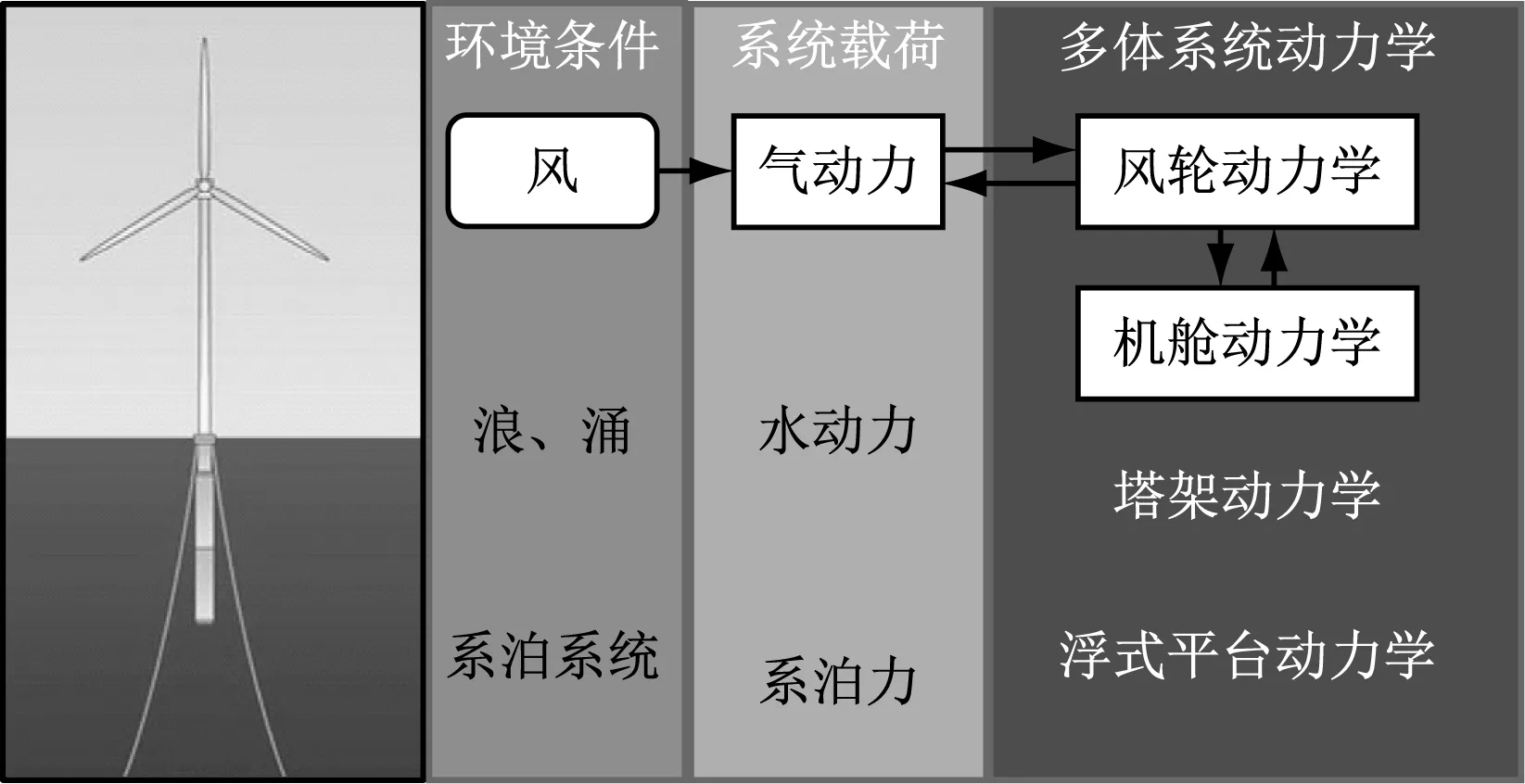
图1 浮式风力机全耦合模型Fig.1 Full coupling model of the floating wind turbine

图2 浮式风力机坐标系Fig.2 Coordinate system of the floating wind turbine
浮式风力机系统共存在24个自由度,其中独立自由度有7个。假定在浮式风力机稳定运行过程中风轮转速φ′恒定且已知,因此浮式风力机系统未知且独立的自由度仅6个。
基于拉格朗日第二类方程[12]建立了浮式风力机的多体系统动力学方程。
(1)
式中:t为时间;T为浮式风力机系统总动能;Q为系统广义坐标矩阵;Q′为Q的一阶导数;FQ为主动力矩阵F所对应的广义力矩阵。
一般取某广义坐标的变分δωj,令其他广义坐标的变分为0,计算由于该变分引起的各主动力所作的虚功δWj,即
FQ(j)=δWj(F,δωj)/δωj
(2)
主动力F包括各部件的重力G、风轮所受的气动力Fair、浮式平台所受水动力Fhydro及系泊系统带来的系泊力Fmooring。
F=Fair+Fhydro+Fmooring+G
(3)
1.2 升力面自由尾迹模型
升力面自由尾迹模型是一种基于涡流理论的适用于大展弦比薄翼的流场近似计算方法,相比于BEM和CFD方法,该方法兼顾了计算精度和计算效率。
基于势流理论的升力面法是在叶片参考面沿展向和弦向布置涡片或涡线,以代替真实叶片;相比于升力线法,升力面法考虑了叶片弦向的涡量变化,更接近真实叶片的气动状态。而涡格法是升力面法中最常见的数值求解方法,其示意图见图3。在每个控制点上均满足物面边界条件。
Vctrl·nctrl=0
(4)
式中:nctrl为控制点的物面法向量;Vctrl为控制点处的有效入流速度。
Vctrl=U∞+Vrlv+Vind
(5)
式中:U∞为入流速度;Vrlv为相对旋转速度;Vind为诱导速度。
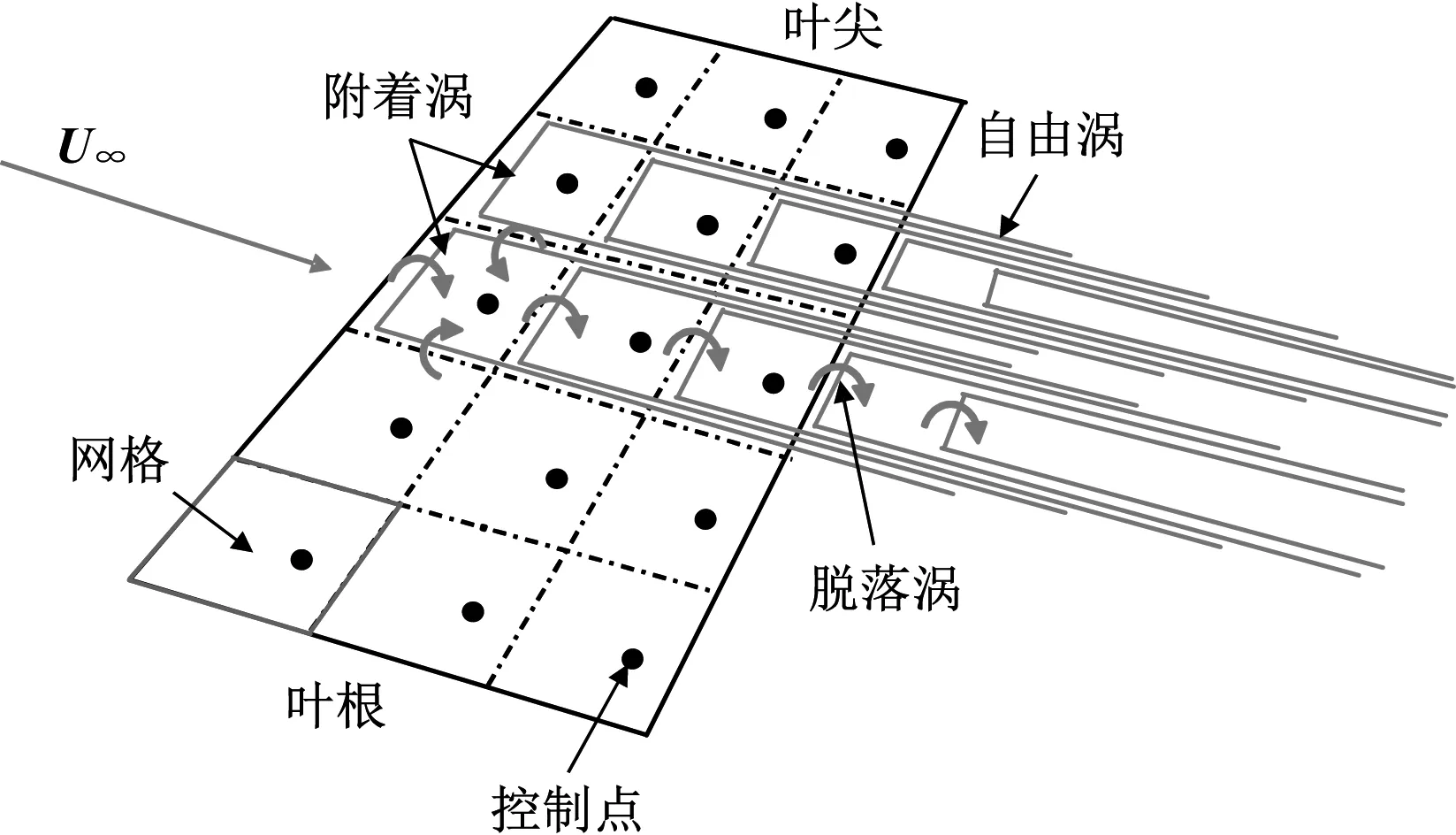
图3 涡格法示意图Fig.3 Schematic diagram of vortex lattice method
基于毕奥-萨伐尔(Biot-Savart)定理,已知环量的大小及空间分布,可得到控制点处的诱导速度。
理论上,叶片尾缘脱出的自由涡会延伸到下游无限远处,求解其环量分布和几何外形会耗费计算资源。实际上,叶片尾缘的自由涡随时间延长会向叶根和叶尖方向卷起,进而形成叶根涡和叶尖涡,其中叶根涡会很快消散,但叶尖涡会向下游不断延伸,对下游流场影响较大。因此,将叶片尾缘的自由涡简化为近场的涡面和远场的叶尖涡线,如图4所示。
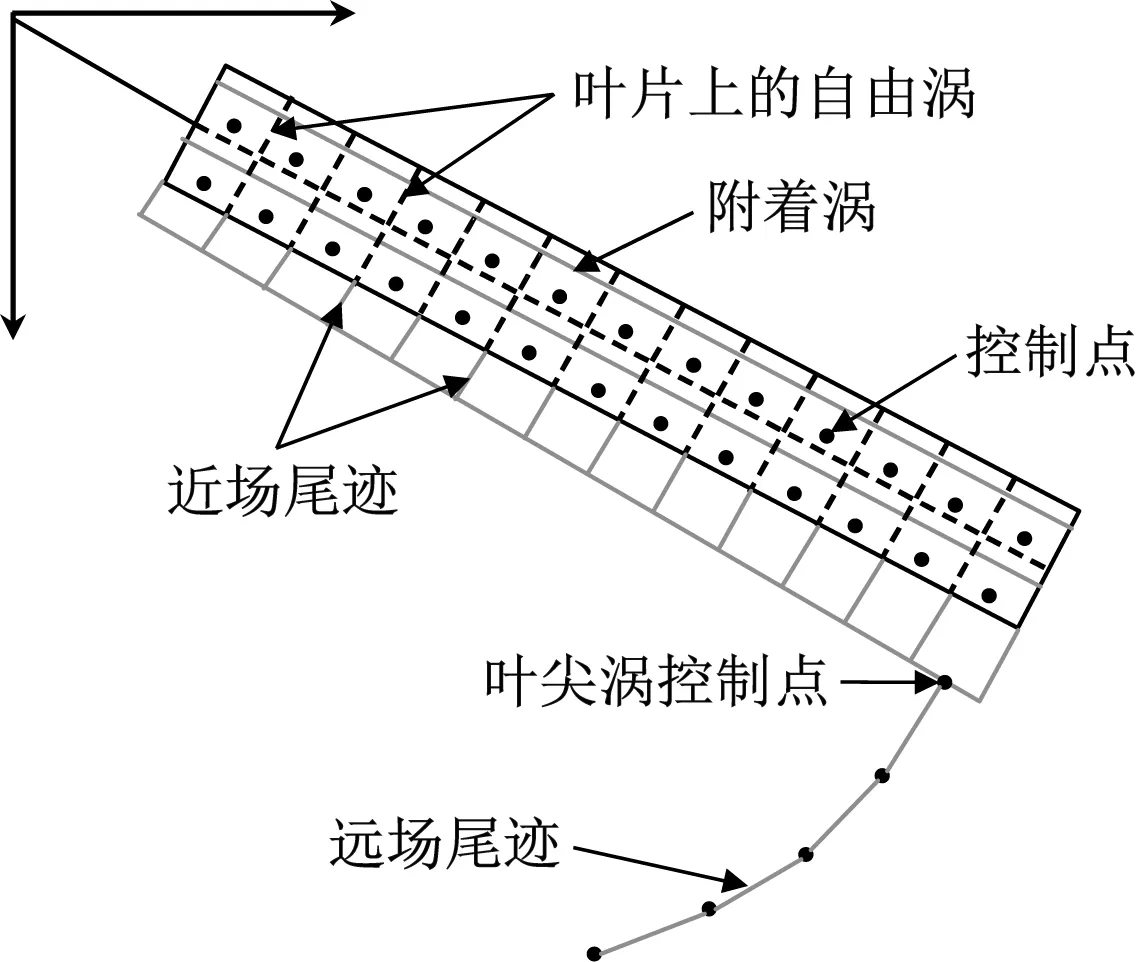
图4 叶片尾缘自由涡结构示意图Fig.4 Schematic diagram of free vortex structure at bladetrailing edge
浮式风力机运行时叶尖涡控制点的运动方程为:
(6)
式中:Ω为风力机转速;r为控制点的位置矢量;ψ为叶片方位角;ζ为叶尖涡寿命角;Vindv(ψ,ζ)为涡系对控制点的诱导速度;Vextr为控制点上其他原因引起的附加速度。
根据升力面自由尾迹模型可得到翼型的叶尖涡几何形状和环量大小,基于Biot-Savart定律获得自由涡对叶片控制点的诱导速度,结合入流速度和附加速度,即可得到翼型的有效攻角以及有效入流速度,结合翼型的气动参数,可计算得到展向位置各翼型的升阻力特性,沿叶片半径积分可得到整个叶片的气动力和风轮的整体气动特性。
1.3 水动力模型
水动力作用对象是OC3-Hywind浮式平台[13],水下部分是规则的圆柱体,且直径相比波浪波长较小,属于海洋小尺度结构体,以绕流理论为基础的Morison方法较为适用。 Morison方法是假设圆柱体对波浪运动无显著影响,波浪对圆柱体的作用主要是黏滞效应和附加质量效应,忽略波浪辐射力和辐射阻尼。单位长圆柱受力f为:
(7)
式中:D为水下结构体半径;CD为黏性阻力系数,与雷诺数有关;CM为惯性力系数;ρ为海水密度;us为水流速度。
由于Morison方程具有柱体静止且竖直的局限,因此需要进行修正。设竖直圆柱体在流场中进行平动运动,在绝对坐标系下其坐标qcy为(xcy,ycy,zcy),对Morison方程进行相应的修正,x、y和z方向单位长圆柱受力分别为:
(8)
式中:CA为附加质量系数;u为x方向的水流速度;v为y方向的水流速度。
1.4 系泊力模型
浮式风力机系泊系统见图5,系泊链共3条,系泊链呈120°等角度分布,且平衡位置上仅1条系泊链位于yz平面,锚点位于y轴负方向上。

图5 系泊系统示意图Fig.5 Schematic diagram of mooring system
海洋结构体的系泊系统本质上是非线性响应,系泊力的计算主要分为准静态假设法和动态法。研究表明,准静态假设法可以准确预测Spar式浮式平台在多数情况下的等效系泊力[14],忽略了系泊链的惯性力及其在水中运动的黏性力。据海洋工程结构体的研究经验,系泊链可以简化为2种系泊链模型,一种是系泊链完全悬挂,另一种是系泊链部分悬挂,部分松弛在海底,如图6所示。其中,L为系泊链的无张力长度,ω为系泊链单位长度的折合重力,EA为系泊链的抗拉刚度,xF和zF分别为导缆孔F距离锚点A的水平距离和竖直距离,l为系泊链松弛在海底的长度,VF和HF分别为系泊链对导缆孔F的竖直系泊力和水平系泊力,VA和HA分别为锚点处的竖直拉力和水平拉力。

(a) 完全悬挂
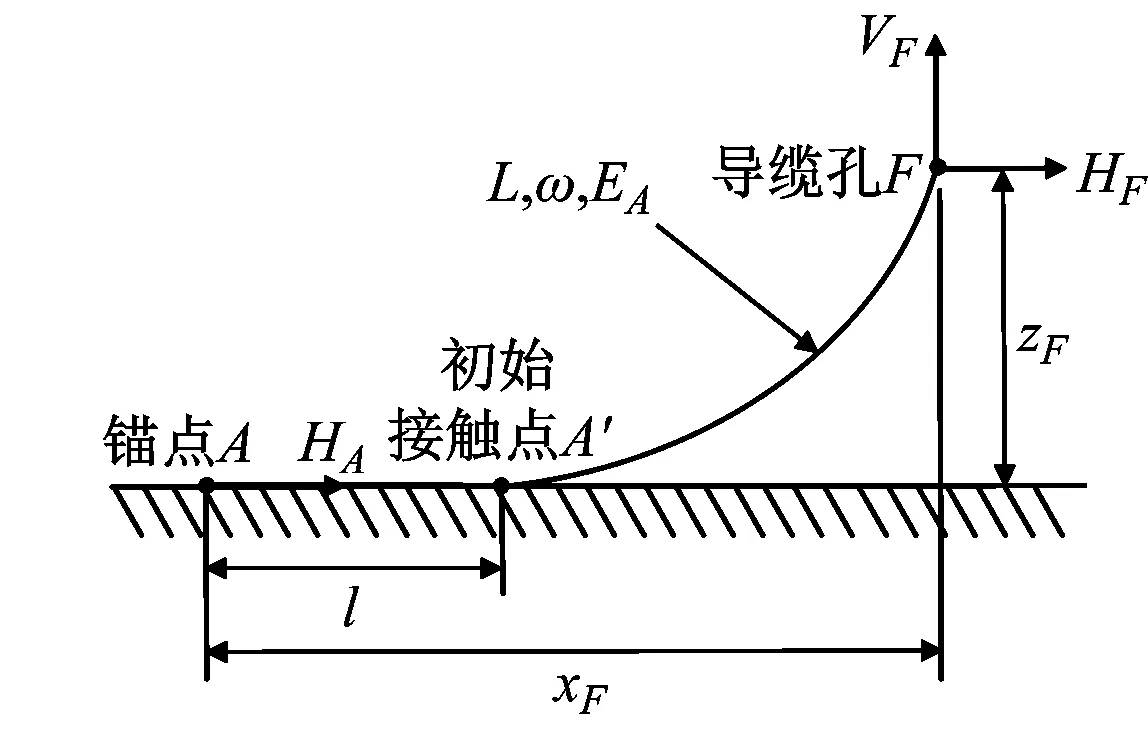
(b) 部分悬挂图6 系泊链模型Fig.6 Mooring chain model
在完全悬挂情况下,xF和zF分别为:
(9)
在部分悬挂情况下,xF和zF分别为:
(10)
1.5 时间推进全耦合算法
浮式风力机在气动力、水动力以及系泊力的作用下进行多自由度运动,该运动又反过来影响叶片上的气动力、浮式平台上的水动力以及系泊力,形成一个复杂的多因素耦合问题。为建立浮式风力机的全耦合模型,将前文所述的多体系统动力学模型、升力面自由尾迹模型、水动力模型以及系泊力模型通过广义坐标进行耦合,建立浮式风力机全耦合模型,其算法流程见图7。其中,Q″为Q的二阶导数,tmax为最大仿真时间。
在初始时刻输入浮式风力机的相关参数和外部环境条件,包括质量、几何外形、惯量、运动学参数、风力的数学描述和波浪的数学描述等,根据建立的各类模型,得到t时刻浮式风力机系统所受的气动力、水动力和系泊力,将其与浮式风力机动能一起代入式(1)中,即可得到式(11),求解得到t+Δt时刻浮式风力机的位置q和速度q′,进入下一个时间步。
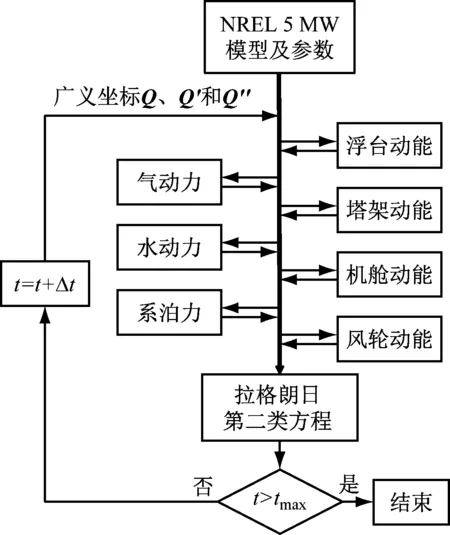
图7 全耦合算法流程图Fig.7 Flow chart of fully coupled algorithm
(11)
式中:t0为初始时刻;q0为初始时刻浮式风力机的位置。
将式(11)进行降阶后可得到一阶方程组,采用四阶显式龙格-库塔解法进行数值求解。
(12)
式中:k为中间参量。
时间步长h的四阶显式龙格-库塔形式为:
(13)
L1=f(tn,qn,kn)
在动力学方程时间步进过程中,式(11)中q的求解需要气动力、水动力和系泊力的输入,这3种力的求解又受到参数q的影响,需要解耦求解,以气动力的求解为例。
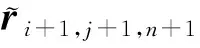
(14)
(15)
采用校正步得到的控制点位置矢量ri+1,j+1,n+1和诱导速度Vindv(ψ,ζ)分别为:
ri+1,j+1,n+1=[(24Δψ-21Δζ)ri,j+1,n-3Δζri-1,j+1,n+Δζri-2,j+1,n-(24Δψ-23Δζ)ri+1,j,n-(24Δψ+
(16)
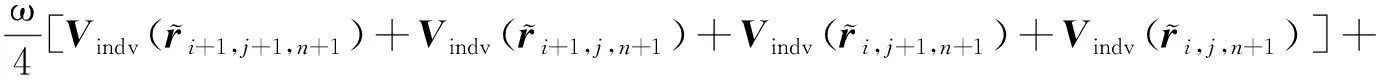
(17)
式中:Δζ和Δψ分别为叶尖涡寿命角和叶片方位角的步长。
在计算自由尾迹控制点处的诱导速度时需要结合叶片上的环量、尾迹位置以及涡量。因此,首先在预测步求解得到浮式风力机尾迹控制点上的诱导速度,再通过尾迹求解校正步,得到尾迹控制点的校正位置,最后求解校正位置处的诱导速度,得到预测校正后的气动力。
2 算例验证
2.1 Delft风轮的叶尖涡预测
Delft风轮是为测试风轮尾迹而开发的双叶片风轮。图8给出了Delft风轮在尖速比λ=8、偏航角为30°的工况下叶尖涡形状预测值与实验值[15]的对比。如图8所示,叶尖涡形状的预测值与实验值吻合良好,说明升力面自由尾迹模型能够较好地预测浮式风力机叶尖涡的发展过程,捕捉到更多的流动细节,表明所建立的气动模型能够准确预测浮式风力机的非定常气动性能。
2.2 浮式风力机的运动响应
以Spar式NREL 5 MW浮式风力机为研究对象,其详细参数见文献[13]。基于建立的全耦合模型研究该浮式风力机在不同工况下的运动响应。
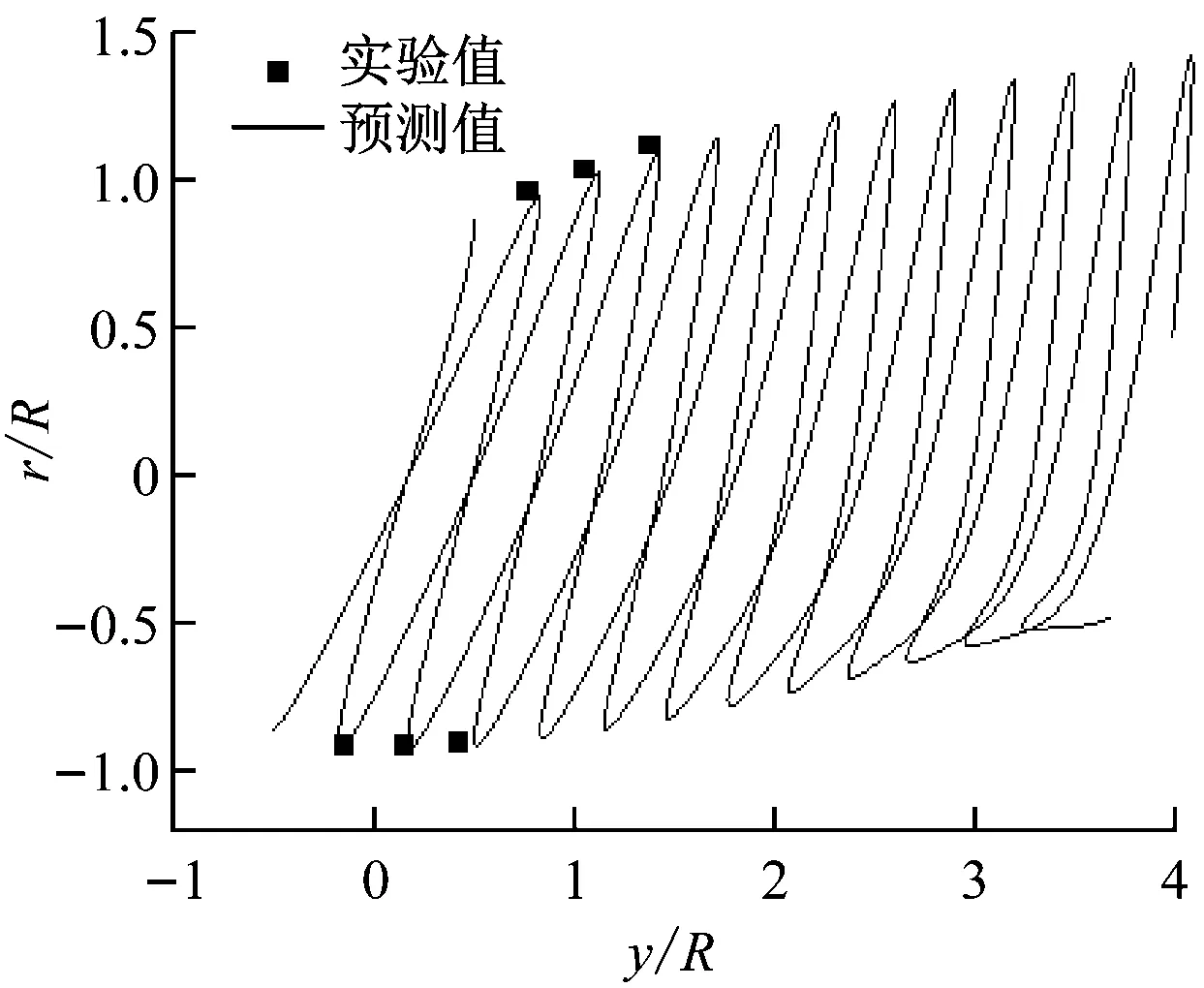
图8 叶尖涡形状预测值与实验值的对比
2.2.1 自由衰减运动
在静水无风的工况下,初始时刻浮式风力机沿y轴正方向偏离平衡位置20 m,在系泊力作用下浮式风力机进行自由衰减运动,将本文的预测结果与FAST的计算结果进行对比,结果见图9。
两者的运动轨迹几乎重合,验证了前文所述多体系统动力学模型、升力面自由尾迹模型、水动力模型以及系泊力模型的准确性,且水动力附加质量、附加阻尼以及各类回复刚度等参数的计算符合一般规律。
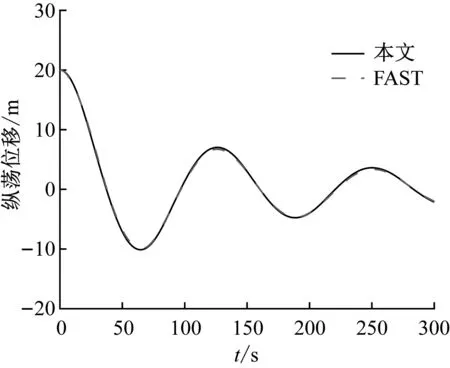
图9 纵荡运动轨迹Fig.9 Trajectory of surge motion
2.2.2 波浪作用下的受迫运动
在初始时刻,将波浪作用在处于平衡位置的浮式风力机系统上,采用Airy波描述波浪,波高为6 m,周期为10 s,从y轴正向入射;风速为0 m/s,浮式风力机转速为0 r/min。浮式风力机受到水动力与系泊力的联合作用,在水动力作用下进行多自由度的受迫运动,其运动轨迹见图10。从图10可以看出,仅在波浪作用下,在0~400 s的起振阶段,浮式风力机运动幅度较大,且呈现出较为明显的固有频率特征;400 s之后运动逐渐趋于稳定,能量集中在y方向上,即纵荡和纵摇运动,运动幅度分别约为1 m和1°,其特征频率与波浪频率相同。

(a) 平动位移
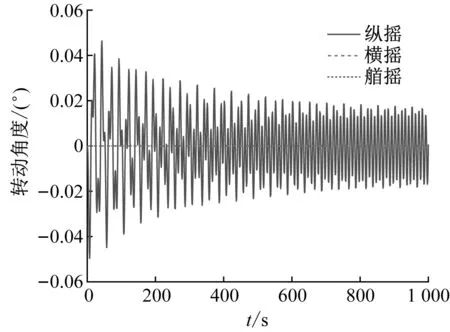
(b) 转动角度图10 波浪作用下浮式风力机的运动轨迹
2.2.3 风波联合作用下的耦合运动
在波浪作用600 s时刻,给浮式风力机系统附加定常风,风速为11.4 m/s,与波浪同向,风轮转速为12 r/min。浮式风力机在风波联合作用下的运动轨迹见图11。由于风波联合作用,浮式风力机部分动能从y方向传递到z方向上,发生了显著的艏摇运动。这说明所建立的全耦合模型能较好地预测浮式风力机系统的气动-水动耦合效应。

(a) 平动位移
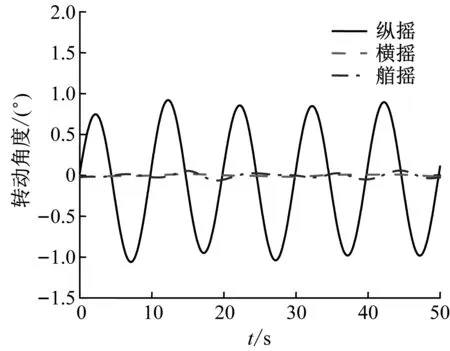
(b) 转动角度图11 风波联合作用下浮式风力机的运动轨迹
如图12所示,在风波联合作用下,浮式风力机的功率在固定功率上下浮动,平均功率减小0.22%,功率波动幅值约为2 500 kW。
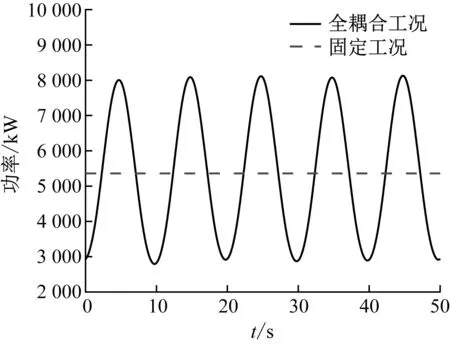
图12 风波联合作用下浮式风力机的功率变化
3 结 论
(1) 所建立的全耦合模型能够较为准确地预测浮式风力机叶尖涡轨迹,捕捉到更多的流动细节。
(2) 相同工况下,基于本文全耦合模型预测得到的浮式风力机运动轨迹与FAST的计算结果吻合良好,验证了全耦合模型的准确性。
(3) 在风波联合作用下,气动-水动耦合效应将会导致浮式风力机出现较为明显的艏摇运动。
