考虑制造商行为的双渠道供应链演化博弈分析

阿布都热合曼·卡的尔 王嘉欣

（1.新疆财经大学 信息管理学院，新疆 乌鲁木齐 830011；2.新疆财经大学 统计与数据科学学院，新疆乌鲁木齐 830011）

一、引言

许多制造商为了获得额外零售利润和更大的市场占有率，选择开通网络直销渠道。5G时代的来临使信息传播的速度加快，信息传播面飞速扩展，所以许多制造商选择投入广告来提升客户需求、增加销量、开拓市场。

目前，学者的研究集中于广告在闭环供应链中的影响。Ningning Wang和Ting Zhang等[1]建立了一个制造商和两个竞争零售商组成的双渠道供应链模型，对其中的三种广告策略和三种模式进行研究。结果表明，联合广告对参与者有利。高举红和张莹等[2]人发现利润较高的新产品会受到再制造品的影响，所以要对新产品的广告投入制定合适的广告策略。结果发现，制造商主导模式对经济效益更有益。Xiang Li和Yongjian Li等[3]研究了由销售商和在线平台代理组成的O2O供应链中的合作广告策略。最终给出了三种模式的比较结果，发现双边合作广告模式与单边合作广告模式相比，能够给卖家和整个渠道带来显著的利益。Zhanbing Guo和Junhai Ma[4]研究了非线性动态系统理论应用于供应链中的合作广告模型，将企业的决策机制建模为动态调整过程，并假设广告响应为指数函数。最终的研究结果对合作广告项目和具有指数需求函数的动态博弈的特征提供了一些有价值的见解。姚锋敏和刘珊等[5]研究第三方回收闭环供应链定价策略受不同广告模式的影响。研究表明，不管在任何广告模式下，和主导零售商及制造商相比，第三方回收商的利润总是最小。Yuyan Wang和Zhaoqing Yu[6]构建了三种电子供应链运作模式，并对这些模式下的最优定价策略和广告策略进行了研究和比较。结果表明，销售价格、网络平台服务水平、广告投入以及厂商、网络平台和电子供应链的利润都随着广告刺激需求增长而增加。Haitao Chen和Zhaohui Dong等[7]建立了两个阶段的供应链模型，即广告模型和联合模型，对闭环供应链中的定价策略和广告决策这两种营销策略的经济和社会绩效进行分析和比较。结果发现影响厂商利润和社会福利总额的关键因素是市场需求的广告弹性。Qingyun Xu和Bing Xu等[8]研究了两阶段供应链中各渠道成员的最优广告投放力度和零售商竞争下制造商的补贴策略，研究表明，在竞争效应较小的情况下，双边参与契约可以实现供应链的协调，增加零售商参与该契约的可能性。许民利和郭爽等[9]建立了制造商广告和零售商广告两种模型，并对其供应链决策进行研究。最终发现，广告效应可以有效地提高需求量和回收率。Razieh Shoeleh和Mehdi Seifbarghy等[10]研究了由一个供应商、一个制造商和一个零售商组成的三级供应链中，价格和质量水平作为附加决策变量的问题。结果表明，制造商在纳什博弈中更倾向于与零售商和供应商进行Stackelberg博弈，而不是与零售商和供应商发生冲突。Yi He和Hang Wang等[11]研究了由单个制造商和单个零售商组成的两阶段供应链中的合作广告策略。研究发现：（1）制造商在同一时期通常不会对两代产品提供相同的广告补贴策略；（2）如果广告的长期效应较强，制造商可能会向零售商提供较低的补贴率。Yang Qing[12]研究了供应链中合作广告策略的选择与优化问题。得出供应链中各企业在横向合作广告水平下的最优合作广告策略获得链。Wenhui Li[13]建立了一个具有网络外部性的两阶段博弈模型，研究发现两阶段博弈中的最优选择是实现充分合作。Peter E Ezimadu和Chukwuma R Nwozo[14]研究制造商-零售商供应链中的合作广告。研究表明，制造商的广告投入随着补贴的增加而减少，而零售商的广告投入和产品知名度则增加。这些结果导致所有玩家的收益增加。Dan Xiao和Yong-Wu Zhou等[15]研究了供应链成员之间的广告合作问题。结果表明每个博弈的核心都是非空的。Amir Ahmadi-Javid和Pooya Hoseinpour[16]研究了制造商-零售商供应链中的合作广告。研究表明当生产能力不受限制时，可以证明几个重要的性质，而这些性质对于现有的销售功能是无法用解析的方法表示的。Fan Yang[17]建立了一个由零售商和零售商组成的简单二级供应链制造商。研究发现生产能力的缺乏使得制造商没有主动分担零售商的广告成本。但当生产能力足够时，广告费用由制造商分担1/3。此外，无论是制造商还是零售商在小产能的情况下选择合作，供应链的利润都不会改变。Yong-Wu Zhou和Jicai Li等[18]研究了两级供应链中制造商通过风险规避零售商销售产品的合作广告和订货问题。研究发现：如果集中供应链的决策者比分散供应链的两个参与者更具风险规避能力，集中供应链在许多情况下可能表现得比分散供应链差；在分散的背景下，领导者比跟随者更厌恶风险，对两个代理都更有利。Pan Liu和Shu-Ping Yi[19]选择了一个绿色制造商和一个零售商的绿色供应链。结果表明，最优零售价格和批发价格与目标广告的绿色度和投入水平呈负相关。Juan Zhang和Qinglong Gou等[20]建立了一个同时包含参与率和应计率的单制造商-单零售商供应链动态合作广告模型。结果表明，由于收益率的存在，参与率的增加并不一定会增加零售商的广告投入。

回顾国内外的文献可以发现，关于闭环供应链的研究很多基于合作模式的多渠道供应链价格博弈。在信息时代，消费者的信息接受面日益广泛，制造商的广告宣传努力会直接影响消费者购买行为。本文考虑制造商投入广告情况下，研究制造商广告努力水平对零售商和制造商最优决策和利润的影响。由于供应链管理系统是非线性系统，各节点企业间的关系是一个长期且复杂的过程，需要反复多次进行博弈。鉴于此，本文将制造商投入广告成本引入到双渠道供应链中，分别建立静态模型和动态模型下供应链决策模型。本文的贡献在于：（1）研究了投入制造商广告成本行为对定价的影响，以探索投入广告行为是否会影响决策主体的定价策略，能否提升低碳供应链系统的利润；（2）对双渠道供应链中价格决策和广告投入水平的长期动态博弈行为进行演化分析，为制造商和零售商等决策主体在面对供应链系统混沌时所做出的策略提供理论依据。

二、模型的建立

考虑制造商投入广告，由制造商和零售商构成的双渠道供应链。其中制造商是Stackelberg博弈的领导者，专业零售商是追随者。制造商负责新产品的生产并且通过网络直销新产品，专业零售商也销售新产品。制造商为了使自己获得较高的利润和保持市场平衡，更好地发挥在市场上的主导作用，减少渠道间的冲突，除了决定自己的直销价格外，还需要考虑专业零售商的利润和价格。在产品销售过程中，制造商会通过投放广告宣传产品，专业零售商市场会受到广告的影响。模型如图1所示。

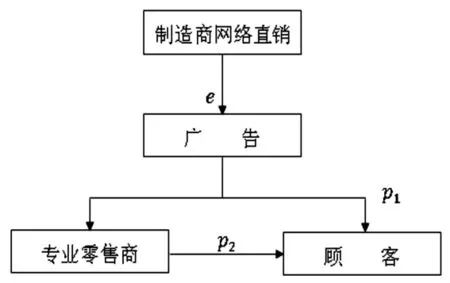
图1 广告投放下的双渠道供应链模型

1.模型假设

对模型的研究进行如下假设：

（1）制造商和专业零售商向消费者出售完全相同的产品，只通过改变自身价格进行竞争，其竞争规则符合柏川德模型。

（2）制造商和专业零售商都不能完全掌握市场信息，因此都采用有限理性的价格决策方式。

（3）制造商在市场上占主导地位，决定直销价格的同时会考虑专业零售商的价格和利润。

（4）制造商和专业零售商进货渠道相同，产品没有固定成本，产品成本就是单位可变成本。

（5）消费者对产品的需求是线性的，需求量随销售价格的升高而减少。

（6）在闭环供应链中，制造商和零售商都是独立决策者，在离散的周期点 t=0，1，2，3，4，…，分别进行决策，都以自身利润最大化为决策目标，但由于市场条件的约束，它们不能完全掌握其他决策者的行为和市场状况，所以只能采用有限理性决策。

2.符号说明

a1：制造商直销面对的潜在最大市场需求。

a2：专业零售商面对的潜在最大市场需求。

当价格为0时市场对于其对应产品的需求总量。

b1：制造商直销价格影响因子。（b1＞0）

b2：专业零售商价格影响因子。（b2＞0）

每单位价格变动对需求量的影响。

d1：制造商直销竞争影响因子。

d2：专业零售商竞争影响因子。

零售商每变动一单位的价格对另一个零售商需求的影响。

s1：制造商投入广告对制造商直销的影响因子。

s2：制造商投入广告对专业零售商的影响因子。

制造商广告努力程度每单位价格变动分别对两零售商市场需求的影响。

p1：制造商网络直销价格。

p2：专业零售商零售价格。

h：广告成本影响因子

每单位广告努力投入下企业需要付出的成本。

e：制造商的广告努力程度。

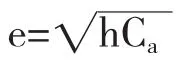
Ca=he2（0＜h＜1）

q1：制造商面对的市场需求量。

q2：零售商面对的市场需求量。

基于以上变量假设，本文考虑如下两个线性需求方程：

考虑广告努力水平对市场需求的线性影响关系。se正是体现对这一点的考虑。

c：制造商网络直销和零售商的成本函数。

制造商直销的利润函数：

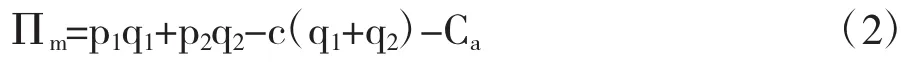
v∈（0，1）—价格调整偏好系数。

每单位广告努力投入下企业需要付出的成本。

专业零售商对于实际价格和最优计算价格差异的敏感程度，因为市场竞争中专业零售商应对制造商直销渠道，当v较大时，说明零售商希望通过价格的调整，尽快达到最优价格，以获得更大的利润。

专业零售商的利润函数：

公式（1）带入公式（3）和（4），可以获得系统利润函数：

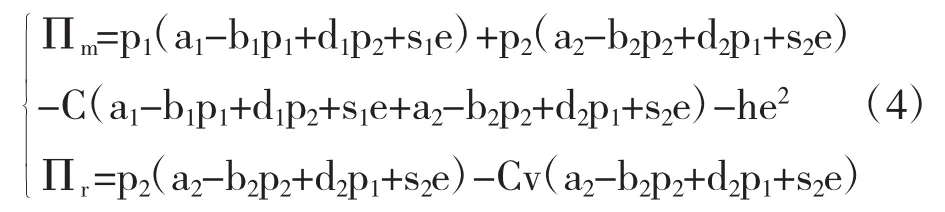
由（4）可以看出制造商的决策变量为制造商直销价格p1和广告成本e，零售商的决策变量为零售价格p2，由此得到的边际利润函数为：

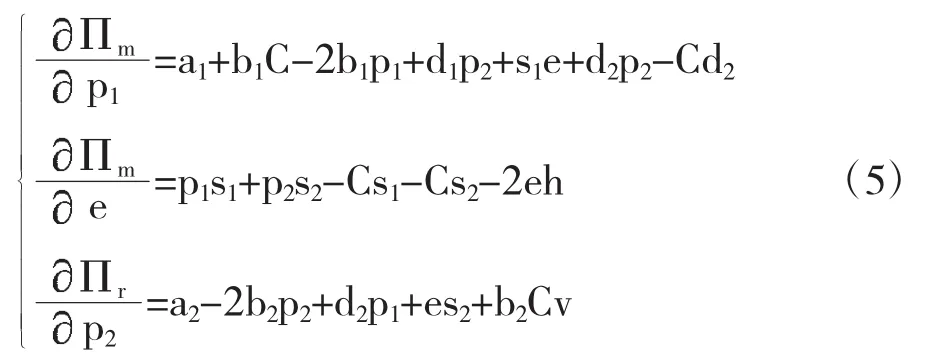
由于市场纷繁复杂，制造商、零售商得到的信息都是有限的，因此是有限的理性，在这种假设下，t+1时刻的决策方式为：

其中 vi＞0（i=1，2，3）分别表示制造商对于其网络销售价格p1，广告成本e以及零售商对于其销售价格p2的调整速度。它们通过改变价格调整速度来获取市场优势，以便获取更大的利润，将公式（5）带入公式（6）就得到了制造商网络直销渠道和专业零售渠道组成的双渠道供应链价格博弈三维动力系统。

3.模型分析

根据模型（7）动力系统求得系统的均衡点为：

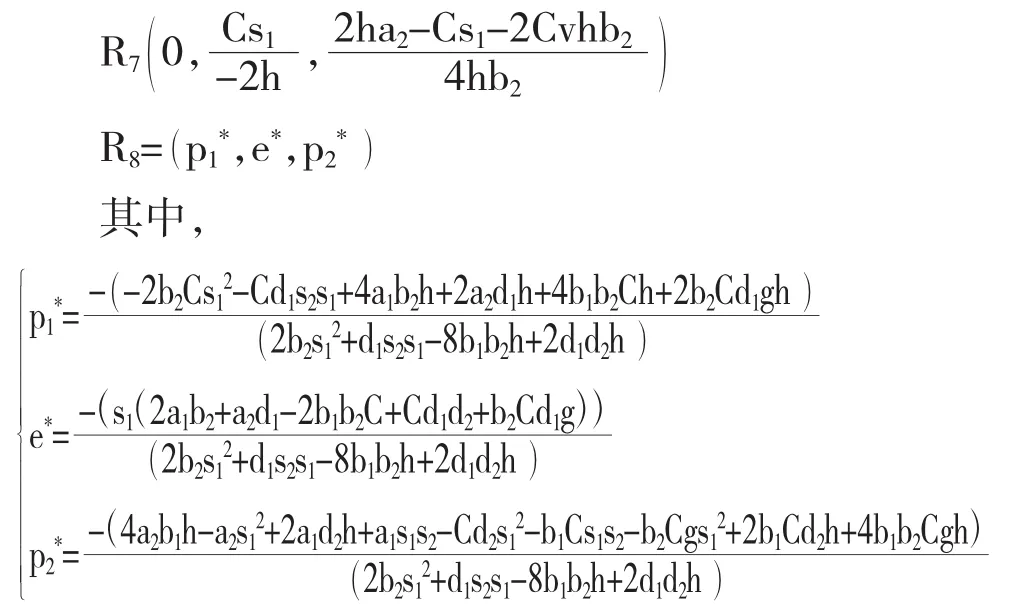
以上8个均衡点，只有R8是完全非零的，而R1—R7的均衡解均不完全非零，在经济学中，决策者不会选择零值的决策变量，R1—R7都是不稳定的，只有R8是局部稳定。下面通过求解各个均衡解的Jacobian矩阵来加以验证。

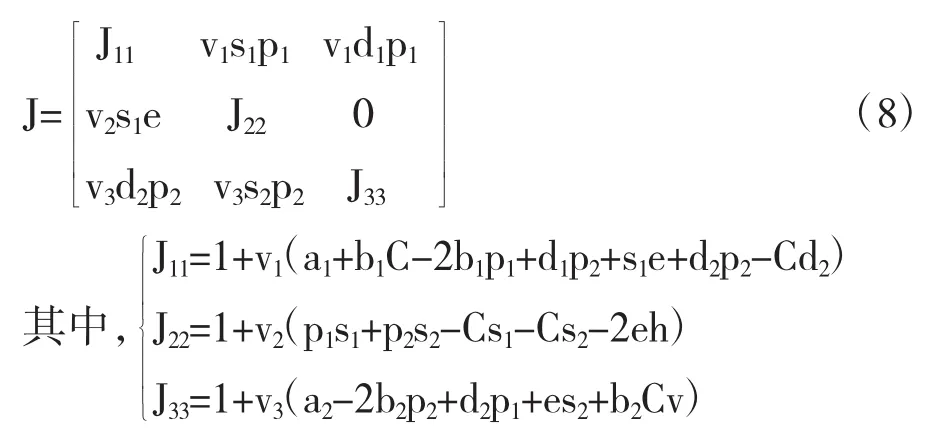
三、数值模拟

数值模拟可以全面地展示系统的稳定性和参数对系统的作用。在此进行数值仿真模拟，对系统中各参数赋值：a1=10，a2=10，b1=2，b2=2，d1=0.2，d2=0.2，c=0.2，s1=0.8，s2=0.7，h=0.4，g=0.01。对参数赋值后，利用Matlab绘制系统的分叉图、最大Lyapunov指数图来分析系统的混沌状况。

当v2=0.01，v3=0.01，v1的取值在0到0.1484时，其中vi＞0（i=1，2，3）为价格调整速度。最大Lyapunov指数小于零，系统处于稳定状态。制造商网络直销的价格为3.397的唯一纳什均衡解。v1等于0.1485时，制造商网络直销价格出现倍周期分岔的现象，由唯一均衡解变为两周期均衡解，最大Lyapunov指数等于0。当v1逐渐大于0.1845时，制造商网络直销价格发生第二次分岔，变成四周期均衡解。p1随着调整速度的增加逐步进入混沌状态，最大Lyapunov指数大于0。如图2所示。

图2 制造商网络直销价格随v1变化的动态演化图

当v1=0.15，v3=0.15，v2的取值在0到0.009时系统是稳定状态，此时最大Lyapunov指数小于零。制造商投入广告成本为3.098的唯一纳什均衡解。当v2等于0.009时，制造商广告成本出现倍周期分岔的现象，由唯一均衡解变为两周期均衡解，最大Lyapunov指数等于0。当调整速率大于0.53时，制造商广告成本发生第二次分岔，变成四周期均衡解。e随着调整速度的增加逐步进入混沌状态，最大Lyapunov指数大于0。如图3所示。

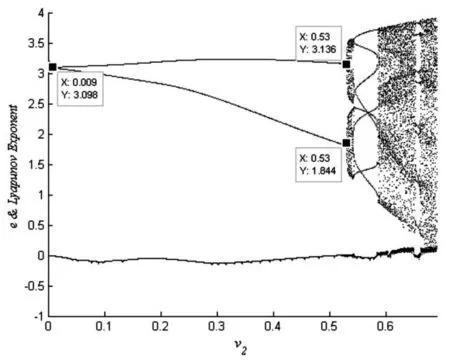
图3 制造商投入广告成本随v2变化的动态演化图

当v1=0.11，v2=0.11，v3的取值在0到0.1583时系统处于稳定状态，最大Lyapunov指数小于零，系统处于稳定状态。专业零售商的价格为3.247的唯一纳什均衡解。当v3等于0.1583时，专业零售商价格出现倍周期分岔的现象，最大Lyapunov指数等于0。由唯一均衡解变为两周期均衡解。当调整速率大于0.1897时，专业零售商价格发生第二次分岔，变成四周期均衡解。p2随着调整速度的增加逐步进入混沌状态，最大Lyapunov指数大于0。如图4所示。

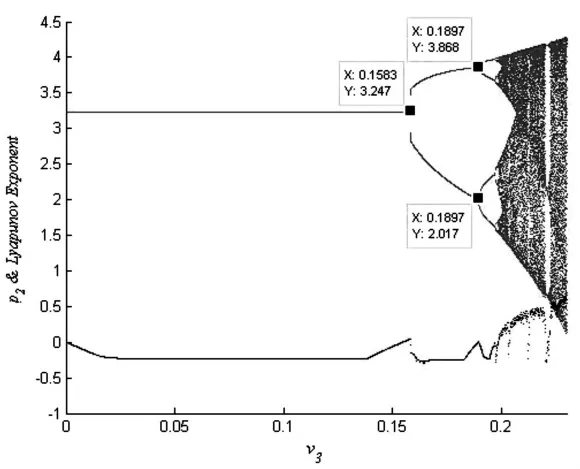
图4 专业零售商价格随v3变化的动态演化图

通过图5和图6可以发现，v1和v3在变化时，系统的分叉点不同，v1在到达0.1485时，系统产生分岔，而v3在到达了0.1583时，系统才产生分岔，v3的分岔点要比v1靠后，这说明制造商在调整直销价格时，由于不仅会影响到自身销售数量，还会对零售商的零售决策造成影响；而零售商调整零售价格时，由于对于制造商没有过大的影响，但会很大程度上影响自身的销售量，所以相比之下，制造商直销价格的调整要比零售商对于自身零售价格的调整对于整个系统具有更大的影响力。

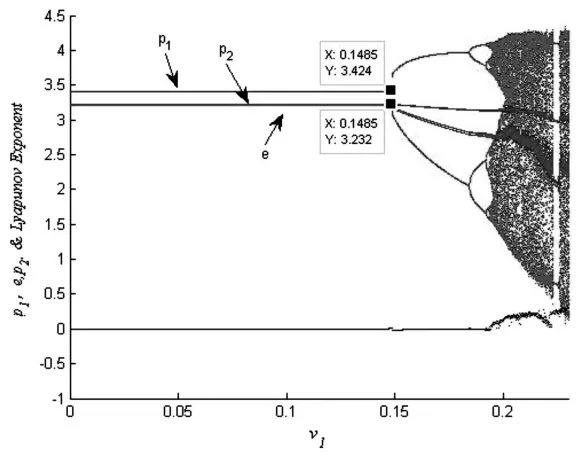
图5 v1变化的动态演化图

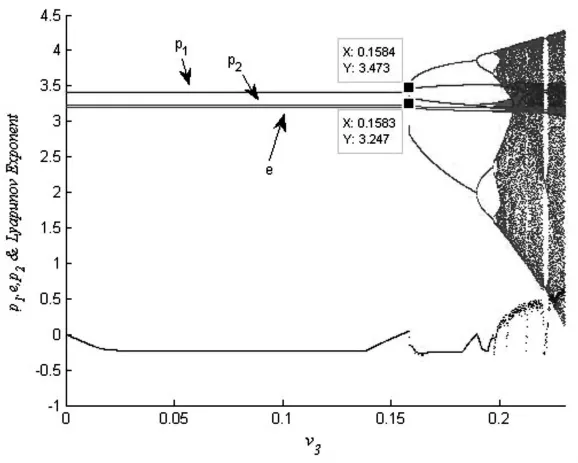
图6 v3变化的动态演化图

还可以发现，不管调整速度怎么变化，专业零售商的价格一直低于制造商直销的价格。一方面是因为制造商需要承担广告成本的费用，而专业零售商可以直接享受制造商投入广告所带来的利益。另一方面是由于专业零售商相对于制造商来说属于跟随者，如果定价超过制造商，可能会造成产品滞销。随着专业零售商价格决策变量值不断增加，在市场上表现为价格稍微提高，最终都会导致市场的混沌无序。制造商通过网络直销具有电子商务便捷的优势，专业零售商可以通过提升售后服务，增加顾客的体验等方式使自己更有竞争力。

四、混沌控制

通过数值模拟发现调节参数会对系统的稳定性产生很大影响，导致系统分岔并陷入混沌状态。对于本文的研究模型来说，混沌意味着制造商网络直销价格和专业零售商价格都不稳定，最终使产品市场陷入混乱，制造商和专业零售商都会遭受严重的经济损失。因此，采用参数调整的方法对处于混沌状态下的系统进行控制，使其逐渐恢复到稳定状态。

未进行控制的动态离散系统可以表示为：

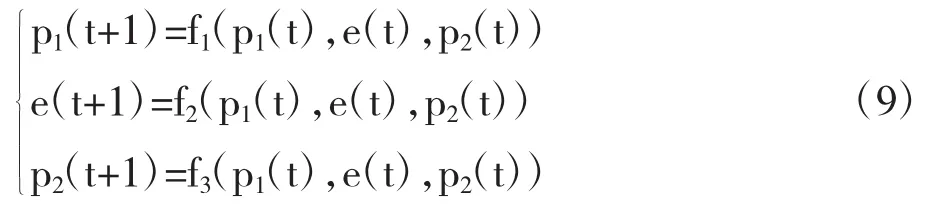
对其进行参数调整后，控制系统可以表示为：

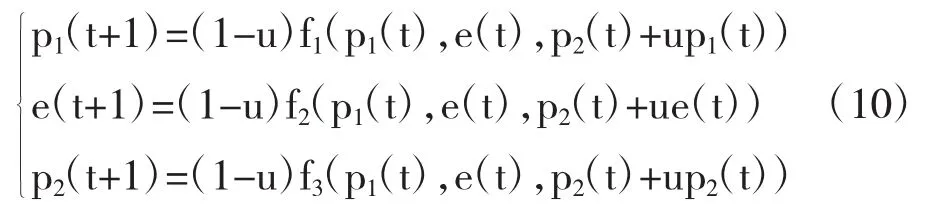
控制系统（10）中u为调整参数，其中：0＜u＜1。我们可以通过调整参数u的值来控制系统混沌现象的发生。采用数值模拟的方式，当v1=0.1，v2=0.1，v3=0.001时，系统处于混沌状态，加入调节参数u以后，随着调节参数的变化，3个变量都由混沌状态逐渐趋于稳定状态。图7是系统随着控制参数u变化的价格分岔图和最大Lyapunov指数图，图中可以看出控制参数u大于0.223时系统从混沌状态回到稳定状态，表明制造商网络直销价格和专业零售商的价格重新趋于稳定。可能是政府为了市场经济的稳定，进行外部调节导致控制参数u的变化。也可能是制造商和零售商发现这种竞争方式对于双方都没有好处，所以为了延迟或消除混沌，制造商和零售商主动联合起来，对混沌采取控制措施。

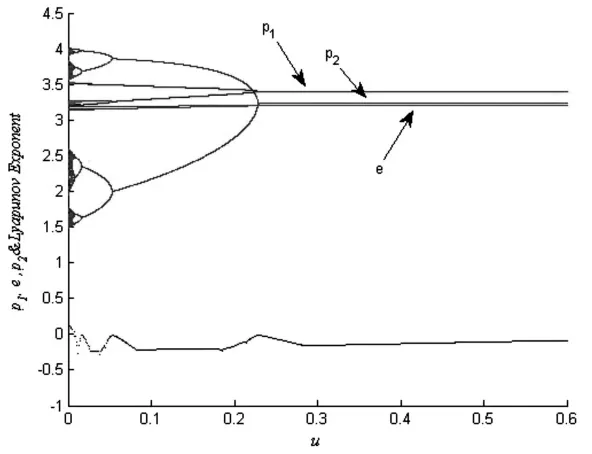
图7 随调节参数u变化的分岔图

五、结论

本文考虑制造商投入广告成本，制造商和专业零售商组成的双渠道供应链，在建立双渠道供应链静态和动态模型的基础上，利用Matlab对系统的长期价格博弈进行数据模拟，综合判定了系统的复杂动力学特征。研究了各个渠道的价格决策变量的长期演化对市场稳定性的影响，最后进行了相应控制。研究结果表明：第一，零售商和供应链的利润随制造商投入广告努力程度的加大而增加。第二，市场会随着制造商网络直销价格和专业零售商的价格调整速度加快进入混沌无序的状态，导致无法预测制造商和专业零售商的利润。第三，通过系统分岔图、最大Lyapunov指数的变化，发现市场受双方的价格调整速度的影响较大。但是专业零售商的影响相对较小，进入混沌时期比较晚，稳定期长，价格偏高。第四，从分岔图中可以看出，专业零售商的价格始终低于制造商网络直销的价格，随着价格调整速度加快，短时间内可以带来价格提升，但还是低于制造商网络直销的价格，逐渐导致市场进入混沌状态。因此专业零售商除调高价格以外，还应该考虑其他方法来增加利润。比如可以通过提升产品体验和强化售后服务等方式提高利润。第五，制造商和专业零售商合作对市场进行混沌控制，可以有效地将系统的混沌状态延迟或消除。◆