基于多源遥感数据的城市交错带约束布局优化
2021-11-17王晓燕
陈 莉,王晓燕
(宁夏大学土木与水利工程学院,宁夏 银川 750021)
1 引言
受城市化进程加快的影响,城市空间范围扩张速度增加[1-2]。生态环境污染、土地盲目利用、城市建设混乱导致人居破碎化程度日益加剧[3-4],为了高效利用土地,需要对城市交错带进行优化布局[5]。
叶菁等[6]提出基于生态承载力的交错带布局优化方法,该方法在市域范围内通过状态空间法评价土地承载力,采用三维魔方方法建立国土空间开发格局与生态承载力评价的关联模型,根据关联模型分析城市交错带布局特点,实现城市交错带的布局优化,该方法没有分析交错带空间结构,导致总体精度低、Kappa系数低。许小亮等[7]提出基于CLUE-S模型的城市交错带布局优化方法,该方法在不同情境下采用非线性优化模型分析土地利用结构,通过Logistic回归模型获取交错带的优化布局,利用CLUE-S模型将交错带优化数量作为约束,对交错带布局进行优化,该方法没有分析城市交错带功能与结构之间存在的关系,优化城市交错带布局所用的时间较长,存在优化效率低的问题。曹巍等[8]运用田园综合体、休闲农业及景观规划学中涉及的相关理论知识,提出田园综合体模式的江头贡茶生态休闲农庄规划设计总体构架,并结合江头贡茶生态休闲农庄田园综合体新理念,打造江头贡茶农庄田园综合体建设示范区,但是其实地限制性太强,应用范围较窄。
为了解决上述方法中存在的问题,提出基于多源遥感数据的城市交错带约束布局优化方法。其创新之处在于在景观格局指数的基础上构建城市交错带约束布局优化模型,并采用粒子群算法进行求解,获得模型最优解实现城市交错带的布局优化。
2 多源遥感数据采集
2.1 多源遥感数据处理
1)几何校正
获取遥感图像时容易产生误差和几何畸变,需要对遥感图像进行几何校正。运载器或传感器在姿态和性能上的差异造成物体存在差异是产生几何畸变的主要原因。基于多源遥感数据的城市交错带约束布局优化方法采用最近邻重采样法和三次多项式拟合方法处理多源遥感数据中存在的误差,实现遥感图像的几何校正。
2)辐射定标
利用定标参数offset和gain确定表现反射率和辐射亮度值的计算公式
L=Gi×DN+ot
(1)
式中,DN表示遥感图像像元对应的亮度值;L表示光谱辐射亮度。
2.2 景观格局指数
采用基于多源遥感数据的城市边缘带约束布局优化方法,可以根据获得的多源遥感数据选择和计算景观格局指数。
景观格局指数可以分析城市边缘区功能结构与城市边缘区空间结构的关系,为城市边缘区的优化布局提供相关信息。
单个景观要素通常是由不同形状和大小的斑块组成,它能反映生态因子对格局的影响、景观空间变化、景观要素之间的关系以及景观要素的特征。
1)平均斑块形状指数
斑块形状对物质、能量、物种在景观中的运移、流动和扩散情况具有重要意义。景观要素斑块的边缘复杂程度和规则程度可以通过平均斑块形状指数MSI进行反映,平均斑块形状指数MSI的计算公式如下

(2)
式中,m表示景观类型总数;Ek表示斑块在景观类型k中对应的周长;Ak表示景观类型的面积。平均斑块形状指数可以表示斑块与正方形之间的相差程度,当斑块接近于正方形时,平均斑块形状指数的值越接近1。平均斑块形状指数值越大,面积有效性越小、边缘地带越大、边界越复杂,斑块在景观中的形状就越不规则。
2)斑块密度
设PD表示斑块密度,可以对景观空间异质性程度和景观破碎化程度进行反映,斑块密度PD的计算公式如下

(3)
式中,ni表示某类斑块在景观中的数量。空间异质性程度和破碎化程度随着斑块密度的增大而增大。
3)平均斑块分维数
景观斑块周围形状的复杂程度可以通过斑块分维数进行衡量,平均斑块分维数MPFD的计算公式如下

(4)
式中,N表示景观中存在的斑块总数;aij表示斑块ij对应的面积;pij表示斑块ij对应的周长。平均斑块分维数在区间[1,2]中取值,斑块形状越复杂,平均斑块分维数越靠近2,斑块形状越简单,平均斑块分维数越靠近1。
4)空间质心
空间中斑块的转移规律可以通过斑块空间质心的变化进行表示。设(xt,yt)表示空间质心坐标,可通过下述公式计算得到

(5)
式中,Cti表示第i个斑块在第t年的面积;Xi、Yi表示第i个斑块质心在经纬度坐标系下对应的坐标。
5)景观多样性指数
设H表示景观多样性指数,可以对景观元素类型的均匀程度、丰富程度以及优势性程度进行表示,其计算公式如下
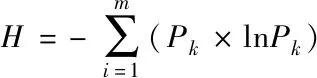
(6)
式中,Pk表示景观类型k在整个景观中的面积比例。
6)景观优势度指数
景观优势度指数D可以对景观镶嵌体支配景观格局的程度进行反映,在景观中景观优势度指数D属于重要指标,其主要目的是在景观中测试嵌块体的重要性,景观优势度指数D的表达式如下

(7)
偏离程度随着景观优势度指数的增大而增大。
7)景观破碎化指数
景观斑块的复杂程度可以通过景观破碎化程度指数进行衡量,与景观过程、功能和格局密切相关。当景观斑块破碎化指数为1时,表明景观完全破碎,当景观斑块破碎化指数为0时,表明景观无破碎化存在,景观破碎化指数的计算公式如下

(8)
式中,FN1表示研究区域的整体景观破碎度指数;Np表示各类型斑块在景观中的总数;Nc表示景观·总面积与斑块最小面积之间的比值;FN2表示各类景观对应的破碎度指数;MPS表示各类斑块在景观中的平均斑块面积与斑块最小面积之间的比值;Nf表示某类景观在整体景观中的总数。
8)景观边缘密度
设ED表示景观边缘密度,其计算公式如下
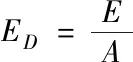
(9)
式中,A表示景观总面积;E表示斑块在景观中对应的边缘长度。景观边缘密度是景观斑块密度和斑块形状的函数,可以反映异质斑块之间在景观中的互相影响强度以及物种、能量和物质信息的交换潜力。
3 城市交错带约束布局优化
3.1 城市交错带约束布局优化模型
基于多源遥感数据的城市交错带约束布局优化方法根据景观格局指数以用水目标、生态目标和经济目标为优化方向,构建城市交错带约束布局优化模型。
经济目标函数的主要目的是最大化经济收益,经济目标函数的表达式如下
maxf1=maxC1Xk
(10)
式中,Xk表示区间数向量,由土地面积变量构成;C1表示土地单位面积产值构成的区间数向量。
生态目标函数的主要目的是在保护生态环境的基础上,促进地区可持续发展,最大化经济收益,生态目标函数的表达式如下
maxf2=maxC2Xk
(11)
式中,C2表示专家打分结果,评价生态环境受土地利用方式的影响。
在城市交错带约束布局优化过程中,如果不节约用水,会导致水资源紧缺,用水量目标函数的表达式如下
minf3=d1+d2
(12)
式中,d1表示相对于目标水量,用水量的正偏离;d2表示相对于目标水量,用水量的负偏离。
利用上述子目标函数,构建城市交错带约束布局优化模型F
F=maxf1+maxf2+minf3
(13)
3.2 模型求解
基于多源遥感数据的城市交错带约束布局优化方法采用粒子群算法对城市交错带约束布局优化模型求解。
在城市交错带约束布局优化过程中,根据重心利用图斑将土地抽象为粒子,编码粒子,编码过程包括地类k和位置(x,y)两个变量。
设定粒子群算法中存在的参数,包括学习因子c1、c2;粒子数目n;x、y方向中粒子的最大飞行速度vxmax、vymax;最大迭代次数Imax和自适应惯性权重w,权重w的主要目的是维持局部搜索能力和全局搜索能力的平衡,其计算公式如下
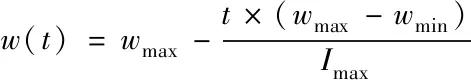
(14)
式中,wmax表示惯性权重的最大值;t表示最大迭代次数;wmin表示惯性权重的最小值。
对每个粒子对应的速度和位置进行初始化处理,使搜索空间中均匀的分布粒子,利用下述公式表示粒子对应的初始位置
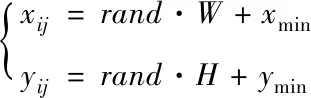
(15)
式中,xij、yij为x、y方向的坐标;rand为[0,1]区间内存在的随机数;W表示二维空间对应的宽度;xmin表示x坐标的最小值;H表示二维空间对应的高度;ymin表示y坐标的最小值。
粒子初始化飞行速度通过下述公式进行计算
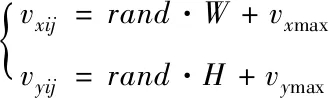
(16)
式中,vxmax、vymax表示在x轴和y轴方向粒子对应的最大控制速度。
结合空间紧凑度Aβ、规划转换可达性Cτ和地类相邻协调性Bφ约束目标构建适应度函数
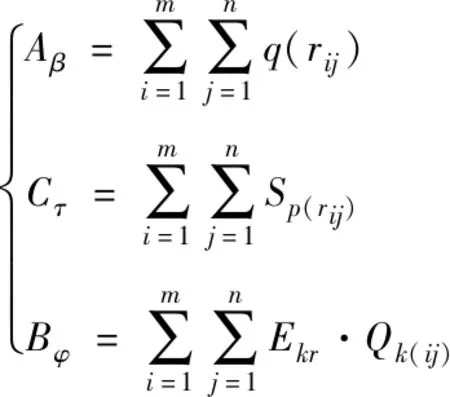
(17)
式中,q(rij)表示栅格单元中存在的单元总数;Sp(rij)表示栅格单元对应的适应度等级;Ekr表示协调性指数;Qk(ij)表示栅格数量。
为了避免粒子飞行速度过大导致的无序状态,需要设定约束条件
vx(y)=vmax,ifv>vmax
(18)
当粒子满足约束条件时输出城市交错带约束布局优化模型的最优解,实现城市交错带约束布局优化。
4 实验结果与分析
为了验证所提方法的整体有效性,需要在Simulink平台中对所提方法进行测试。分别采用基于多源遥感数据的城市交错带约束布局优化方法(方法1)、基于生态承载力的交错带布局优化方法(方法2)和基于CLUE-S模型的城市交错带布局优化方法(方法3)进行测试,将总体精度POA和Kappa系数作为测试指标,两个系数越高,表明城市交错带的布局效果越好,总体精度POA和Kappa系数的计算公式分别如下
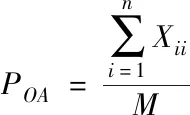
(19)

(20)
式中,M表示用于交错带布局的景观数量;Xii表示景观在误差矩阵中的数量;Xi+、X+j分别表示景观在第i行和第j列中的数量。
不同方法的总体精度POA和Kappa系数测试结果分别如图1、图2所示。
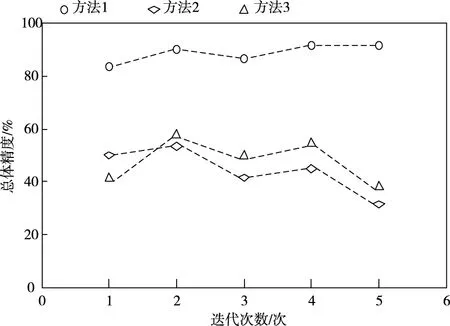
图1 不同方法的总体精度
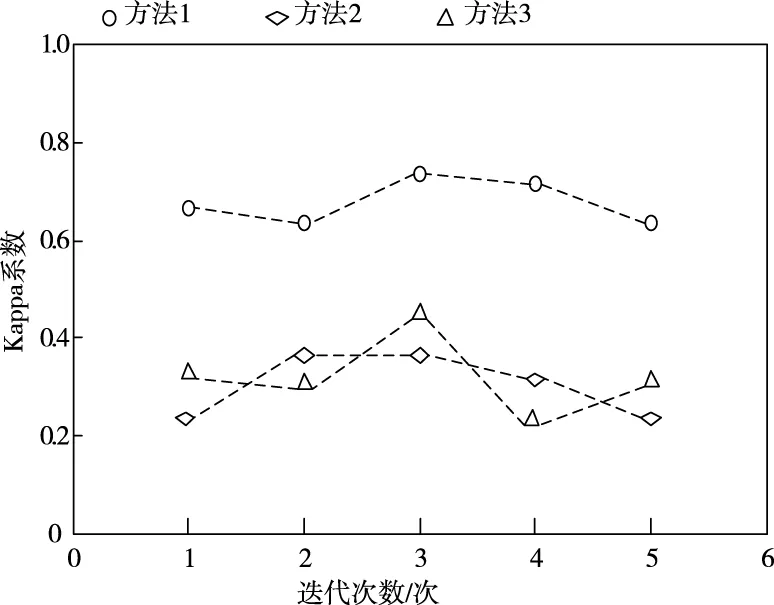
图2 不同方法的Kappa系数
分析图1和图2中的数据可知,方法1在多次迭代中获得的总体精度和Kappa系数均高于方法2和方法3获得的总体精度和Kappa系数,因为方法1利用多源遥感数据选取景观格局指数,分析城市交错带功能与结构之间存在的关系,根据分析结果构建布局优化模型,实现城市交错带的布局优化,提高了总体精度和Kappa系数,获得了良好的布局效果。
将时间系数作为测试指标,采用方法1、方法2和方法3进行测试,时间系数越大,表明优化城市交错带布局所用的时间越长,相反,系数越小优化城市交错带布局所用的时间越短,图3为时间系数测试结果。
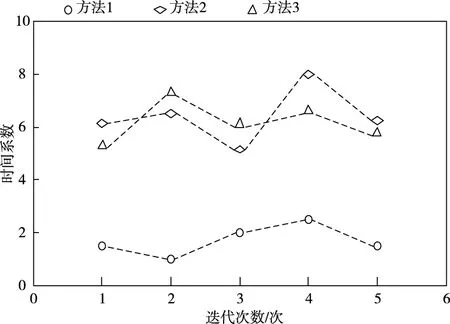
图3 不同方法的时间系数
由图3可知,方法1测试过程中获得的时间系数均低于方法2和方法3获得的时间系数,因为方法1利用计算的景观格局指数分析交错带空间结构,为城市交错带的布局优化提供相关信息,减少了优化所用的时间,提高了优化城市交错带布局的效率。
5 结束语
1)城市规模不断扩大,城市交错带的数量随之增加,对城市交错带的布局进行优化可以为土地管理、利用以及景观规划提供依据,由此,提出基于多源遥感数据的城市交错带约束布局优化方法。
2)根据获得的多源遥感数据选择和计算景观格局指数,提高了总体精度和Kappa系数的同时缩短了优化时间,精度最高可到94%,时间最高仅为2秒。
3)分析交错带空间结构,以及功能与结构之间的关系,解决城市交错带布局优化方法总体精度低、Kappa系数低和优化效率低的问题,为城市交错带的发展奠定了基础。
