虚拟手术缝合线实时打结仿真研究
2021-11-17张峰峰王荣淼
吴 昊,张峰峰,2*,詹 蔚,王荣淼
(1.苏州大学机电工程学院,江苏 苏州 215006;2.苏州大学苏州纳米科技协同创新中心,江苏 苏州 215123;3.苏州大学附属第一医院,江苏 苏州 215006)
1 引言
虚拟手术是虚拟现实技术在现代医学领域的一个典型应用,是一种可以替代传统医学培训方法并且具有巨大应用价值的新兴学科[1]。目前,虚拟手术的研究主要集中在软组织切割变形及缝合模拟,其中缝合线的打结作为手术缝合模拟中的关键环节也成为了一项重要研究内容[2]。手术缝合线作为一种柔性体,具有很强的抗拉伸变形能力并且能被随意弯曲、折叠。由于缝合线独特的形变特性,对于缝合线建模、动力学方程计算以及自碰撞检测算法等提出了更高的要求。
目前,针对虚拟手术缝合线等其它柔性体的仿真研究国内外已有众多研究成果,大致可以分成基于几何特征的仿真研究和基于物理特征的仿真研究[2]。Lenoir[4]等人使用基于样条曲线的几何仿真来模拟缝合线。根据能量方程,将缝线的变形最终转化为样条之间控制点的运动方程,并采用隐式欧拉积分法进行计算,但该方法不能很好的描述物理特性和反馈力。Joel Brown[5]等人提出了另一种几何仿真方法,用一系列的圆柱体通过首尾相连的方式表示线模型,利用FTL(Follow The Leader)算法,通过施加相应的物理约束保证线的特性。该方法的优点为简化大量计算,但是运动简单,稳定性较差。贾世宇[6]等人基于Joel Brown中的刚性杆模型和FTL(Follow The Leader)形变算法,并通过刚性杆结构和AABB层次包围结构实现绳子的自碰撞响应以及绳子与其它刚体之间的碰撞,并设置临时接触约束实现等效摩擦力,完成实时绳子打结仿真并带有力反馈;但是未考虑缝合线的物理特性,缺少动力学方程。Lang[7]提出了基于位置动力学(PBD)的Cosserat杆理论的手术线的实时仿真方法。该方法实现了手术线的稳定缠绕和打结,但是该算法基于物理模型,需要求解多个微分方程,计算量较大。梁民仓[9]等人对柔性绳索进行了研究,基于质点弹簧模型的结构弯曲弹簧模型,通过添加弯曲弹簧以限制绳子质点处的不正常弯曲现象,保证柔性绳索的稳定性和精度。王崴[10]等人提出了一种蜂窝状弹簧-质点模型应用于绳索形变仿真,质点间设置4种弹簧模拟绳索内部弯曲、扭转、拉伸等形变特性,采用非共线过滤器的剔除算法实现自碰撞检测,满足绳索模拟时的实时性、快速性,但模型结构过于复杂。
与上述文献[4]~[10]的研究相比,本文针对缝合线的物理特性,提出了MSS的物理建模方法并结合物体非线性及弯曲力学特性对其进行动力学解算。其次通过跟踪控制点实现了触觉设备对缝合线的运动控制,有效解决了缝合线运动仿真时效果失真等缺点。在传统的层次包围盒碰撞检测方法的基础上,提出了一种模拟受力方法实现缝合线打结过程中的自碰撞响应,增强了缝合线打结过程中的实时性和逼真度,最后完成了缝合线实时打结仿真。
2 缝合线模型描述
2.1 模型建立
根据手术缝合线特性,采用质点弹簧系统(MSS)建立缝合线物理模型,如图1所示。MSS方法是将缝合线离散成一系列有质量的粒子(质点),其位置信息为Pi(i=0,1,2…n)。质点间通过n个无质量的弹簧连接,设置质点的质量为m以及弹簧的初始长度为l0。缝合线的物理特性由其内部的质点弹簧模型决定,只需调整质点弹簧的物理参数就能得到不同性能的缝合线。缝合线的变形由质点运动产生,并受到连接弹簧的控制。

图1 缝合线模型
为了增加缝合线的光滑度,避免锯齿现象,将长为L、半径为r的一个完整的圆柱体作为缝合线的几何模型。将物理模型放置在圆柱体的几何中心线上,并构建模型表面网格顶点与内部质点间的映射关系,使得内部质点弹簧模型的形变效果转化为外表面几何模型的变形效果,实现缝合线的变形与打结的图像渲染效果[11]。
2.2 模型受力分析
手术缝合线为一种典型的形变线性体,其轴向长度比其它两个维度大得多。因此,缝合线在变形时表现出明显的非线性特性,其弯曲应变较大,且具有很强的抗拉伸能力。针对缝合线物理特性,需要对MSS模型进行合理的受力分析[12]。
在理想的弹簧模型中,根据霍克定律,弹簧拉伸力与弹簧的伸长量成正比。然而,现实中的缝合线具有很强的抗拉伸的特性,当变形加大时,其弹力会急剧增加,防止其形变过大。计算弹簧拉伸力需要综合考虑缝合线作为非线性物体的特性。缝合线的非线性拉伸力计算公式为

(1)
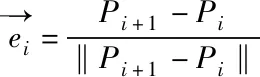
为防止弹簧发生过度形变,维护系统稳定,质点运动时应受到弹簧的阻碍。根据粘滞阻尼理论,弹簧阻尼力与相连质点速度有关,其公式如下
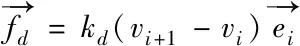
(2)
其中kd为弹簧阻尼系数,vi和vi+1分别为质点Pi和Pi+1的速度,可由式(8)求得。
缝合线模型中由于未能限制质点之间弹簧的弯曲度,造成线模型因受力发生弯曲或折叠形变过度,不能很好的模拟缝合线的几何效果。因此,模拟缝合线的弯曲特性是保证线模型平滑运动的基础。缝合线的弯曲特性是通过添加质点上的弯曲力来实现的。弯曲力是指柔性体由弯曲状态向伸直状态恢复时所产生的力。质点所受的弯曲力是由它前后两个质点间的弹簧弯曲程度决定,基本思想是:将两个连接的弹簧设置为三角形(两个弹簧不在同一直线上),假设弯曲力是将端点推到完全展开的位置。两个连接段的长度保持不变,只有垂直于弹簧线段的力分量才用于端点。如图2为弯曲弹簧模型。
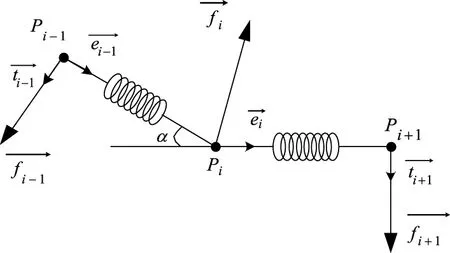
图2 弯曲弹簧模型
弯曲弹簧计算公式如下
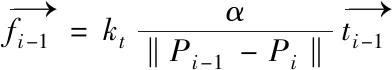
(3)
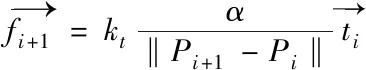
(4)
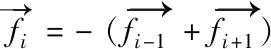
(5)

3 缝合线的运动模拟
3.1 运动模型求解
缝合线的质量质点受到内力和外力的共同作用,根据牛顿第二定律,其动力学方程可以表示为
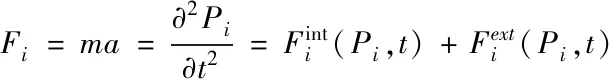
(6)

显式Euler法计算简单,但精度较低,系统运行不稳定。隐式Euler法在大步长仿真时系统稳定性较高,但计算量较大、速度慢,降低了系统仿真的实时性。Verlet法为居中计算,精度比基于前向计算的显式欧拉方法高,稳定性高,计算复杂度也较低。本文采用Verlet法对质点弹簧模型的动力学方程进行求解。针对式(6)使用verlet法求解质点位置和速度方程如下
(7)

(8)
其中Pi(t)、Fi(t)、vi(t)分别是在t时刻下质点的位置、所受的总力以及速度,Pi(t-Δt)为上一时刻质点的位置,Δt为时间步长。由上式可知,质点在t时刻下的位置Pi(t)和所受的总力Fi(t)及t-Δt时刻下的位置Pi(t-Δt),并根据间隔步长为Δt,可得到在t时刻的质点速度以及t+Δt时刻下质点位置。只要设置的时间步长Δt足够短,就能保持积分算法稳定,满足实时交互的需求。
3.2 基于控制点的运动轨迹追踪
基于MSS方法建立缝合线模型,由于缝合线形变较大、难以控制,会降低了线模型运动模拟的真实性,所以采用跟踪控制点的方法对线模型运动轨迹追踪。根据虚拟耦合技术[13]将触觉反馈设备的位置信息转化为缝合线上的任意质点的位置信息,该质点即为控制点。在每一个时间步长下,触觉工具对控制点施加外力,控制点进行位置更新。与此同时,求得与控制点相连的质点上的总力,并通过动力学方程计算该质点的位移与速度,即与控制点相连的质点发生位移变化,再由这些质点继续带动周围的质点移动。由此可知,任何一个质点都是依据与它相邻的质点的状态来计算的,缝合线模型为一个动态的形变模型。
图3显示了跟踪控制点的缝合线运动模拟。质点4为控制点,且在外力的作用下发生位移变化,进而引起与之相连的质点3和质点5发生位移变化,然后质点3和质点5又带动与之相连的其它质点运动,从而使线模型产生跟随控制点的平滑运动效果。

图3 跟踪控制点
4 缝合线的自碰撞检测与响应
缝合线的自碰撞是实现打结过程真实性和实时性的主要因素,也是打结仿真能否成功的关键。由于缝合线本身是一个细长的柔性体,没有太大的深度,并且随时间线模型形状不断发生变化。因此,快速精确地碰撞检测对缝合线打结模拟的逼真程度有着重要影响[14]。
根据缝合线分段式物理模型,使用传统的基于层次包围体结构(Bounding Volume Hierarchy,BVH)的动态碰撞检测算法,包围体为球体。根据缝合线物理模型形状自底而上构建层次包围球体树。每一个线段被一个最底层叶子包围球包围。相邻两个包围球形成一个父节点包围球,以此类推根节点为整个缝合线的包围球。缝合线的自碰撞检测算法是将层次包围球的自身与自身比较,根据自上而下搜索原则,搜索所有两个父节点包围球,如果两个父节点球体没有相交则一定不包含碰撞片段,不需要搜索其叶子球体。如果父节点球体相交则继续搜索其叶子球体。若叶子球体相交,需检测这两个球体中心的距离是否小于其半径之和,若球心距离小于半径之和表示发生碰撞。在缝合线模型上任意两个相邻的叶子球体都不发生碰撞。由于缝合线是可形变物体,层次包围球需要根据模型形状在每个时间步长下更新。
如图4所示PiPi+1和PjPj+1为缝合线任意两个不相邻的线段弹簧,缝合线碰撞检测是通过计算两线段包围球是否相交,即球心距离Oab(即为碰撞距离)是否小于包围球半径之和R=Ra+Rb。如果球心距离小于包围球半径,则认为线段弹簧发生碰撞。对于发生碰撞的两线段弹簧,碰撞响应处理算法应是将二者推开一定距离使其不再碰撞。本文采用一种模拟受力的方法,对弹簧两端质点添加排斥力避免缝合线模型发生穿透现象,该排斥力通过穿透深度法计算得出,其计算公式为
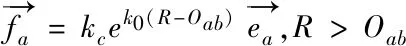
(9)


图4 线模型碰撞
5 缝合线打结仿真
仿真程序运行在惠普Z820工作站上。其配置为双Intel(R)Xeon(R)3.3GHz CPU。操作系统为Windows 7 Professional 。触觉反馈设备是瑞士Force Dimension公司制造的Omega 7.0。仿真程序是在 Microsoft Visual studio 2010平台下,使用标准C++编写,结合CHAI 3D中封装的OpenGL搭建缝合线仿真系统。

图5 系统仿真平台
基于物理模型的缝合线仿真中参数的选择尤为重要,模型的参数决定了整个仿真系统的稳定性以及效果的真实性。经过多次试验,确定了表1中缝合线的参数。
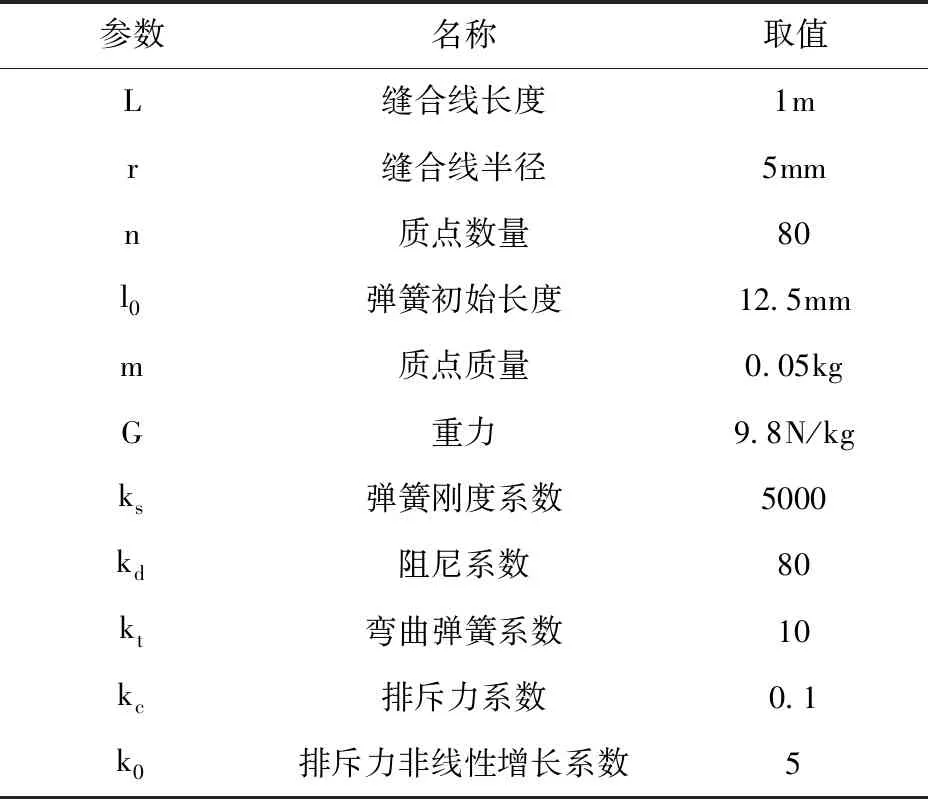
表1 缝合线参数设定
缝合线运动仿真如图6所示,图中的黑色小球代表触觉反馈设备的作用点,也是缝合线的运动控制点,用户通过触觉反馈设备拖动该控制点引导缝合线在虚拟空间运动和变形。图中可见通过跟踪控制点方法可以实现缝合线的运动控制,且缝合线的运动线条及大小拐弯处的表现非常自然流畅。
图6 缝合线运动控制
缝合线打结仿真如图7所示。由于只有一台触觉反馈设备,需将缝合线模型的一端固定,并利用触觉设备移动缝合线的另一端完成缝合线打结仿真。图7a为缝合线线运动初始状态。在每一个时间步长下,层次包围球算法将不断地对缝合线模型进行自碰撞检测。若检测到线段弹簧发生自碰撞,则在相关弹簧线段两端质点处强加排斥力,对线段间的运动产生“阻挠”,阻止缝合线穿透现象的发生,如图7b。图7c为缝合线的结处于松散状态。当用户通过触觉设备拉动缝合线的一端时,缝合线逐渐收紧,结以自然的方式结合得更紧,并随着距离的减小排斥力呈指数级增长,最终结将处于平衡状态,如图7d所示形成了一个紧密的结。

图7 缝合线打结过程

图8 排斥力
图8显示了缝合线模型在2000个时间步长内(包括一个打结操作和一系列线运动的过程)排斥力的变化过程。从图中可以看出,一些明显的峰值出现在靠近打结处的质点上,并随着打结完成排斥力将逐渐趋于0。在线运动的过程中,排斥力继续作用。
经上述实验可知,模拟缝合线模型内部非线性拉伸力、阻尼力以及添加弹簧弯曲特性,能有效地呈现出缝合线的形变特性,实现缝合线模型的平滑稳定运动。通过模拟受力的方法避免了缝合线自碰撞部分穿透现象的发生,这种模拟受力的方法不仅能够很好地实现缝合线的打结模拟,还能够实现力的交互,大大增加了虚拟仿真的沉浸感和真实性。在整个缝合线打结仿真过程中,图像刷新频率均满足30Hz以上的要求,该仿真过程实时性较好,图像反馈真实、流畅。
6 结束语
本文针对虚拟缝合手术中缝合线打结进行仿真。根据缝合线形变特性,在传统的MSS物理模型中引入了非线性拉伸、阻尼以及弯曲特性,避免了线模型形变过大且拐点不真实的现象。为了保证模型稳定性及精度要求,采用Verlet法求解动力学方程提高计算速度。通过跟踪控制点方法实现力反馈设备对缝合线的运动控制。基于传统的层次包围球碰撞检测算法,提出了一种模拟受力方法解决打结过程中缝合线模型自穿透问题。最后完成了缝合线的打结仿真并带有良好的触觉交互。通过仿真及实验,验证了本文算法的有效性,可以逼真地模拟缝合打结操作过程,且实时性较好,稳定性高。下一步考虑结合真实的手术缝合线打结,将缝合线与手术缝合针连接实现刚柔接触的动力学打结仿真。
