基于模式增长的嵌入式频繁子树挖掘算法研究

卫朝霞，邹倩影

(1.四川大学锦城学院，四川 成都 611731；2.电子科技大学成都学院，四川 成都 611731)

1 引言

频繁子树挖掘是数据挖掘的主要研究内容，在生物信息、Web结构分析等方面具有较高的应用价值。作为如此有价值的任务，同样也充满挑战，例如，即便使顶点集合缩小到最小范围内，仍然能形成很多结构不一致的树，并且每一棵树的不同节点能够取相同的权，这会导致对树的同构判断非常复杂。

针对上述问题，一些学者给出如下方法。文献[1]提出基于B-list的频繁子树挖掘算法。采用B-list数据结构挖掘频繁项集，将全序搜索树当作搜索空间，通过父等价剪枝方法限制搜索范围，并结合MFI-tree投影技术完成挖掘。实验结果表明，该算法无论在稠密数据集还是稀疏数据集中都有较好挖掘效果。文献[2]提出基于FP-Tree的频繁子树挖掘方法。将数据集合分为大小相同的模块进行挖掘，任意一个模块都运用三角矩阵的方式进行储存，并设计一个NCFP-Tree储存每个滑动窗口中的频繁项集，使用优化挖掘算法将每个窗口中频繁子树全部挖掘出来。该方法挖掘过程简便，挖掘准确率较高。

上述方法虽然简化了挖掘过程，但是不能描述数据对象之间的内在联系，在挖掘中会产生大量的冗余信息，影响挖掘效率。由于数据目标不仅是集合关系，更多时候是具有结构层次的，因此，在模式增长[3]的基础上对嵌入式频繁子树进行挖掘，并在挖掘过程中提出如下要求：数据库必须是大量且真实的；挖掘目标与知识需要满足用户要求，是可理解、可运用的，能够通过自然语言对其表达，并且带有特定约束条件。按照上述要求运用融合思想对数据进行清洗，获取融合后的压缩树，使挖掘结果中冗余信息量减少，进一步提高挖掘效率。

2 基于模式增长的嵌入式频繁子树挖掘算法

2.1 挖掘任务分析

在进行频繁子树挖掘之前，首先需要确定挖掘任务。指定树中全部节点的顺序，便得出有序树[4]。已知树T(v1)、标签集合L、顶点与边集合分别为N、B，标签树T(v1)存在映射f:N→L，则任意v∈N，f(v)=l∈L记为T(v1)=(L(N)，B)。

标签数据库属于标签树集合，其中，任意一颗树都是基于标签L的，若运用TDB代表标签数据库，则每个元组可以表示为(TID，Ti)。已知标签数据库TDB与模式树T，T的支持度表达式为

sup(T)=T(v1)|p(T)/X|

(1)

其中，p(T)为TDB所含T的实例数量，X为TDB中树的总量。若T的支持度sup(T)≥minsup(0≤minsup ≤1)，则T代表TDB中频繁子树，minsup 是用户规定的支持度阈值[5]。

2.2 模式增长性质与增长过程研究

2.2.1 模式增长性质分析

基于上述挖掘任务，通过模式增长方法对嵌入式频繁子树挖掘时会利用如下两个重要性质：

性质2：假设SD表示一个序列数据库，α为此数据库中某个ξ-模式，针对项目e而言，序列αe为SD中某个ξ-模式，则在α的候选后缀中，项目e属于频繁项。

可利用上述性质停止对频繁子树一条轨迹的搜索进程。假设β不是SD中一个75%-模式，则任意一个包含β的序列都不能成为75%-模式，同样不需要对以β开头的空间子树进行搜索。图1为所搜空间的裁剪示意图。

图1 所搜空间裁剪示意图

2.2.2 模式增长过程

在考虑模式增长性质的前提下将子树模式增长过程分为下述两步：

步骤一：对森林数据库D进行扫描，寻找全部频繁标识，每个标识均与一个长度为1的频繁子树相对。

步骤二：根据不同频繁1项子树，划分搜索空间。并针对任意一个频繁1项子树，建立与其对应的投影库，利用频繁增长点开拓已有子树模式，获得新模式。

假设U′表示一颗频繁k子树(k>1)，此时必然存在唯一一颗频繁k-1子树U，则U′是根据U的一个增长点获得的。

2.3 模式增长框架建立

采用最右路径拓展法[6]建立完整的模式增长空间，其本质为任意一棵频繁(k-1)-子树只能在最右路径的节点上进行增长，在此条件下构建一个新的频繁k-子树。

假设S(rs)表示频繁(k-1)-子树，w为树S(rs)的最后节点，则最右路径表示为

p=〈rs，u，…，w〉，u∈N

(2)

令函数pi代表返回路径中的第i个节点(i=0，…，|p|-1)，若T(r)为在p(i)中加入子节点后，根据S(rs)增长获得的频繁k-子树，当i=|p|-1时，称其为向下增长点；当0≤i<|p|-1时，p(i)属于向右增长点，增长数量表示为g=|p|。

针对某个待增长的频繁(k-1)-子树模式S(rs)，结合S(rs)拓扑结构，选取最右路径p，确定所有节点pi在数据库D中的投影，则全体投影组成S(rs)在pi处的投影库。此时，频繁子树挖掘转换为在S(rs)的增长点p(i)的投影库中挑选频繁节点的问题。若投影库中节点总数量为m，将所有节点加在p(i)上，组成p(i)的子节点。此过程能够通过递归进行[7]。模式增长框架示意图如图2所示。

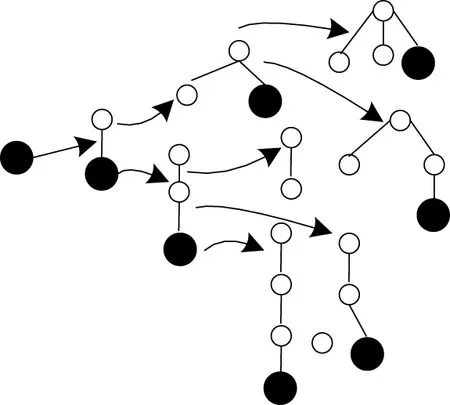
图2 模式增长框架图

图2中，粗线表示最右路径，阴影代表投影库。在增长模式下于数据库D中搜索由全部频繁节点组成的1-子树，将投影库中频繁节点添加到(k-1)-子树增长点中，即可生成多棵频繁k-子树。

2.4 基于融合压缩的数据清理

在实际应用中，造成数据不统一、丢失等现象的原因较多。例如收集设备出现故障、网络运行不平稳造成传输中断和输入错误等，由这些操作产生的数据通常会导致挖掘结果不可靠。因此，在做挖掘准备工作时，必须经过数据清洗去除数据不一致、丢失等现象，此外还要识别存在较大差异的数据，使其更加光滑，为挖掘工作提供质量更优的数据。数据量剧增会对挖掘工作造成影响，实际上并不需要对全部数据进行挖掘，通常只需要分析感兴趣的信息。因此，有必要对数据进行选择，筛选有相关特征要求的数据，避免在分析所有数据时占用大量挖掘时间，降低挖掘效率。

采用融合压缩树原理进行数据清理，融合压缩[8，9]的主要思想为：将森林数据库D做数据预处理工作，去除非频繁节点，获得处理后的数据库D′；遍历仅包括频繁节点数据库中所有嵌入式频繁子树Ti=〈Ni，Bi，Ri〉，找出与频繁子树Ti具有同样根节点的其它频繁子树Tj=〈Nj，Bj，Rj〉。假如根节点Ri的子节点不包括Rj的某子节点Ncj，此时需要建立一个包含Ncj信息的新节点，并将其加入到Ri的子节点Ncj中。进行嵌入式逐层遍历处理，将Ri每个子节点均进行清理。根据上述融合压缩思想，构建如下融合压缩树。

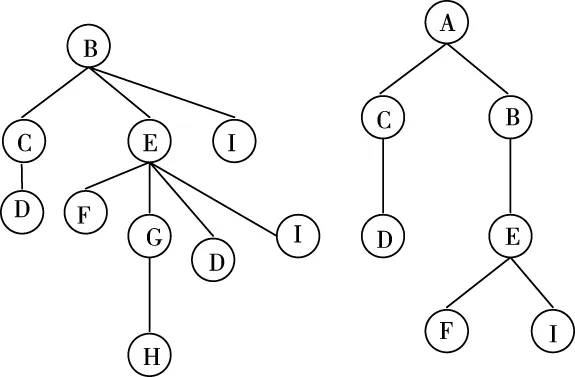
图3 融合压缩树示意图

2.5 树与森林的拓扑编码

基于数据清理结果，对树与森林进行拓扑编码，拓扑编码的方式有两类，一类是对投影库重新分配动态空间，该方法能够确保数据库中不会再有无用节点；另一种是使投影库和初始库共同享用同一个空间，采用过滤处理方法消除冗余节点。后者消耗内存较低，能够提升挖掘效率，本研究采用第二种方法参考数组结构的随机存取性质，确定树与森林的拓扑编码方式。

已知树T(r)，按照节点顺序排列可以组成一个标识符序列，并把描述节点层次的数据记录到序列中，使其包括树的拓扑信息，称其为树T(r)的拓扑序列。假如T(r)的最右节点是ω，则T(r)的拓扑序列表示为

top(T)=〈rlr，…ulu，…ωlω〉

(3)

其中，ulu为拓扑序列中的某个元组。

已知树T1(r1，N1，B1)与T2(r2，N2，B2)，若它们属于同质结构，则只存在唯一一个保序映射函数f:N1→N2，对于任意一个节点u∈N1，均有u=f(u)且lu=lI(u)

综上所述，树与森林的拓扑编码如下：

1)树的任意一节点分为三个域，分别是：lable(标识符)、level(层次)以及scope(等于)。

2)树是由节点构成的数组，节点在其中的位置和节点顺序需要始终一致。

3)森林是树组成的数组。

2.6 挖掘算法实现

结合数据清理结果与频繁子树拓扑编码结果，对嵌入式频繁子树实施挖掘，具体过程如下：

输入：森林数据库D与最小支持度阈值minsup 。

输出：频繁子树集Ω。

步骤一：扫描初始数据库中全部树的根节点，获取频繁1-子树集合L1，并将此集合中全部频繁1-子树加入到频繁子树队列freqtree-vec中。

步骤二：若队列freqtree-vec为空，返回到频繁子树集合Ω，反之进行下一步。

步骤三：根据覆盖定理对子树队列freqtree-vec做裁剪，去除被覆盖的频繁子树。

步骤四：从队列freqtree-vec中挑选一个元素，记为Fk，如果Fk不能拓展，则进行下一步操作；反之对Fk进行拓展，获得一个(k+1)-子树，并将其加入到队列freqtree-vec中，转至步骤二。

步骤五：把Fk加入到频繁子树集合Ω中，实现嵌入式频繁子树挖掘。

在实现频繁子树的挖掘后必须对时间复杂度进行分析。假设某个节点经过扩展后获得b个频繁子节点。此时，利用挖掘算法获取的最终频繁子树为一棵完全b叉树T。若此完全b叉树T的深度表示为d，节点总数是f，下述使用分治法分析时间复杂度。

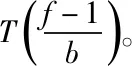
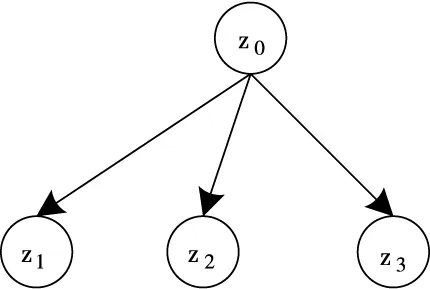
图4 时间复杂度分析图

因此，结合组合原理，可获得下述递推公式：

(4)

假设T(1)=1，则又存在如下递推方程：

(5)

由上述分析结果可知挖掘过程中产生的频繁子树数量是非常大的，属于指数级别。若在挖掘过程中对其进行裁剪，这样就可以降低算法的复杂度，若b等于2的机率是ρ，b为1的概率是1-ρ，此时时间复杂度计算公式为：

T(f)=ρ(2bd)=ρ(22dp×d(1-ρ))=ρ(22dp)

(6)

综上所述，通过数据清理与频繁子树队列裁剪，降低了挖掘过程的复杂度，实现对嵌入式频繁子树的高效挖掘。

3 仿真研究

为了验证基于模式增长的嵌入式频繁子树挖掘算法的有效性，通过仿真对比所提方法、文献[1]方法、文献[2]方法，给出不同方法的性能对比结果。实验数据集包括真实数据集CSLOGS和模拟数据集TreeGen，其中，真实数据集和模拟数据集中均包含两个分区，在上述两个数据集中挖掘频繁子树。实验均在一台ADM Athlon 3000+PC上进行，内存为1T，操作系统为RedHat Linuc 9.0，采用MATLAB软件进行数据处理。利用数据生成程序产生数据集合，其相关参数设置如下：树最大深度E=10，树最大扇初度F=6，在确保实验参数相同的情况下分别进行如下实验。

3.1 最小支持度相同

检测在最小支持度Smin=1%的情况下，数据集从10K～90K递增过程中不同方法挖掘频繁子树的总数量，实验结果如下图所示：

图5 最小支持度相同情况下频繁子树挖掘数量

分析图5可知，文献[1]方法与文献[2]方法挖掘的频繁子树总数量基本一致，但是所提方法的挖掘总数明显高于其它两种方法，主要因为该方法充分利用模式增长性质，逐层进行挖掘，从而得到更加全面的频繁子树。

3.2 数据规模相同

确定人工数据集为75K，最小支持度Smin从0.2%～1.8%逐渐递增，在此情况下，比较不同方法的挖掘总数。

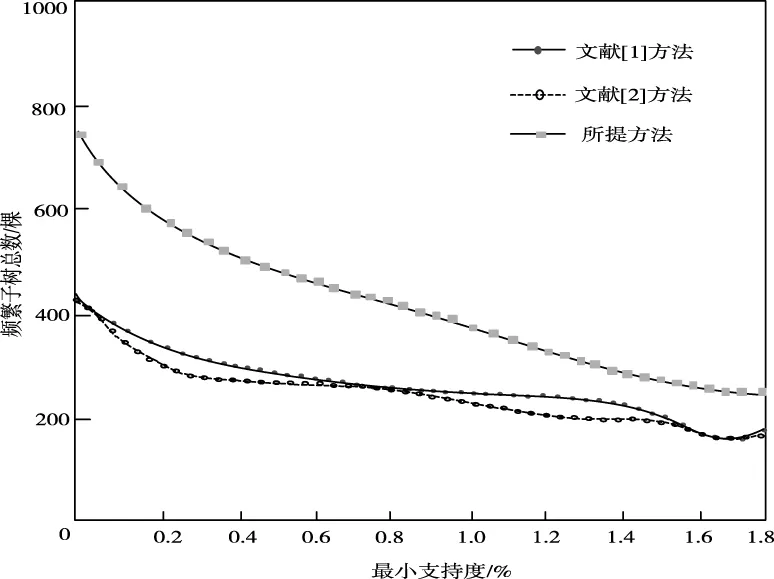
图6 数据规模相同下频繁子树挖掘数量

如上图6所示，在最小支持度逐渐递增的过程中，不同方法挖掘总数随最小支持度增加而减少。在相同支持度情况下，所提方法的频繁子树挖掘数量高于其它方法，特别是在支持度较小时，优势更加明显。这是因为其它两种方法都不包含隐含子树，而所提方法隐含子树出现概率较大，而隐含子树对挖掘总数量会产生较大影响。随最小支持度的增加，使频繁度提高，此时隐含子树出现概率降低，使频繁子树挖掘总量呈现下降趋势。

3.3 挖掘效率对比

使人工数据集从10K～90K递增，将最小支持度设置为Smin=1%，对比不同方法的执行时间。

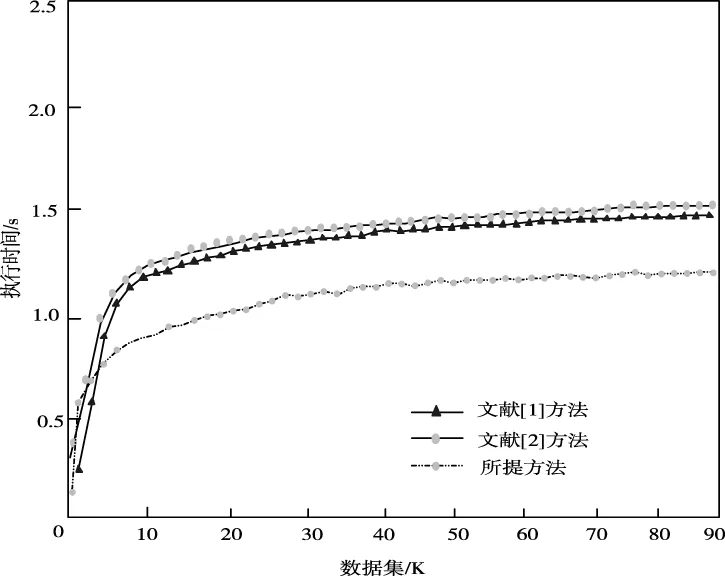
图7 不同方法挖掘效率对比图

图7中显示，当数据规模逐渐增大时，不同方法执行时间逐渐增加，但是所提方法执行时间总体上低于其它方法，其最高耗时约1.2s，主要因为所提方法对数据进行了清洗，并进行融合压缩处理，数据预处理不但能提升数据质量，还能获得更好的挖掘结果。减少冗余数据，提高了挖掘效率。

4 结论

为方便从海量数据中提取所需信息，利用模式增长方式对嵌入式频繁子树进行挖掘。仿真结果证明，所提方法在挖掘频繁子树较多的情况下，能够提高执行效率，并且与传统方法相比蕴含更多的结构信息。但挖掘模式还需进一步精简，在今后研究中，在一定的允许误差范围内，通过较为简便的挖掘模式即可满足用户挖掘需要，进一步提高信息分析工作的效率。