颗粒随机填充混合物介电性能仿真的新方法

2021-11-17钟汝能郑勤红

计算机仿真 2021年3期

钟汝能，郑勤红，，向泰，姚斌

(1.云南师范大学能源与环境科学学院，云南昆明，650500；2.云南省光电信息技术重点实验室，云南昆明，650500)

1 引言

在材料科学、电子电气和电磁工程领域，常常遇到大量基质颗粒随机分布于基体中的混合物质，如金属基复合材料、聚合物基复合材料、含有杂质的矿物质或自然堆放的粒状农产品等等，研究这类混合物的介电性能具有较好的价值[1]，然而，技术成本高一直是新材料研发或物料微波热加工器件设计中的瓶颈问题，建立有效的数值仿真模型先行进行性能预测已被广大研究者采用[2，3]。

众所周知，混合物的等效介电性能依赖于各组成成分的介电常数、比例、形状和位置分布等，且基质颗粒在基体中的分布都是非均匀体系，其形状、大小、位置的存在状态并非完全规则[4]。对此，学者们采用不同的技术方法开展了大量的模拟研究[5，6]，其中，Cheng采用ANSYS软件对颗粒无序填充两相复合材料的有效介电常数进行了数值模拟[7]；Rakesh等采用COMSOL多物理场仿真软件(COMSOL Multiphysics)模拟分析了金属核壳纳米/聚合物介质复合电容器的有效介电性能[8]；Zhao等采用蒙特卡罗法和有限元法模拟计算了立方晶格三维结构中双组分复合材料的复介电常数[4]；Jebbor使用有限元法和MATLAB软件仿真了二维情形下球形颗粒随机分布的复合材料介电性能[9]；浦毅杰基于蒙特卡罗方法，利用ANSYS的APDL参数化设计语言，构建了随机分布纳米颗粒增强陶瓷基复合材料性能数值分析模型[10]。前人的研究成果为工程的实际应用提供了借鉴，然而，在早期的研究中还面临着一些可以改进的问题：①大部分研究主要针对双组分混合物而开展，且在建立模型时或多或少假设了基质颗粒在基体中的分布是有序的重复单元，即颗粒的分布状态主要基于结构抽象化和颗粒规则化两种类型，颗粒的形状多以球体、立方体、椭球或层状等单一结构形状为主[11]，这些简化后的计算模型与混合体中颗粒的真实存在状态并非完全吻合；部分学者开展了颗粒无序分布对混合物性能的影响研究[12]，但研究内容侧重于颗粒的结构形状或者分布状态中的某一方面。②当前，针对多组分混合物和变温变频条件下混合物的介电性能模拟分析研究成果鲜见报道，在常用有限元商用软件中，COMSOL的多物理场耦合能力使变温变频条件下混合物的性能分析成为可能，然而，该软件中针对三维情形下颗粒随机生成及投放的功能缺失，需用户自行编制脚本程序来实现。

本文采用COMSOL的App开发器，编制了基于蒙托卡罗方法的颗粒随机生成和投放程序，构建了基质颗粒的空间位置、形状和体积在基体中随机分布的立方体多胞有限元模型，通过对数值结果的比较分析验证了方法的可行性和有效性，以期为混合物性能的深入模拟分析提供一种借鉴方法。

2 仿真原理和模型

2.1 颗粒填充混合物等效介电特性的仿真原理

当混合物中颗粒的尺寸远远小于电磁波波长时，可用准静态条件下的平行板电容器模型分析混合物的等效介电特性[6]。如图1所示，平行板电容器上、下极板的电势分别为φ1=1V、φ2=0V，侧面边界条件为∂φ/∂n=0，极板间为混合物。

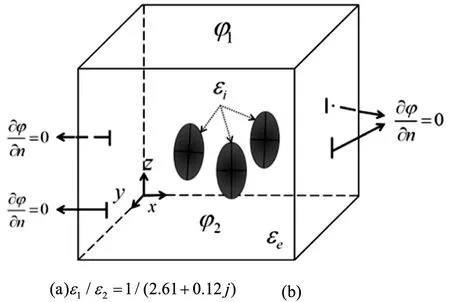
图1 颗粒填充双组分混合物模拟模型

在有限元方法中，每个网格单元所拥有的静电能为

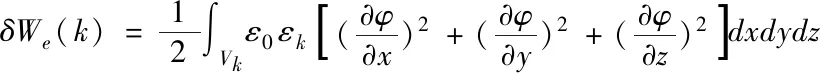
(1)

式中，εk和Vk分别表示第k个单元的介电特性和体积。混合体所诸存的静电能为

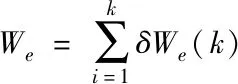
(2)

由电磁理论可知，图1所示电容器中所存储的静电能可等效地表示为[13]

(3)

式中，φ1-φ2为两个极板之间的电势差，d为两个极板之间的距离，S为极板的面积，ε0=8.85×10-12F/m，εeff为混合物等效介电特性。

令Wc=We，由式(2)、(3)即可获得图1所示电容器中混合物的等效介电特性(εeff)。

在分析微波频段下导电型混合物的介电特性时，物质的介电特性εk=1-j(σ/ωε0)，其中σ为电导率，ω为角频率(ω=2πF)，F为微波频率。

为准确模拟计算各向同性混合物的介电特性，可生成同一条件下的多个模拟模型，取其所有模型计算结果的平均值作为数值结果，即:

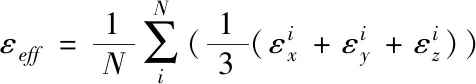
(4)

2.2 随机颗粒填充混合物的模型构建

2.2.1 模型构建思路

设定一个大的立方体(或长方体)代表基体，假设立方基体中可以划分出很多相似的小立方单元，每个单元由小立方基体和中心在立方对称中心附近、边界不超出单元边界的介质颗粒构成。与传统模型不同的是该单元不再是重复单元，即每个单元中颗粒的位置、大小和形状是随机分布的；对于同一个颗粒，它可能随机出现在所划分出的任意一个小立方单元中，颗粒的中心也没有固定在小立方对称中心，而是结合颗粒的结构参数随机分布在小立方对称中心附近。

2.2.2 颗粒生成及投放步骤

1)在COMSOL软件的“App开发器”中创建“Model method”，在“声明”中定义不同的数组、变量分别储存各颗粒的位置坐标值、体积值、体积比和结构参数。

2)将基体划分为M×N×P个相似的小单元，M、N、P根据混合物的基体结构进行设置，文中选取M=N=P=10。

3)根据实际需求，使用“录制”方法生成不同结构形状颗粒的建模代码备用，根据需要将代码嵌入到主程序中，设置结构参数变化范围，使用随机函数(Math.random)分步生成颗粒的随机位置坐标参数和随机结构参数。

4)将每组随机数与小立方单元中的填充颗粒建立对应关系，将随机值赋予拟生成颗粒，并通过程序判断语句，确保颗粒不溢出小单元、颗粒间可以接触但不重叠。

5)设定颗粒数量，编制程序将介电性能相同的颗粒设定为同一个“累积”，累积的数量根据混合物中颗粒的种类确定。

6)运行method方法，实现颗粒的随机生成及投放。

2.2.3 有限元模型构建和赋值

执行method程序，在指定区域生成立方体模型和颗粒模型，使用布尔运算将立方体区域减去颗粒区域即得到基体区域，形成“联合体”，完成模型构建。作为示例，图2显示了不同形状颗粒填充混合物的三维模型图，其中图2(A)为球状颗粒模型图，图2(B)为球状和立方状颗粒混合模型图，图2(C)为球状、立方状和椭球状颗粒混合模型模型图。

图2 不同形状颗粒填充混合物的三维模型图、颗粒网格剖分示意图

使用COMSOL网格剖分功能中的“物理场控制网格”对模型进行自由四面体网格剖分，并采用“中等”优化级别进行单元质量优化，图2(D)显示了图2(B)所示模型中颗粒网格的剖分情况。在材料属性中选取基体区域进行属性赋值，选择“累积”对不同的基质颗粒进行物理属性赋值。

可以看出，通过本程序可以实现任意不同结构形状的颗粒在不同体积分数下的随机化混合生成和投放，该模型更符合实际工程中基质颗粒物质在基体中的真实状态，且能实现多种组成成分混合物的模拟模型构建。

3 结果和讨论

3.1 随机模型的有效性

采用球状颗粒数值计算得到ε1/ε2为1/10时混合物等效介电常数εeff与体积分数fv的关系(见图3)，每个体积分数计算50个拓扑结构后取其平均值作为最终结果。将计算结果与Maxwell Garnet (MG)、Bruggeman、JayaSundere Smith (JS)等经典模型[14]进行比较，结果表明，体积分数计算范围fv∈(0，50%)的数值结果介于JS与Bruggeman之间，基质颗粒的体积分数较小时(fv<20%)四种模型结果比较接近，基质颗粒的体积分数较大时(fv>20%)数值计算结果介于JS模型和Bruggeman模型之间，但与MG模型相差较大。对于MG、Bruggeman和JS模型来说，MG主要适用于基质的体积分数相对较小时的球状颗粒情形，体积分数增大后会逐渐形成拓扑微结构，此时计算值会偏小；Bruggeman模型在计算两相无明显包围的对称有效介质时能获得较好的结果[15]；而JS模型考虑了混合物中各组成成分之间相互作用。所以数值计算结果在基质的体积分数较小时与3种经典模型吻合较好，而在体积分数较高时偏离MG模型，与Bruggeman模型和JS模型接近，这种变化趋势是正确的，说明所建立的随机模型是有效的。

图3 随机模型数值结果与经典理论对比情

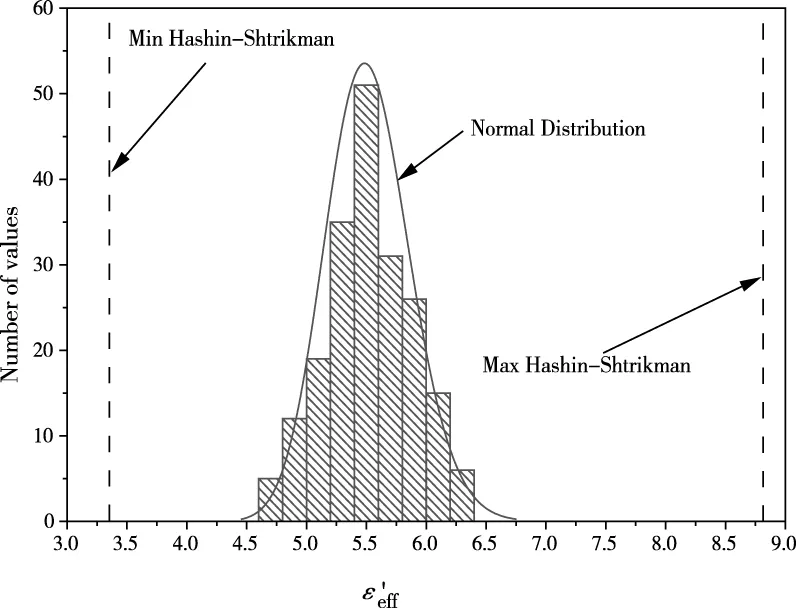
图4 随机模型数值结果的分布情况

3.2 数值方法的有效性

3.3 颗粒结构形状对混合物介电性能的影响

以聚偏氟乙烯双组分复合材料为对象(ε1=1、ε2=2.61+0.12j)，采用随机模型计算了颗粒为不同结构形状时混合体的等效介电常数，其中，A、B、C、D、E分别表示基质颗粒为球状、立方状、长方状、圆柱状和椭球状。图5(a)结果表明，当颗粒的体积分数较小时(fv<20%)，颗粒结构形状对等效介电特性的影响不明显；当颗粒的体积分数相对较大时(fv>20%)，等效介电常数大小与颗粒结构形状的对应关系为：εD>εA+B>εB>εA+C>εC>εA+D>εA>εD+E>εA+E>εE。分析可得，颗粒结构形状为D(圆柱状)和A+B(球状+立方状)时计算结果相对较大，此时数值结果与实测值[17]更加接近；颗粒结构为E(椭球状)时计算结果相对较小，这是由于椭球的特殊规则结构导致了粒子内偶极矩方向稍稍偏离[18]；其余结构形状对应的等效介电常数介于εD和εE之间。为便于比较，图5(b)显示了ε1/ε2=1/10时4种不同结构形状下εeff与fi对应关系，图示表明，当基质颗粒和基体的介电常数比相对较大时，上述趋势更加明显。

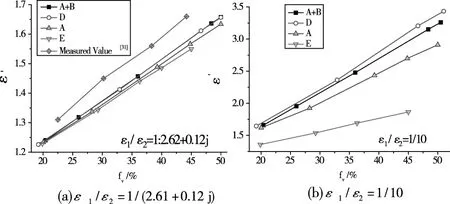
图5 颗粒结构形状对介电常数的影响

3.4 双组分混合物的等效介电性能分析

以聚偏氟乙烯双组分复合材料为对象(ε1=1、ε2=2.61+0.12j)，采用球状颗粒计算得到了混合体等效介电常数εeff与填充比fv的关系如图6所示，将数值结果与颗粒规则分布、位置随机分布和实测值[17]进行了对比。结果表明，由于随机模型考虑了颗粒的空间位置和体积的随机性，与颗粒为简立方分布、面心立方分布、位置随机分布时相比，数值结果更接近实测值，说明该随机模型具有更好的准确性。但精确地讲，无论是有序分布还是随机分布，计算结果比实测值都小一些，这可能与模拟颗粒的结构形状单一、颗粒的高阶多极矩贡献及多重散射效应引起的附加损耗有关[19]。

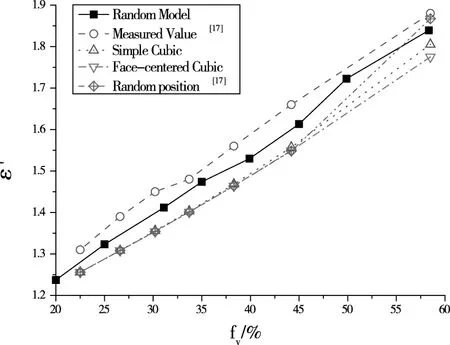
图6 采用随机模型计算的介电常数数值结果与文献值的比较(聚偏氟乙烯复合材料)

为评价随机模型在高介电常数比情况时的准确性，以BaTiO3/PVDF复合材料为对象(ε′BaTiO3=2000、ε′PVDF=9.6)，采用球状颗粒和立方颗粒计算得到体积分数为5%、10%、15%、20%时，得到复合材料等效介电常数分别为11.92、14.44、16.57、19.78，计算结果与实验值相吻合[20]。

3.5 多组分混合物的等效介电性能分析

以硅基氮化物陶瓷复合材料(SiO2-AIN-BN)为对象，使用随机模型计算三组分复合材料的等效介电常数，基体为SiO2(εSiO2=4.2-0.002j)，设定球状颗粒为第一基质相AIN(εAIN=8.8-0.076j)，立方状颗粒为第二基质相BN(εBN=5-0.040j)。选取各组分的体积分数比fSiO2:fAIN:fBN=7:1:2，得到SiO2-AIN-BN复合材料的等效介电常数为εeff=4.7286-0.0267j，计算结果与实测值[21]相吻合。