智能合约函数的建模与验证研究

叶昊榀，刘 阳

(南京财经大学信息工程学院，江苏 南京 210023)

1 引言

近年来区块链技术得到了快速的发展与推广。作为可编程金融的区块链2.0时代的代表技术[1]，智能合约在不远的未来将得到大量的推广与应用。智能合约无需可信中介、可以控制并处理大量的数字资产与交易，具有很高的经济价值。截至目前，市面上最为流行的智能合约应用平台以太坊的市值已经超过1800亿美元、完成了6.75亿次交易。智能合约极高的经济价值也吸引了大量的不法分子利用智能合约本身存在的漏洞实施非法攻击从而窃取数字资产。据相关研究表明，目前约有89%的智能合约都含有安全性漏洞，保守估计这些安全性漏洞所导致的损失已超过20亿美元[2]。为了给智能合约提供高层次的保障性，使用形式化方法对智能合约进行验证成为了许多学者的选择。Nicola Atzei等人[3]从Solidity语言、EVM和区块链三个层次对以太坊智能合约所存在的安全性隐患进行了总结。Joshua Ellul 和 Gordon Pace[4]展示了如何在智能合约领域中应用运行时验证的标准化技术。胡凯等人[5]提出了一种可以应用于智能合约生命周期的形式化验证框架和验证方法。Anastasia Mavridou[6]提出了用于智能合约形式化验证的VeriSolid框架、该框架同样支持对合约函数体进行建模。Anton Permenev等人[7]提出了VERX，能够证明以太坊智能合约的函数属性的自动验证器。Thomas Osterlanda等人[8]提出对Solidity语言的语义语法的形式化定义，并提出了一种将Solidity语言建模为PROMELA模型的转换方法。Zheng Yang等人[9]发展并证明了一种用于证明以太坊智能合约的可靠性与安全性的全新的形式化符号进程虚拟机。Giancarlo Bigi等人[10]通过将博弈论与形式化方法整合在一起的方式对智能合约进行了验证。Sukrit Kalra等人[11]提出了一个用于验证智能合约的安全性和公平性的框架——ZEUS。Tesnim Abdellatif等人[12]提出了一种全新的形式化建模方法以验证智能合约在其执行环境中的行为。Xiaomin BAI等人[13]介绍了形式化建模方法和形式化验证方法。

现有研究鲜有关注智能合约的函数性质的成果。本文通过将随机性引入到对合约函数的建模过程中，将函数建模为DTMC，实现了已有方法的改进，提供了对合约运行过程中可能产生的随机性现象的关注；同时本文通过添加标识符的方式提供了对break语句和continue语句的支持，实现了对以太坊智能合约所有控制语句的支持，进一步提升了算法的适用范围；通过对合约函数常用语句提供特定的处理方式提升了算法处理函数语句的能力。最终，本文的方法实现了更加普适地将智能合约的函数建模为DTMC并进行验证的目标。

2 建模智能合约函数

智能合约的实际功能是通过函数的触发和运行而得以实现的，因而智能合约在函数运行时的状态是值得研究的。同样的，一些恶意攻击者也会利用合约函数的漏洞破坏函数的原子性与隔离性，对合约状态产生影响、从中非法牟利。

本文希望通过使用随机模型检验的方式来建模合约函数并实现对函数的性质的验证，从而为智能合约的相关性质提供保障。

2.1 概览

为了实现以随机模型检验的方法建模并验证智能合约函数的函数体语句，本文将Mavridou A等人[6]的杰出工作进行了拓展，实现了将智能合约函数的函数体语句建模为DTMC，并为函数体语句提供了更加全面的支持。

2.2 智能合约与随机性

要将智能合约的函数建模为DTMC，需要解决两大问题：合约函数是否拥有状态和迁移？合约函数在运行时是否伴随随机性现象？

首先回答合约函数是否拥有状态与迁移。已有的相关研究[6]和Solidity官方文档均已表明合约函数是可以拥有状态与迁移的。

再回答合约函数在运行时是否会伴随随机性现象。以太坊智能合约在设计时被限定为确定性的、非随机的，其本身不会造成随机性现象。但合约函数在运行过程中会与环境产生交互，由于环境的不确定性，将会产生随机现象。例如，由于环境产生的参数不确定，合约函数在收到不同的参数时，可能会触发函数体内不同的语句块，从而造成函数运行结果的不同，最终造成函数输出状态的差异。因此，合约函数在运行时是伴随着随机性现象的。

基于此，认为智能合约的函数是可以被建模为DTMC的。

2.3 将合约函数建模为DTMC

2.3.1 智能合约函数简介

智能合约中声明函数的语法如下：

function functionName (datatype dataName)public payable modifierName()returns (dataType){ …}

若函数没有返回值，则“returns (dataType)”可以省略。函数名后紧跟的括号内为输入参数类型及参数名。modifierName()表示函数修饰器，其可以改变函数的行为。pubic为函数可见性，智能合约的函数可以分为public(external)和internal两种，前者不仅可以被其它合约调用，而internal函数仅可在本合约内部运行，即通过本合约的public函数调用而触发运行。

而require(condition)语句是目前最常用的条件判定语句，当condition表达式的值为false时，合约状态将自动回滚至该条require语句所在函数执行前的状态。基于该性质，require语句被大量的合约用于判定合约状态是否满足函数的触发条件。

2.3.2 迁移概率的假设

本文的研究是在已有的将智能合约函数的函数体语句建模为有限状态机的工作[6]上继续进行的，其将函数体语句的运行作为产生新状态的判定依据，通过对函数体语句进行分类，每执行一个特定的语句，便生成特定数量的状态和迁移。工作以此为基础，通过如下假设向迁移中加入了概率，以实现对随机性现象的考察。

假设一：在函数运行的某一状态中，其迁移概率是平均分布的。

对于合约函数而言，只有选择、循环等控制语句可能造成函数状态的分支；其余情况下，合约语句都是顺序执行的。因此，在对合约函数建模的过程中，如下图1所示，函数的大多数状态都只有一个后继状态，因而其迁移概率先天为1，满足设立的假设；对于由控制结构生成的状态迁移，如下图2所示，由于可能产生若干N个后继状态，因而其迁移概率为1/N，这样的假设固然十分简陋，却可以为研究提供很大的帮助，有能力验证合约函数的随机性质。而如何获得更加接近现实的概率则有待于进一步的研究。

图1 非控制语句对应产生的顺序状态迁移

图2 控制语句生成的分支结构状态迁移

2.3.3 对调用函数语句的简易支持

智能合约的函数同其它编程语言一样，智能合约函数也可以实现对其它函数的调用。本文将合约函数中调用了函数的语句分为两类处理：

1)调用的是public类型的函数，将其作为普通的顺序语句处理。因为可以对public函数单独建模验证处理，因此为了简化问题，这里不再将函数中调用的public函数展开建模；

2)调用了internal函数，对这类调用又可细分为两种情况：

a)对于诸如用于if(condition)中条件判定语句的调用，不进行展开；

b)其它情况则将进行展开处理，即对internal函数的语句进行建模；

通过这样的处理，文中的方法实现了对合约函数中调用函数语句将的简易支持。

2.3.4 控制语句的全面支持

智能合约Solidity语言的控制结构共有if、else、while、do、for、break、continue、return等8种，Mavridou A[6]的工作未提供对do、break、continue语句的支持。文中的工作提供了对这三种控制结构的支持，从而实现了对合约语言控制结构的全面支持。

其中在处理do语句时，借鉴了文献[6]对while语句的处理方法，这里不做赘述。

continue语句用于跳过本次循环体中余下尚未执行的语句，立即进行下一次的循环条件判定；break语句用于在循环结构中结束本层循环体。设立了一个标识符loop以确定函数执行break或是continue语句时合约处于第几层循环。在建模开始时，loop=0，其后随着算法的运行、建模过程的推进，每进入一层循环，置loop=loop+1；同样的，没处理完一层循环体的语句，便置loop=loop -1。通过这样一个简单的方式，可以明晰所处理的语句位于哪一层循环体，从而实现算法可以正确的建立对应状态的迁移、实现了对break语句和continue语句的支持。

2.3.5 require语句的处理

如前所述，大量智能合约的函数使用require语句以判定合约状态是否可以触发合约函数。对此本文将require语句作为一种特殊的语句进行了处理的细化。

对于require(conditon)语句，若conditon语句为真，则合约函数将运行下一语句；否则将回滚至合约函数运行之前的状态。因此将对require语句进行了如下处理：

如下图3，设函数的初始状态为Sinit，当前状态为Sin，当条件不满足时，状态回滚，则增加迁移Sin→Sinit，并记迁移概率为Prevert；当条件满足时，新增状态S′，增加迁移Sin→S′，迁移概率为1-Prevert。本文中，在概率平均分布的假设之下，有Prevert=1-Prevert=0.5。

图3 require语句建模效果图

2.3.6 建模流程简介

在介绍完本文所做工作后，介绍一下使用本文算法对合约函数的函数体语句建模流程。由于本文的工作是直接对合约函数建模，因而使用本文方法对函数建模的流程与原研究有所不同。具体的建模步骤总结如下：

1)按顺序将合约函数的修饰器语句加入到合约函数的函数体之中；

2)确定触发、输出状态并调用算法：若函数不包含require语句或函数未改变其require中条件语句包含的变量值，则新增状态S0，以p=1，loop=0调用算法functionAugment(S0，S0，S0，1，stmts)；否则新增状态S0，S1，以p=1，loop=0调用算法functionAugment(S0，S0，S1，1，stmts)，其中stmts为函数体语句。

该算法将函数体语句分为12类，每类对应相应的转换方式。这里限于篇幅将仅展示算法中的部分类别语句，完整的算法可以通过复制并访问https:∥pan.baidu.com/s/11nQRSezd6ajQdJrcsztQDA，提取码67p9获得。

算法X.functionAugment(SINIT，SIN，SOUT，pIN，stmt)

1)if loop=0:

2)functionAugment(SINIT，SIN，SOUT，PIN，stmt，SIN，SOUT);

3): functionAugment(SINIT，SIN，SOUT，PIN，stmt，SIN，SOUT，S[loop]loopInit，S[loop]loopEnd);

算法X.functionAugment(SINIT，SIN，SOUT，PIN，stmt，SLOOPINIT，SLOOPEND)

1)if stmt is a require(condition)statement:{

2)add a transition SIN→ SINITwith probability P=PIN*(1-Prevert);

3)add a transition SIN→ SOUTwith probability P=PIN*Prevert;}

4)else if stmt is variable declaration statement ‖ event statement ‖expression statement:{…

3 实验结果与分析

为验证本文的提出的建模方法，首先将本文的算法应用于部分智能合约的合约函数之中。囿于篇幅，这里只选取下节将用来验证性质的3个函数进行建模展示。

3.1 建模结果与分析

Mavridou A等人根据Solidity官方合约改编的blindAuction合约的withdraw函数与undid函数的代码如下图4、图5所示，其生成DTMC的状态迁移图则如图6、图7所示。

需注意的是withdraw函数生成的DTMC中的三处迁移：S7→S8和S6→S8与unbid函数生成的DTMC中的S5→S6。这三处迁移对应的是函数体中的transfer语句。正如Mavridou A等人在研究中的表述[6]，仅从生成的DTMC看，文献的方法可以避免在执行transfer等语句后对fallback函数的调用从而消除了“可重入性脆弱”。

图4 文献[6]中合约withdraw函数代码

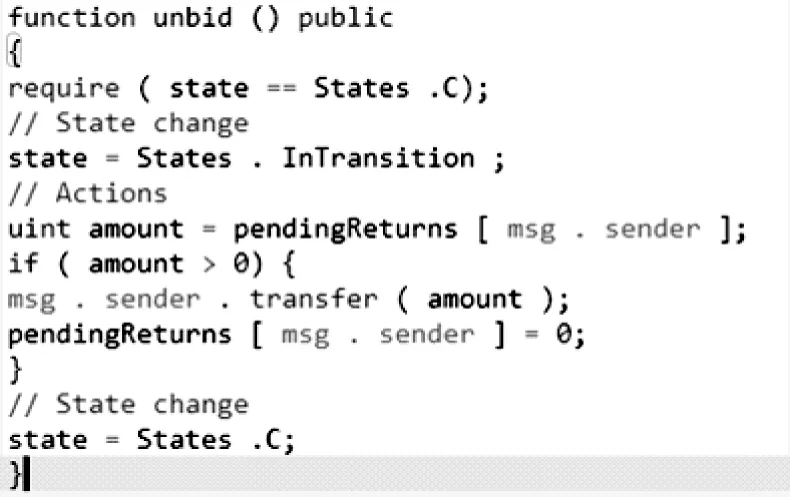
图5 文献[6]中合约unbid函数代码

图6 withdraw函数所生成DTMC

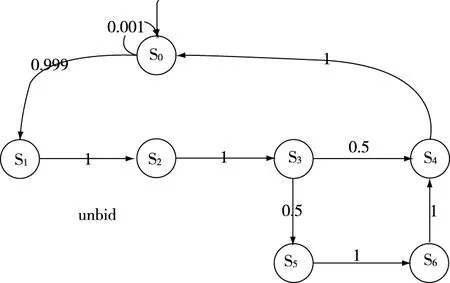
图7 unbid函数所生成的DTMC

Solidity文档中的blindAuction合约的withdraw函数的函数体语句代码及函数体生成的DTMC分别如下图8与图9所示。由于这里的DTMC状态相对较少，因此就很难看出是否存在“可重入性脆弱”。

图8 blindAucion合约withdraw函数代码

图9 withdraw函数所生成的DTMC

3.2 验证生成的DTMC

对于智能合约函数而言，最易遭受的攻击就是利用“可重入性”漏洞破坏函数原子性进行的，对此，本文规约了一条PCTL公式以用于验证智能合约遭受利用“可重入性”漏洞的攻击时是否安全：

对于智能合约而言，到达状态r后，系统在到达状态j之前不会到达状态i：

(s=r)i，P-≤p.[(!(s=j))U(s=i)]

(1)

本文对此前生成的DTMC的最终得到验证结果如下表1所示。正如上一节所做的分析，文献[6]中的两个函数不存在可重入性漏洞，而Solidity文档示例合约的函数也通过了验证。由于对以上合约函数进行可重入性漏洞的安全性验证均得到了通过，为了验证方法的正确性，对Atzei N等人[3]提出的存在可重入性漏洞的实例合约SimpleDao进行了建模验证，其未通过验证。该结果有力的证明了本文方法的正确性。

表1 函数“没有可重入性漏洞”验证结果

4 结束语

本文基于已有研究，通过增加对随机性的关注和合约控制语句的全覆盖，提出了一种将智能合约的函数建模DTMC的方法。本方法首先通过向状态迁移过程添加概率的方式实现了对随机性现象的关注；其次，通过对函数类型的分类，提供了对函数调用语句的简易支持；第三，增加了对break语句和continue语句的支持，实现了对智能合约所有控制语句的支持；最后，细化了前人研究的部分细节，对部分语句提供了差异化的处理方式，改进了算法的处理效果。最终的实验结果表明，本文的方法可以实现将智能合约函数的函数体语句建模为DTMC、实现对智能合约全控制语句的支持等目标。同时，本文对由智能合约所生成DTMC的性质规约与验证的结果也表明了本文方法的正确性。