短时延多包传输网络容错控制数学建模仿真

柴沙沙

(四川大学锦城学院，四川 成都 611731)

1 引言

传输网络控制方法可以通过加入实时通讯网络而形成一种分布式的闭环控制，将该系统应用到网络传输过程中，可以在一定程度上加快数据传输的效率。然而在传输网络的影响下，传输的数据会出现丢包、时延、时序错乱等现象，甚至会降低网络的稳定性，同时受到传输网络结构和带宽的限制，使得网络中的硬件设备无法正常使用，因此，采用多包传输的方式具有更加实际的意义[1]。多包传输是指传感器或者控制器的数据被放在多个不同的网络数据包中，在控制对象不同步的情况下，数据包极易出现时序错乱的问题。并且在网络诱导时延的情况下，网络时延可以分为常数时延和随机时延两种形式[2]。为了解决短时延多包传输网络中存在的时延、丢包以及时序错乱等问题，需要采用对应的容错控制方法实现网络控制。一般来讲，当传感器、执行器或其它元部件发生故障时，导致网络传输数据出现时延或丢包等情况，利用控制系统保证闭环系统的稳定运行。

容错控制可以从多个角度进行分类，按照克服故障部件分为传感器、执行器和控制器容错；按照设计方法可以分为主动容错控制和被动容错控制[3]。现阶段网络容错控制方法有基于神经网络控制、基于反推方法的自适应网络控制以及粒子群优化计算的网络容错控制方法。基于神经网络控制方法的实现主要依靠神经网络改进算法，逐层分析网络中的每一个节点，并对节点进行故障分析和判断，针对存在故障的节点进行容错控制处理，然而在网络传输运行的过程当中，网络中的所有节点均处于动态的状态，因此使用该方法的响应时间较长[4]。自适应控制方法解决了神经网络方法中存在的动态性问题，针对每一个节点分别进行检测和控制，这种方法在使用过程中响应时间较长，控制效率较低。粒子群优化计算控制方法的实现主要利用粒子群算法，这种算法在网络传输运行的过程中，响应时间较长，也就导致了控制效率较低。

针对传统方法中存在的普遍问题，提出网络容错控制的数学建模方法，建立对应的数学模型，将不同的网络故障状态进行分类，针对不同的故障分布采用不同的控制方法，以此来提高网络容错控制的效果。

2 网络容错控制数学模型设计

2.1 模型原理

短时延多包传输网络容错控制数学模型建立与设计的主体思想，是对执行多包传输任务的网络进行异常检测，从而判断网络的运行状态和故障类型，针对不同的故障类型，使用不同的容错控制方法来实现容错控制。网络容错控制数学模型的基本控制结构如图1所示。

图1 网络容错控制模型结构图

根据图1的模型结构，对网络容错控制数学模型进行搭建，其中以连续的多包传输数据作为被控对象，模型中的控制器为主动容错器。网络传输过程中各个节点的工作方式可以分为时间驱动和空间驱动两种方式，一般传感器节点为时间驱动，执行器节点为空间驱动，在容错控制数学模型中，对不同的故障类型进行具体分析与控制。

2.2 网络状态割点检测

执行多包传输的网络一般处于两种状态，一种为正常运行传输状态，另一种为异常状态[5-6]。引起异常状态的原因不同，主要分为网络线路问题和节点故障问题。其中网络线路会引起数据丢包和时序错乱，而节点故障问题会导致传输时延，甚至传输失败[7]。在建立网络容错控制数学模型前，首先需要检测网络线路与节点的状态。将被控对象的状态用式(1)来表示。

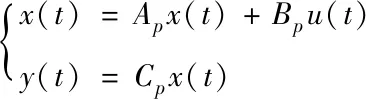
(1)

式中，Ap、Bp和Cp均为相应的空间维数，x(t)、u(t)和y(t)分别为被控对象的状态、输入和输出。假设短时延网络容错控制的离散状态表达式为：

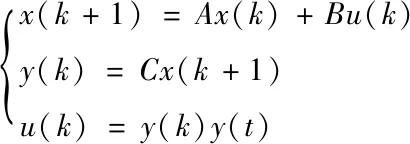
(2)

式中，x(k)为状态向量，u(k)为执行器输出状态，y(k)为传感器的输出状态，且式(2)中的A、B、C均为节点参数。

采用割点检测方法对被控网络的对象进行检测，割点检测方法的执行流程如图2所示。

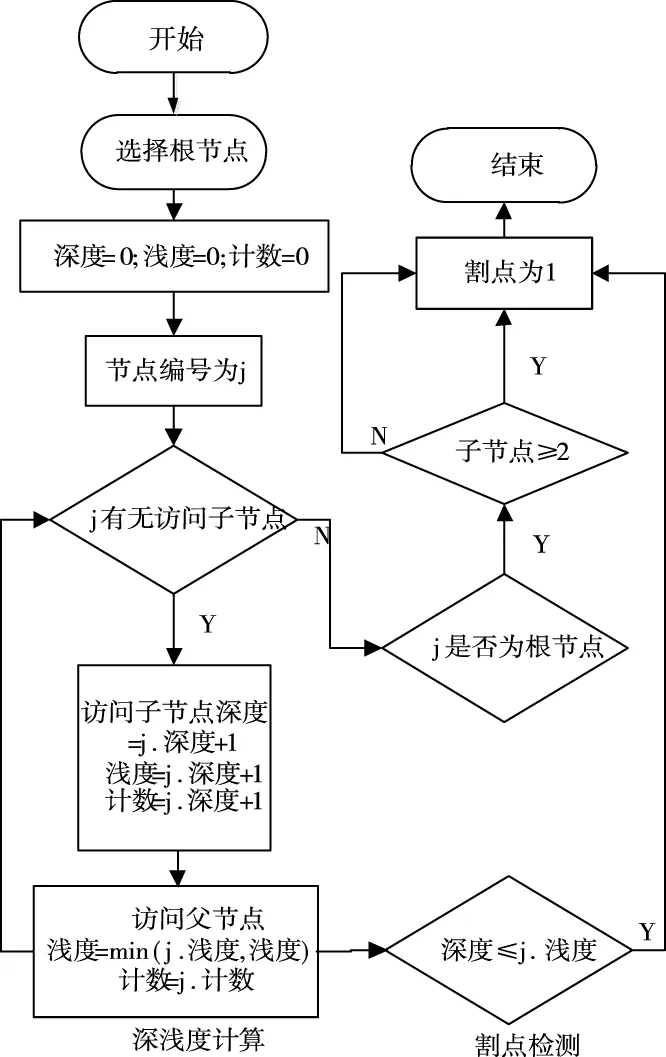
图2 网络状态割点检测流程图

按照图2中的网络状态割点检测流程，首先在被控网络对象中确定一个根节点，以根节点为起点，向其相邻的节点传输检测消息，直至遍历网络中的所有节点为止。检测消息在网络中以深度优先的顺序向节点进行访问，同时在节点中更新深浅度参数[8]。以深浅度参数的更新结果作为参考，判断数的节点是否为切割点。若节点i的子节点不小于2时，则判断i为切割点，否则进行下一步检测传输。由此便将网络中的多个节点划分成为多段，每段上的节点状态相同，因此，只需对一段线路中的某一个节点进行状态判定，便可以得出该条线路上所有节点的状态，说明该方法能够简化状态检测流程[9]。再将存在异常状态的节点进行具体划分，并按照卡顿故障、偏差故障、失效故障和丢包故障对节点进行分组输出。

2.3 容错故障分类

为明确建模所适用的范围，根据网络状态的测试结果，分别对不同故障问题进行问题描述。

高校突发事件的发生，往往是因为多方面因素影响的结果，因此在预防高校突发事件发生上面应当建立完善的预防机制，从而降低突发事件发生概率。同时在发生突发事件后也能够及时进行处理，将突发事件带来的影响降到最低。

对传感器和执行器失效造成的丢包故障问题进行描述，其描述的表达式为

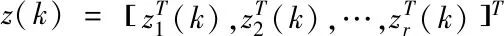
(3)

式中，z(k)表示多包传输网络可能出现的所有故障类型；T表示故障持续时间。在容错故障分类过程中需要考虑传感器节点的具体传输情况。在考虑输出时延时，则传感器节点的时延输出w(k)可以表示为

w(k)=δiCu(k)+(Ii-δi)z(k)

(4)

式中，δi表示节点布置，取值为diag(0，…，Ii)；Ii表示传感器信号被更新后的输出结果。如果第i个传感器在多包网络传输过程中发生数据包丢失故障，控制器将无法获取数据包丢失部分的数据信息，则可以判定传感器节点暂时失效[10]。

网络卡顿故障是执行器在运行过程中由于某些原因，导致传输的数据停留在某一个环节，且停留的时间超过正常传输的时间。将网络卡顿故障用式(5)表示

i=1，2，…，m

(5)

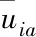
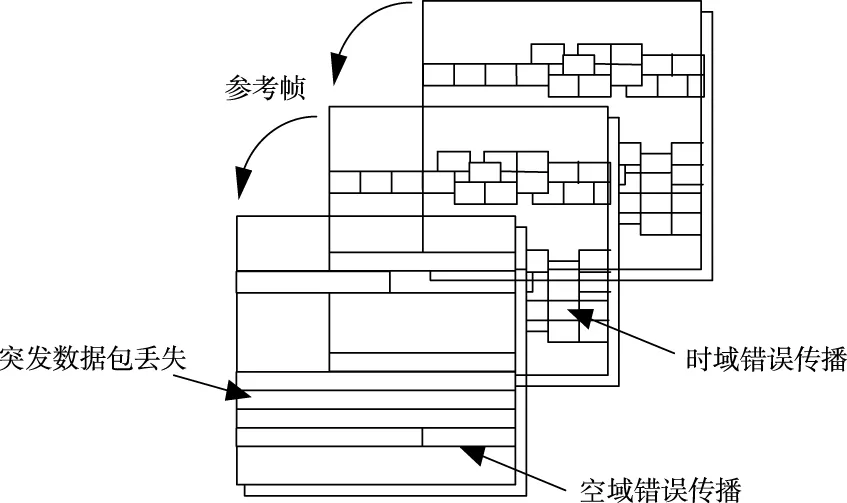
图3 时域空域错乱偏差故障示意图

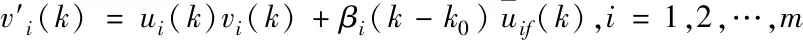
(6)

根据几种故障类型，使用不同的容错控制方案，针对多包传输网络，数据包在静态调度和动态调度情况下，设计网络容错控制器。

2.4 容错协同控制器设计

假设主动容错控制器极点为时间驱动，其工作周期为h，且主动容错控制器与控制对象的时钟完全同步。主动容错控制器中各个节点的时序情况如图4所示。

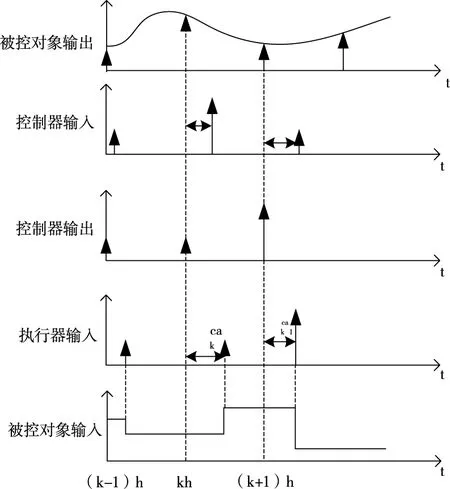
图4 主动容错控制器的时序控制图

设主动容错控制器表示为

(7)

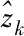
2.5 运用数学迭代算法实现容错补偿控制

如果网络中不存在时延、故障和干扰等不确定性因素，即fa(x，u，r)和e(k)的取值均为零，将此网络模型Am作为参考模型，并加入参考输入e(k)，可以通过节点配置的方法确定反馈增益变化，保证主动容错控制器稳定。网络在控制器的作用下，与参考模型相加得到误差动态方程

e(k+1)=Ame(k)+f(x，u，r)

(8)

式中，e(k+1)=x(k)-xm(k)，表示网络状态的跟踪误差。根据式(8)可以看出，若式中的参量f(x，u，r)的值为零，则误差也衰减到0，执行多包传输任务的网络即为稳定；若f(x，u，r)的取值不为零，网络就不够稳定，需要利用设计完成的主动容错控制器计算补偿控制量d(k)，其计算方法如式(9)所示

d(k)=uke(k+1)+dc(k)

(9)

式中，dc(k)表示克服时延、故障、干扰组成的非线性函数，从而保证网络的稳定性能。根据误差表达式，设计数学迭代学习容错控制补偿模型dk+1(k)，其表达式为

dk+1(k)=dc(k)+K1d(k)+K2e(k+1)

(10)

式中，K1和K2分别表示的是待定时延补偿和增益变化。依照数学迭代算子，可以计算出多包传输网络数学迭代容错补偿控制模型δfk(t)，其表达式为

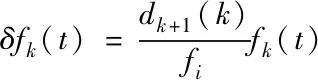
(11)

式中，fk(t)表示容错补偿控制量；fi表示故障增益。利用设计完成的控制器，实现短时延的补偿。分别针对不同的故障，使用数学算法实现网络的容错控制。分别从丢包、失效和时序错乱三个方面实现网络的容错控制。其中，当执行器或传感器完全失效时，fi的值为零；执行器或传感器完全正常时，fi取值为1；当执行器或传感器发生部分失效时，fi的取值介于零和一之间。那么当网络节点出现故障时，短时延多包传输网络容错控制数学模型在主动控制器的作用下，会使闭环网络趋于稳定状态。

3 仿真分析

为了检测短时延多包传输网络容错控制模型的有效性，需要设计仿真，对多包传输网络容错控制的结果进行分析。为了保证仿真变量的唯一性，在实验过程中选用相同的传输网络，并传输相同的多包数据。通过搭建容错控制模型应用的实验环境，对执行多包数据传输任务网络上的各个节点进行容错控制，并对网络控制结果进行具体分析。

3.1 仿真对象

对正在执行多包数据传输任务的网络进行采样处理，传感器和执行器节点的采样时间为0.05秒。在仿真环境下，手动设置网络的故障情况，对执行器故障情况进行仿真。根据故障模型使用开关阵列来表示执行器的故障模式，设置仿真对象的故障模式为连续时序错乱，设置的错乱跳变情况如图5所示。

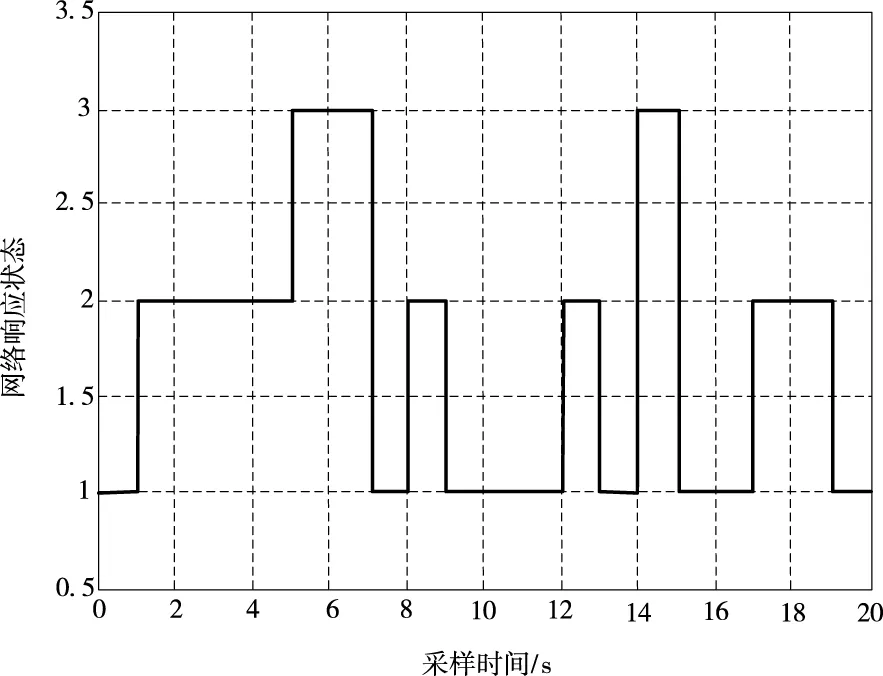
图5 仿真对象网络连续错序跳变曲线

在该网络故障下，使用设计出的短时延多包传输网络容错控制模型对故障的网络进行容错控制。

3.2 仿真过程

为了凸显设计出的多包传输网络容错控制模型的控制性能，在仿真中设立传统的基于反推方法的自适应网络容错控制方法和粒子群优化计算的网络容错控制方法作为实验的对比方法。在相同的仿真环境下，分别将三种容错控制模型应用相同的实验对象上。设立网络中的普通节点、执行器节点以及传感器节点作为仿真的检测对象。启动网络传输任务，并间隔5分钟启动一次网络故障，通过仿真过程，对比本文容错控制数学模型和传统容错控制模型的响应时间以及控制结果，进而得出不同模型的控制效果。

3.3 实验结果与分析

经过仿真过程，得出有关于网络容错节点控制的响应状态结果，如图6所示。

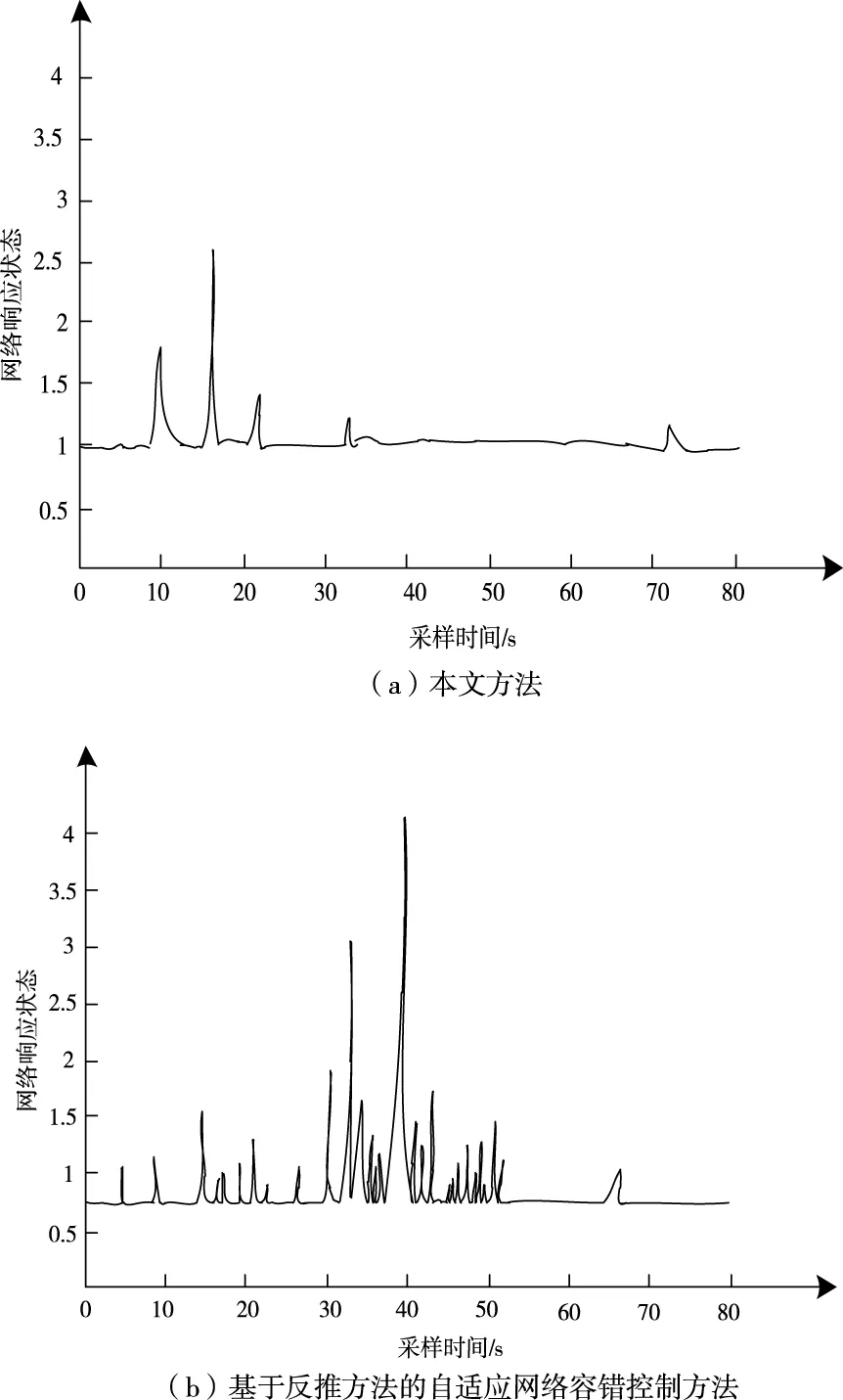
图6 响应状态对比结果

根据图6中曲线的变化形式表明，随着网络采样时间的增加，不同容错控制方法均起到的一定的作用，其中设计的容错控制数学模型在采样时间为22秒时，网络中的各个节点就已恢复到正常运行的状态，而基于反推方法的自适应网络容错控制方法需要花费约50秒的时间，粒子群优化计算的网络容错控制方法需要花费约65秒的时间。相比之下，本文容错控制数学模型大大缩短了响应时间。这是由于本文设计了主动容错控制器，利用控制器计算不同故障类型下的补偿控制量，并通过数学迭代算法实现容错补偿控制，从而获得了更加准确的网络容错节点控制的响应状态结果。

为了进一步验证本文模型的有效性，对本文容错控制数学模型和传统基于反推方法的自适应网络容错控制方法、粒子群优化计算的网络容错控制方法进行对比分析，对比结果如图7所示。

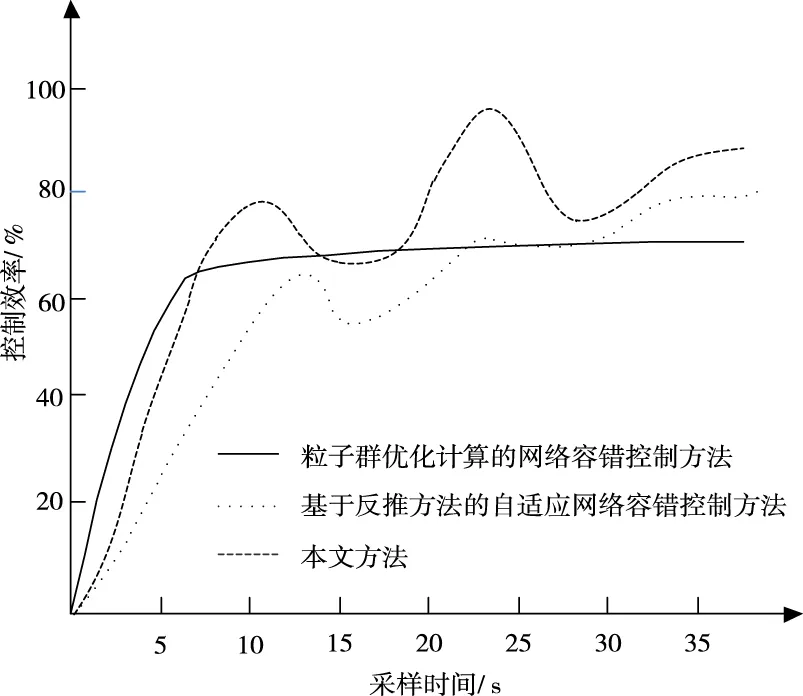
图7 控制效率对比结果

根据图7可知，本文容错控制数学模型的控制效率最高约为97%，而基于反推方法的自适应网络容错控制方法的控制效率最高约为78%，粒子群优化计算的网络容错控制方法的控制效率最高约为68%，本文方法明显高于两种传统方法。这是由于该方法采用割点检测方法对被控网络的对象进行检测，有效降低了检测过程的复杂度，进而缩短了响应状态达到正常运行状态的时间，提高了模型的响应效果。

4 结束语

考虑短时延多包传输网络在数据丢包和时延同时存在的情况，建立短时延多包传输网络容错控制数学模型。通过仿真表明，将该模型应用到网络当中，可以全面的控制网络中的每一个节点，验证了所给出的容错控制模型具有较高的控制效率，且在控制过程中的响应时间较短。虽然本文方法取得了一定的研究成果，但是由于用户对网络需求的日益增长，需要对该方法进行进一步优化，以此来满足实际需求。