视觉传达下多聚焦图像相邻像素图层融合仿真

赵 擂

(河南理工大学，河南 焦作 454003)

1 引言

多聚焦图像融合作为图像融合的一个重要分支，已经广泛的应用在目标识别、数码相机和机器视觉等领域。但实际应用中，大多数光学镜头无法使同一场景多个目标都在同一聚焦区域，这种情况就导致图像出现模糊。因此如何对多聚焦图像中相邻像素图层进行有效融合，使结果更为清晰成为现阶段的关键研究课题。

针对上述问题，国内外学者进行了一系列研究，提出以下几种解决方案。文献[1]首先根据图层和三角网模型拓扑结构，估计子图层的特征差异，选择不同参数与约束条件并分层提取图层几何、图层语义数据，构造两种类型不同的图层，最后通过缓冲区方法对提取出的语义数据和几何信息完成融合。但该方法在选择图层参数的过程中，需要反复试验参数的比值，存在时间开销大。文献[2]提出了一种基于多尺度分解和显著性区域提取的多聚焦图像图层融合算法，首先使用边缘保持下图像平滑算法，建造一个多尺度图像分解框架，把图像分割为不同大小的基础层图像和若干细节层图像，同时引入导向滤波器，对所有分解图层进行显著性区域提取。最后通过加权重建进行信息融合，从而达到任务目的。但该方法的过程较为繁琐，导致融合图层的过程较为缓慢。文献[3]提出一种基于小波变换的图层融合算法。首先将图像进行分割，使用小波多变特性保持相邻像素间的空间信息，再使用小波图层融合算法融合其图层。上述方法中存在一定弊端，因多聚焦图像在分割时，很容易受到外界影响，导致分割不准确，从而使图层在进行融合时出现融合不完整的现象。

针对上述问题，提出了视觉传达下多聚焦图像相邻像素图层融合方法，使用高阶统计量算法对目标图像进行去噪处理，通过二维飞控无缝融合技术，对多聚焦图像相邻像素图层进行融合。实验证明该方法具有一定的优越性。

2 多聚焦图像相邻像素图层融合的实现

2.1 高阶统计量去噪

目前使用最多的多聚焦图像平滑方法为中值滤波法与加权平均法等。对于二维的多聚焦图像[4]来说，将一种活动窗口沿着图像的边缘进行移动就是中值滤波法，用窗口里所有像素灰度值的中值代替窗口中心位置的相邻像素灰度。考虑到多聚焦图像在二维方向上都包含相关性，所以，活动窗口大多使用二维窗口(5*5、6*6或8*8等)。窗口的形态常见的有十字形、圆形、X字形和正方形等。

设f(x，y)代表待处理的图像，g(x，y)代表处理后的图像，那么加权平均法图像处理的代表式能够表达为

(1)

式中，h(m，n)代表加权平均系数矩阵，A为相邻像素点中的一个区域，这种去噪方法中，h(m，n)平滑的作用越大，矩阵中心的元素值占据就越小，但是其带来的副作用也很大，比如图像模糊。同时h(m，n)的作用域越大，多聚焦图像就越模糊，平滑的效果就越强。

为了最大限度的平滑多聚焦图像的噪声[5]，并且保留细节，差值滤波算法首先设定了一个以某个点为中心的4*4的图像窗口，并把其分割成46°、157°与水平垂直4个方向上的7个4*4矩阵，经过计算矩阵对角线之间水文梯度绝对值总和，并且对比其尺寸，通过该方法来检测此点周围边缘的细节分布状态，然后在利用边缘细节中的梯度绝对值之和，利用其中最小6个点的均衡值，对此点的灰度值进行替换，就能够更好的保护多聚焦图像中的细节位置声并进行滤波多聚焦图像去噪。

此方法在滑动窗口中相邻像素的灰度排序基础上，使用任意数值替换窗口的中心像素的灰度值，但忽略了图像边缘细节中额值滤波；同样，也不同于是利用邻域内的各种像素灰度加权平均值进行替代中心像素初始的灰度值[6]，该方法虽然能够保护多聚焦图像的细节，不过同时也削弱图像对噪声平滑作用的加权平均滤波，说明起始图像中其细节信息较少的那一部分的梯度绝对值总和值，是比较小的。由于其噪声的叠加，其梯度绝对值的总和值有可能变得较大，会错误的以为，包含较多的细节信息，从而能够降低对噪声的平滑效果，并且多聚焦图像的细节也会出现较大的丢失情况。

针对上述的问题，利用高阶统计量去噪方法，是对多聚焦图像进行去噪。其具体的流程如下。

以c表示累积量，m代表矩，那么k阶矩与k阶累积量分别是k-1个单独变元的函数，记为mk(τ1，τ2，…，τk-1)与ck(τ1，τ2，…，τk-1)，称随机变量{x(n)，x(n+τ1)，…，x(n+τk-1)}的k阶联合矩与k阶累积量。各阶矩的表达公式为

m1=E[x(k)]

(2)

m2(τ1)=E[x(k)x(k+τ1)]

(3)

m3(τ1，τ2)=E[x(k)x(k+τ1)x(k+τ2)]

(4)

各阶累积量为

c1=m1=E[x(k)]

(5)

=E{[x(k)-m1][x(k+τ1)-m1]}

…

(6)

c3(τ1，τ2)

=E{[x(k)-m1][x(k+τ1)-m1][x(k+τ2)-m1]}

…

(7)

对于平稳高斯随机过程，有

ck(τ1，τ2，…，τk-1)=1

(8)

若k≥3，则通过式(7)可知，当图像中的叠加噪声是高斯噪声[7]时，三阶之上的累积量值为零，因此，在进行累积量计算时，不会受到噪声的干扰。

设尺寸为m×n的多聚焦图像为f(x，y){x=0，1，2，…，M-1;y=0，1，2，…，N-1}对某个相邻的像素点(x，y)，要先得到一个包围此点的3*3窗口，然后再把该窗口进行分割成6个3*3的重叠子窗口，接着分别计算6个子窗口的三阶累积量c31，c32，c33，c34，其中c的尺寸就应征了此子窗口内的多聚焦图像细节丰富程度，最终通过最小的子窗口中5个点来作为相邻像素值的平均值(x，y)点，这样，就能够很好的对叠加在多聚焦图像上的噪声进行消除和衰减，还可以保留较多的细节。

2.2 二维飞控相邻像素图层无缝融合

在上述多聚焦图像平滑去噪的基础上，将处理结果输入到二维飞控图层无缝融合中。通过最大子图分离方法，分离二维视景图层[8]，在基于以上的最大子图层平滑方法，融合二维视景无缝图层[9]。

通过使用最大子图层平滑的二维视景模型，可以获得较为稳态时的最大子图层平滑二维视景的无缝融合量为

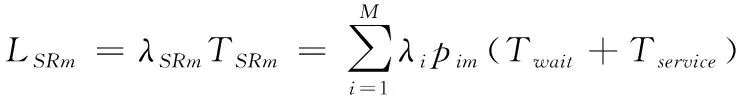
(9)

式中，LSRm代表最大子图层平滑的二维飞控视景的无缝融合量。

其总合最大子图层平滑的二维飞控视景数据利用率，进一步能够获取最大子图层平滑视景数据的处理请求量，如式(10)所示

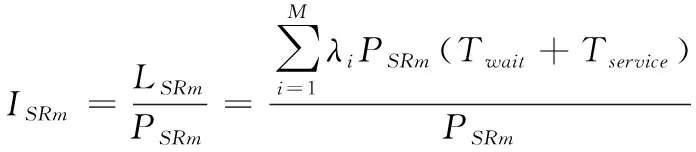
(10)

式中，ISRm代表最大子图层平滑的二维飞控视景数据处理请求量。

在获得整幅的最大子图层平滑的二维飞控视景无缝融合任务量时，同时也是该模型的另外一种融合目标，在针对偏离平滑曲线的视景仿真点上，使用序列方法将其进行矫正，计算方法如式(11)所示

(11)

将最大子图层的二维飞控视视景融合问题，进行替换成一个多目标的优化模型，寻找出最优质的分配几率pim，从而得到最小化的二维飞控视景融合响应。与此同时，依据最大子图层平滑的二维飞控视景服务，对其计算出最大化的平均无缝融合量Itotal，公式表示为

(12)

(13)

最后通过上述平滑后的图层进行组合，从而达到整幅多聚焦图像的连惯性无缝图层融合的结果。

3 融合质量的评判

融合图层的质量评测，是一种较为复杂的问题，也是相邻像素图层融合的一项重要步骤。融合图层质量测评方法通常能够分为两种：一种是主观测评法，即目视测评方法；另一种是客观测评法。

3.1 融合图层质量的主观测评法

主观测评法就是根据人眼对融合图层的质量进行主观测评的方法。比如，能够使观察者对利用不同融合方法得到的融合图层中指定目标进行识别，测量出识别时间，并计算出识别的正确率等，从而判断出图层融合方法性能的优劣与融合图层质量的好坏。主观测评法含有简单、直观的优点，对明显的图像信息能够进行方便、快捷的测评。例如在夜视系统开发计划中，研究者就是使用主观测评法来比较两种假彩色图层融合方法的优劣。因为这套系统的目的是提升飞行员夜视能力的，所以主观测评法不失为一种最优质的选择。

3.2 融合图层质量的客观评测法

融合图层质量测评离不开视觉测评。但是，图像的视觉质量主要在于观察者，含有主观性强、可重复性和片面等缺点。并且在观测条件产生变化时，测评的结果有可能出现偏差。因此，需要和客观的定量测评标准相结合进行综合测评，就是对融合图层质量在目视主观测评的基础上，进行客观定量测评。该方法使用了均值[10]、信息熵、清晰度与标准差当做质量测评参数。

1)标准差σ

设图层为Z，图层函数为Z(x，y)图层的列数与行数分别是N与M，那么图层的尺寸为M×N，L代表图层总的灰度级。图层的标准差σ定义为

(14)

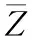
(15)

标准差映射了图层灰度对应灰度平均值的离散状态。其在一定的程度中，标准差也可以对测评图像反差的大小进行测评。如果标准差较大，所以说明图像灰度级的分布就比较分散，反差较大，能够看到更多的信息；与之相反，标准差小，图像反差小，对比度不大，色调较为均衡单一，看不到太多实用的信息。

2)信息熵E

依据Shannon信息论的原则，待评价图像的信息熵为：

(16)

式中Pl代表图层中相邻像素灰度值为l的几率。

图层的熵值代表衡量图像信息丰富程度的重要标准。根据信息论理论，如果融合的图层熵[11]越大，那么，就代表融合图层的信息量越多，信息越丰富，质量越好。

3)均值代表图像中相邻像素的灰度值，对人眼反射未平均亮度。

4)图像的清晰度

图像的清晰度[12]能够使用梯度法来衡量，图像的梯度计算公式为

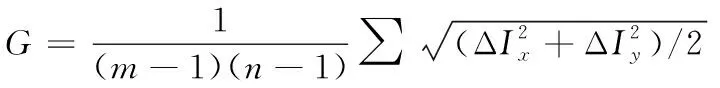
(17)

式中，ΔIx和ΔIy分别代表垂直方向和水平方向的差分，图像尺寸为m×n。如果G越大，那么图像的清晰度就会越大，比较好的融合算法能够对图像清晰度进行改善。

4 仿真研究

仿真环境为Intel Celeron Tulatin1GHz CPU和384MB SD内存的硬件环境和MATLAB6.1的软件环境。为了验证本文方法能够有效融合多聚焦图像相邻像素图层，方法具体流程见图1。

图1 本文方法融合流程图

为了进一步验证本文方法在实际应用中的性能，使用文献[1]方法、文献[2]方法和本文方法对比。图像尺寸为247*247，147级灰度值。其中多聚焦图处理结果见图2。

图2 原始图像

通过上述图像能够看出，图3(b)文献[1]方法在融合完成后，在一定程度上消减了多聚焦图像的模糊程度，但整体图像还是略微模糊。图3(c)文献[2]方法在融合完成后，清晰的体现出了多聚焦图像。但其在去噪方面还是较为不足，导致融合后的图片出现高密度斑点噪声。图3(a)为本文方法，在完成融合后，本文方法能够清晰的体现出多聚焦图像的特征，并且去噪效果非常完美。

图3 不同方法融合结果对比

分析表1可知，相较文献[1]和文献[2]方法，本文方法在进行多聚焦图像相邻像素图层融合时，针对偏离平滑曲线的视景仿真点矫正误差较低，最低误差率为0.02%，这是由于本文方法采用了序列方法，将最大子图层的二维飞控视景融合问题，替换成一个多目标的优化模型，寻找出最优质的分配几率，从而实现最小化视景矫正。

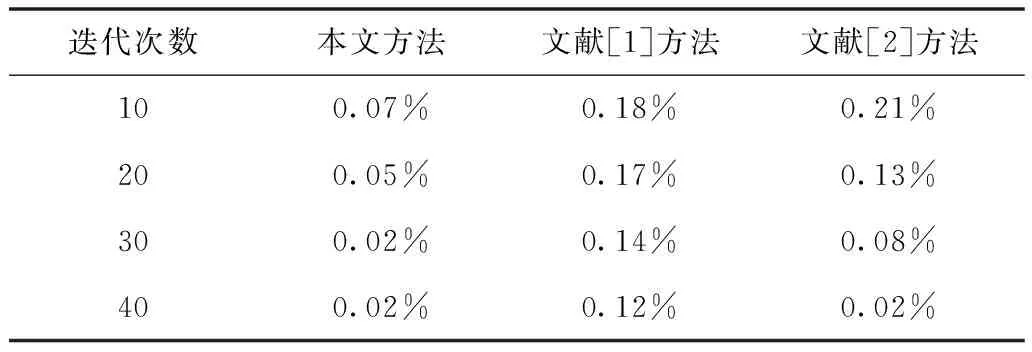
表1 偏离平滑曲线的矫正误差率(单位：%)

分析表2结果可知，本文方法的时间开销较短，平均耗时为1.12ms，最少耗时可低至0.83ms，有效提高了图像融合的实时性。这是由于本文方法通过使用最大子图层平滑的二维视景模型，无缝融合二维视景，通过无缝融合技术提高图像融合效率，减少融合时间开销。

表2 时间开销对比(单位：ms)

5 结论

针对视觉传达下多聚焦图像相邻像素图层融合中存在的融合后图像模糊、融合含有高密度斑点噪声问题，本文利用高阶统计量去噪算法和二维飞控无缝融合技术对多聚焦图像进行图层融合，首先使用高级统计量去噪算法对待处理图像进行去噪，使得在后续融合过程中不会受到高密度斑点噪声的影响，然后使用二维飞控无缝融合技术对去噪后的图层进行平滑融合。仿真证明，本文方法在融合多聚焦图像相邻像素图层方面，有着融合图像清晰且完整的优点。